12.2.3 多项式与多项式相乘 导学案(含答案)
文档属性
| 名称 | 12.2.3 多项式与多项式相乘 导学案(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 60.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-15 11:42:09 | ||
图片预览

文档简介
12.2.3多项式与多项式相乘 导学案
一、学习目标:1.记住多项式与多项式相乘的法则,并理解其推导过程;
2.能运用多项式与多项式相乘的法则进行运算;
3.能综合运用整式的有关运算法则进行整式的加、减、乘混合运算.
二 、自主学习
【情境导入】李老师做了一个长方形教具,其中一边长为2a+b,另一边长为a-b,则该长方形的面积为多少?小明与小刚对此问题陷入了深思……
知识点1 多项式与多项式相乘的法则
阅读教材第28页的内容,回答下列问题:
1.在图12.2.1中,(1)当把长方形林地看作长为(m+n)米,宽为(a+b)米时,林地的面积表示为 平方米;(2)当把长方形林地看作上下两个长方形组成时,林地的面积表示为 平方米;(3)当把长方形林地看作左右两个长方形组成时,林地的面积表示为 平方米;(4)当把长方形林地看作四小块组成时,林地的面积表示为 平方米.
由此,我们得到:(m+n)(a+b)=(m+n)a+(m+n)b= = .
2.从等式(m+n)(a+b)=ma+mb+na+nb,我们发现:结果的前两项是用m分别去 ,后两项是 .
【归纳总结】多项式与多项式相乘,先用一个多项式的 乘以另一个多项式的 ,再把所得的积 .
【巩固练习】如图,甲、乙、丙、丁四位同学给出了四种表示该长方形面积的多项式:
①(2a+b)(m+n);
②2a(m+n)+b(m+n);
③m(2a+b)+n(2a+b);
④2am+2an+bm+bn,
你认为其中正确的有( )
A.①② B.③④ C.①②③ D.①②③④
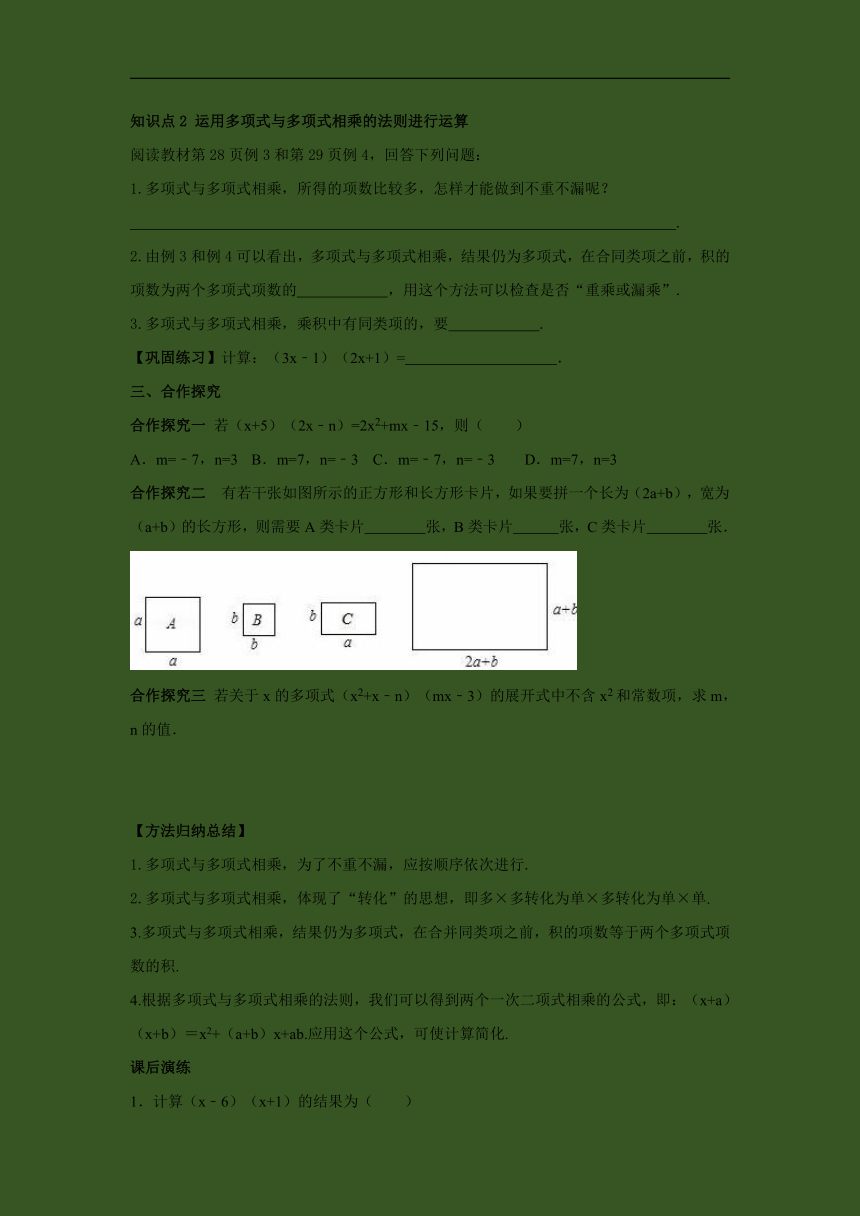
知识点2 运用多项式与多项式相乘的法则进行运算
阅读教材第28页例3和第29页例4,回答下列问题:
1.多项式与多项式相乘,所得的项数比较多,怎样才能做到不重不漏呢?
.
2.由例3和例4可以看出,多项式与多项式相乘,结果仍为多项式,在合同类项之前,积的项数为两个多项式项数的 ,用这个方法可以检查是否“重乘或漏乘”.
3.多项式与多项式相乘,乘积中有同类项的,要 .
【巩固练习】计算:(3x﹣1)(2x+1)= .
三、合作探究
合作探究一 若(x+5)(2x﹣n)=2x2+mx﹣15,则( )
A.m=﹣7,n=3 B.m=7,n=﹣3 C.m=﹣7,n=﹣3 D.m=7,n=3
合作探究二 有若干张如图所示的正方形和长方形卡片,如果要拼一个长为(2a+b),宽为(a+b)的长方形,则需要A类卡片 张,B类卡片 张,C类卡片 张.
合作探究三 若关于x的多项式(x2+x﹣n)(mx﹣3)的展开式中不含x2和常数项,求m,n的值.
【方法归纳总结】
1.多项式与多项式相乘,为了不重不漏,应按顺序依次进行.
2.多项式与多项式相乘,体现了“转化”的思想,即多×多转化为单×多转化为单×单.
3.多项式与多项式相乘,结果仍为多项式,在合并同类项之前,积的项数等于两个多项式项数的积.
4.根据多项式与多项式相乘的法则,我们可以得到两个一次二项式相乘的公式,即:(x+a)(x+b)=x2+(a+b)x+ab.应用这个公式,可使计算简化.
课后演练
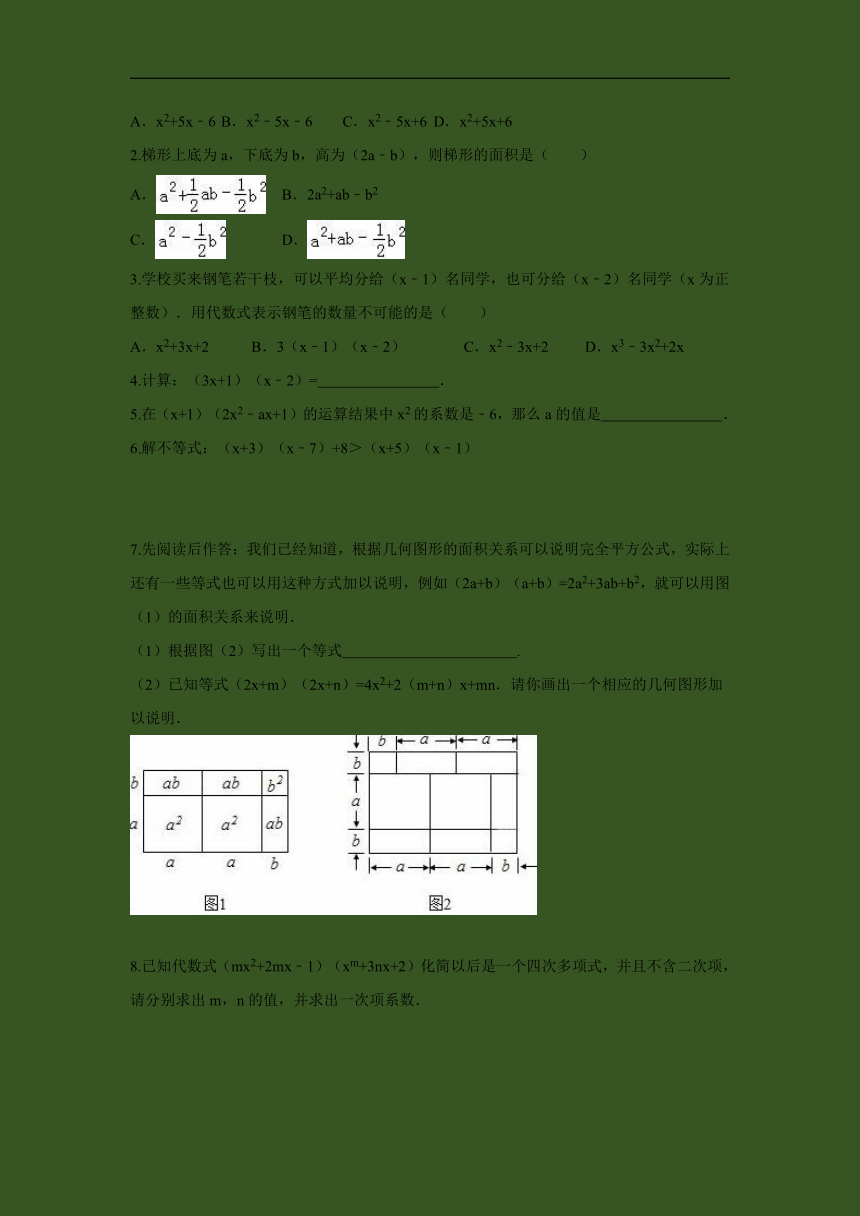
1.计算(x﹣6)(x+1)的结果为( )
A.x2+5x﹣6 B.x2﹣5x﹣6 C.x2﹣5x+6 D.x2+5x+6
2.梯形上底为a,下底为b,高为(2a﹣b),则梯形的面积是( )
A. B.2a2+ab﹣b2
C. D.
3.学校买来钢笔若干枝,可以平均分给(x﹣1)名同学,也可分给(x﹣2)名同学(x为正整数).用代数式表示钢笔的数量不可能的是( )
A.x2+3x+2 B.3(x﹣1)(x﹣2) C.x2﹣3x+2 D.x3﹣3x2+2x
4.计算:(3x+1)(x﹣2)= .
5.在(x+1)(2x2﹣ax+1)的运算结果中x2的系数是﹣6,那么a的值是 .
6.解不等式:(x+3)(x﹣7)+8>(x+5)(x﹣1)
7.先阅读后作答:我们已经知道,根据几何图形的面积关系可以说明完全平方公式,实际上还有一些等式也可以用这种方式加以说明,例如(2a+b)(a+b)=2a2+3ab+b2,就可以用图(1)的面积关系来说明.
(1)根据图(2)写出一个等式 .
(2)已知等式(2x+m)(2x+n)=4x2+2(m+n)x+mn.请你画出一个相应的几何图形加以说明.
8.已知代数式(mx2+2mx﹣1)(xm+3nx+2)化简以后是一个四次多项式,并且不含二次项,请分别求出m,n的值,并求出一次项系数.
《12.2.3多项式与多项式相乘》导学案参考答案
自主学习
知识点1
1.(1)(m+n)(a+b) (2)[(m+n)a+(m+n)b] (3)[(a+b)m+(a+b)n]
(4)(ma+mb+na+nb) (a+b)m+(a+b)n ma+mb+na+nb
2.乘以a和b 用n分别去乘以a和b
【归纳总结】每一项 每一项 相加
【巩固练习】D 解:①大长方形的长为2a+b,宽为m+n,所以长方形的面积为(2a+b)(m+n);
②长方形的面积等于左边,中间及右边的长方形面积之和,即2a(m+n)+b(m+n);
③长方形的面积等于上下两个长方形面积之和,即m(2a+b)+n(2a+b);
④长方形的面积由6个长方形的面积之和,即2am+2an+bm+bn.
所以正确的有①②③④.故选D.
知识点2
1.答:按顺序去乘,先用第一个多项式的第一项与第二个多项式的每一项依次相乘,然后再用第一个多项式的第二项与第二个多项式的每一项依次相乘,依次类推,直到第一个多项式的最后一项与第二个多项式的最后一项相乘为止
2.积
3.合并同类项
【巩固练习】6x2+x﹣1 解:(3x﹣1)(2x+1)=6x2+x﹣1.故答案为:6x2+x﹣1.
合作探究
合作探究一D 解:∵(x+5)(2x﹣n)=2x2+(10﹣n)x﹣5n,
而(x+5)(2x﹣n)=2x2+mx﹣15,
∴2x2+(10﹣n)x﹣5n=2x2+mx﹣15,
∴10﹣n=m,﹣5n=﹣15,
∴m=7,n=3.
故选D.
合作探究二2 1 3 解:长为2a+b,宽为a+b的矩形面积为(2a+b)(a+b)=2a2+3ab+b2,A图形面积为a2,B图形面积为b2,C图形面积为ab,则可知需要A类卡片2张,B类卡片1张,C类卡片3张.故答案为:2;1;3.
合作探究三解:原式=mx3+(m﹣3)x2﹣(3+mn)x+3n,
由展开式中不含x2和常数项,得到m﹣3=0,3n=0,
解得:m=3,n=0.
课后演练
1.B 解:原式=x2+x﹣6x﹣6=x2﹣5x﹣6.故选B
2.A 解:根据题意得:S=(a+b)(2a﹣b)=a2+ab﹣b2.故选A
3.A 解:根据题意得:(x﹣1)(x﹣2)=x2﹣3x+2,则钢笔的数量不可能的是x2+3x+2,故选A
4.3x2﹣5x﹣2 解:(3x+1)(x﹣2)=3x2﹣6x+x﹣2=3x2﹣5x﹣2.
5.8 解:(x+1)(2x2﹣ax+1)
=2x3﹣ax2+x+2x2﹣ax+1
=2x3+(﹣a+2)x2+(1﹣a)x+1;
∵运算结果中x2的系数是﹣6,
∴﹣a+2=﹣6,
解得a=8,
故答案为:8.
6.解:去括号得:x2﹣4x﹣21+8>x2+4x﹣5,
移项合并得:8x<﹣8,
解得:x<﹣1.
7.解:(1)根据题意得:(a+2b)(2a+b)=2a2+5ab+2b2;
(2)如图所示,
8.解:(mx2+2mx﹣1)(xm+3nx+2)=mxm+2+3mnx3+2mx2+2mxm+1+6mnx2+4mx﹣xm﹣3nx﹣2,
因为该多项式是四次多项式,
所以m+2=4,
解得:m=2,
原式=2x4+(6n+4)x3+(3+12n)x2+(8﹣3n)x﹣2
∵多项式不含二次项
∴3+12n=0,
解得:n=,
所以一次项系数8﹣3n=8.75.
一、学习目标:1.记住多项式与多项式相乘的法则,并理解其推导过程;
2.能运用多项式与多项式相乘的法则进行运算;
3.能综合运用整式的有关运算法则进行整式的加、减、乘混合运算.
二 、自主学习
【情境导入】李老师做了一个长方形教具,其中一边长为2a+b,另一边长为a-b,则该长方形的面积为多少?小明与小刚对此问题陷入了深思……
知识点1 多项式与多项式相乘的法则
阅读教材第28页的内容,回答下列问题:
1.在图12.2.1中,(1)当把长方形林地看作长为(m+n)米,宽为(a+b)米时,林地的面积表示为 平方米;(2)当把长方形林地看作上下两个长方形组成时,林地的面积表示为 平方米;(3)当把长方形林地看作左右两个长方形组成时,林地的面积表示为 平方米;(4)当把长方形林地看作四小块组成时,林地的面积表示为 平方米.
由此,我们得到:(m+n)(a+b)=(m+n)a+(m+n)b= = .
2.从等式(m+n)(a+b)=ma+mb+na+nb,我们发现:结果的前两项是用m分别去 ,后两项是 .
【归纳总结】多项式与多项式相乘,先用一个多项式的 乘以另一个多项式的 ,再把所得的积 .
【巩固练习】如图,甲、乙、丙、丁四位同学给出了四种表示该长方形面积的多项式:
①(2a+b)(m+n);
②2a(m+n)+b(m+n);
③m(2a+b)+n(2a+b);
④2am+2an+bm+bn,
你认为其中正确的有( )
A.①② B.③④ C.①②③ D.①②③④
知识点2 运用多项式与多项式相乘的法则进行运算
阅读教材第28页例3和第29页例4,回答下列问题:
1.多项式与多项式相乘,所得的项数比较多,怎样才能做到不重不漏呢?
.
2.由例3和例4可以看出,多项式与多项式相乘,结果仍为多项式,在合同类项之前,积的项数为两个多项式项数的 ,用这个方法可以检查是否“重乘或漏乘”.
3.多项式与多项式相乘,乘积中有同类项的,要 .
【巩固练习】计算:(3x﹣1)(2x+1)= .
三、合作探究
合作探究一 若(x+5)(2x﹣n)=2x2+mx﹣15,则( )
A.m=﹣7,n=3 B.m=7,n=﹣3 C.m=﹣7,n=﹣3 D.m=7,n=3
合作探究二 有若干张如图所示的正方形和长方形卡片,如果要拼一个长为(2a+b),宽为(a+b)的长方形,则需要A类卡片 张,B类卡片 张,C类卡片 张.
合作探究三 若关于x的多项式(x2+x﹣n)(mx﹣3)的展开式中不含x2和常数项,求m,n的值.
【方法归纳总结】
1.多项式与多项式相乘,为了不重不漏,应按顺序依次进行.
2.多项式与多项式相乘,体现了“转化”的思想,即多×多转化为单×多转化为单×单.
3.多项式与多项式相乘,结果仍为多项式,在合并同类项之前,积的项数等于两个多项式项数的积.
4.根据多项式与多项式相乘的法则,我们可以得到两个一次二项式相乘的公式,即:(x+a)(x+b)=x2+(a+b)x+ab.应用这个公式,可使计算简化.
课后演练
1.计算(x﹣6)(x+1)的结果为( )
A.x2+5x﹣6 B.x2﹣5x﹣6 C.x2﹣5x+6 D.x2+5x+6
2.梯形上底为a,下底为b,高为(2a﹣b),则梯形的面积是( )
A. B.2a2+ab﹣b2
C. D.
3.学校买来钢笔若干枝,可以平均分给(x﹣1)名同学,也可分给(x﹣2)名同学(x为正整数).用代数式表示钢笔的数量不可能的是( )
A.x2+3x+2 B.3(x﹣1)(x﹣2) C.x2﹣3x+2 D.x3﹣3x2+2x
4.计算:(3x+1)(x﹣2)= .
5.在(x+1)(2x2﹣ax+1)的运算结果中x2的系数是﹣6,那么a的值是 .
6.解不等式:(x+3)(x﹣7)+8>(x+5)(x﹣1)
7.先阅读后作答:我们已经知道,根据几何图形的面积关系可以说明完全平方公式,实际上还有一些等式也可以用这种方式加以说明,例如(2a+b)(a+b)=2a2+3ab+b2,就可以用图(1)的面积关系来说明.
(1)根据图(2)写出一个等式 .
(2)已知等式(2x+m)(2x+n)=4x2+2(m+n)x+mn.请你画出一个相应的几何图形加以说明.
8.已知代数式(mx2+2mx﹣1)(xm+3nx+2)化简以后是一个四次多项式,并且不含二次项,请分别求出m,n的值,并求出一次项系数.
《12.2.3多项式与多项式相乘》导学案参考答案
自主学习
知识点1
1.(1)(m+n)(a+b) (2)[(m+n)a+(m+n)b] (3)[(a+b)m+(a+b)n]
(4)(ma+mb+na+nb) (a+b)m+(a+b)n ma+mb+na+nb
2.乘以a和b 用n分别去乘以a和b
【归纳总结】每一项 每一项 相加
【巩固练习】D 解:①大长方形的长为2a+b,宽为m+n,所以长方形的面积为(2a+b)(m+n);
②长方形的面积等于左边,中间及右边的长方形面积之和,即2a(m+n)+b(m+n);
③长方形的面积等于上下两个长方形面积之和,即m(2a+b)+n(2a+b);
④长方形的面积由6个长方形的面积之和,即2am+2an+bm+bn.
所以正确的有①②③④.故选D.
知识点2
1.答:按顺序去乘,先用第一个多项式的第一项与第二个多项式的每一项依次相乘,然后再用第一个多项式的第二项与第二个多项式的每一项依次相乘,依次类推,直到第一个多项式的最后一项与第二个多项式的最后一项相乘为止
2.积
3.合并同类项
【巩固练习】6x2+x﹣1 解:(3x﹣1)(2x+1)=6x2+x﹣1.故答案为:6x2+x﹣1.
合作探究
合作探究一D 解:∵(x+5)(2x﹣n)=2x2+(10﹣n)x﹣5n,
而(x+5)(2x﹣n)=2x2+mx﹣15,
∴2x2+(10﹣n)x﹣5n=2x2+mx﹣15,
∴10﹣n=m,﹣5n=﹣15,
∴m=7,n=3.
故选D.
合作探究二2 1 3 解:长为2a+b,宽为a+b的矩形面积为(2a+b)(a+b)=2a2+3ab+b2,A图形面积为a2,B图形面积为b2,C图形面积为ab,则可知需要A类卡片2张,B类卡片1张,C类卡片3张.故答案为:2;1;3.
合作探究三解:原式=mx3+(m﹣3)x2﹣(3+mn)x+3n,
由展开式中不含x2和常数项,得到m﹣3=0,3n=0,
解得:m=3,n=0.
课后演练
1.B 解:原式=x2+x﹣6x﹣6=x2﹣5x﹣6.故选B
2.A 解:根据题意得:S=(a+b)(2a﹣b)=a2+ab﹣b2.故选A
3.A 解:根据题意得:(x﹣1)(x﹣2)=x2﹣3x+2,则钢笔的数量不可能的是x2+3x+2,故选A
4.3x2﹣5x﹣2 解:(3x+1)(x﹣2)=3x2﹣6x+x﹣2=3x2﹣5x﹣2.
5.8 解:(x+1)(2x2﹣ax+1)
=2x3﹣ax2+x+2x2﹣ax+1
=2x3+(﹣a+2)x2+(1﹣a)x+1;
∵运算结果中x2的系数是﹣6,
∴﹣a+2=﹣6,
解得a=8,
故答案为:8.
6.解:去括号得:x2﹣4x﹣21+8>x2+4x﹣5,
移项合并得:8x<﹣8,
解得:x<﹣1.
7.解:(1)根据题意得:(a+2b)(2a+b)=2a2+5ab+2b2;
(2)如图所示,
8.解:(mx2+2mx﹣1)(xm+3nx+2)=mxm+2+3mnx3+2mx2+2mxm+1+6mnx2+4mx﹣xm﹣3nx﹣2,
因为该多项式是四次多项式,
所以m+2=4,
解得:m=2,
原式=2x4+(6n+4)x3+(3+12n)x2+(8﹣3n)x﹣2
∵多项式不含二次项
∴3+12n=0,
解得:n=,
所以一次项系数8﹣3n=8.75.
