13.5.2 线段垂直平分线 课件(34张PPT)
文档属性
| 名称 | 13.5.2 线段垂直平分线 课件(34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 857.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-15 00:00:00 | ||
图片预览










文档简介
课件34张PPT。第13章 全等三角形13.5 逆命题与逆定理线段的垂直平分线线段垂直平分线的性质
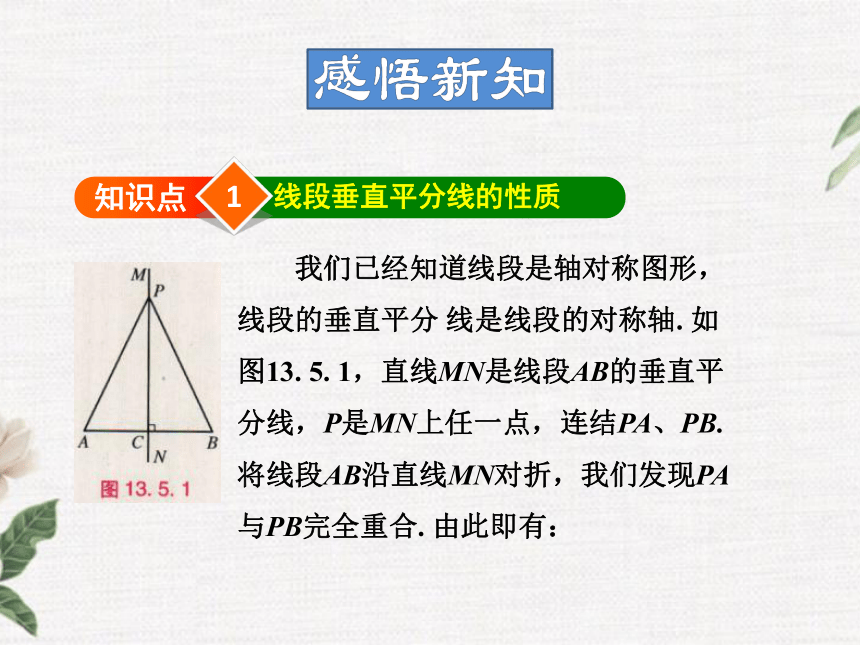
线段垂直平分线的判定1知识点线段垂直平分线的性质 我们已经知道线段是轴对称图形,
线段的垂直平分 线是线段的对称轴. 如
图13. 5. 1,直线MN是线段AB的垂直平
分线,P是MN上任一点,连结PA、PB.
将线段AB沿直线MN对折,我们发现PA
与PB完全重合. 由此即有:1.线段垂直平分线的性质定理:线段垂
直平分线上的点到线段两端的距离相等;
条件:点在线段的垂直平分线上;
结论:这个点到线段两端的距离相等.
表达方式:如图13.5--2,l ⊥ AB,AO
=BO,点P在l上,则AP=BP.
2.作用:可用来证明两线段相等.
图13.5--2线段垂直平分线的性质定理线段垂
直平分线上 的点到线段两端的距离相等.
已知:如图13. 5. 1,MN丄AB,垂
足为点C,AC =BC,点P是直线MN上的
任意一点.
求证:PA=PB.
分析:图中有两个直角三角形APC
和BPC,只要 证明这两个三角形全等,
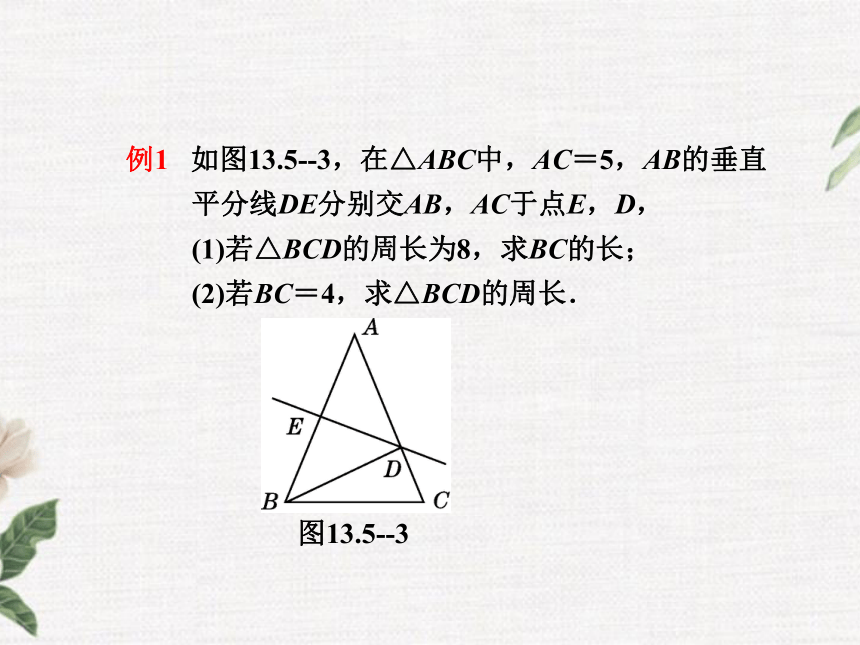
便可证得PA=PB.请写出完整的证明过程. 例1 如图13.5--3,在△ABC中,AC=5,AB的垂直平分线DE分别交AB,AC于点E,D,
(1)若△BCD的周长为8,求BC的长;
(2)若BC=4,求△BCD的周长.图13.5--3导引:由DE是AB的垂直平分线,得AD=BD,所以
BD与CD的长度和等于AC的长,所以由△BCD
的周长可求BC的长,同样由BC的长也可求
△BCD的周长.解:∵DE是AB的垂直平分线,∴AD=BD,
∴BD+CD=AD+CD=AC=5.
(1)∵△BCD的周长为8,
∴BC=△BCD的周长-(BD+CD)=8-5=3.
(2)∵BC=4,
∴△BCD的周长=BC+BD+CD=5+4=9.?总 结本题运用了转化思想,用线段垂直平分线的性
质把BD的长转化成AD的长,从而把未知的BD与CD
的长度和转化成已知的线段AC的长.本题中AC的长、
BC的长及△BCD的周长三者可互相转化,知其二可
求第三者. 例2 如图13.5--4,在△ABC中,∠A=40°,∠B=90°,线段AC的垂直平分线MN与AB交于点D,与AC交于点E,则∠BCD的度数是______.图13.5--410°导引:在△ABC中,∵∠B=90°,∠A=40°,
∴∠ACB=50°.
∵MN是线段AC的垂直平分线,
∴DC=DA,AE=CE.
又∵DE=DE,∴△ADE≌△CDE,
∴∠DCE=∠A=40°.
∴∠BCD=∠ACB-∠DCA=50°-40°=10°.总 结 利用线段垂直平分线的性质得出边相等,从而
得出三角形全等,再利用全等三角形中对应角相等
确定∠DCA的度数,根据角度差解决问题.(中考·义乌)如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点,已知线段PA=5,则线段PB的长度为( )
A.6
B.5
C.4
D.3
?2 如图,已知线段AB,BC的垂直平分线l1,l2交于点M,则线段AM,CM的大小关系是( )
A.AM>CM
B.AM=CM
C.AMD.无法确定3 (中考·荆州)如图,在△ABC中,AB=AC,AB的垂直平分线交边AB于D点,交边AC于E点,若△ABC与△EBC的周长分别是40 cm,24 cm,则AB=________.
2知识点线段垂直平分线的判定这一定理描述了线段垂直平分线的性质,那么反过 来会有
什么结果呢?探索写出该定 理与它的逆命 题的条件和结 论,想想看,其 逆命题是否是 一个真命题? 你一定发现到线段两端距离相等的点的确在该线 段的垂直
平分线上.我们可以通过“证明”说明这一结论正确.线段垂直平分线的判定定理:到线段两端距离相等的点
在线段的垂直平分线上.
(1)条件:点到线段两端距离相等;结论:
点在线段垂直平分线上.
(2)表达方式:如图13.5--5,∵PA=PB,
∴点P在线段AB的垂直平分线上.
(3)作用:①作线段的垂直平分线的依据;
②可用来证线段垂直、相等.
拓展:三角形三边的垂直平分线交于一点,这点到三角
形的三个顶点的距离相等,这个点叫这个三角形的外心.图13.5--5已知:如图13.5.2, QA=QB. 求证:点Q在线段AB的垂直平分线上.
分析:为了证明点Q在线段AB的垂
直平分线上, 可以先经过点
Q作线段AB的垂线,然后证
明该垂线平 分线段AB;也可
以先平分线段AB ,设线段AB
的中点为 点C,然后证明QC垂直于线段AB.证明:过点Q作MN丄AB ,垂足为点C,
故∠QCA = ∠QCB = 90°.
在 Rt △QCA 和 Rt △QCB 中,
∵ QA = QB, QC = QC,
Rt △QCA ≌Rt △QCB (H.L ).
∴ AC =BC (全等三角形的对应边相等).
∴点Q在线段AB的垂直平分线上.你能根据分析中后一种添加辅助 线的方法,写出它的证明过程吗?于是就有定理:
到线段两端距离相等的点在线段的垂直平分 线上.
上述两条定理互为逆定理,根据上述两条定理,
我们就能证明:三角形三边的垂直平分线交于一点. 例2 如图13.5--6,在△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E.求证:直线AD是CE的垂直平分线.
证明:∵AD平分∠BAC,
∴∠DAE=∠DAC.
∵∠ACB=90°,DE⊥AB,
∴∠AED=90°,
易证△ADE≌△ADC,∴CD=DE,
∴点D在CE的垂直平分线上;
AC=AE,∴点A也在CE的垂直平分线上,
∴直线AD是CE的垂直平分线.?图13.5--6总 结利用判定定理要证一条直线是线段的垂直平分线,
必须证明这条直线上有两点到线段两端点的距离相等
(即证有两点在线段的垂直平分线上).易错之处:只证
明一个点在线段的垂直平分线上,就说过该点的直线是
线段的垂直平分线.因为过该点的直线有无穷多条,其
中只有一条是线段的垂直平分线.注意:证线段的垂直
平分线也可以利用定义.从图13. 5. 3中可以看出,要证明三角
形三条边的垂 直平分线交于一点,只需证
明其中两条边的垂直平分线 的交点一定在
第三条边的垂直平分线上就可以了.其思 路
可表示如下:
试试看,现在你会证明了吗?
(此讲解来源于教材)试一试 例3 如图13.5--7,已知AB=AD,BC=DC,E是AC上一点,求证:(1)BE=DE;(2)∠ABE=∠ADE.
导引:(1)连结BD,要证BE=DE,只要证明E点
是线段BD的垂直平分线上的点即可.由
AB=AD,说明A点是线段BD的垂直平分
线上的点,由BC=DC,说明C点也是线
段BD的垂直平分线上的点,所以AC是线
段BD的垂直平分线,而已知E是AC上一
点,问题得以解决.
(2)要证明角相等,只需证明△ABE≌△ADE即可.图13.5--7证明:(1)连结BD,如图13.5-7,
∵AB=AD,BC=CD,
∴A,C两点均在线段BD的垂直平分线上.
∴AC是线段BD的垂直平分线.
又∵E是AC上一点,
∴BE=DE.
(2)在△ABE和△ADE中,
∵AB=AD,BE=DE,AE=AE,
∴△ABE≌△ADE,
∴∠ABE=∠ADE.总 结由线段垂直平分线的判定定理确定AC是线段BD的
垂直平分线,再由线段垂直平分线的性质得BE=DE,
这是线段垂直平分线的性质和判定定理的综合运用. 例4 如图13.5--8,某城市规划局为了方便居民的生活,计划在三个住宅小区A,B,C之间修建一个购物中心,试问:该购物中心应建于何处,才能使得它到三个小区的距离相等?图13.5-8导引:本题转化为数学问题就是要找一个点,使它到
三角形的三个顶点的距离相等.首先考虑到A,
B两点距离相等的点应该在线段AB的垂直平分
线上,到B,C两点距离相等的点应该在线段BC
的垂直平分线上,两条垂直平分线的交点即为
所求的点.图13.5--9解:连结AB,BC,分别作AB,BC的垂直平分线DE,
GF,两直线交于点M,则点M就是所要确定的购
物中心的位置.如图13.5--9.
图13.5--9总 结解决作图选点性问题:若要找到某两个点的距离
相等的点,一般在这两点所连线段的垂直平分线上去
找.总 结线段垂直平分线的判定有两种方法:(1)定义法;
(2)判定定理.我们一般习惯用定义法进行证明,但利用
判定定理则更为简单,用判定定理判定一条直线是线段
的垂直平分线时,需证直线上有两点到线段两端点的距
离相等.锐角三角形ABC内有一点P,满足PA=PB=PC,则点P是△ABC( )
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三边垂直平分线的交点2 如图,点D在△ABC的BC边上,且BC=BD+AD,则点D在线段( )的垂直平分线上.
A.AB
B.AC
C.BC
D.不确定1.线段的垂直平分线的性质和判定的“两点作用”:
(1)利用线段垂直平分线的性质可证明两线段相
等,只需直线满足垂直、平分即可;(2)利用线段垂
直平分线的判定可证明垂直关系和线段相等关系.
2.应用线段垂直平分线的性质要注意两点:
(1)点一定在垂直平分线上;(2)距离指的是点到
线段两个端点的距离.
线段垂直平分线的判定1知识点线段垂直平分线的性质 我们已经知道线段是轴对称图形,
线段的垂直平分 线是线段的对称轴. 如
图13. 5. 1,直线MN是线段AB的垂直平
分线,P是MN上任一点,连结PA、PB.
将线段AB沿直线MN对折,我们发现PA
与PB完全重合. 由此即有:1.线段垂直平分线的性质定理:线段垂
直平分线上的点到线段两端的距离相等;
条件:点在线段的垂直平分线上;
结论:这个点到线段两端的距离相等.
表达方式:如图13.5--2,l ⊥ AB,AO
=BO,点P在l上,则AP=BP.
2.作用:可用来证明两线段相等.
图13.5--2线段垂直平分线的性质定理线段垂
直平分线上 的点到线段两端的距离相等.
已知:如图13. 5. 1,MN丄AB,垂
足为点C,AC =BC,点P是直线MN上的
任意一点.
求证:PA=PB.
分析:图中有两个直角三角形APC
和BPC,只要 证明这两个三角形全等,
便可证得PA=PB.请写出完整的证明过程. 例1 如图13.5--3,在△ABC中,AC=5,AB的垂直平分线DE分别交AB,AC于点E,D,
(1)若△BCD的周长为8,求BC的长;
(2)若BC=4,求△BCD的周长.图13.5--3导引:由DE是AB的垂直平分线,得AD=BD,所以
BD与CD的长度和等于AC的长,所以由△BCD
的周长可求BC的长,同样由BC的长也可求
△BCD的周长.解:∵DE是AB的垂直平分线,∴AD=BD,
∴BD+CD=AD+CD=AC=5.
(1)∵△BCD的周长为8,
∴BC=△BCD的周长-(BD+CD)=8-5=3.
(2)∵BC=4,
∴△BCD的周长=BC+BD+CD=5+4=9.?总 结本题运用了转化思想,用线段垂直平分线的性
质把BD的长转化成AD的长,从而把未知的BD与CD
的长度和转化成已知的线段AC的长.本题中AC的长、
BC的长及△BCD的周长三者可互相转化,知其二可
求第三者. 例2 如图13.5--4,在△ABC中,∠A=40°,∠B=90°,线段AC的垂直平分线MN与AB交于点D,与AC交于点E,则∠BCD的度数是______.图13.5--410°导引:在△ABC中,∵∠B=90°,∠A=40°,
∴∠ACB=50°.
∵MN是线段AC的垂直平分线,
∴DC=DA,AE=CE.
又∵DE=DE,∴△ADE≌△CDE,
∴∠DCE=∠A=40°.
∴∠BCD=∠ACB-∠DCA=50°-40°=10°.总 结 利用线段垂直平分线的性质得出边相等,从而
得出三角形全等,再利用全等三角形中对应角相等
确定∠DCA的度数,根据角度差解决问题.(中考·义乌)如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点,已知线段PA=5,则线段PB的长度为( )
A.6
B.5
C.4
D.3
?2 如图,已知线段AB,BC的垂直平分线l1,l2交于点M,则线段AM,CM的大小关系是( )
A.AM>CM
B.AM=CM
C.AM
2知识点线段垂直平分线的判定这一定理描述了线段垂直平分线的性质,那么反过 来会有
什么结果呢?探索写出该定 理与它的逆命 题的条件和结 论,想想看,其 逆命题是否是 一个真命题? 你一定发现到线段两端距离相等的点的确在该线 段的垂直
平分线上.我们可以通过“证明”说明这一结论正确.线段垂直平分线的判定定理:到线段两端距离相等的点
在线段的垂直平分线上.
(1)条件:点到线段两端距离相等;结论:
点在线段垂直平分线上.
(2)表达方式:如图13.5--5,∵PA=PB,
∴点P在线段AB的垂直平分线上.
(3)作用:①作线段的垂直平分线的依据;
②可用来证线段垂直、相等.
拓展:三角形三边的垂直平分线交于一点,这点到三角
形的三个顶点的距离相等,这个点叫这个三角形的外心.图13.5--5已知:如图13.5.2, QA=QB. 求证:点Q在线段AB的垂直平分线上.
分析:为了证明点Q在线段AB的垂
直平分线上, 可以先经过点
Q作线段AB的垂线,然后证
明该垂线平 分线段AB;也可
以先平分线段AB ,设线段AB
的中点为 点C,然后证明QC垂直于线段AB.证明:过点Q作MN丄AB ,垂足为点C,
故∠QCA = ∠QCB = 90°.
在 Rt △QCA 和 Rt △QCB 中,
∵ QA = QB, QC = QC,
Rt △QCA ≌Rt △QCB (H.L ).
∴ AC =BC (全等三角形的对应边相等).
∴点Q在线段AB的垂直平分线上.你能根据分析中后一种添加辅助 线的方法,写出它的证明过程吗?于是就有定理:
到线段两端距离相等的点在线段的垂直平分 线上.
上述两条定理互为逆定理,根据上述两条定理,
我们就能证明:三角形三边的垂直平分线交于一点. 例2 如图13.5--6,在△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E.求证:直线AD是CE的垂直平分线.
证明:∵AD平分∠BAC,
∴∠DAE=∠DAC.
∵∠ACB=90°,DE⊥AB,
∴∠AED=90°,
易证△ADE≌△ADC,∴CD=DE,
∴点D在CE的垂直平分线上;
AC=AE,∴点A也在CE的垂直平分线上,
∴直线AD是CE的垂直平分线.?图13.5--6总 结利用判定定理要证一条直线是线段的垂直平分线,
必须证明这条直线上有两点到线段两端点的距离相等
(即证有两点在线段的垂直平分线上).易错之处:只证
明一个点在线段的垂直平分线上,就说过该点的直线是
线段的垂直平分线.因为过该点的直线有无穷多条,其
中只有一条是线段的垂直平分线.注意:证线段的垂直
平分线也可以利用定义.从图13. 5. 3中可以看出,要证明三角
形三条边的垂 直平分线交于一点,只需证
明其中两条边的垂直平分线 的交点一定在
第三条边的垂直平分线上就可以了.其思 路
可表示如下:
试试看,现在你会证明了吗?
(此讲解来源于教材)试一试 例3 如图13.5--7,已知AB=AD,BC=DC,E是AC上一点,求证:(1)BE=DE;(2)∠ABE=∠ADE.
导引:(1)连结BD,要证BE=DE,只要证明E点
是线段BD的垂直平分线上的点即可.由
AB=AD,说明A点是线段BD的垂直平分
线上的点,由BC=DC,说明C点也是线
段BD的垂直平分线上的点,所以AC是线
段BD的垂直平分线,而已知E是AC上一
点,问题得以解决.
(2)要证明角相等,只需证明△ABE≌△ADE即可.图13.5--7证明:(1)连结BD,如图13.5-7,
∵AB=AD,BC=CD,
∴A,C两点均在线段BD的垂直平分线上.
∴AC是线段BD的垂直平分线.
又∵E是AC上一点,
∴BE=DE.
(2)在△ABE和△ADE中,
∵AB=AD,BE=DE,AE=AE,
∴△ABE≌△ADE,
∴∠ABE=∠ADE.总 结由线段垂直平分线的判定定理确定AC是线段BD的
垂直平分线,再由线段垂直平分线的性质得BE=DE,
这是线段垂直平分线的性质和判定定理的综合运用. 例4 如图13.5--8,某城市规划局为了方便居民的生活,计划在三个住宅小区A,B,C之间修建一个购物中心,试问:该购物中心应建于何处,才能使得它到三个小区的距离相等?图13.5-8导引:本题转化为数学问题就是要找一个点,使它到
三角形的三个顶点的距离相等.首先考虑到A,
B两点距离相等的点应该在线段AB的垂直平分
线上,到B,C两点距离相等的点应该在线段BC
的垂直平分线上,两条垂直平分线的交点即为
所求的点.图13.5--9解:连结AB,BC,分别作AB,BC的垂直平分线DE,
GF,两直线交于点M,则点M就是所要确定的购
物中心的位置.如图13.5--9.
图13.5--9总 结解决作图选点性问题:若要找到某两个点的距离
相等的点,一般在这两点所连线段的垂直平分线上去
找.总 结线段垂直平分线的判定有两种方法:(1)定义法;
(2)判定定理.我们一般习惯用定义法进行证明,但利用
判定定理则更为简单,用判定定理判定一条直线是线段
的垂直平分线时,需证直线上有两点到线段两端点的距
离相等.锐角三角形ABC内有一点P,满足PA=PB=PC,则点P是△ABC( )
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三边垂直平分线的交点2 如图,点D在△ABC的BC边上,且BC=BD+AD,则点D在线段( )的垂直平分线上.
A.AB
B.AC
C.BC
D.不确定1.线段的垂直平分线的性质和判定的“两点作用”:
(1)利用线段垂直平分线的性质可证明两线段相
等,只需直线满足垂直、平分即可;(2)利用线段垂
直平分线的判定可证明垂直关系和线段相等关系.
2.应用线段垂直平分线的性质要注意两点:
(1)点一定在垂直平分线上;(2)距离指的是点到
线段两个端点的距离.
