13.2.4 角边角 课件(31张PPT)
文档属性
| 名称 | 13.2.4 角边角 课件(31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-15 00:00:00 | ||
图片预览







文档简介
课件31张PPT。13.2 三角形全等的判定角边角判定两三角形全等的基本事实:角边角
判定两三角形全等的定理:角角边1知识点判定两三角形全等的基本事实:角边角前面我们已经讨论,当两个三角形有两边一角对应
相等时,这两个三角形是否全等的两种情况,得到了全
等 三角形的一种判定方法.
现在,我们讨论两角一边的情况:如果两个三角形
有两个角、一条边分别对应相等,那么这两个三角形全
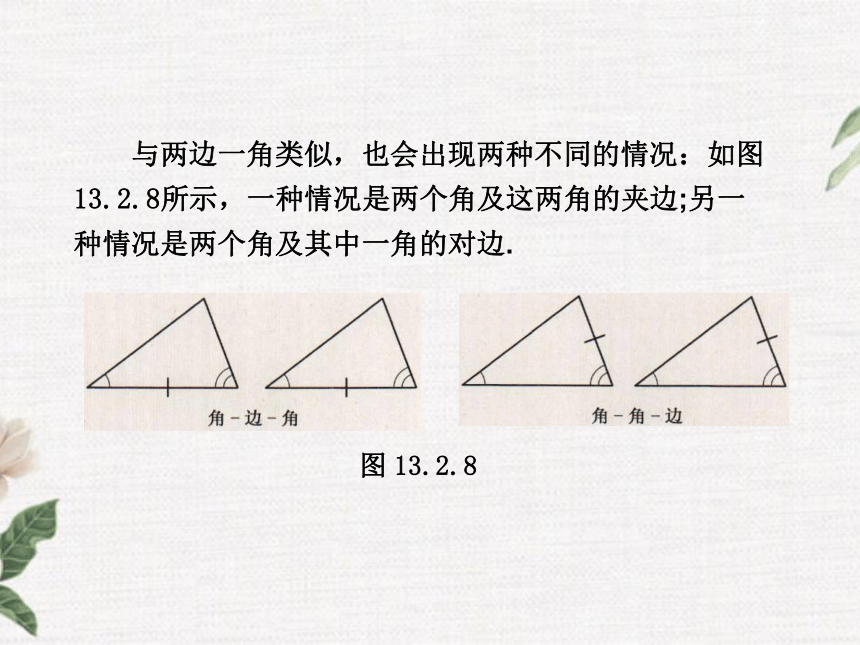
等吗?与两边一角类似,也会出现两种不同的情况:如图
13.2.8所示,一种情况是两个角及这两角的夹边;另一
种情况是两个角及其中一角的对边.
图 13.2.8 如图13.2.9,已知两个角和一条线段,试画一个三角形,
使这两个角 为其内角,这条线段为这两个角的夹边.
图 13.2.9
把你画的三角形与其他同学画
的三角形 进行比较,或将你画的三做一做步骤:
1.画一条线段AB,
使它等于3 cm;
2.画∠MAB=60°,
∠NBA=40°,MA与NB
交于点C.
△ABC即为所求.
角形剪下,放到其他 同学画的三角形上,看看是
否完全重合.所画 的三角形都全等吗?
换两个角和一条线段,试试看,是否有同样的
结论.
角边角
1.基本事实:两角及其夹边分别相等的两个三角形全
等,简记为A.S.A.(或角边角)
2. 证明书写格式:在△ABC和△A′B′C′中,
∵
∴△ABC≌△A′B′C′.
要点精析:(1)全等的元素:两角及两角夹边;(2)在书
写两个三角形全等的条件角边角时,一定要把夹边相等写
在中间,以突出角边角的位置以及对应关系.
∠A=∠A′,
AB=A′B′,
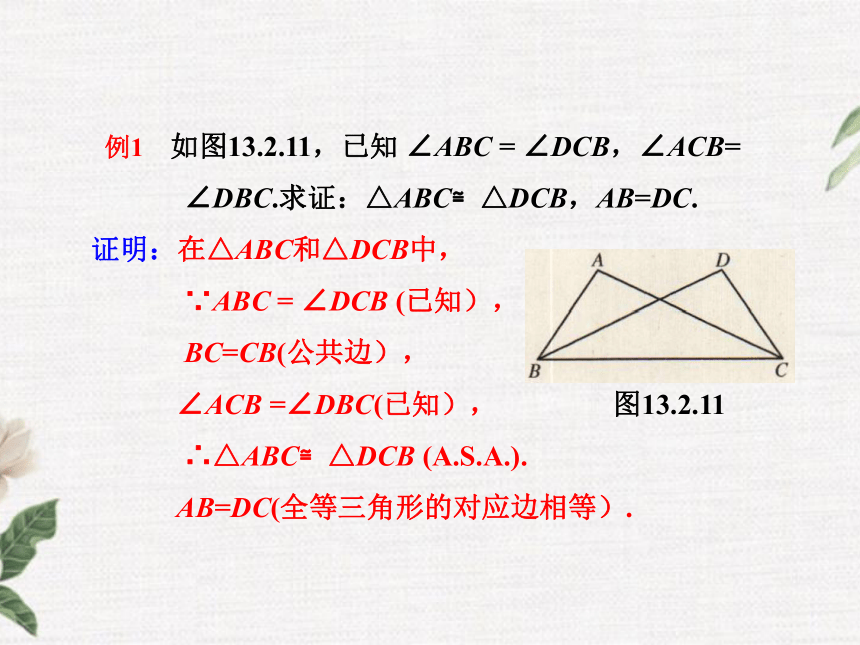
∠B=∠B′, 例1 如图13.2.11,已知 ∠ABC = ∠DCB,∠ACB=
∠DBC.求证:△ABC≌△DCB,AB=DC.
证明:在△ABC和△DCB中,
∵ABC = ∠DCB (已知),
BC=CB(公共边),
∠ACB =∠DBC(已知), 图13.2.11
∴△ABC≌△DCB (A.S.A.).
AB=DC(全等三角形的对应边相等).(1)在证两三角形全等所需要的角相等时,通常
采用的目前所学过的方法有:(1)公共角、对顶角分
别相等;(2)等角加(减)等角,其和(差)仍相等,即
等式的性质;(3)同角或等角的余(补)角相等;(4)角
平分线得到相等角;(5)平行线的同位角、内错角相
等;(6)直角都相等;(7)全等三角形对应角相等;
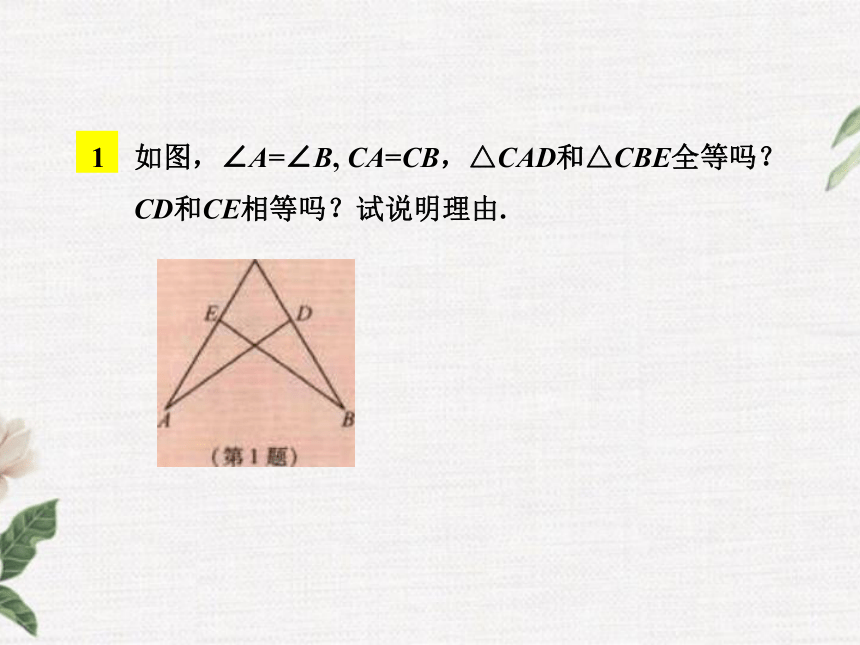
(8)第三角代换,即等量代换等.1 如图,∠A=∠B, CA=CB,△CAD和△CBE全等吗? CD和CE相等吗?试说明理由.
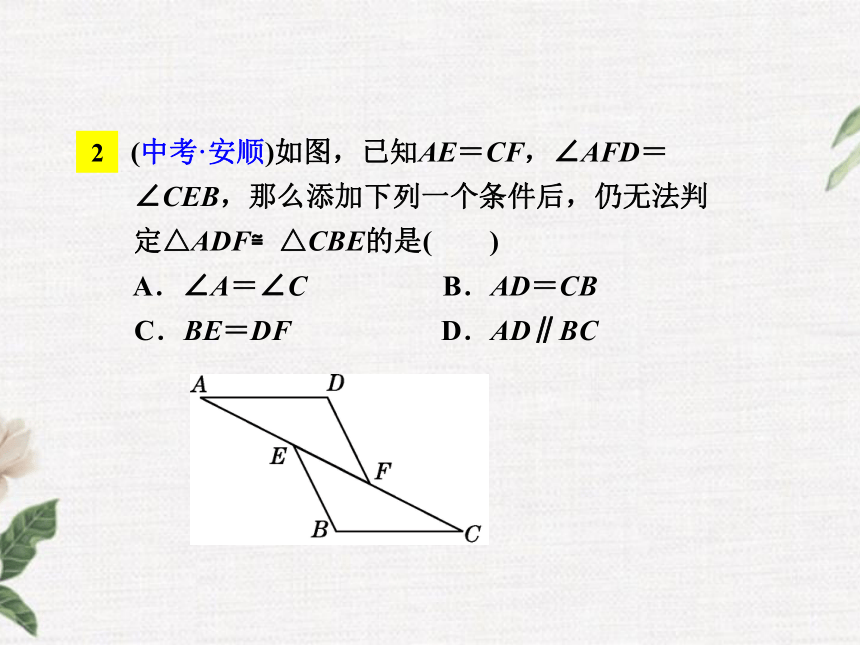
2 (中考·安顺)如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )
A.∠A=∠C B.AD=CB
C.BE=DF D.AD∥BC
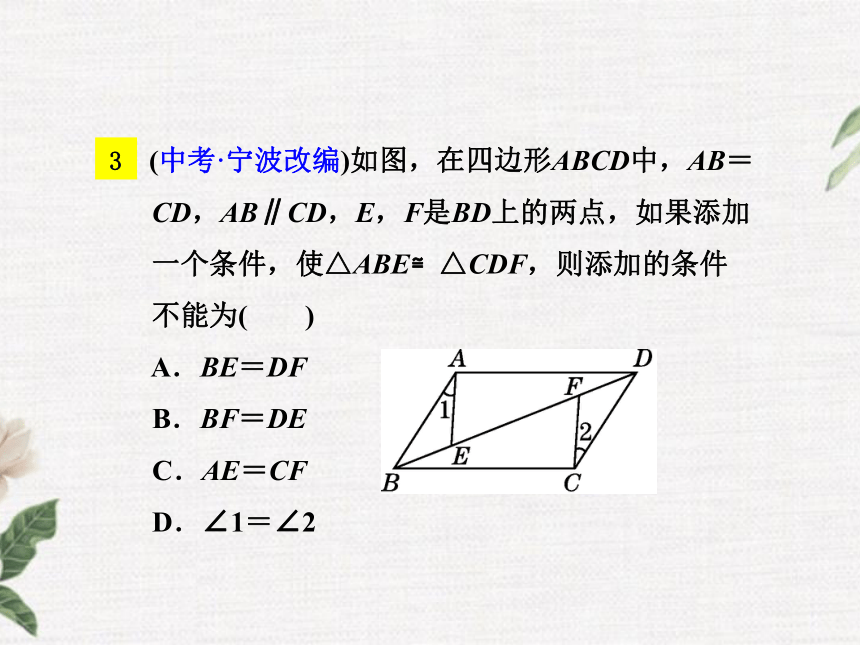
3 (中考·宁波改编)如图,在四边形ABCD中,AB=CD,AB∥CD,E,F是BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )
A.BE=DF
B.BF=DE
C.AE=CF
D.∠1=∠22知识点判定两三角形全等的定理:角角边
如图13.2. 12,如果两个三角形有
两个角分别对应 相等,且其中一组
相等的角的对边相等,那么这两个
三角 形是否一定全等?
分析:因为三角形的内角和等
于180°,因此有两个 角分别对应思考相等,那么第三个角必定对应相等,于是由 “角边
角”,便可证得这两个三角形全等.
1.定理:两角分别相等且其中一角的对边相等的两个
三角形全等,简记为A.A.S.(或角角边)
证明书写格式:在△ABC和△A′B′C′中,
∵
∴△ABC≌△A′B′C′.
要点精析:(1)全等的元素:两角及其中一角的对边;
(2)用S.A.S. ,A.S.A. ,A.A.S. 证明全等时,要注意图
形中隐含的相等的角.例如:对顶角、公共角、同角的余∠A=∠A′,
∠B=∠B′,
BC=B′C′,角(补角)都是相等的,虽然已知条件无涉及,但证明中
要特别注意挖掘这些重要条件.
(3)常见的全等三角形类型如图13.2--19所示.
图13.2--19
2.已知两角和一边对应相等就可判定两三角形全
等,即“A.S.A.或A.A.S.”
下面我们证明这个定理:
两角分别相等且其中一组等角的对边相等的两个
三角形全等.简记为A. A. S.(或角角边).
已知:如图13. 2. 12, ∠A= ∠A′, ∠B= ∠B′ ,
BC = B′C′ .
求证: △ABC≌△A′B′C′ 证明:∵ ∠A= ∠A′, ∠B= ∠B′ ,(已知),
∠A ′ +∠B ′ + ∠C ′ = 180 ° (三角形的内角和等于
180°),
∴ ∠A +∠B + ∠C ′ = 180 ° (等量代换).
又 ∵ ∠A +∠B + ∠C = 180 °(三角形的内角和等 于
180 °),
∴ ∠C= ∠C′ (等式的性质).
在△ABC 和A′B′C′中,
,
,
,
. 请补充完整证明过程. 例2 如图13.2.13,在△ABC中,D是边BC的中 点, 过点C 画直线CE, 使CE//AB, 交AD的延长线于点 E. 求证AD=ED.
证明:∵ CE//AB(已知),
∴ ∠ ABD = ∠ECD,∠BAD= ∠ CED(两直线
平行,内错角相等).
在△ ABD与△ ECD中,
∵
∴ △ ABD≌△ ECD (A.A.S.),
∴ AD= ED (全等三角形的对应边相等)
∠ ABD = ∠ECD,
∠BAD= ∠ CED(已证),
BD = CD(已知),要证明两条线段AD、ED相等,我们
发现它们分别 属于△ ABD与△ ECD ,
若能证明这两个三角形全等,便可 利
用全等三角形的对应边相等得到要证
明的结论.这就 是通常证明两条线段相
等的一个重要方法.
可以采用类似的方法证明两个角相等. 例3 求证:全等三角形对应边上的高相等.
已知:如图 13.2.14,
△ABC≌△A′B′C′ ,AD、A′D′分别是
△ABC的BC边和△A′B′C′的B′C′边上的
高.求证: AD = A′D′.
你发现AD、
A ′ D ′分别是哪两个三角形的边?这两个三角形全等吗?分析:从图13.2.14中可以看出,AD、 A′D分别属
于△ABD与△A′B′D′ ,要证AD = A′D′,只需
证明这两个三角形全等即可.
证明: ∵ △ABC≌△A′B′C′ (已知),
∴ AB=A′B′(全等三角形的对应边相等),
∵∠ B= ∠B′ (全等三角形的对应角相等).
在△ABD和△A′B′D′中,
∵
∴ △ABD≌△A′B′D′(A.A.S)
∴AD = A′D′ (全等三角形的对应边相等).
∠ ADB= ∠A ′D′ B′ = 90 °(已知),
∠ B= ∠B′ (已证),
AB=A′B′(已证), 判定两三角形全等,先根据已知条件或求证的结论
确定三角形,然后再根据三角形全等的判定方法看缺什
么条件,再去证什么条件,简言之:即综合利用分析法
和综合法寻找证明途径.
全等三角形对应边上的中线、对应角的平分线
又有 什么关系呢?你能说明其中的道理吗?思考 全等三角形除了对应边相等、对应角相等外,
还有以下几条性质:
(1)全等三角形的周长相等,面积相等;
(2)全等三角形的对应边上的中线相等、对应
边上的高线相等、对应角的角平分线相等.1 如图, ∠ 1= ∠2, ∠ C= ∠D. 求证:AC=AD.2 (中考·六盘水)如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
A.∠A=∠D
B.AB=DC
C.∠ACB=∠DBC
D.AC=BD3 (中考·通辽)如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE.求证:△ABC与△DEC全等.
证明三角形全等的“三类条件”:
直接条件:即已知中直接给出的三角形的对应边或
对应角.
隐含条件:即已知没有给出,但通过读图得到的条
件,如公共边、公共角、对顶角.
间接条件:即已知中所给条件不是三角形的对应边
和对应角,需要进一步推理.
判定两三角形全等的定理:角角边1知识点判定两三角形全等的基本事实:角边角前面我们已经讨论,当两个三角形有两边一角对应
相等时,这两个三角形是否全等的两种情况,得到了全
等 三角形的一种判定方法.
现在,我们讨论两角一边的情况:如果两个三角形
有两个角、一条边分别对应相等,那么这两个三角形全
等吗?与两边一角类似,也会出现两种不同的情况:如图
13.2.8所示,一种情况是两个角及这两角的夹边;另一
种情况是两个角及其中一角的对边.
图 13.2.8 如图13.2.9,已知两个角和一条线段,试画一个三角形,
使这两个角 为其内角,这条线段为这两个角的夹边.
图 13.2.9
把你画的三角形与其他同学画
的三角形 进行比较,或将你画的三做一做步骤:
1.画一条线段AB,
使它等于3 cm;
2.画∠MAB=60°,
∠NBA=40°,MA与NB
交于点C.
△ABC即为所求.
角形剪下,放到其他 同学画的三角形上,看看是
否完全重合.所画 的三角形都全等吗?
换两个角和一条线段,试试看,是否有同样的
结论.
角边角
1.基本事实:两角及其夹边分别相等的两个三角形全
等,简记为A.S.A.(或角边角)
2. 证明书写格式:在△ABC和△A′B′C′中,
∵
∴△ABC≌△A′B′C′.
要点精析:(1)全等的元素:两角及两角夹边;(2)在书
写两个三角形全等的条件角边角时,一定要把夹边相等写
在中间,以突出角边角的位置以及对应关系.
∠A=∠A′,
AB=A′B′,
∠B=∠B′, 例1 如图13.2.11,已知 ∠ABC = ∠DCB,∠ACB=
∠DBC.求证:△ABC≌△DCB,AB=DC.
证明:在△ABC和△DCB中,
∵ABC = ∠DCB (已知),
BC=CB(公共边),
∠ACB =∠DBC(已知), 图13.2.11
∴△ABC≌△DCB (A.S.A.).
AB=DC(全等三角形的对应边相等).(1)在证两三角形全等所需要的角相等时,通常
采用的目前所学过的方法有:(1)公共角、对顶角分
别相等;(2)等角加(减)等角,其和(差)仍相等,即
等式的性质;(3)同角或等角的余(补)角相等;(4)角
平分线得到相等角;(5)平行线的同位角、内错角相
等;(6)直角都相等;(7)全等三角形对应角相等;
(8)第三角代换,即等量代换等.1 如图,∠A=∠B, CA=CB,△CAD和△CBE全等吗? CD和CE相等吗?试说明理由.
2 (中考·安顺)如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )
A.∠A=∠C B.AD=CB
C.BE=DF D.AD∥BC
3 (中考·宁波改编)如图,在四边形ABCD中,AB=CD,AB∥CD,E,F是BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )
A.BE=DF
B.BF=DE
C.AE=CF
D.∠1=∠22知识点判定两三角形全等的定理:角角边
如图13.2. 12,如果两个三角形有
两个角分别对应 相等,且其中一组
相等的角的对边相等,那么这两个
三角 形是否一定全等?
分析:因为三角形的内角和等
于180°,因此有两个 角分别对应思考相等,那么第三个角必定对应相等,于是由 “角边
角”,便可证得这两个三角形全等.
1.定理:两角分别相等且其中一角的对边相等的两个
三角形全等,简记为A.A.S.(或角角边)
证明书写格式:在△ABC和△A′B′C′中,
∵
∴△ABC≌△A′B′C′.
要点精析:(1)全等的元素:两角及其中一角的对边;
(2)用S.A.S. ,A.S.A. ,A.A.S. 证明全等时,要注意图
形中隐含的相等的角.例如:对顶角、公共角、同角的余∠A=∠A′,
∠B=∠B′,
BC=B′C′,角(补角)都是相等的,虽然已知条件无涉及,但证明中
要特别注意挖掘这些重要条件.
(3)常见的全等三角形类型如图13.2--19所示.
图13.2--19
2.已知两角和一边对应相等就可判定两三角形全
等,即“A.S.A.或A.A.S.”
下面我们证明这个定理:
两角分别相等且其中一组等角的对边相等的两个
三角形全等.简记为A. A. S.(或角角边).
已知:如图13. 2. 12, ∠A= ∠A′, ∠B= ∠B′ ,
BC = B′C′ .
求证: △ABC≌△A′B′C′ 证明:∵ ∠A= ∠A′, ∠B= ∠B′ ,(已知),
∠A ′ +∠B ′ + ∠C ′ = 180 ° (三角形的内角和等于
180°),
∴ ∠A +∠B + ∠C ′ = 180 ° (等量代换).
又 ∵ ∠A +∠B + ∠C = 180 °(三角形的内角和等 于
180 °),
∴ ∠C= ∠C′ (等式的性质).
在△ABC 和A′B′C′中,
,
,
,
. 请补充完整证明过程. 例2 如图13.2.13,在△ABC中,D是边BC的中 点, 过点C 画直线CE, 使CE//AB, 交AD的延长线于点 E. 求证AD=ED.
证明:∵ CE//AB(已知),
∴ ∠ ABD = ∠ECD,∠BAD= ∠ CED(两直线
平行,内错角相等).
在△ ABD与△ ECD中,
∵
∴ △ ABD≌△ ECD (A.A.S.),
∴ AD= ED (全等三角形的对应边相等)
∠ ABD = ∠ECD,
∠BAD= ∠ CED(已证),
BD = CD(已知),要证明两条线段AD、ED相等,我们
发现它们分别 属于△ ABD与△ ECD ,
若能证明这两个三角形全等,便可 利
用全等三角形的对应边相等得到要证
明的结论.这就 是通常证明两条线段相
等的一个重要方法.
可以采用类似的方法证明两个角相等. 例3 求证:全等三角形对应边上的高相等.
已知:如图 13.2.14,
△ABC≌△A′B′C′ ,AD、A′D′分别是
△ABC的BC边和△A′B′C′的B′C′边上的
高.求证: AD = A′D′.
你发现AD、
A ′ D ′分别是哪两个三角形的边?这两个三角形全等吗?分析:从图13.2.14中可以看出,AD、 A′D分别属
于△ABD与△A′B′D′ ,要证AD = A′D′,只需
证明这两个三角形全等即可.
证明: ∵ △ABC≌△A′B′C′ (已知),
∴ AB=A′B′(全等三角形的对应边相等),
∵∠ B= ∠B′ (全等三角形的对应角相等).
在△ABD和△A′B′D′中,
∵
∴ △ABD≌△A′B′D′(A.A.S)
∴AD = A′D′ (全等三角形的对应边相等).
∠ ADB= ∠A ′D′ B′ = 90 °(已知),
∠ B= ∠B′ (已证),
AB=A′B′(已证), 判定两三角形全等,先根据已知条件或求证的结论
确定三角形,然后再根据三角形全等的判定方法看缺什
么条件,再去证什么条件,简言之:即综合利用分析法
和综合法寻找证明途径.
全等三角形对应边上的中线、对应角的平分线
又有 什么关系呢?你能说明其中的道理吗?思考 全等三角形除了对应边相等、对应角相等外,
还有以下几条性质:
(1)全等三角形的周长相等,面积相等;
(2)全等三角形的对应边上的中线相等、对应
边上的高线相等、对应角的角平分线相等.1 如图, ∠ 1= ∠2, ∠ C= ∠D. 求证:AC=AD.2 (中考·六盘水)如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
A.∠A=∠D
B.AB=DC
C.∠ACB=∠DBC
D.AC=BD3 (中考·通辽)如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE.求证:△ABC与△DEC全等.
证明三角形全等的“三类条件”:
直接条件:即已知中直接给出的三角形的对应边或
对应角.
隐含条件:即已知没有给出,但通过读图得到的条
件,如公共边、公共角、对顶角.
间接条件:即已知中所给条件不是三角形的对应边
和对应角,需要进一步推理.
