13.2.6 斜边直角边 课件(28张PPT)
文档属性
| 名称 | 13.2.6 斜边直角边 课件(28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 585.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-15 00:00:00 | ||
图片预览







文档简介
课件28张PPT。13.2 三角形全等的判定斜边直角边判定两直角三角形全等的方法—斜边直角边
直角三角形全等的综合判定1知识点判定两直角三角形全等的方法—斜边直角边 我们已经知道,对于两个三角形,如果有“边边角”
分别对应相等,那么不能保证这两个三角形全等.
在两个直角三角形中,当斜边和一条直角边分别对
应相等时,也具有“边边角”对应相等的条件,这时这
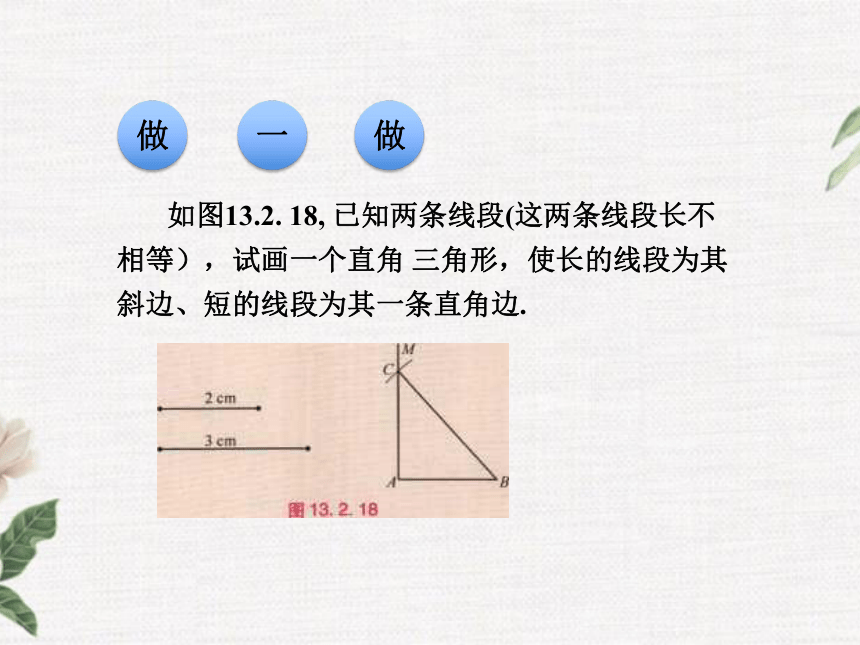
两 个直角三角形是否全等呢?如图13.2. 18, 已知两条线段(这两条线段长不
相等),试画一个直角 三角形,使长的线段为其
斜边、短的线段为其一条直角边.做一做把你画的直角三角形与其他同 学画的直角三角形进行
比较,或将你 画的直角三角形剪下,放到其他同学画的
直角三角形上,看看是否完全重 合.所画的直角三角形都
全等吗? 换两条线段,试试看,是否有同 样的结论?
步骤:
1. 画一条线段AB, 使它等 于 2 cm;
2. 画∠MAB=90°(用量角 器或三角尺);
3. 以点B为圆心、3 cm长 为半径画圆弧,交射线AM
于 点C ;
4.连结BC.
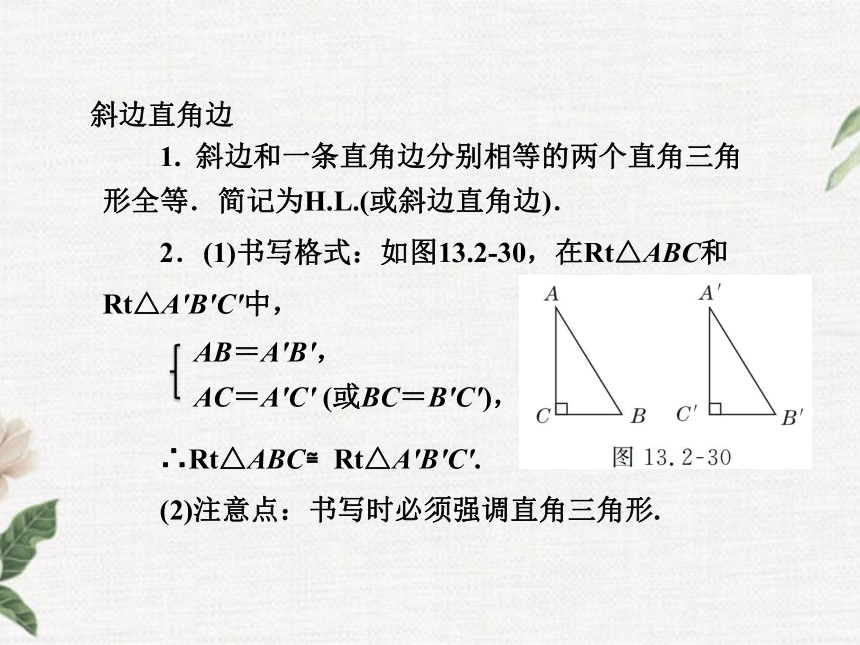
△ABC即为所求. 1. 斜边和一条直角边分别相等的两个直角三角
形全等.简记为H.L.(或斜边直角边).
2.(1)书写格式:如图13.2-30,在Rt△ABC和
Rt△A′B′C′中,
∴Rt△ABC≌Rt△A′B′C′.
(2)注意点:书写时必须强调直角三角形.
AB=A′B′,
AC=A′C′ (或BC=B′C′),斜边直角边 例1 如图 13.2.19,已知AC=FE, ∠C= ∠D= 90°. 求证:BC = AD.
证明:∵ ∠C= ∠D= 90° (已知),
∴△ABC≌△BAD都是直角三
角形(直角三角形的定义) .
在 Rt△ABC 与 Rt△BAD 中,
∵ AB=BA(公共边),
AC=BD(已知),
∴在 Rt△ABC 与 Rt△BAD (H.L.).
∵ BC=AD (全等三角形的对应边相等).
图 13.2.19总 结应用“H.L.”判定两个直角三角形全等,书写时,两个三角形符号前要加上“Rt”.1 如图,在△ABC 中,D为BC的中点, DE丄AB, DF丄AC,点E、F为垂足,DE= DF. 求证: △BDE≌△CFD.2 如图,OD⊥AB于D,OP⊥AC于P,且OD=OP,则△AOD与△AOP全等的理由是( )
A.S.S.S.
B.A.S.A.
C.S.S.A.
D.H.L.3 如图,在△ABC中,∠C=90°,ED⊥AB于点D,BD=BC,若AC=6 cm,则AE+DE等于( )
A.4 cm
B.5 cm
C.6 cm
D.7 cm2知识点直角三角形全等的综合判定 例2 如图13.2--33,已知Rt△ABC≌Rt△ADE,∠ABC =∠ADE=90°,BC与DE相交于点F,连结CD,EB.
求证:CF=EF.图13.2--33导引:(思路1)证CF,EF所在的两个三角形全等.由
Rt△ABC≌Rt△ADE,可得边角相等关系,进
一步证得△ACD≌△AEB,进而证出
△CDF≌△EBF,所以可得CF=EF.
(思路2)要证CF=EF,可证BF=DF.连结AF,
构造两个直角三角形,且AF是公共边,可证得
Rt△ABF≌Rt△ADF,进而得出BF=DF.证明:(方法一)∵Rt△ABC≌Rt△ADE,
∴AC=AE,AB=AD,∠ACB=∠AED,
∠CAB=∠EAD.
∴∠CAB-∠DAB=∠EAD-∠DAB,即
∠DAC=∠BAE.
在△ACD和△AEB中,
AC=AE,
∠DAC=∠BAE,
AD=AB,
∴△ACD≌△AEB(S.A.S.).∴CD=EB,∠ACD=∠AEB.
又∵∠ACB=∠AED,
∴∠ACB-∠ACD=∠AED-∠AEB,
即∠DCF=∠BEF.
在△CDF和△EBF中,
∠DFC=∠BFE,
∠DCF=∠BEF,
CD=EB,
∴△CDF≌△EBF(A.A.S.).
∴CF=EF.(方法二)连结AF.
∵Rt△ABC≌Rt△ADE,∴CB=ED,AB=AD.
在Rt△ADF和Rt△ABF中,
AF=AF,
AD=AB,
∴Rt△ADF≌Rt△ABF(H.L.).
∴DF=BF.
∴CB-BF=ED-DF,即CF=EF. 例3 如图13.2-34所示,在△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且点B,C在AE的两侧,BD⊥AE于点D,CE⊥AE于点E. 图13.2-35图13.2-34(1)求证:BD=DE+CE;
(2)若直线AE绕点A旋转到如图13.2-35①所示的位置(BD
<CE),其余条件不变,则BD与DE,CE的数量关系
如何?请证明.
(3)若直线AE绕A点旋转到如图13.2-35②所示的位置(BD
>CE),其余条件不变,则BD与DE,CE的数量关系
如何?请直接写出结论,不需证明;
(4)根据以上的结论,请用简洁的语言表达BD和DE,CE
的数量关系.导引:在(1)中,直接观察图形可以发现DE+AD=AE,
而要证明的结论是BD=DE+CE,这时如果能证
得AD=CE, BD=AE即可. 而要证AD=CE,
BD=AE,就需证△ABD≌△CAE.
(2)中结论的探索,完全可借助对图形的观察,从
中得到结论再予以证明.
(3)中的结论,可借助观察图形及(2)的结论,直接
给出.
(4)中BD与DE,CE的数量关系,应注意B,C与直
线AE的位置关系,分情况写出结论.?(1)证明:∵BD⊥AE,CE⊥AE,∴∠ADB=∠CEA=90°.
∵∠ABD+∠BAD=∠CAE+∠BAD=90°,
∴∠ABD=∠CAE.
在△ABD和△CAE中,
∠ADB=∠CEA,
∠ABD=∠CAE,
AB=CA,
∴△ABD≌△CAE(A.A.S.),
∴BD=AE,AD=CE,
∵AE=DE+AD,∴BD=DE+CE.(2)解:BD=DE-CE.证明如下:
∵BD⊥AE, CE⊥AE,
∴∠ADB=∠CEA=90°.∵∠BAC=90°,
∴∠ABD+∠BAD=∠CAE+∠BAD=90°,
∴∠ABD=∠CAE.
在△ABD和△CAE中,
∠ADB=∠CEA,
∠ABD=∠CAE,
AB=CA,
∴ △ABD≌△CAE(A.A.S.),∴BD=AE,AD=CE,
∴BD=AE=DE-AD=DE-CE.(3)解:BD=DE-CE.
(4)解:归纳(1)(2)(3)可知,当B,C在AE的两侧时,
BD=DE+CE;
当B,C在AE的同侧时,BD=DE-CE.
?归 纳本题属于图形变化过程中的结论探索性问题,解
这类问题要特别注意图形的变化,从图形的变化中找
出某些不变的特征,猜想其规律,再运用几何知识加
以证明.
归 纳判定直角三角形全等的方法:S.A.S. , A.S.A. ,
A.A.S. , S.S.S. , H.L. , 其中H.L. 仅适用于直角三
角形。1 如图,在△ABC中,AD⊥BC,点D为BC的中点,以下结论:①△ABD≌△ACD;②AB=AC;
③∠B=∠C;④AD是△ABC的角平分线.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
?2 如图,∠ACB=90°,AC=BC,BE⊥CE于点 E,AD⊥CE于点D,下面四个结论:①∠ABE=∠BAD;②△CEB≌△ADC;③AB=CE; ④AD-BE=DE.其中正确的是________.(将你认为正确结论的序号都写上)3 如图,MN∥PQ,AB⊥PQ,点A,D在直线MN上,点B,C在直线PQ上,点E在AB上,AD+BC=7,AD=EB,DE=EC,则AB=________. 判定直角三角形全等的“四种思路”:
(1)若已知条件中有一组直角边和一组斜边分别相等,
用“H.L.”判定.
(2)若有一组锐角和斜边分别相等,用“A.A.S.”判定.
(3)若有一组锐角和一组直角边分别相等,①直角边
是锐角的对边,用“A.A.S.”判定;②直角边是锐角
的邻边,用“A.S.A.”判定.
(4)若有两组直角边分别相等,用“S.A.S.”判定.
直角三角形全等的综合判定1知识点判定两直角三角形全等的方法—斜边直角边 我们已经知道,对于两个三角形,如果有“边边角”
分别对应相等,那么不能保证这两个三角形全等.
在两个直角三角形中,当斜边和一条直角边分别对
应相等时,也具有“边边角”对应相等的条件,这时这
两 个直角三角形是否全等呢?如图13.2. 18, 已知两条线段(这两条线段长不
相等),试画一个直角 三角形,使长的线段为其
斜边、短的线段为其一条直角边.做一做把你画的直角三角形与其他同 学画的直角三角形进行
比较,或将你 画的直角三角形剪下,放到其他同学画的
直角三角形上,看看是否完全重 合.所画的直角三角形都
全等吗? 换两条线段,试试看,是否有同 样的结论?
步骤:
1. 画一条线段AB, 使它等 于 2 cm;
2. 画∠MAB=90°(用量角 器或三角尺);
3. 以点B为圆心、3 cm长 为半径画圆弧,交射线AM
于 点C ;
4.连结BC.
△ABC即为所求. 1. 斜边和一条直角边分别相等的两个直角三角
形全等.简记为H.L.(或斜边直角边).
2.(1)书写格式:如图13.2-30,在Rt△ABC和
Rt△A′B′C′中,
∴Rt△ABC≌Rt△A′B′C′.
(2)注意点:书写时必须强调直角三角形.
AB=A′B′,
AC=A′C′ (或BC=B′C′),斜边直角边 例1 如图 13.2.19,已知AC=FE, ∠C= ∠D= 90°. 求证:BC = AD.
证明:∵ ∠C= ∠D= 90° (已知),
∴△ABC≌△BAD都是直角三
角形(直角三角形的定义) .
在 Rt△ABC 与 Rt△BAD 中,
∵ AB=BA(公共边),
AC=BD(已知),
∴在 Rt△ABC 与 Rt△BAD (H.L.).
∵ BC=AD (全等三角形的对应边相等).
图 13.2.19总 结应用“H.L.”判定两个直角三角形全等,书写时,两个三角形符号前要加上“Rt”.1 如图,在△ABC 中,D为BC的中点, DE丄AB, DF丄AC,点E、F为垂足,DE= DF. 求证: △BDE≌△CFD.2 如图,OD⊥AB于D,OP⊥AC于P,且OD=OP,则△AOD与△AOP全等的理由是( )
A.S.S.S.
B.A.S.A.
C.S.S.A.
D.H.L.3 如图,在△ABC中,∠C=90°,ED⊥AB于点D,BD=BC,若AC=6 cm,则AE+DE等于( )
A.4 cm
B.5 cm
C.6 cm
D.7 cm2知识点直角三角形全等的综合判定 例2 如图13.2--33,已知Rt△ABC≌Rt△ADE,∠ABC =∠ADE=90°,BC与DE相交于点F,连结CD,EB.
求证:CF=EF.图13.2--33导引:(思路1)证CF,EF所在的两个三角形全等.由
Rt△ABC≌Rt△ADE,可得边角相等关系,进
一步证得△ACD≌△AEB,进而证出
△CDF≌△EBF,所以可得CF=EF.
(思路2)要证CF=EF,可证BF=DF.连结AF,
构造两个直角三角形,且AF是公共边,可证得
Rt△ABF≌Rt△ADF,进而得出BF=DF.证明:(方法一)∵Rt△ABC≌Rt△ADE,
∴AC=AE,AB=AD,∠ACB=∠AED,
∠CAB=∠EAD.
∴∠CAB-∠DAB=∠EAD-∠DAB,即
∠DAC=∠BAE.
在△ACD和△AEB中,
AC=AE,
∠DAC=∠BAE,
AD=AB,
∴△ACD≌△AEB(S.A.S.).∴CD=EB,∠ACD=∠AEB.
又∵∠ACB=∠AED,
∴∠ACB-∠ACD=∠AED-∠AEB,
即∠DCF=∠BEF.
在△CDF和△EBF中,
∠DFC=∠BFE,
∠DCF=∠BEF,
CD=EB,
∴△CDF≌△EBF(A.A.S.).
∴CF=EF.(方法二)连结AF.
∵Rt△ABC≌Rt△ADE,∴CB=ED,AB=AD.
在Rt△ADF和Rt△ABF中,
AF=AF,
AD=AB,
∴Rt△ADF≌Rt△ABF(H.L.).
∴DF=BF.
∴CB-BF=ED-DF,即CF=EF. 例3 如图13.2-34所示,在△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且点B,C在AE的两侧,BD⊥AE于点D,CE⊥AE于点E. 图13.2-35图13.2-34(1)求证:BD=DE+CE;
(2)若直线AE绕点A旋转到如图13.2-35①所示的位置(BD
<CE),其余条件不变,则BD与DE,CE的数量关系
如何?请证明.
(3)若直线AE绕A点旋转到如图13.2-35②所示的位置(BD
>CE),其余条件不变,则BD与DE,CE的数量关系
如何?请直接写出结论,不需证明;
(4)根据以上的结论,请用简洁的语言表达BD和DE,CE
的数量关系.导引:在(1)中,直接观察图形可以发现DE+AD=AE,
而要证明的结论是BD=DE+CE,这时如果能证
得AD=CE, BD=AE即可. 而要证AD=CE,
BD=AE,就需证△ABD≌△CAE.
(2)中结论的探索,完全可借助对图形的观察,从
中得到结论再予以证明.
(3)中的结论,可借助观察图形及(2)的结论,直接
给出.
(4)中BD与DE,CE的数量关系,应注意B,C与直
线AE的位置关系,分情况写出结论.?(1)证明:∵BD⊥AE,CE⊥AE,∴∠ADB=∠CEA=90°.
∵∠ABD+∠BAD=∠CAE+∠BAD=90°,
∴∠ABD=∠CAE.
在△ABD和△CAE中,
∠ADB=∠CEA,
∠ABD=∠CAE,
AB=CA,
∴△ABD≌△CAE(A.A.S.),
∴BD=AE,AD=CE,
∵AE=DE+AD,∴BD=DE+CE.(2)解:BD=DE-CE.证明如下:
∵BD⊥AE, CE⊥AE,
∴∠ADB=∠CEA=90°.∵∠BAC=90°,
∴∠ABD+∠BAD=∠CAE+∠BAD=90°,
∴∠ABD=∠CAE.
在△ABD和△CAE中,
∠ADB=∠CEA,
∠ABD=∠CAE,
AB=CA,
∴ △ABD≌△CAE(A.A.S.),∴BD=AE,AD=CE,
∴BD=AE=DE-AD=DE-CE.(3)解:BD=DE-CE.
(4)解:归纳(1)(2)(3)可知,当B,C在AE的两侧时,
BD=DE+CE;
当B,C在AE的同侧时,BD=DE-CE.
?归 纳本题属于图形变化过程中的结论探索性问题,解
这类问题要特别注意图形的变化,从图形的变化中找
出某些不变的特征,猜想其规律,再运用几何知识加
以证明.
归 纳判定直角三角形全等的方法:S.A.S. , A.S.A. ,
A.A.S. , S.S.S. , H.L. , 其中H.L. 仅适用于直角三
角形。1 如图,在△ABC中,AD⊥BC,点D为BC的中点,以下结论:①△ABD≌△ACD;②AB=AC;
③∠B=∠C;④AD是△ABC的角平分线.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
?2 如图,∠ACB=90°,AC=BC,BE⊥CE于点 E,AD⊥CE于点D,下面四个结论:①∠ABE=∠BAD;②△CEB≌△ADC;③AB=CE; ④AD-BE=DE.其中正确的是________.(将你认为正确结论的序号都写上)3 如图,MN∥PQ,AB⊥PQ,点A,D在直线MN上,点B,C在直线PQ上,点E在AB上,AD+BC=7,AD=EB,DE=EC,则AB=________. 判定直角三角形全等的“四种思路”:
(1)若已知条件中有一组直角边和一组斜边分别相等,
用“H.L.”判定.
(2)若有一组锐角和斜边分别相等,用“A.A.S.”判定.
(3)若有一组锐角和一组直角边分别相等,①直角边
是锐角的对边,用“A.A.S.”判定;②直角边是锐角
的邻边,用“A.S.A.”判定.
(4)若有两组直角边分别相等,用“S.A.S.”判定.
