13.3.1 等腰三角形的性质 课件(31张PPT)
文档属性
| 名称 | 13.3.1 等腰三角形的性质 课件(31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 658.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-15 14:52:58 | ||
图片预览











文档简介
课件31张PPT。13.3 等腰三角形等腰三角形的性质第13章 全等三角形等腰三角形边角性质:等边对等角
等腰三角形的轴对称性:三线合一1知识点等腰三角形边角性质:等边对等角
等腰三角形的定义及有关概念:
1. 定义:有两条边相等的三角形叫做等腰三角形.
2. 有关概念:等腰三角形中,相等的两边都叫做腰,
另一边叫做底边,两腰的夹角叫做顶角,腰和底边
的夹角叫做底角.
例1 〈分类讨论题〉等腰三角形的周长为50 cm,一条边长是12 cm,求另两条边长.
导引:已知一条边长为12 cm,由于不确定已知的边
是腰还是底边,所以要分两种情况讨论.
解: 当腰长为12 cm时,设底边长为x cm,
∵x+2×12=50,∴x=26.
当底边长为12 cm时,设腰长为y cm,
∵2y+12=50,∴y=19.当腰长为12 cm时,
∵12+12=24<26,∴不满足三角形任意两边之和大
于第三边.
当底边长为12 cm时,三角形三条边长分别为12 cm,
19 cm,19 cm,
满足三角形任意两边之和大于第三边,
∴这个等腰三角形另两条边长分别为19 cm,19 cm.归 纳 在等腰三角形中求某一条边长时,若已知的边
和所要求的边是腰还是底边不确定,则要运用分类
讨论思想,分情况讨论求解. 剪一张等腰三角形的半透明纸片,每人所剪的等腰三角
形的大小和形状可以不一样,如图13.3.2,把纸片对折,让
两腰AB、AC 重叠在一起, 折痕为AD 你能发现什么现象吗?做一做性质1:等腰三角形的两底角相等(简写成“等边
对等角”).
要点精析:(1)适用条件:必须在同一个三角形
中.(2)应用格式:在△ABC中,因为AB=AC,所
以∠B=∠C. (3)作用:它是证明角相等常用的方
法, 它的应用可省去三角形全等的证明, 因而 更
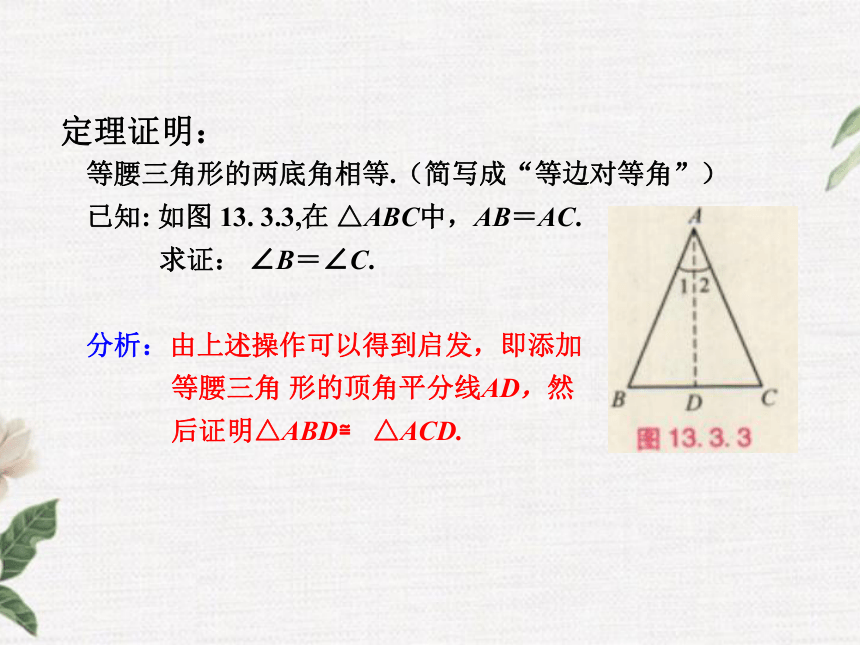
简便.等腰三角形的性质等腰三角形的两底角相等.(简写成“等边对等角”)
已知: 如图 13. 3.3,在 △ABC中,AB=AC.
求证: ∠B=∠C.
分析:由上述操作可以得到启发,即添加
等腰三角 形的顶角平分线AD,然
后证明△ABD≌ △ACD.定理证明:证明:画∠ABC的平分线AD.
在 △ABD和 △ACD中,
∵ AB=AC (已知),
∠ 1 = ∠ 2(角平分线的定义),
AD =AD (公共边),
∴ △ABD≌ △ACD(S.A.S.).
∴ ∠B=∠C(全等三角形的对应角相等)? 例2 已知:在△ABC中, AB=AC , ∠B =80°.求 ∠C和∠A的大小.
解: ∵ AB=AC (已知),
∴ ∠C=∠B = 80°(等边对等角).
又∵ ∠A + ∠B + ∠C = 180°(三角形的内角和
等于 180 ° ),
∴ ∠A = 180 ° - ∠B - ∠C (等式的性质)
= 180° - 80° - 80° = 20°. 例3 (1) 在△ABC中,AB=AC,若∠A=50°,求∠B;
(2)若等腰三角形的一个角为70°,求顶角的度数;
(3)若等腰三角形的一个角为90°,求顶角的度数.导引:给出的条件中,若底角、顶角已确定,可直接
运用三角形的内角和定理与等腰三角形的两底
角相等的性质求解;若给出的条件中底角、顶
角不确定,则要分两种情况求解.解:(1)∵AB=AC,
∴∠B=∠C.
∵∠A+∠B+∠C=180°,
∴50°+2∠B=180°,解得∠B=65°.
(2)当底角为70°时,顶角为180°-70°×2=40°.
当顶角为70°时,底角为 =55°.
因此顶角为40°或70°.(3)若顶角为90°,底角为 =45°.
若底角为90°,则三个内角的和将大于180°,
不符合三角形内角和定理.因此顶角为90°.总 结 (1)在等腰三角形中求角时,要看给出的角是否
确定为顶角或底角.若已确定,则直接利用三角形
的内角和定理求解;若没有指出所给的角是顶角还
是底角,要分两种情况讨论,并看是否符合三角形
内角和定理.(2)若等腰三角形中给出的一内角是直
角或钝角,则此角必为顶角.1 填空:
(1)如果等腰三角形的一个底角为50°,那么其余两个角的大小分别为 和 ;
(2)如果等腰三角形的顶角为80°,那么它的一个底角的大小为和 . 2 (中考·广西)如图,在△ABC中,AB=AC,∠BAC=100°,AB 的垂直平分线DE分别交AB、BC于点D 、 E,则∠BAE=( )
A.80° B.60° C.50° D.40 3 (中考·丹东)如图,在△ABC中,AB=AC,∠A=30°,E为BC的延长线上一点,∠ABC与∠ACE的平分线交于点D,则∠D的度数为( )
A.15° B.17.5° C.20° D.22.5°
?2知识点等腰三角形的轴对称性:三线合一由前面的“做一做”,你还可以发现什么结论?请
写 出你的发现:
;
;
.探索性质2:等腰三角形底边上的高、中线及顶角的平
分线互相重合 (简称“三线合一”).
要点解析:(1)含义:这是等腰三角形所特有的性
质,它实际是一组定理,应用过程中,在三角形是等腰
三角形前提下,“顶角的平分线、底边上的中线、底边上的高” 只要知道其中 “一线 ”,就可以说明是其他 “两线”.
(2)作用:是证明线段相等、角相等、垂直等关系
的重要方法,应用广泛.(3)对称性:等腰三角形是轴对称图形,顶角平分
线(或底边上的高、底边上的中线)所在的直线是它的对
称轴.
(4)应用格式:如图13.3--1,在△ABC中,
①∵AB=AC,AD⊥BC,
∴AD平分∠BAC(或BD=CD);
②∵AB=AC,BD=DC,
∴AD⊥BC(或AD平分∠BAC);
③∵AB=AC,AD平分∠BAC, 图13.3--1
∴BD=DC(或AD⊥BC).总 结1. 等腰三角形“三线合一”的性质包含三层含义:
(1)已知等腰三角形底边上的中线,则它平分顶角,垂
直于底边;
(2)已知等腰三角形顶角的平分线,则它垂直平分底边;
(3)已知等腰三角形底边上的高,则它平分底边,平分
顶角.
2.等腰三角形“三线合一”的性质常常可以用来证明角相
等、线段相等和线段垂直.在遇到等腰三角形的问题时,
尝试作这条辅助线,常常会有意想不到的效果. 例4 如图 13.3.4,在△ABC中, AB=AC ,D是BC 边上的中点, ∠B =30°.求 :
(1)∠ADC的大小;
(2)∠1的大小.
解: (1)∵ AB=AC ,BD=DC (已知),
∴AD ⊥BC (等腰三角形的“三线合一”)
∠ADC=∠ADB = 90°.(2)∵ ∠1+ ∠B + ∠ ADB= 180°(三角形的内角和
等于 180 ° ),
∠B = 30 ° (已知),
∴ ∠1 = 180 ° -∠B -∠ ADB (等式的性质)
= 180° - 30° - 90° = 60°.
例5 如图13.3--2,在△ABC中,
AB=AC,AD是BC边上
的中线.若∠BAD=25°,
求∠C的度数.
解:∵AB=AC,AD是BC边上的中线,
∴∠BAD=∠CAD,
∴∠BAC=2∠BAD=50°.
∵AB=AC,
∴ ∠C=∠ABC = ×(180°-∠A)=
×(180°-50°)=65°. 图13.3--2总 结等腰三角形的“三线合一”的性质是证明角相等、线
段相等和垂直关系的重要依据;因为题目的证明或
计算所求结果大多都是单一的,所以“三线合一”的
性质的应用也是单一的,一般得出一个结论,因此
应用要灵活.
(2) 在等腰三角形中,作“三线”中“一线”,利用“三线合
一”是解决有关等腰三角形问题常用的方法.1 如图,在△ABC中,AB=AC,点D是BC边的中点,点E在AD上,那么下列结论不一定正确的是( )
A.AD⊥BC
B.∠EBC=∠ECB
C.∠ABE=∠ACE
D.AE=BE2 如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,DF⊥AC于点F,下列结论:①∠BAD=∠CAD;②BD=CD;③若点P在直线AD上,则PB=PC.其中正确的是( )
A.①
B.②
C.①②
D.①②③3 如图,在△ABC中,AB=AC,点D,E在BC上,连接AD,AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( )
A.BD=CE B.AD=AE
C.DA=DE D.BE=CD1.等腰三角形的性质1:等边对等角.
2.等腰三角形的性质2:三线合一.
等腰三角形的轴对称性:三线合一1知识点等腰三角形边角性质:等边对等角
等腰三角形的定义及有关概念:
1. 定义:有两条边相等的三角形叫做等腰三角形.
2. 有关概念:等腰三角形中,相等的两边都叫做腰,
另一边叫做底边,两腰的夹角叫做顶角,腰和底边
的夹角叫做底角.
例1 〈分类讨论题〉等腰三角形的周长为50 cm,一条边长是12 cm,求另两条边长.
导引:已知一条边长为12 cm,由于不确定已知的边
是腰还是底边,所以要分两种情况讨论.
解: 当腰长为12 cm时,设底边长为x cm,
∵x+2×12=50,∴x=26.
当底边长为12 cm时,设腰长为y cm,
∵2y+12=50,∴y=19.当腰长为12 cm时,
∵12+12=24<26,∴不满足三角形任意两边之和大
于第三边.
当底边长为12 cm时,三角形三条边长分别为12 cm,
19 cm,19 cm,
满足三角形任意两边之和大于第三边,
∴这个等腰三角形另两条边长分别为19 cm,19 cm.归 纳 在等腰三角形中求某一条边长时,若已知的边
和所要求的边是腰还是底边不确定,则要运用分类
讨论思想,分情况讨论求解. 剪一张等腰三角形的半透明纸片,每人所剪的等腰三角
形的大小和形状可以不一样,如图13.3.2,把纸片对折,让
两腰AB、AC 重叠在一起, 折痕为AD 你能发现什么现象吗?做一做性质1:等腰三角形的两底角相等(简写成“等边
对等角”).
要点精析:(1)适用条件:必须在同一个三角形
中.(2)应用格式:在△ABC中,因为AB=AC,所
以∠B=∠C. (3)作用:它是证明角相等常用的方
法, 它的应用可省去三角形全等的证明, 因而 更
简便.等腰三角形的性质等腰三角形的两底角相等.(简写成“等边对等角”)
已知: 如图 13. 3.3,在 △ABC中,AB=AC.
求证: ∠B=∠C.
分析:由上述操作可以得到启发,即添加
等腰三角 形的顶角平分线AD,然
后证明△ABD≌ △ACD.定理证明:证明:画∠ABC的平分线AD.
在 △ABD和 △ACD中,
∵ AB=AC (已知),
∠ 1 = ∠ 2(角平分线的定义),
AD =AD (公共边),
∴ △ABD≌ △ACD(S.A.S.).
∴ ∠B=∠C(全等三角形的对应角相等)? 例2 已知:在△ABC中, AB=AC , ∠B =80°.求 ∠C和∠A的大小.
解: ∵ AB=AC (已知),
∴ ∠C=∠B = 80°(等边对等角).
又∵ ∠A + ∠B + ∠C = 180°(三角形的内角和
等于 180 ° ),
∴ ∠A = 180 ° - ∠B - ∠C (等式的性质)
= 180° - 80° - 80° = 20°. 例3 (1) 在△ABC中,AB=AC,若∠A=50°,求∠B;
(2)若等腰三角形的一个角为70°,求顶角的度数;
(3)若等腰三角形的一个角为90°,求顶角的度数.导引:给出的条件中,若底角、顶角已确定,可直接
运用三角形的内角和定理与等腰三角形的两底
角相等的性质求解;若给出的条件中底角、顶
角不确定,则要分两种情况求解.解:(1)∵AB=AC,
∴∠B=∠C.
∵∠A+∠B+∠C=180°,
∴50°+2∠B=180°,解得∠B=65°.
(2)当底角为70°时,顶角为180°-70°×2=40°.
当顶角为70°时,底角为 =55°.
因此顶角为40°或70°.(3)若顶角为90°,底角为 =45°.
若底角为90°,则三个内角的和将大于180°,
不符合三角形内角和定理.因此顶角为90°.总 结 (1)在等腰三角形中求角时,要看给出的角是否
确定为顶角或底角.若已确定,则直接利用三角形
的内角和定理求解;若没有指出所给的角是顶角还
是底角,要分两种情况讨论,并看是否符合三角形
内角和定理.(2)若等腰三角形中给出的一内角是直
角或钝角,则此角必为顶角.1 填空:
(1)如果等腰三角形的一个底角为50°,那么其余两个角的大小分别为 和 ;
(2)如果等腰三角形的顶角为80°,那么它的一个底角的大小为和 . 2 (中考·广西)如图,在△ABC中,AB=AC,∠BAC=100°,AB 的垂直平分线DE分别交AB、BC于点D 、 E,则∠BAE=( )
A.80° B.60° C.50° D.40 3 (中考·丹东)如图,在△ABC中,AB=AC,∠A=30°,E为BC的延长线上一点,∠ABC与∠ACE的平分线交于点D,则∠D的度数为( )
A.15° B.17.5° C.20° D.22.5°
?2知识点等腰三角形的轴对称性:三线合一由前面的“做一做”,你还可以发现什么结论?请
写 出你的发现:
;
;
.探索性质2:等腰三角形底边上的高、中线及顶角的平
分线互相重合 (简称“三线合一”).
要点解析:(1)含义:这是等腰三角形所特有的性
质,它实际是一组定理,应用过程中,在三角形是等腰
三角形前提下,“顶角的平分线、底边上的中线、底边上的高” 只要知道其中 “一线 ”,就可以说明是其他 “两线”.
(2)作用:是证明线段相等、角相等、垂直等关系
的重要方法,应用广泛.(3)对称性:等腰三角形是轴对称图形,顶角平分
线(或底边上的高、底边上的中线)所在的直线是它的对
称轴.
(4)应用格式:如图13.3--1,在△ABC中,
①∵AB=AC,AD⊥BC,
∴AD平分∠BAC(或BD=CD);
②∵AB=AC,BD=DC,
∴AD⊥BC(或AD平分∠BAC);
③∵AB=AC,AD平分∠BAC, 图13.3--1
∴BD=DC(或AD⊥BC).总 结1. 等腰三角形“三线合一”的性质包含三层含义:
(1)已知等腰三角形底边上的中线,则它平分顶角,垂
直于底边;
(2)已知等腰三角形顶角的平分线,则它垂直平分底边;
(3)已知等腰三角形底边上的高,则它平分底边,平分
顶角.
2.等腰三角形“三线合一”的性质常常可以用来证明角相
等、线段相等和线段垂直.在遇到等腰三角形的问题时,
尝试作这条辅助线,常常会有意想不到的效果. 例4 如图 13.3.4,在△ABC中, AB=AC ,D是BC 边上的中点, ∠B =30°.求 :
(1)∠ADC的大小;
(2)∠1的大小.
解: (1)∵ AB=AC ,BD=DC (已知),
∴AD ⊥BC (等腰三角形的“三线合一”)
∠ADC=∠ADB = 90°.(2)∵ ∠1+ ∠B + ∠ ADB= 180°(三角形的内角和
等于 180 ° ),
∠B = 30 ° (已知),
∴ ∠1 = 180 ° -∠B -∠ ADB (等式的性质)
= 180° - 30° - 90° = 60°.
例5 如图13.3--2,在△ABC中,
AB=AC,AD是BC边上
的中线.若∠BAD=25°,
求∠C的度数.
解:∵AB=AC,AD是BC边上的中线,
∴∠BAD=∠CAD,
∴∠BAC=2∠BAD=50°.
∵AB=AC,
∴ ∠C=∠ABC = ×(180°-∠A)=
×(180°-50°)=65°. 图13.3--2总 结等腰三角形的“三线合一”的性质是证明角相等、线
段相等和垂直关系的重要依据;因为题目的证明或
计算所求结果大多都是单一的,所以“三线合一”的
性质的应用也是单一的,一般得出一个结论,因此
应用要灵活.
(2) 在等腰三角形中,作“三线”中“一线”,利用“三线合
一”是解决有关等腰三角形问题常用的方法.1 如图,在△ABC中,AB=AC,点D是BC边的中点,点E在AD上,那么下列结论不一定正确的是( )
A.AD⊥BC
B.∠EBC=∠ECB
C.∠ABE=∠ACE
D.AE=BE2 如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,DF⊥AC于点F,下列结论:①∠BAD=∠CAD;②BD=CD;③若点P在直线AD上,则PB=PC.其中正确的是( )
A.①
B.②
C.①②
D.①②③3 如图,在△ABC中,AB=AC,点D,E在BC上,连接AD,AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( )
A.BD=CE B.AD=AE
C.DA=DE D.BE=CD1.等腰三角形的性质1:等边对等角.
2.等腰三角形的性质2:三线合一.
