13.3.2 等腰三角形的判定 课件(23张PPT)
文档属性
| 名称 | 13.3.2 等腰三角形的判定 课件(23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 539.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-15 14:52:58 | ||
图片预览








文档简介
课件23张PPT。第13章 全等三角形13.3 等腰三角形等腰三角形的判定等腰三角形的判定
等腰三角形的判定与性质 对于一个三角形,怎样判定它是不是等腰三
角形呢? 我们已经知道的方法是按定义,看它是
否有两条边相等. 现在再看看能否找到其他的判
定方法.1知识点等腰三角形的判定
我们知道,等腰三角形的两个底角相等.反过来,在一 个三角形
中,如果有两个角相等,那么它是等腰三角形吗?
画画看,你发现了什么?
我们可以发现,如果一个三角形中有两个角相等,那 么它就是
等腰三角形.即
如果一个三角形有两个角相等,那么这两个角所对 的边也相等.
(简写成“等角对等边”)(来源于教材)探索判定定理:如果一个三角形有两个角相等,那么
这两个角所对的边也相等.(简写成“等角对等边”)
应用格式:在△ABC中,∵∠B=∠C, ∴AB=AC.
定理 证明:
已知:如图13. 3. 6, △ABC中, ∠B=∠C.
求证: AB=AC.
分析:要证明AB=AC ,可设法构造两
个全等三角 ,使 AB、AC分别
是这两个全等三角形的对应边,
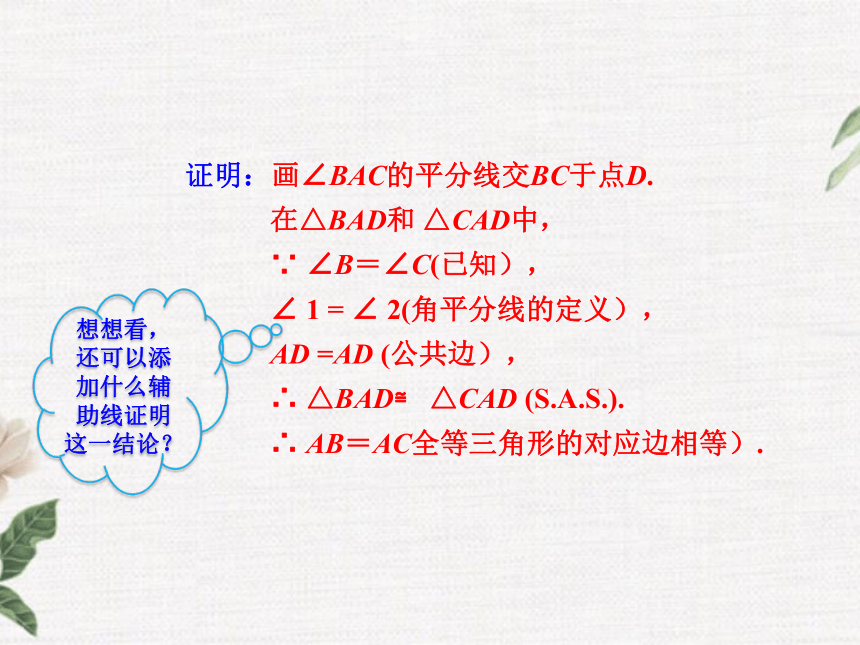
于是 想到画∠BAC的平分线AD.证明:画∠BAC的平分线交BC于点D.
在△BAD和 △CAD中,
∵ ∠B=∠C(已知),
∠ 1 = ∠ 2(角平分线的定义),
AD =AD (公共边),
∴ △BAD≌ △CAD (S.A.S.).
∴ AB=AC全等三角形的对应边相等).
想想看,还可以添加什么辅助线证明这一结论? 例1 如图13.3.7, 在△ABC中, 已知∠A= 40° ,∠B = 70°. 求证: AB=AC .
证明:∵ ∠A + ∠B + ∠C = 180°(三角形的
内角和等于 180 ° ),
∠A= 40° ,∠B = 70°(已知),
∴ ∠C = 180 ° - ∠A - ∠B (等式的
性质)
= 180° - 40° - 70° = 70°.
∴ ∠C = 180 ° - ∠A - ∠B (等量代换),
AB=AC(等边对等角). 例2 如图13.3--10,在△ABC中,∠ABC,∠CAB的平分线交于点P,过点P作DE∥AB,分别交BC,AC于点D,E.
求证:DE=BD+AE.图13.3--10导引:要证: DE=BD+AE ,而由图13.3--10知
DE=DP+PE.因此只需证:
BD+AE=DP+PE即可.
即需证BD=DP,AE=PE,
而要证这两边相等,只需证明它们所对的角
相等;因此我们可以从证角相等作为切入口
进行证明.证明:∵DE∥AB,
∴∠ABP=∠DPB, ∠BAP=∠EPA.
∵∠ABC,∠CAB的平分线交于点P,
∴∠ABP=∠DBP, ∠BAP=∠EAP,
∴∠DBP=∠DPB, ∠EAP=∠EPA,
∴DP=DB,EP=EA,
∴DP+EP=DB+EA,即DE=BD+AE.
归 纳 (1)本题运用平行线性质以及角平分线的定义,
证明角之间的相等关系,进而运用等腰三角形的判
定得出线段之间的长度关系,这是证几何题中常用
的方法.(2)如图13.3--10中角的一边与角的平分线及
角另一边的平行线所构成的三角形是等腰三角形,
这是一个基本的图形,在以后学习平行四边形中会
经常遇到.1 在△ABC中,∠A和∠B的度数如下,能判定△ABC是等腰三角形的是( )
A.∠A=50°,∠B=70°
B.∠A=70°,∠B=40°
C.∠A=30°,∠B=90°
D.∠A=80°,∠B=60°2 如图,∠B=∠C=36°,∠ADE=∠AED=72°,则图中的等腰三角形有( )
A.3个
B.4个
C.5个
D.6个3 (中考·陕西)如图,在△ABC中,∠A=36°,AB=AC,BD是△ABC的角平分线,若在边AB上截取BE=BC,连接DE,则图中等腰三角形共有( )
A.2个
B.3个
C.4个
D.5个
2知识点等腰三角形的判定与性质等腰三角形的判定与性质的异同
相同点:都是在一个三角形中;
区别:判定是由角到边,性质是由边到角.即:
等边 等角.性质
判定 例3 如图13.3--11,在△ABC中,AB=AC,EF交 AB于点E,交AC的延长线于点F,交BC于点D,且BE=CF. 求证:DE=DF.
导引:要证DE=DF,可构造以DE
和DF为对应边的全等三角形,
不妨过点E作EG∥AC交BC于
点G,则只要证明△EDG≌
△FDC即可,缺少的条件可
用等腰三角形的性质及判定得出.
?图13.3--11证明:过点E作EG∥AC交BC于点G,
如图13.3--12,则∠1=∠F,∠2=∠3.
∵AB=AC,∴∠B=∠3(等边对等角).
∴∠B=∠2.∴BE=EG(等角对等边).
又∵BE=CF,∴EG=CF.
在△EDG和△FDC中,
∠4=∠5,
∠1=∠F,
EG=FC,
∴△EDG≌△FDC.∴DE=DF.图13.3--12总 结证明线段(或角)相等,以其中一边(或角)所在三角
形作为“基础三角形”在另一边(或角)上作与其全等的三
角形是常用的作辅助线的方法;如本例是以DF所在的
△DFC为“基础三角形”,以DE为边作与△DFC全等的
△DEG;若以DE所在的△DEB为“基础三角形”,以DF
为边作与△DEB全等的△DFG怎么作请读者试一试.1 (中考·泰安)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )
A.4个
B.3个
C.2个
D.1个2 如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=6,则线段MN的长为( )
A.6
B.7
C.8
D.93 在下列三角形中,若AB=AC,则不能被一条直线分成两个小等腰三角形的是( ) 等腰三角形的两种判定方法:
(1)当三角形有两条边相等时,应用“有两条边相
等的三角形是等腰三角形”来判定.
(2)当三角形中有两个角相等时,应用“如果一个
三角形有两个角相等,那么这两个角所对的边也相等”
来证明.
等腰三角形的判定与性质 对于一个三角形,怎样判定它是不是等腰三
角形呢? 我们已经知道的方法是按定义,看它是
否有两条边相等. 现在再看看能否找到其他的判
定方法.1知识点等腰三角形的判定
我们知道,等腰三角形的两个底角相等.反过来,在一 个三角形
中,如果有两个角相等,那么它是等腰三角形吗?
画画看,你发现了什么?
我们可以发现,如果一个三角形中有两个角相等,那 么它就是
等腰三角形.即
如果一个三角形有两个角相等,那么这两个角所对 的边也相等.
(简写成“等角对等边”)(来源于教材)探索判定定理:如果一个三角形有两个角相等,那么
这两个角所对的边也相等.(简写成“等角对等边”)
应用格式:在△ABC中,∵∠B=∠C, ∴AB=AC.
定理 证明:
已知:如图13. 3. 6, △ABC中, ∠B=∠C.
求证: AB=AC.
分析:要证明AB=AC ,可设法构造两
个全等三角 ,使 AB、AC分别
是这两个全等三角形的对应边,
于是 想到画∠BAC的平分线AD.证明:画∠BAC的平分线交BC于点D.
在△BAD和 △CAD中,
∵ ∠B=∠C(已知),
∠ 1 = ∠ 2(角平分线的定义),
AD =AD (公共边),
∴ △BAD≌ △CAD (S.A.S.).
∴ AB=AC全等三角形的对应边相等).
想想看,还可以添加什么辅助线证明这一结论? 例1 如图13.3.7, 在△ABC中, 已知∠A= 40° ,∠B = 70°. 求证: AB=AC .
证明:∵ ∠A + ∠B + ∠C = 180°(三角形的
内角和等于 180 ° ),
∠A= 40° ,∠B = 70°(已知),
∴ ∠C = 180 ° - ∠A - ∠B (等式的
性质)
= 180° - 40° - 70° = 70°.
∴ ∠C = 180 ° - ∠A - ∠B (等量代换),
AB=AC(等边对等角). 例2 如图13.3--10,在△ABC中,∠ABC,∠CAB的平分线交于点P,过点P作DE∥AB,分别交BC,AC于点D,E.
求证:DE=BD+AE.图13.3--10导引:要证: DE=BD+AE ,而由图13.3--10知
DE=DP+PE.因此只需证:
BD+AE=DP+PE即可.
即需证BD=DP,AE=PE,
而要证这两边相等,只需证明它们所对的角
相等;因此我们可以从证角相等作为切入口
进行证明.证明:∵DE∥AB,
∴∠ABP=∠DPB, ∠BAP=∠EPA.
∵∠ABC,∠CAB的平分线交于点P,
∴∠ABP=∠DBP, ∠BAP=∠EAP,
∴∠DBP=∠DPB, ∠EAP=∠EPA,
∴DP=DB,EP=EA,
∴DP+EP=DB+EA,即DE=BD+AE.
归 纳 (1)本题运用平行线性质以及角平分线的定义,
证明角之间的相等关系,进而运用等腰三角形的判
定得出线段之间的长度关系,这是证几何题中常用
的方法.(2)如图13.3--10中角的一边与角的平分线及
角另一边的平行线所构成的三角形是等腰三角形,
这是一个基本的图形,在以后学习平行四边形中会
经常遇到.1 在△ABC中,∠A和∠B的度数如下,能判定△ABC是等腰三角形的是( )
A.∠A=50°,∠B=70°
B.∠A=70°,∠B=40°
C.∠A=30°,∠B=90°
D.∠A=80°,∠B=60°2 如图,∠B=∠C=36°,∠ADE=∠AED=72°,则图中的等腰三角形有( )
A.3个
B.4个
C.5个
D.6个3 (中考·陕西)如图,在△ABC中,∠A=36°,AB=AC,BD是△ABC的角平分线,若在边AB上截取BE=BC,连接DE,则图中等腰三角形共有( )
A.2个
B.3个
C.4个
D.5个
2知识点等腰三角形的判定与性质等腰三角形的判定与性质的异同
相同点:都是在一个三角形中;
区别:判定是由角到边,性质是由边到角.即:
等边 等角.性质
判定 例3 如图13.3--11,在△ABC中,AB=AC,EF交 AB于点E,交AC的延长线于点F,交BC于点D,且BE=CF. 求证:DE=DF.
导引:要证DE=DF,可构造以DE
和DF为对应边的全等三角形,
不妨过点E作EG∥AC交BC于
点G,则只要证明△EDG≌
△FDC即可,缺少的条件可
用等腰三角形的性质及判定得出.
?图13.3--11证明:过点E作EG∥AC交BC于点G,
如图13.3--12,则∠1=∠F,∠2=∠3.
∵AB=AC,∴∠B=∠3(等边对等角).
∴∠B=∠2.∴BE=EG(等角对等边).
又∵BE=CF,∴EG=CF.
在△EDG和△FDC中,
∠4=∠5,
∠1=∠F,
EG=FC,
∴△EDG≌△FDC.∴DE=DF.图13.3--12总 结证明线段(或角)相等,以其中一边(或角)所在三角
形作为“基础三角形”在另一边(或角)上作与其全等的三
角形是常用的作辅助线的方法;如本例是以DF所在的
△DFC为“基础三角形”,以DE为边作与△DFC全等的
△DEG;若以DE所在的△DEB为“基础三角形”,以DF
为边作与△DEB全等的△DFG怎么作请读者试一试.1 (中考·泰安)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )
A.4个
B.3个
C.2个
D.1个2 如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=6,则线段MN的长为( )
A.6
B.7
C.8
D.93 在下列三角形中,若AB=AC,则不能被一条直线分成两个小等腰三角形的是( ) 等腰三角形的两种判定方法:
(1)当三角形有两条边相等时,应用“有两条边相
等的三角形是等腰三角形”来判定.
(2)当三角形中有两个角相等时,应用“如果一个
三角形有两个角相等,那么这两个角所对的边也相等”
来证明.
