人教版高中数学文科选修1-1同步练习题、期中、期末复习资料、补习资料:05【基础】简单的逻辑联结词
文档属性
| 名称 | 人教版高中数学文科选修1-1同步练习题、期中、期末复习资料、补习资料:05【基础】简单的逻辑联结词 |
|
|
| 格式 | zip | ||
| 文件大小 | 182.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-18 11:46:19 | ||
图片预览





文档简介
1简单的逻辑联结词
【学习目标】
1.了解逻辑联结词“或”、“且”、“非”的含义;
2. 会用逻辑联结词“或”、“且”、“非”联结两个命题或改写某些数学命题,并判断命题的真假.
【要点梳理】
要点一、逻辑联结词“且”
一般地,用逻辑联结词“且”把命题和联结起来得到一个新命题,记作:,读作:“且”。
规定:当,两命题有一个命题是假命题时,是假命题;
当,两命题都是真命题时,是真命题。
要点诠释:
的真假判定的理解:
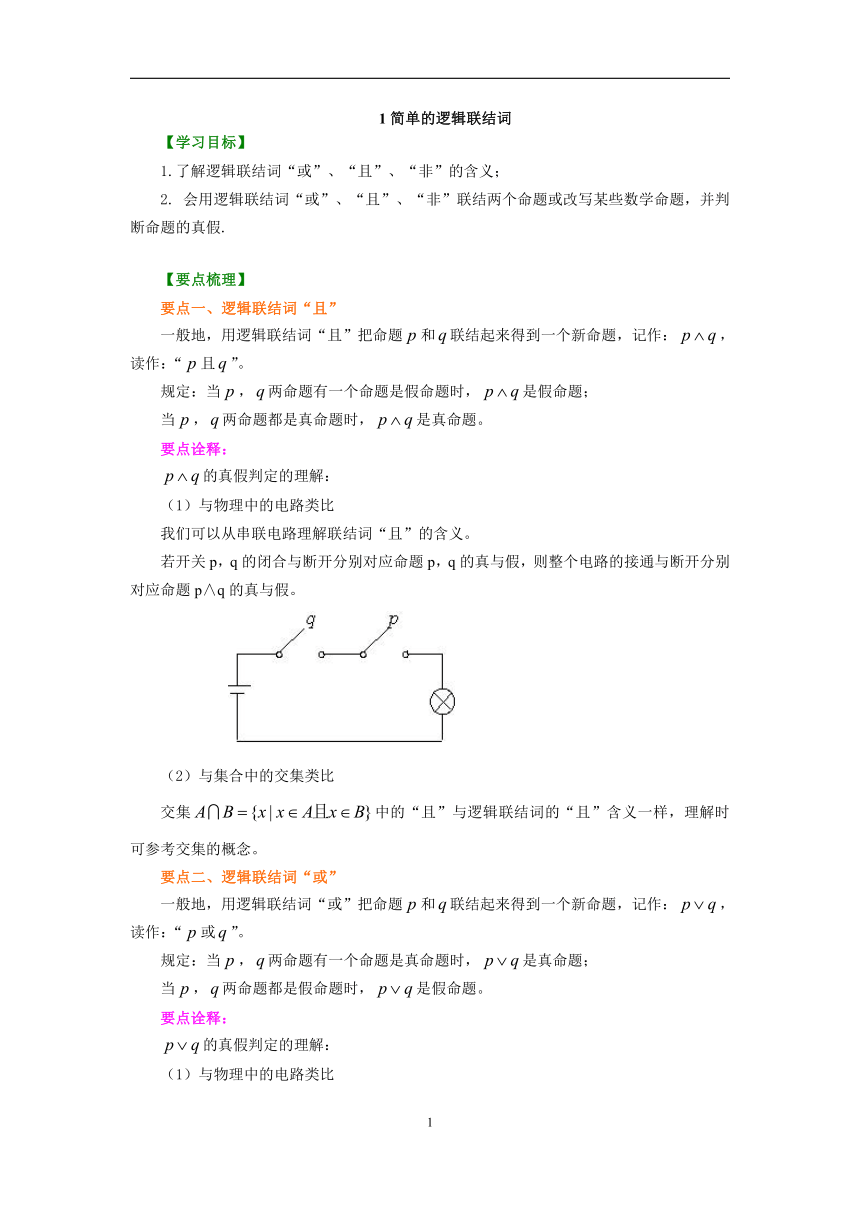
(1)与物理中的电路类比
我们可以从串联电路理解联结词“且”的含义。
若开关p,q的闭合与断开分别对应命题p,q的真与假,则整个电路的接通与断开分别对应命题p∧q的真与假。
(2)与集合中的交集类比
交集中的“且”与逻辑联结词的“且”含义一样,理解时可参考交集的概念。
要点二、逻辑联结词“或”
一般地,用逻辑联结词“或”把命题和联结起来得到一个新命题,记作:,读作:“或”。
规定:当,两命题有一个命题是真命题时,是真命题;
当,两命题都是假命题时,是假命题。
要点诠释:
的真假判定的理解:
(1)与物理中的电路类比
我们可以从并联电路理解联结词“或”的含义。
若开关p,q的闭合与断开对应命题的真与假,则整个电路的接通与断开分别对应命题的p∨q的真与假。
(2)与集合中的并集类比
并集中的“或”与逻辑联结词的“或”含义一样,理解时可参考并集的概念。
(3)“或”有三层含义,以“p或q”为例:
①p成立且q不成立;
②p不成立但q成立;
③p成立且q也成立。
要点三、逻辑联结词“非”
一般地,对一个命题全盘否定得到一个新命题,记作:,读作:“非或的否定”。
规定:当是真命题时,必定是假命题;
当是假命题时,必定是真命题。
要点诠释:
(1)逻辑联结词中的“非”相当于集合中补集的概念,谈到补集必然要说全集,谈论“非”时也应该弄清这件事是在一个什么样的范围中研究。
(2)下面是一些常用词的否定:
是
等于
属于
有
都是
至少
一个
至多
一个
一定
x=1或x=2
x>1且x<3
不是
不等于
不属于
没有
不都是
一个
都没
有
至少
两个
一定不
x≠1且x≠2
x≤1或x≥3
(3)否命题与命题的否定之间的区别:
否命题是对原命题的条件和结论分别做否定后得到的命题(否定二次);命题的否定是只对原命题的结论做否定(否定一次),即.如:
命题: 若,则.
命题的否命题:若,则.
命题的否定即:若,则.
(4)“或”、“且”联结的命题的否定形式:
“p或q”的否定;
“p且q”的否定
要点四、简单命题与复合命题
(1)定义:
简单命题:不含逻辑联结词的命题叫简单命题。
复合命题:由简单命题与逻辑联结词“或”、“且”、“非”构成的命题叫做复合命题。
(2)复合命题的构成形式:
①p或q;记作:
②p且q;记作:
③非p(即命题p的否定);记作:
(3)复合命题的真假判断
真
真
假
真
真
真
假
假
真
假
假
真
真
真
假
假
假
真
假
假
要点诠释:
①当p、q同时为假时,“p或q”为假,其它情况时为真,可简称为“一真必真”;
②当p、q同时为真时,“p且q”为真,其它情况时为假,可简称为“一假必假”。
③“非p”与p的真假相反.
【典型例题】
类型一:复合命题的构成
例1.指出下列复合命题的结构,写出构成其的简单命题.
(1) 菱形的对角线互相垂直平分;
(2) 不是无理数;
(3)6是12或18的约数.
【解析】
(1)且的形式,其中:菱形的对角线互相垂直,:菱形对角线互相平分;
(2)非的形式,其中:是无理数;
(3)或的形式,其中:6是12的约数,:6是18的约数.
【总结升华】正确理解逻辑联结词“或”、“且”、“非”的含义是解题的关键。根据上述各复合命题中出现的逻辑联结词或语句的意义确定复合命题的形式。
举一反三:
【变式1】判断下列复合命题的形式,写出构成其的简单命题
(1)1是奇数或偶数;
(2)梯形不是平行四边形;
(3)2是偶数也是质数.
【答案】
(1)或的形式,其中:1是奇数,:1是偶数;
(2)非的形式,其中:梯形是平行四边形;
(3)且的形式,其中:2是偶数,:2是质数。
例2.判断下列命题中是否含有逻辑联结词“或”、“且”、“非”,若含有,请指出其中p、q的基本命题.
正方形的对角线垂直相等;
2是4和6的约数;
不等式的解集为。
【解析】(1)是“且”形式的命题,其中p:正方形的对角线互相垂直;q:正方形的对角线相等.
(2)是“且”形式的命题,其中p:2是4的约数;q:2是6的约数.
(3)是简单命题,而不是用“或”联结的复合命题
【总结升华】对于用逻辑联结词“或”、“且”、“非”联结的新命题的结构特点不能仅从字面上看它是否含有“或”、“且”、“非”等逻辑联结词,而应从命题的结构来看是否用逻辑联结词联结两个命题.
举一反三:
【变式1】将下列各组命题用“且”联结组成新命题:
(1)p:平行四边形的对角线互相平分,
q:平行四边形的对角线相等;
(2)p:集合A是AB的子集,
q:集合A是AB的子集;
(3)p:,
q:3>4.
【答案】
(1)p∧q:平行四边形的对角线互相平分且相等;
(2)p∧q:集合A是AB的子集,且是AB的子集;
(3)p∧q:,且3>4.
【变式2】分别指出下列复合命题的形式及构成的简单命题。
李明是老师,赵山也是老师;
1是合数或质数;
他是运动员兼教练员;
【答案】
(1)这个命题是“且”形式,其中p:李明是老师,q:赵山是老师。
(2)这个命题是“或”形式,其中p:1是合数,q:1是质数。
(3)这个命题是“且”形式,其中p:他是运动员,q:他是教练员。
例3.已知命题、,写出或、且、非的形式并判断真假。
(1): , :.
(2): , :
【解析】
(1)或:或,即(真命题),
且:且(假命题),
非():(真命题),
(2)或:或,即(真命题),
且:且(假命题),
非():,即(假命题).
【总结升华】 先判断各简单命题的真假,再依据复合命题的构成形式写出复合命题,最后判断复合命题的真假.
举一反三:
【变式1】已知命题、,试写出或、且、非的形式的命题并判断真假.
(1) :平行四边形的一组对边平行,:平行四边形的一组对边相等
(2) :,:
(3) :, :
【答案】
(1)或:平行四边形的一组对边平行或相等(真命题);
且:平行四边形的一组对边平行且相等(真命题);
非:平行四边形的一组对边不平行(假命题)。
(2)或:或,即(真命题)
且:且(假命题)
非:(真命题)
(3)或:或(真命题)
且:且(真命题)
非:(假命题)
【变式2】(2018秋 宣城期末)“a2+b2≠0”的含义为( )
A.a和b都不为0
B.a和b至少有一个为0
C.a和b至少有一个不为0
D.a不为0且b为0,或b不为0且a为0
【答案】
a2+b2≠0的等价条件得a≠0或b≠0,即两者中至少有一个不为0,对照四个选项,只有C与此意思相同,C正确;
A中a和b都不0,是a2+b2≠0的充分不必要条件;
B中a和b至少有一个为0包括了两个数都是0,故不对;
D中只是两个数仅有一个为0,概括不全面,故不对;
故选C。
类型二:复合命题真假的判定
例4. (2018 湖南)已知命题p:若x>y,则-x<-y;命题q:若x>y,则x2>y2,在命题①p∧q;②p∨q;③p∧(¬q);④(¬p)∨q中,真命题是( )
A.①③ B.①④
C.②③ D.②④
【答案】C.
【解析】根据不等式的性质可知,若x>y,则-x<-y成立,即p为真命题,
当x=1,y=-1时,满足x>y,但x2>y2不成立,即命题q为假命题,
则①p∧q为假命题;②p∨q为真命题;③p∧(¬q)为真命题;④(¬p)∨q为假命题,
故选:C.
【总结升华】解答这类逻辑推理问题关键在于充分利用真值表进行分析,也就是由给出复合命题的真假情况,利用真值表逆向思考,从而推断出组成复合命题的简单命题的真值情况,再判断相关命题正确与否.
举一反三:
【变式1】已知命题:
p:对任意x∈R,总有|x|≥0,q:x=1是方程x+2=0的根;则下列命题为真命题的是( )
A. p∧¬q B.¬p∧q C.¬p∧¬q D. p∧q
【答案】根据绝对值的性质可知,对任意x∈R,总有|x|≥0成立,即p为真命题,
当x=1时,x+2=3≠0,即x=1不是方程x+2=0的根,即q为假命题,
则p∧¬q,为真命题,
故选:A.
【变式2】已知命题p:3≥3;q:3>4,则下列判断正确的是( )
A.为真,为真,为假
B.为真,为假,为真
C.为假,为假,为假
D.为真,为假,为假
【答案】D
【变式3】已知命题p:所有有理数都是实数,命题q:正数的对数都是负数,则下列命题为真命题的是( )
(A)(?p)∨q (B) p∧q
(C)(?p)∨(?q) (D)(?p)∧(?q)
【答案】C
类型三:命题的否定与否命题
例5.写出下列命题的否定和否命题,并判定其真假.
(1):在整数范围内,、都是偶数,则是偶数
(2):若且,则.
【解析】
(1) :在整数范围内,、都是偶数,则不是偶数(假命题);
的否命题是:在整数范围内,若、不都是偶数,则不是偶数(假命题);
(2) :若且,则(假命题);
的否命题是:若或,则(假命题).
【总结升华】
①“且”的否定是“或”;“ 、都是偶数"的否定为“、不都是偶数”.
② 命题的否定和否命题是不一样的.
举一反三:
【变式1】写出下列命题的否定和否命题,并判定其真假.
(1):若,则,全为零;
(2):若且,则.
【答案】
(1)的否定:若,则,不全为零(假命题);
的否命题:若,则,不全为零(真命题);
(2)的否定:若且,则(假命题);
的否命题:若或,则(假命题).
【变式2】“”是指 (填出符合条件的所有选项)
A.且 B.或 C.,至少有一个不是0
D.,都不是0 E. ,不都是0
【答案】A、D;
【解析】指,都不是0,即且.
【巩固练习】
一、选择题
1.有下列命题:
①2004年10月1日是国庆节,又是中秋节;②10的倍数一定是5的倍数;③方程x2=1的解x=±1.
其中使用逻辑联结词的命题有( )
A.0个 B.1个
C.2个 D.3个
2.如果原命题的结构是“p且q”的形式,那么否命题的结构形式为( )
A.?p且?q B.?p或?q
C.?p或q D.?q或p
3.若p、q是两个简单命题,“p或q”的否定是真命题,则必有( )
A.p真q真 B.p假q假
C.p真q假 D.p假q真
4.(2018 北京市东城区高三二模数学(理))已知p,q是简单命题,那么“是真命题”是“是真命题”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
5.已知命题p:, 则非p是( )
A. B. 或 C. 且 D.
6.(2018 北京市西城区高三二模数学(文))设命题p:函数在R上为增函数;命题q:函数为奇函数,则下列命题中真命题是( )
A.p∧q B.(┐p)∨q C.(┐p)∧(┐q ) D.p∧(┐q )
二、填空题
7.p:ax+b>0的解集为,q:(x-a)(x-b)<0的解为a8.设命题p:3≥2,q:;则复合命题“p∨q”,“p∧q”中真命题的个数是________.
9.命题p:2不是质数,命题q:是无理数,在命题“p∧q”、命题“p∨q”“?p”“?q”中,假命题是________,真命题是________.
10.已知命题,.由它们构成的“p∨q”“p∧q”和“?p”形式的复合命题中,为真命题的是________.
三、解答题
11. 已知命题p:0不是自然数,q:π是无理数,写出命题“p∨q”,“p∧q”,并判断其真假.
12. 指出下列命题的构成形式(“p∧q”或“p∨q”)及构成它的命题p,q,并判断它们的真假.
(1)5≥3;
(2)(n-1)·n·(n+1)(n∈N*)既能被2整除,也能被3整除;
(3)?是{?}的元素,也是{?}的真子集.
13.写出下列命题的否定:
(1)a、b、c都相等;
(2)y=cosx是偶函数且是周期函数;
(3)(x-2)(x+5)>0.
14. 已知命题p:方程的两根都是实数;q:方程的两根不相等,试写出由这组命题构成的“p或q”“p且q”“非p”形式的复合命题,并指出其真假.
15. 已知命题p:x2-5x+6≥0;命题q:0【答案与解析】
1.【答案】 C
【解析】 ①中有“且”;②中没有;③中的“或”是逻辑联结词.
2.【答案】 B
【解析】 “且”的否定形式为“或”.
3.【答案】 B
【解析】 “p或q”的否定是:“?p且?q”是真命题,则?p、?q都是真命题,故p、q都是假命题.
4.【答案】D
【解析】由“是真命题”得到p是真命题且q也是真命题,因此知?p识假命题,故前者是后者的既不充分也不必要条件。
5.【答案】C
【解析】由知或,非p是:x不属于A且x不属于B,故选C。
6.【答案】 D
【解析】 命题p为真命题,命题q为假命题,故“p∧(?q)”为真命题.
7.【答案】 假
【解析】 命题p与q都是假命题.
8.【答案】 p∨q与p∧q都正确
9.【答案】 “p∧q”“?q” “p∨q”“?p”
【解析】 因为命题p假,命题q真,所以命题“p∧q”假,命题“p∨q”真,“?p”真,“?q”假.
10.【答案】 p∨q
【解析】 ?是任何非空集合的真子集,故p正确,集合与集合之间用“”“?”“=”表示,元素与集合之间用“∈”“?”表示,故q错误.
11. 【解析】 p∧q:0不是自然数且π是无理数.假命题;p∨q:0不是自然数或π是无理数.真命题.
12. 【解析】 (1)此命题为“p或q”的形式,其中,
p:5>3;q:5=3.
此命题为真命题,因为p为真,q为假,所以“p或q”为真命题.
(2)此命题为“p且q”形式的命题,其中,
p:(n-1)·n·(n+1)(n∈N*)能被2整除;
q:(n-1)·n·(n+1)(n∈N*)能被3整除.
此命题为真命题,因为p为真命题,q也是真命题.所以“p且q”为真命题.
(3)此命题为“p且q”的形式,其中,
p:?是{?}的元素;
q:?是{?}的真子集.
此命题为真命题,因为p为真,q也为真,故“p且q”为真命题.
13.【解析】 (1)a、b、c不都相等,也就是说a、b、c中至少有两个不相等.
(2)y=cosx不是偶函数或不是周期函数.
(3)因为(x-2)(x+5)>0表示x<-5或者x>2,
所以它的否定是x≥-5且x≤2,即-5≤x≤2.
另解:(x-2)(x+5)>0的否定是(x-2)(x+5)≤0,
即-5≤x≤2.
14.【解析】 “p或q”的形式:方程的两根都是实数或不相等.
“p且q”的形式:方程的两根都是实数且不相等.
“非p”的形式:方程无实根.
∵Δ=24-24=0,
∴方程有相等的实根,故p真,q假.
∴p或q真,p且q假,非p假.
15. 【解析】 由x2-5x+6≥0得x≥3或x≤2.
∵命题q为假,∴x≤0或x≥4.
则{x|x≥3或x≤2}∩{x|x≤0或x≥4}={x|x≤0或x≥4}.
∴满足条件的实数x的范围为(-∞,0]∪[4,+∞).
【学习目标】
1.了解逻辑联结词“或”、“且”、“非”的含义;
2. 会用逻辑联结词“或”、“且”、“非”联结两个命题或改写某些数学命题,并判断命题的真假.
【要点梳理】
要点一、逻辑联结词“且”
一般地,用逻辑联结词“且”把命题和联结起来得到一个新命题,记作:,读作:“且”。
规定:当,两命题有一个命题是假命题时,是假命题;
当,两命题都是真命题时,是真命题。
要点诠释:
的真假判定的理解:
(1)与物理中的电路类比
我们可以从串联电路理解联结词“且”的含义。
若开关p,q的闭合与断开分别对应命题p,q的真与假,则整个电路的接通与断开分别对应命题p∧q的真与假。
(2)与集合中的交集类比
交集中的“且”与逻辑联结词的“且”含义一样,理解时可参考交集的概念。
要点二、逻辑联结词“或”
一般地,用逻辑联结词“或”把命题和联结起来得到一个新命题,记作:,读作:“或”。
规定:当,两命题有一个命题是真命题时,是真命题;
当,两命题都是假命题时,是假命题。
要点诠释:
的真假判定的理解:
(1)与物理中的电路类比
我们可以从并联电路理解联结词“或”的含义。
若开关p,q的闭合与断开对应命题的真与假,则整个电路的接通与断开分别对应命题的p∨q的真与假。
(2)与集合中的并集类比
并集中的“或”与逻辑联结词的“或”含义一样,理解时可参考并集的概念。
(3)“或”有三层含义,以“p或q”为例:
①p成立且q不成立;
②p不成立但q成立;
③p成立且q也成立。
要点三、逻辑联结词“非”
一般地,对一个命题全盘否定得到一个新命题,记作:,读作:“非或的否定”。
规定:当是真命题时,必定是假命题;
当是假命题时,必定是真命题。
要点诠释:
(1)逻辑联结词中的“非”相当于集合中补集的概念,谈到补集必然要说全集,谈论“非”时也应该弄清这件事是在一个什么样的范围中研究。
(2)下面是一些常用词的否定:
是
等于
属于
有
都是
至少
一个
至多
一个
一定
x=1或x=2
x>1且x<3
不是
不等于
不属于
没有
不都是
一个
都没
有
至少
两个
一定不
x≠1且x≠2
x≤1或x≥3
(3)否命题与命题的否定之间的区别:
否命题是对原命题的条件和结论分别做否定后得到的命题(否定二次);命题的否定是只对原命题的结论做否定(否定一次),即.如:
命题: 若,则.
命题的否命题:若,则.
命题的否定即:若,则.
(4)“或”、“且”联结的命题的否定形式:
“p或q”的否定;
“p且q”的否定
要点四、简单命题与复合命题
(1)定义:
简单命题:不含逻辑联结词的命题叫简单命题。
复合命题:由简单命题与逻辑联结词“或”、“且”、“非”构成的命题叫做复合命题。
(2)复合命题的构成形式:
①p或q;记作:
②p且q;记作:
③非p(即命题p的否定);记作:
(3)复合命题的真假判断
真
真
假
真
真
真
假
假
真
假
假
真
真
真
假
假
假
真
假
假
要点诠释:
①当p、q同时为假时,“p或q”为假,其它情况时为真,可简称为“一真必真”;
②当p、q同时为真时,“p且q”为真,其它情况时为假,可简称为“一假必假”。
③“非p”与p的真假相反.
【典型例题】
类型一:复合命题的构成
例1.指出下列复合命题的结构,写出构成其的简单命题.
(1) 菱形的对角线互相垂直平分;
(2) 不是无理数;
(3)6是12或18的约数.
【解析】
(1)且的形式,其中:菱形的对角线互相垂直,:菱形对角线互相平分;
(2)非的形式,其中:是无理数;
(3)或的形式,其中:6是12的约数,:6是18的约数.
【总结升华】正确理解逻辑联结词“或”、“且”、“非”的含义是解题的关键。根据上述各复合命题中出现的逻辑联结词或语句的意义确定复合命题的形式。
举一反三:
【变式1】判断下列复合命题的形式,写出构成其的简单命题
(1)1是奇数或偶数;
(2)梯形不是平行四边形;
(3)2是偶数也是质数.
【答案】
(1)或的形式,其中:1是奇数,:1是偶数;
(2)非的形式,其中:梯形是平行四边形;
(3)且的形式,其中:2是偶数,:2是质数。
例2.判断下列命题中是否含有逻辑联结词“或”、“且”、“非”,若含有,请指出其中p、q的基本命题.
正方形的对角线垂直相等;
2是4和6的约数;
不等式的解集为。
【解析】(1)是“且”形式的命题,其中p:正方形的对角线互相垂直;q:正方形的对角线相等.
(2)是“且”形式的命题,其中p:2是4的约数;q:2是6的约数.
(3)是简单命题,而不是用“或”联结的复合命题
【总结升华】对于用逻辑联结词“或”、“且”、“非”联结的新命题的结构特点不能仅从字面上看它是否含有“或”、“且”、“非”等逻辑联结词,而应从命题的结构来看是否用逻辑联结词联结两个命题.
举一反三:
【变式1】将下列各组命题用“且”联结组成新命题:
(1)p:平行四边形的对角线互相平分,
q:平行四边形的对角线相等;
(2)p:集合A是AB的子集,
q:集合A是AB的子集;
(3)p:,
q:3>4.
【答案】
(1)p∧q:平行四边形的对角线互相平分且相等;
(2)p∧q:集合A是AB的子集,且是AB的子集;
(3)p∧q:,且3>4.
【变式2】分别指出下列复合命题的形式及构成的简单命题。
李明是老师,赵山也是老师;
1是合数或质数;
他是运动员兼教练员;
【答案】
(1)这个命题是“且”形式,其中p:李明是老师,q:赵山是老师。
(2)这个命题是“或”形式,其中p:1是合数,q:1是质数。
(3)这个命题是“且”形式,其中p:他是运动员,q:他是教练员。
例3.已知命题、,写出或、且、非的形式并判断真假。
(1): , :.
(2): , :
【解析】
(1)或:或,即(真命题),
且:且(假命题),
非():(真命题),
(2)或:或,即(真命题),
且:且(假命题),
非():,即(假命题).
【总结升华】 先判断各简单命题的真假,再依据复合命题的构成形式写出复合命题,最后判断复合命题的真假.
举一反三:
【变式1】已知命题、,试写出或、且、非的形式的命题并判断真假.
(1) :平行四边形的一组对边平行,:平行四边形的一组对边相等
(2) :,:
(3) :, :
【答案】
(1)或:平行四边形的一组对边平行或相等(真命题);
且:平行四边形的一组对边平行且相等(真命题);
非:平行四边形的一组对边不平行(假命题)。
(2)或:或,即(真命题)
且:且(假命题)
非:(真命题)
(3)或:或(真命题)
且:且(真命题)
非:(假命题)
【变式2】(2018秋 宣城期末)“a2+b2≠0”的含义为( )
A.a和b都不为0
B.a和b至少有一个为0
C.a和b至少有一个不为0
D.a不为0且b为0,或b不为0且a为0
【答案】
a2+b2≠0的等价条件得a≠0或b≠0,即两者中至少有一个不为0,对照四个选项,只有C与此意思相同,C正确;
A中a和b都不0,是a2+b2≠0的充分不必要条件;
B中a和b至少有一个为0包括了两个数都是0,故不对;
D中只是两个数仅有一个为0,概括不全面,故不对;
故选C。
类型二:复合命题真假的判定
例4. (2018 湖南)已知命题p:若x>y,则-x<-y;命题q:若x>y,则x2>y2,在命题①p∧q;②p∨q;③p∧(¬q);④(¬p)∨q中,真命题是( )
A.①③ B.①④
C.②③ D.②④
【答案】C.
【解析】根据不等式的性质可知,若x>y,则-x<-y成立,即p为真命题,
当x=1,y=-1时,满足x>y,但x2>y2不成立,即命题q为假命题,
则①p∧q为假命题;②p∨q为真命题;③p∧(¬q)为真命题;④(¬p)∨q为假命题,
故选:C.
【总结升华】解答这类逻辑推理问题关键在于充分利用真值表进行分析,也就是由给出复合命题的真假情况,利用真值表逆向思考,从而推断出组成复合命题的简单命题的真值情况,再判断相关命题正确与否.
举一反三:
【变式1】已知命题:
p:对任意x∈R,总有|x|≥0,q:x=1是方程x+2=0的根;则下列命题为真命题的是( )
A. p∧¬q B.¬p∧q C.¬p∧¬q D. p∧q
【答案】根据绝对值的性质可知,对任意x∈R,总有|x|≥0成立,即p为真命题,
当x=1时,x+2=3≠0,即x=1不是方程x+2=0的根,即q为假命题,
则p∧¬q,为真命题,
故选:A.
【变式2】已知命题p:3≥3;q:3>4,则下列判断正确的是( )
A.为真,为真,为假
B.为真,为假,为真
C.为假,为假,为假
D.为真,为假,为假
【答案】D
【变式3】已知命题p:所有有理数都是实数,命题q:正数的对数都是负数,则下列命题为真命题的是( )
(A)(?p)∨q (B) p∧q
(C)(?p)∨(?q) (D)(?p)∧(?q)
【答案】C
类型三:命题的否定与否命题
例5.写出下列命题的否定和否命题,并判定其真假.
(1):在整数范围内,、都是偶数,则是偶数
(2):若且,则.
【解析】
(1) :在整数范围内,、都是偶数,则不是偶数(假命题);
的否命题是:在整数范围内,若、不都是偶数,则不是偶数(假命题);
(2) :若且,则(假命题);
的否命题是:若或,则(假命题).
【总结升华】
①“且”的否定是“或”;“ 、都是偶数"的否定为“、不都是偶数”.
② 命题的否定和否命题是不一样的.
举一反三:
【变式1】写出下列命题的否定和否命题,并判定其真假.
(1):若,则,全为零;
(2):若且,则.
【答案】
(1)的否定:若,则,不全为零(假命题);
的否命题:若,则,不全为零(真命题);
(2)的否定:若且,则(假命题);
的否命题:若或,则(假命题).
【变式2】“”是指 (填出符合条件的所有选项)
A.且 B.或 C.,至少有一个不是0
D.,都不是0 E. ,不都是0
【答案】A、D;
【解析】指,都不是0,即且.
【巩固练习】
一、选择题
1.有下列命题:
①2004年10月1日是国庆节,又是中秋节;②10的倍数一定是5的倍数;③方程x2=1的解x=±1.
其中使用逻辑联结词的命题有( )
A.0个 B.1个
C.2个 D.3个
2.如果原命题的结构是“p且q”的形式,那么否命题的结构形式为( )
A.?p且?q B.?p或?q
C.?p或q D.?q或p
3.若p、q是两个简单命题,“p或q”的否定是真命题,则必有( )
A.p真q真 B.p假q假
C.p真q假 D.p假q真
4.(2018 北京市东城区高三二模数学(理))已知p,q是简单命题,那么“是真命题”是“是真命题”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
5.已知命题p:, 则非p是( )
A. B. 或 C. 且 D.
6.(2018 北京市西城区高三二模数学(文))设命题p:函数在R上为增函数;命题q:函数为奇函数,则下列命题中真命题是( )
A.p∧q B.(┐p)∨q C.(┐p)∧(┐q ) D.p∧(┐q )
二、填空题
7.p:ax+b>0的解集为,q:(x-a)(x-b)<0的解为a
9.命题p:2不是质数,命题q:是无理数,在命题“p∧q”、命题“p∨q”“?p”“?q”中,假命题是________,真命题是________.
10.已知命题,.由它们构成的“p∨q”“p∧q”和“?p”形式的复合命题中,为真命题的是________.
三、解答题
11. 已知命题p:0不是自然数,q:π是无理数,写出命题“p∨q”,“p∧q”,并判断其真假.
12. 指出下列命题的构成形式(“p∧q”或“p∨q”)及构成它的命题p,q,并判断它们的真假.
(1)5≥3;
(2)(n-1)·n·(n+1)(n∈N*)既能被2整除,也能被3整除;
(3)?是{?}的元素,也是{?}的真子集.
13.写出下列命题的否定:
(1)a、b、c都相等;
(2)y=cosx是偶函数且是周期函数;
(3)(x-2)(x+5)>0.
14. 已知命题p:方程的两根都是实数;q:方程的两根不相等,试写出由这组命题构成的“p或q”“p且q”“非p”形式的复合命题,并指出其真假.
15. 已知命题p:x2-5x+6≥0;命题q:0
1.【答案】 C
【解析】 ①中有“且”;②中没有;③中的“或”是逻辑联结词.
2.【答案】 B
【解析】 “且”的否定形式为“或”.
3.【答案】 B
【解析】 “p或q”的否定是:“?p且?q”是真命题,则?p、?q都是真命题,故p、q都是假命题.
4.【答案】D
【解析】由“是真命题”得到p是真命题且q也是真命题,因此知?p识假命题,故前者是后者的既不充分也不必要条件。
5.【答案】C
【解析】由知或,非p是:x不属于A且x不属于B,故选C。
6.【答案】 D
【解析】 命题p为真命题,命题q为假命题,故“p∧(?q)”为真命题.
7.【答案】 假
【解析】 命题p与q都是假命题.
8.【答案】 p∨q与p∧q都正确
9.【答案】 “p∧q”“?q” “p∨q”“?p”
【解析】 因为命题p假,命题q真,所以命题“p∧q”假,命题“p∨q”真,“?p”真,“?q”假.
10.【答案】 p∨q
【解析】 ?是任何非空集合的真子集,故p正确,集合与集合之间用“”“?”“=”表示,元素与集合之间用“∈”“?”表示,故q错误.
11. 【解析】 p∧q:0不是自然数且π是无理数.假命题;p∨q:0不是自然数或π是无理数.真命题.
12. 【解析】 (1)此命题为“p或q”的形式,其中,
p:5>3;q:5=3.
此命题为真命题,因为p为真,q为假,所以“p或q”为真命题.
(2)此命题为“p且q”形式的命题,其中,
p:(n-1)·n·(n+1)(n∈N*)能被2整除;
q:(n-1)·n·(n+1)(n∈N*)能被3整除.
此命题为真命题,因为p为真命题,q也是真命题.所以“p且q”为真命题.
(3)此命题为“p且q”的形式,其中,
p:?是{?}的元素;
q:?是{?}的真子集.
此命题为真命题,因为p为真,q也为真,故“p且q”为真命题.
13.【解析】 (1)a、b、c不都相等,也就是说a、b、c中至少有两个不相等.
(2)y=cosx不是偶函数或不是周期函数.
(3)因为(x-2)(x+5)>0表示x<-5或者x>2,
所以它的否定是x≥-5且x≤2,即-5≤x≤2.
另解:(x-2)(x+5)>0的否定是(x-2)(x+5)≤0,
即-5≤x≤2.
14.【解析】 “p或q”的形式:方程的两根都是实数或不相等.
“p且q”的形式:方程的两根都是实数且不相等.
“非p”的形式:方程无实根.
∵Δ=24-24=0,
∴方程有相等的实根,故p真,q假.
∴p或q真,p且q假,非p假.
15. 【解析】 由x2-5x+6≥0得x≥3或x≤2.
∵命题q为假,∴x≤0或x≥4.
则{x|x≥3或x≤2}∩{x|x≤0或x≥4}={x|x≤0或x≥4}.
∴满足条件的实数x的范围为(-∞,0]∪[4,+∞).
