人教版高中数学文科选修1-1同步练习题、期中、期末复习资料、补习资料:14【基础】椭圆综合(文)
文档属性
| 名称 | 人教版高中数学文科选修1-1同步练习题、期中、期末复习资料、补习资料:14【基础】椭圆综合(文) |
|
|
| 格式 | zip | ||
| 文件大小 | 414.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-18 11:42:26 | ||
图片预览





文档简介
椭圆综合
【学习目标】
1.能正熟练使用直接法、待定系数法、定义法求椭圆的方程;
2.能熟练运用几何性质(如范围、对称性、顶点、离心率)解决相关问题;
3.能够把直线与椭圆的位置关系的问题转化为方程组解的问题,判断位置关系及解决相关问题.
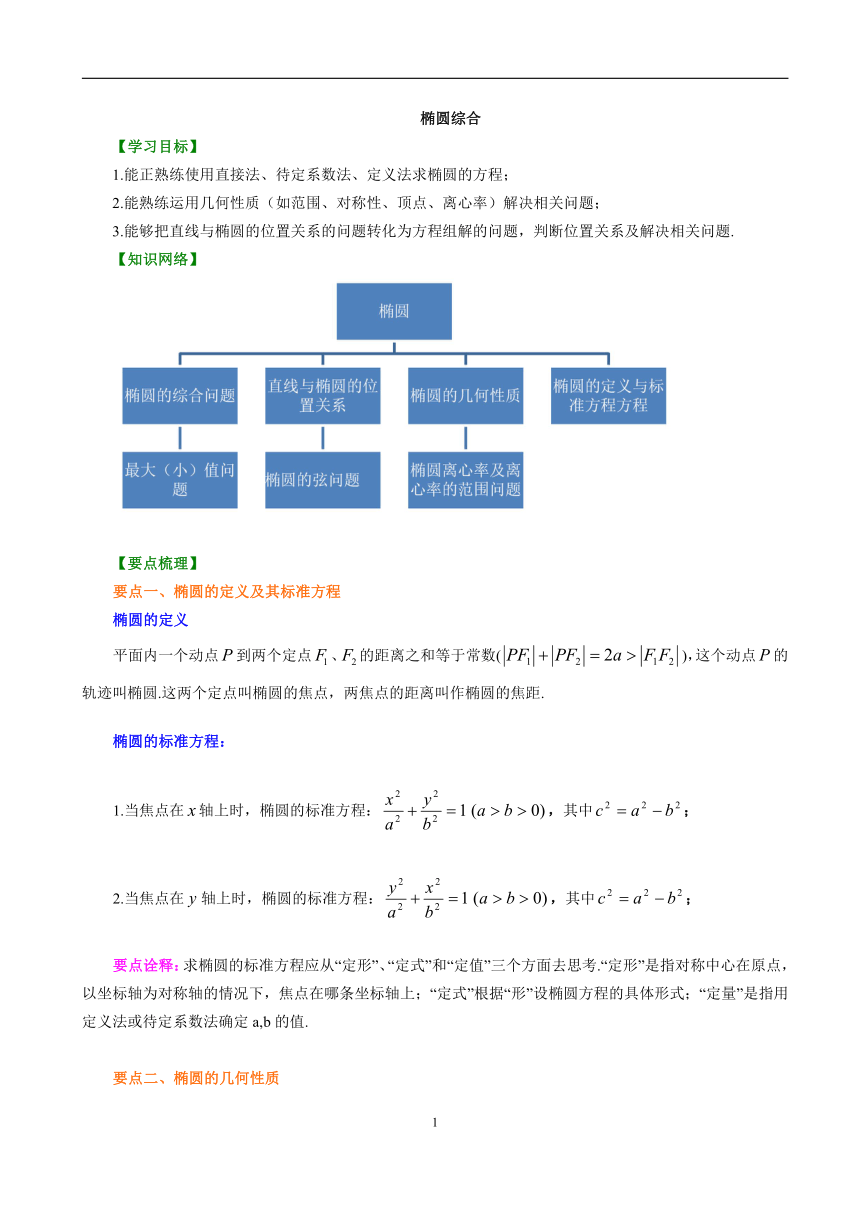
【知识网络】
【要点梳理】
要点一、椭圆的定义及其标准方程
椭圆的定义
平面内一个动点到两个定点、的距离之和等于常数(),这个动点的轨迹叫椭圆.这两个定点叫椭圆的焦点,两焦点的距离叫作椭圆的焦距.
椭圆的标准方程:
1.当焦点在轴上时,椭圆的标准方程:,其中;
2.当焦点在轴上时,椭圆的标准方程:,其中;
要点诠释:求椭圆的标准方程应从“定形”、“定式”和“定值”三个方面去思考.“定形”是指对称中心在原点,以坐标轴为对称轴的情况下,焦点在哪条坐标轴上;“定式”根据“形”设椭圆方程的具体形式;“定量”是指用定义法或待定系数法确定a,b的值.
要点二、椭圆的几何性质
焦点在x轴上
焦点在y轴上
标准方程
图形
性质
焦点
,
,
焦距
范围
,
,
对称性
关于x轴、y轴和原点对称
顶点
,
,
轴
长轴长=,短轴长=
离心率
要点三、直线与椭圆的位置关系
直线与椭圆的位置关系
将直线的方程与椭圆的方程联立成方程组,消元转化为关于x或y的一元二次方程,其判别式为Δ.
①Δ>0直线和椭圆相交直线和椭圆有两个交点(或两个公共点);
②Δ=0直线和椭圆相切直线和椭圆有一个切点(或一个公共点);
③Δ<0直线和椭圆相离直线和椭圆无公共点.
直线与椭圆的相交弦
设直线交椭圆于点两点,则
==
同理可得
这里的求法通常使用韦达定理,需作以下变形:
椭圆的中点弦问题
遇到中点弦问题常用“韦达定理”或“点差法”求解.
在椭圆中,以为中点的弦所在直线的斜率;
涉及弦长的中点问题,常用“点差法”设而不求,将弦所在直线的斜率、弦的中点坐标联系起来相互转化,同时还应充分挖掘题目的隐含条件,寻找量与量间的关系灵活转化,往往就能事半功倍.
解题的主要规律可以概括为“联立方程求交点,韦达定理求弦长,根的分布找范围,曲线定义不能忘”.
【典型例题】
例1.若方程表示焦点在y轴上的椭圆,则m的取值范围是( )
A. B. C. D.
【答案】D
【解析】由题知所以,选D
【总结升华】椭圆的方程要注意焦点轴的不同,标准方程的形式不同,另外要注意对应的a,b,c的不同
举一反三:
【变式1】(2018 江西校级一模)已知椭圆G的中心在坐标原点,长轴在x轴上,离心率为,且椭圆G上一点到其两个焦点的距离之和为12,则椭圆G的方程为( )
A. B.
C. D.
【答案】A
【变式2】已知椭圆过两点求椭圆的标准方程.
【答案】设椭圆的方程为因为在椭圆上
所以有 解得
所以所求椭圆方程为
例2. 已知方程表示椭圆,求的取值范围.
【解析】由得,且.
∴满足条件的的取值范围是,且.
【总结升华】本题易出现如下错解:由得,故的取值范围是.出错的原因是没有注意椭圆的标准方程中这个条件,当时,并不表示椭圆.
举一反三:
【变式】已知椭圆的方程为,焦点在x轴上,则m的取值范围是( )
A.-4≤m≤4 B.-4C.m>4或m<-4 D.0【答案】B
例3 . 若△ABC的两个焦点坐标为A(-4,0)、B(4,0),△ABC的周长为18,则顶点C的轨迹方程为( )
A.
B. (y≠0)
C. (y≠0)
D. (y≠0)
【答案】 D
【解析】 |AB|=8,|AC|+|BC|=10>|AB|,故点C轨迹为椭圆且两焦点为A、B,又因为C点的纵坐标不能为零,所以选D.
【总结升华】本题是先根据椭圆的定义,判定轨迹是椭圆,然后根据椭圆的标准方程,求轨迹的方程.这是求轨迹方程的一种重要思想方法.
举一反三:
【变式】的底边,和两边上中线长之和为30,求此三角形重心的轨迹和顶点的轨迹.
【答案】
(1)以所在的直线为轴,中点为原点建立直角坐标系.设点坐标为,由,知点的轨迹是以、为焦点的椭圆,且除去轴上两点.因,,有,故其方程为.
(2)设,,则. ①
由题意有代入①,得的轨迹方程为,其轨迹是椭圆(除去轴上两点).
类型二:直线与椭圆的位置关系
例4.椭圆ax2+by2=1与直线x+y-1=0相交于A、B,C是AB的中点,若|AB|=,OC的斜率为,求椭圆的方程.
【解析】 由得(a+b)x2-2bx+b-1=0.
设A(x1,y1)、B(x2,y2),
则
.
∵,∴.①
设C(x,y),则,,
∵OC的斜率为,∴.
代入①,得,.
∴椭圆方程为.
【总结升华】处理有关直线与椭圆的位置关系问题及有关弦长问题,采用的方法与处理直线和圆的有所区别;方程的思想是解决这类问题的通法
举一反三:
【变式1】(2018 沂州校级四模)设椭圆的左右焦点分别为F1、F2,点P(a,b)满足| F1F2|=| PF2|,设直线PF2与椭圆交于M,N两点,若|MN|=16,则椭圆的方程为( )
A. B.
C. D.
【答案】B
【解析】因为点P(a,b)满足| F1F2|=| PF2|,所以
整理得,得
所以,可得椭圆方程为
直线PF2的方程为,
代入椭圆方程,消去y并整理,得解得或
得
所以
所以c=5,
所以椭圆方程为,故选:B。
【变式2】已知椭圆C的左、右焦点坐标分别是(,0),(,0),离心率是,直经y=t与椭圆C交于不同的两点M、N,以线段MN为直径作圆P,圆心为P.
(1)求椭圆C的方程;
(2)若圆P与x轴相切,求圆心P的坐标.
【答案】 (1)∵且,∴,b=1.
∴椭圆c的方程为.
(2)由题意知点P(0,t)(-1由得
∴圆P的半径为,
又∵圆P与x轴相切,
∴,解得,
故P点坐标为.
类型三:椭圆中的最值问题
例5 . AB为过椭圆中心的弦,F(c,0)为椭圆的左焦点,则△AFB的面积最大值是( )
A.b2 B.bc
C.ab D.ac
【答案】 B
【解析】 S△ABF=S△AOF+S△BOF=|OF|·|yA-yB|,
当A、B为短轴两个端点时,|yA-yB|最大,最大值为2b.
∴△ABF面积的最大值为bc.
【总结升华】椭圆中的最值问题往往要多结合图形的特征,或是设出有关变量利用函数思想解决.
举一反三:
【变式】设P是椭圆短轴的一个端点,Q为椭圆上的一个动点,求的最大值
【答案】依题意可设,则
∵Q在椭圆上
∴
=
=
∵则
当时,去最大值
若,则当时,取最大值2.
【巩固练习】
选择题
1.设定点F1(0,-3),F2(0,3),动点P(x,y)满足条件|PF1|+|PF2|=a(a>0),则动点P的轨迹是( )
A.椭圆
B.线段
C.椭圆、线段或不存在
D.不存在
2.椭圆2x2+3y2=12的两焦点之间的距离是( )
A. B. C. D.
3.(2018 河北区模拟)若焦点在x轴上的椭圆的离心率为,则m=( )
A. B. C. D.
4.以椭圆两焦点F1、F2所连线段为直径的圆,恰好过短轴两端点,则此椭圆的离心率e等于( )
A. B. C. D.
5. 过椭圆的一个焦点的直线与椭圆交于、两点,则、与椭圆的另一焦点构成,那么的周长是( )
A. B. 2 C. D. 1
6. 已知椭圆两焦点为F1(-4,0)、F2(4,0),P在椭圆上,且△PF1F2的最大面积是12,则椭圆方程是( )
A. B.
C. D.
二、填空题
7.(2018 珠海二模改编)已知B(-2,0),C(2,0),A为动点,的周长为10,则动点A的满足的方程为___________.
8.在△ABC中,∠A=90°,tanB=.若以A、B为焦点的椭圆经过点C,则该椭圆的离心率e=_________.
9.设是椭圆上的一点,是椭圆的两个焦点,则的最大值为 .
10.若过椭圆内一点(2,1)的弦被该点平分,则该弦所在直线的方程是______________.
三、解答题
11.已知椭圆x2+(m+3)y2=m(m>0)的离心率,求m的值及椭圆的长轴和短轴的长、焦点坐标、顶点坐标.
12.已知椭圆的中心在原点,它在x轴上的一个焦点F与短轴的两个端点B1,B2的连线互相垂直,且这个焦点与较近的长轴的端点A的距离为,求这个椭圆的方程.
13. 已知F1、F2是椭圆的两个焦点,P是椭圆上任一点,若∠F1PF2=,求△F1PF2的面积.
14.求以椭圆9x2+5y2=45的焦点为焦点,且经过点M(2,)的椭圆的标准方程.
15. 已知一直线与椭圆交于A、B两点.
(1)若弦AB的段中点坐标为,求直线AB的方程;
(2)若直线AB的斜率为2,求弦AB的中点M的轨迹方程.
16.(2018 安徽文)设椭圆E的方程为,点O为坐标原点,点A的坐标为(a,0),点B的坐标为(0,b),点M在线段AB上,满足|BM|=2|MA|,直线OM的斜率为。
(1)求E的离心率e;
(2)设点C的坐标为(0,-b),N为线段AC的中点,证明:MNAB.
【答案与解析】
1. 答案: C
解析: 当a>|F1F2|=6时,动点P的轨迹为椭圆;
当a=|F1F2|=6时,动点P的轨迹为线段;
当a<|F1F2|=6时,动点P的轨迹不存在.
2. 答案:D
解析: 椭圆方程2x2+3y2=12可化为:,
a2=6,b2=4,c2=6-4=2,∴2c=.
3.答案:A
解析:由题意,则,化简后得,故选A.
4. 答案: B
解析: 由题意得b=c,∴a2=b2+c2=2c2,
∴.
5.答案:A
解析:由椭圆的定义知∴的周长为
6. 答案: C
解析: 由题意得c=4,∵P在椭圆上,且△PF1F2的最大面积为12,
∴,即bc=12,
∴b=3,a=5,故椭圆方程为.
7.答案:
解析:
点A的轨迹是以B,C为焦点的椭圆(除去B、C),且2a=6,c=2,
顶点A的轨迹方程为。
8.答案:
解析:设|AC|=3x,|AB|=4x,
又∵∠A=90°,∴|BC|=5x.
由椭圆定义知|AC|+|BC|=2a=8x,
那么2c=|AB|=4x,
∴.
9.答案:
解析:由均值不等式得,
10.答案: x+2y-4=0
解析:设弦两端点A(x1,y1),B(x2,y2),则,,两式相减并把x1+x2=4,y1+y2=2代入得,,
∴所求直线方程为y-1=- (x-2),
即x+2y-4=0.
11. 解析: 椭圆方程可化为,
∵,
∴.
即a2=m,,.
由得,,∴m=1.
∴椭圆的标准方程为,
∴a=1,,.
∴椭圆的长轴长为2,短轴长为1;两焦点坐标分别为,;四个顶点分别为A1(-1,0),A2(1,0),B1(0,),B2(0,).
12.解析:由于椭圆中心在原点,焦点在x轴上,可设其方程为(a>b>0).
由椭圆的对称性知,|B1F|=|B2F|,又B1F⊥B2F,因此△B1FB2为等腰直角三角形,于是|OB2|=|OF|,即b=c.
又即,且a2+b2=c2.
将以上三式联立,得方程组,
解得
所求椭圆方程是.
13.解析: 设|PF1|=m,|PF2|=n.
根据椭圆定义有m+n=20,
又,∴在△F1PF2中,
由余弦定理得m2+n2-2mncos=122,
∴m2+n2-mn=144,∴(m+n)2-3mn=144,
∴,
∴S△F1PF2=|PF1||PF2|sin∠F1PF2
.
14.解析:由9x2+5y2=45,得.
其焦点F1(0,2)、F2(0,-2).
设所求椭圆方程为.
又∵点在椭圆上,∴ ①
又a2-b2=4②
解①②得a2=12,b2=8.
故所求椭圆方程为.
15. 解析:
(1)设点,,则
,,,,
∴,即,
∴,
∴直线AB的方程为.
(2)设直线AB的方程为,代入椭圆方程
消去,得,
∴,解得,
∵,
∴弦AB的中点M:,
消去参数,得,
故弦AB的中点M的轨迹方程:().
16. 解析:
(Ⅰ) ∵ |BM|=2|MA|且A(a,0),B(0,b)
∴
又∵ OM的斜率为
∴
(Ⅱ)由题意可知N点的坐标为
∴
∴
∴ MN⊥AB
【学习目标】
1.能正熟练使用直接法、待定系数法、定义法求椭圆的方程;
2.能熟练运用几何性质(如范围、对称性、顶点、离心率)解决相关问题;
3.能够把直线与椭圆的位置关系的问题转化为方程组解的问题,判断位置关系及解决相关问题.
【知识网络】
【要点梳理】
要点一、椭圆的定义及其标准方程
椭圆的定义
平面内一个动点到两个定点、的距离之和等于常数(),这个动点的轨迹叫椭圆.这两个定点叫椭圆的焦点,两焦点的距离叫作椭圆的焦距.
椭圆的标准方程:
1.当焦点在轴上时,椭圆的标准方程:,其中;
2.当焦点在轴上时,椭圆的标准方程:,其中;
要点诠释:求椭圆的标准方程应从“定形”、“定式”和“定值”三个方面去思考.“定形”是指对称中心在原点,以坐标轴为对称轴的情况下,焦点在哪条坐标轴上;“定式”根据“形”设椭圆方程的具体形式;“定量”是指用定义法或待定系数法确定a,b的值.
要点二、椭圆的几何性质
焦点在x轴上
焦点在y轴上
标准方程
图形
性质
焦点
,
,
焦距
范围
,
,
对称性
关于x轴、y轴和原点对称
顶点
,
,
轴
长轴长=,短轴长=
离心率
要点三、直线与椭圆的位置关系
直线与椭圆的位置关系
将直线的方程与椭圆的方程联立成方程组,消元转化为关于x或y的一元二次方程,其判别式为Δ.
①Δ>0直线和椭圆相交直线和椭圆有两个交点(或两个公共点);
②Δ=0直线和椭圆相切直线和椭圆有一个切点(或一个公共点);
③Δ<0直线和椭圆相离直线和椭圆无公共点.
直线与椭圆的相交弦
设直线交椭圆于点两点,则
==
同理可得
这里的求法通常使用韦达定理,需作以下变形:
椭圆的中点弦问题
遇到中点弦问题常用“韦达定理”或“点差法”求解.
在椭圆中,以为中点的弦所在直线的斜率;
涉及弦长的中点问题,常用“点差法”设而不求,将弦所在直线的斜率、弦的中点坐标联系起来相互转化,同时还应充分挖掘题目的隐含条件,寻找量与量间的关系灵活转化,往往就能事半功倍.
解题的主要规律可以概括为“联立方程求交点,韦达定理求弦长,根的分布找范围,曲线定义不能忘”.
【典型例题】
例1.若方程表示焦点在y轴上的椭圆,则m的取值范围是( )
A. B. C. D.
【答案】D
【解析】由题知所以,选D
【总结升华】椭圆的方程要注意焦点轴的不同,标准方程的形式不同,另外要注意对应的a,b,c的不同
举一反三:
【变式1】(2018 江西校级一模)已知椭圆G的中心在坐标原点,长轴在x轴上,离心率为,且椭圆G上一点到其两个焦点的距离之和为12,则椭圆G的方程为( )
A. B.
C. D.
【答案】A
【变式2】已知椭圆过两点求椭圆的标准方程.
【答案】设椭圆的方程为因为在椭圆上
所以有 解得
所以所求椭圆方程为
例2. 已知方程表示椭圆,求的取值范围.
【解析】由得,且.
∴满足条件的的取值范围是,且.
【总结升华】本题易出现如下错解:由得,故的取值范围是.出错的原因是没有注意椭圆的标准方程中这个条件,当时,并不表示椭圆.
举一反三:
【变式】已知椭圆的方程为,焦点在x轴上,则m的取值范围是( )
A.-4≤m≤4 B.-4
例3 . 若△ABC的两个焦点坐标为A(-4,0)、B(4,0),△ABC的周长为18,则顶点C的轨迹方程为( )
A.
B. (y≠0)
C. (y≠0)
D. (y≠0)
【答案】 D
【解析】 |AB|=8,|AC|+|BC|=10>|AB|,故点C轨迹为椭圆且两焦点为A、B,又因为C点的纵坐标不能为零,所以选D.
【总结升华】本题是先根据椭圆的定义,判定轨迹是椭圆,然后根据椭圆的标准方程,求轨迹的方程.这是求轨迹方程的一种重要思想方法.
举一反三:
【变式】的底边,和两边上中线长之和为30,求此三角形重心的轨迹和顶点的轨迹.
【答案】
(1)以所在的直线为轴,中点为原点建立直角坐标系.设点坐标为,由,知点的轨迹是以、为焦点的椭圆,且除去轴上两点.因,,有,故其方程为.
(2)设,,则. ①
由题意有代入①,得的轨迹方程为,其轨迹是椭圆(除去轴上两点).
类型二:直线与椭圆的位置关系
例4.椭圆ax2+by2=1与直线x+y-1=0相交于A、B,C是AB的中点,若|AB|=,OC的斜率为,求椭圆的方程.
【解析】 由得(a+b)x2-2bx+b-1=0.
设A(x1,y1)、B(x2,y2),
则
.
∵,∴.①
设C(x,y),则,,
∵OC的斜率为,∴.
代入①,得,.
∴椭圆方程为.
【总结升华】处理有关直线与椭圆的位置关系问题及有关弦长问题,采用的方法与处理直线和圆的有所区别;方程的思想是解决这类问题的通法
举一反三:
【变式1】(2018 沂州校级四模)设椭圆的左右焦点分别为F1、F2,点P(a,b)满足| F1F2|=| PF2|,设直线PF2与椭圆交于M,N两点,若|MN|=16,则椭圆的方程为( )
A. B.
C. D.
【答案】B
【解析】因为点P(a,b)满足| F1F2|=| PF2|,所以
整理得,得
所以,可得椭圆方程为
直线PF2的方程为,
代入椭圆方程,消去y并整理,得解得或
得
所以
所以c=5,
所以椭圆方程为,故选:B。
【变式2】已知椭圆C的左、右焦点坐标分别是(,0),(,0),离心率是,直经y=t与椭圆C交于不同的两点M、N,以线段MN为直径作圆P,圆心为P.
(1)求椭圆C的方程;
(2)若圆P与x轴相切,求圆心P的坐标.
【答案】 (1)∵且,∴,b=1.
∴椭圆c的方程为.
(2)由题意知点P(0,t)(-1
∴圆P的半径为,
又∵圆P与x轴相切,
∴,解得,
故P点坐标为.
类型三:椭圆中的最值问题
例5 . AB为过椭圆中心的弦,F(c,0)为椭圆的左焦点,则△AFB的面积最大值是( )
A.b2 B.bc
C.ab D.ac
【答案】 B
【解析】 S△ABF=S△AOF+S△BOF=|OF|·|yA-yB|,
当A、B为短轴两个端点时,|yA-yB|最大,最大值为2b.
∴△ABF面积的最大值为bc.
【总结升华】椭圆中的最值问题往往要多结合图形的特征,或是设出有关变量利用函数思想解决.
举一反三:
【变式】设P是椭圆短轴的一个端点,Q为椭圆上的一个动点,求的最大值
【答案】依题意可设,则
∵Q在椭圆上
∴
=
=
∵则
当时,去最大值
若,则当时,取最大值2.
【巩固练习】
选择题
1.设定点F1(0,-3),F2(0,3),动点P(x,y)满足条件|PF1|+|PF2|=a(a>0),则动点P的轨迹是( )
A.椭圆
B.线段
C.椭圆、线段或不存在
D.不存在
2.椭圆2x2+3y2=12的两焦点之间的距离是( )
A. B. C. D.
3.(2018 河北区模拟)若焦点在x轴上的椭圆的离心率为,则m=( )
A. B. C. D.
4.以椭圆两焦点F1、F2所连线段为直径的圆,恰好过短轴两端点,则此椭圆的离心率e等于( )
A. B. C. D.
5. 过椭圆的一个焦点的直线与椭圆交于、两点,则、与椭圆的另一焦点构成,那么的周长是( )
A. B. 2 C. D. 1
6. 已知椭圆两焦点为F1(-4,0)、F2(4,0),P在椭圆上,且△PF1F2的最大面积是12,则椭圆方程是( )
A. B.
C. D.
二、填空题
7.(2018 珠海二模改编)已知B(-2,0),C(2,0),A为动点,的周长为10,则动点A的满足的方程为___________.
8.在△ABC中,∠A=90°,tanB=.若以A、B为焦点的椭圆经过点C,则该椭圆的离心率e=_________.
9.设是椭圆上的一点,是椭圆的两个焦点,则的最大值为 .
10.若过椭圆内一点(2,1)的弦被该点平分,则该弦所在直线的方程是______________.
三、解答题
11.已知椭圆x2+(m+3)y2=m(m>0)的离心率,求m的值及椭圆的长轴和短轴的长、焦点坐标、顶点坐标.
12.已知椭圆的中心在原点,它在x轴上的一个焦点F与短轴的两个端点B1,B2的连线互相垂直,且这个焦点与较近的长轴的端点A的距离为,求这个椭圆的方程.
13. 已知F1、F2是椭圆的两个焦点,P是椭圆上任一点,若∠F1PF2=,求△F1PF2的面积.
14.求以椭圆9x2+5y2=45的焦点为焦点,且经过点M(2,)的椭圆的标准方程.
15. 已知一直线与椭圆交于A、B两点.
(1)若弦AB的段中点坐标为,求直线AB的方程;
(2)若直线AB的斜率为2,求弦AB的中点M的轨迹方程.
16.(2018 安徽文)设椭圆E的方程为,点O为坐标原点,点A的坐标为(a,0),点B的坐标为(0,b),点M在线段AB上,满足|BM|=2|MA|,直线OM的斜率为。
(1)求E的离心率e;
(2)设点C的坐标为(0,-b),N为线段AC的中点,证明:MNAB.
【答案与解析】
1. 答案: C
解析: 当a>|F1F2|=6时,动点P的轨迹为椭圆;
当a=|F1F2|=6时,动点P的轨迹为线段;
当a<|F1F2|=6时,动点P的轨迹不存在.
2. 答案:D
解析: 椭圆方程2x2+3y2=12可化为:,
a2=6,b2=4,c2=6-4=2,∴2c=.
3.答案:A
解析:由题意,则,化简后得,故选A.
4. 答案: B
解析: 由题意得b=c,∴a2=b2+c2=2c2,
∴.
5.答案:A
解析:由椭圆的定义知∴的周长为
6. 答案: C
解析: 由题意得c=4,∵P在椭圆上,且△PF1F2的最大面积为12,
∴,即bc=12,
∴b=3,a=5,故椭圆方程为.
7.答案:
解析:
点A的轨迹是以B,C为焦点的椭圆(除去B、C),且2a=6,c=2,
顶点A的轨迹方程为。
8.答案:
解析:设|AC|=3x,|AB|=4x,
又∵∠A=90°,∴|BC|=5x.
由椭圆定义知|AC|+|BC|=2a=8x,
那么2c=|AB|=4x,
∴.
9.答案:
解析:由均值不等式得,
10.答案: x+2y-4=0
解析:设弦两端点A(x1,y1),B(x2,y2),则,,两式相减并把x1+x2=4,y1+y2=2代入得,,
∴所求直线方程为y-1=- (x-2),
即x+2y-4=0.
11. 解析: 椭圆方程可化为,
∵,
∴.
即a2=m,,.
由得,,∴m=1.
∴椭圆的标准方程为,
∴a=1,,.
∴椭圆的长轴长为2,短轴长为1;两焦点坐标分别为,;四个顶点分别为A1(-1,0),A2(1,0),B1(0,),B2(0,).
12.解析:由于椭圆中心在原点,焦点在x轴上,可设其方程为(a>b>0).
由椭圆的对称性知,|B1F|=|B2F|,又B1F⊥B2F,因此△B1FB2为等腰直角三角形,于是|OB2|=|OF|,即b=c.
又即,且a2+b2=c2.
将以上三式联立,得方程组,
解得
所求椭圆方程是.
13.解析: 设|PF1|=m,|PF2|=n.
根据椭圆定义有m+n=20,
又,∴在△F1PF2中,
由余弦定理得m2+n2-2mncos=122,
∴m2+n2-mn=144,∴(m+n)2-3mn=144,
∴,
∴S△F1PF2=|PF1||PF2|sin∠F1PF2
.
14.解析:由9x2+5y2=45,得.
其焦点F1(0,2)、F2(0,-2).
设所求椭圆方程为.
又∵点在椭圆上,∴ ①
又a2-b2=4②
解①②得a2=12,b2=8.
故所求椭圆方程为.
15. 解析:
(1)设点,,则
,,,,
∴,即,
∴,
∴直线AB的方程为.
(2)设直线AB的方程为,代入椭圆方程
消去,得,
∴,解得,
∵,
∴弦AB的中点M:,
消去参数,得,
故弦AB的中点M的轨迹方程:().
16. 解析:
(Ⅰ) ∵ |BM|=2|MA|且A(a,0),B(0,b)
∴
又∵ OM的斜率为
∴
(Ⅱ)由题意可知N点的坐标为
∴
∴
∴ MN⊥AB
