人教版高中数学文科选修1-1同步练习题、期中、期末复习资料、补习资料:21【基础】直线与双曲线的位置关系(文)
文档属性
| 名称 | 人教版高中数学文科选修1-1同步练习题、期中、期末复习资料、补习资料:21【基础】直线与双曲线的位置关系(文) |
|
|
| 格式 | zip | ||
| 文件大小 | 470.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-18 11:51:18 | ||
图片预览




文档简介
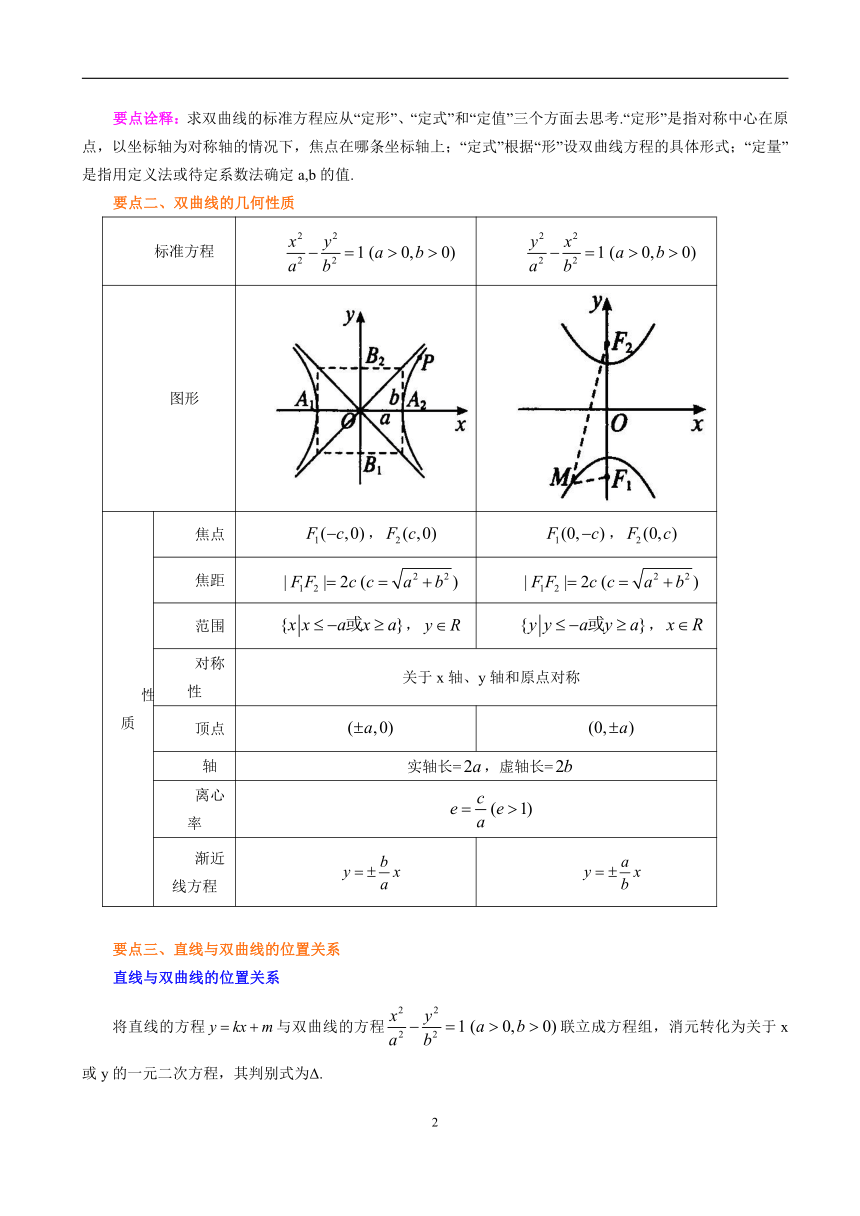
直线与双曲线的位置关系
【学习目标】
1.能正熟练使用直接法、待定系数法、定义法求双曲线的方程;
2.能熟练运用几何性质(如范围、对称性、顶点、离心率、渐近线)解决相关问题;
3.能够把直线与双曲线的位置关系的问题转化为方程组解的问题,判断位置关系及解决相关问题.
【知识网络】
【要点梳理】
要点一、双曲线的定义及其标准方程
双曲线的定义
在平面内,到两个定点、的距离之差的绝对值等于常数(大于0且)的动点的轨迹叫作双曲线.这两个定点、叫双曲线的焦点,两焦点的距离叫作双曲线的焦距.
双曲线的标准方程:
焦点在x轴上的双曲线的标准方程
说明:焦点是F1(-c,0)、F2(c,0),其中c2=a2-b2
焦点在y轴上的双曲线的标准方程
说明:焦点是F1(0,-c)、F2(0,c),其中c2=a2-b2
要点诠释:求双曲线的标准方程应从“定形”、“定式”和“定值”三个方面去思考.“定形”是指对称中心在原点,以坐标轴为对称轴的情况下,焦点在哪条坐标轴上;“定式”根据“形”设双曲线方程的具体形式;“定量”是指用定义法或待定系数法确定a,b的值.
要点二、双曲线的几何性质
标准方程
图形
性质
焦点
,
,
焦距
范围
,
,
对称性
关于x轴、y轴和原点对称
顶点
轴
实轴长=,虚轴长=
离心率
渐近线方程
要点三、直线与双曲线的位置关系
直线与双曲线的位置关系
将直线的方程与双曲线的方程联立成方程组,消元转化为关于x或y的一元二次方程,其判别式为Δ.
若即,直线与双曲线渐近线平行,直线与双曲线相交与一点;
若即,
①Δ>0直线和双曲线相交直线和双曲线相交,有两个交点;
②Δ=0直线和双曲线相切直线和双曲线相切,有一个公共点;
③Δ<0直线和双曲线相离直线和双曲线相离,无公共点.
直线与双曲线的相交弦
设直线交双曲线于点两点,则
==
同理可得
这里的求法通常使用韦达定理,需作以下变形:
双曲线的中点弦问题
遇到中点弦问题常用“韦达定理”或“点差法”求解.
在双曲线中,以为中点的弦所在直线的斜率;
涉及弦长的中点问题,常用“点差法”设而不求,将弦所在直线的斜率、弦的中点坐标联系起来相互转化,同时还应充分挖掘题目的隐含条件,寻找量与量间的关系灵活转化,往往就能事半功倍.
解题的主要规律可以概括为“联立方程求交点,韦达定理求弦长,根的分布找范围,曲线定义不能忘”.
要点四、双曲线的实际应用与最值问题
对于双曲线的实际应用问题,我们要抽象出相应的数学问题,即建立数学模型,一般要先建立直角坐标系,然后利用双曲线定义,构建参数a,b,c之间的关系,得到双曲线方程,利用方程求解
双曲线中的最值问题,按照转化途径主要有以下三种:
利用定义转化
利用双曲线的几何性质
转化为函数求最值
【典型例题】
类型一:双曲线的方程与性质
例1.求下列双曲线的标准方程.
(1)与椭圆共焦点,且过点(-2,)的双曲线;
(2)与双曲线有公共焦点,且过点(3,2)的双曲线.
【解析】(1)∵椭圆的焦点为(0,±3),
∴所求双曲线方程设为:,
又点(-2,)在双曲线上,
∴,解得a2=5或a2=18(舍去).
∴所求双曲线方程为.
(2)∵双曲线的焦点为(±2,0),
∴设所求双曲线方程为:,
又点(3,2)在双曲线上,
∴,解得a2=12或30(舍去),
∴所求双曲线方程为.
【总结升华】根据焦点所在轴的位置合理的设出方程是求双曲线方程的基本步骤。
举一反三:
【变式1】(2018 安徽卷)下列双曲线中,焦点在y轴上且渐近线方程为y=±2x的是( )
(A) (B) (C) (D)
【答案】 C
【解析】
由题意:选项中A,B焦点在x轴,排除
C项的渐近线方程为,即y=±2x,
故选C.
【变式2】(2018 上海)已知点和的横坐标相同,的纵坐标是的纵坐标的2倍,和的轨迹分别为双曲线和,若的渐近线方程为,则的渐近线方程为 .
【答案】;
【解析】设点和的坐标为、,则有
又因为的渐近线方程为,故设的方程为,
把点坐标代入,可得,令,即为曲线的渐近线方程,即。
故答案为。
类型二:直线与双曲线的位置关系
例2.已知双曲线x2-y2=4,直线l:y=k(x-1),讨论直线与双曲线公共点个数.
【解析】联立方程组消去y,并依x聚项整理得:
(1-k2)·x2+2k2x-k2-4=0 ①
(1)当1-k2=0即k=±1时,方程①可化为2x=5,x=,方程组只有一组解,故直线与双曲线只有一个公共点(实质上是直线与渐近线平行时的两种情况,相交但不相切).
(2)当1-k2≠0时,即k≠±1,此时有Δ=4·(4-3k2)若4-3k2>0(k2≠1),
则k∈,方程组有两解,故直线与双曲线有两交点.
(3)若4-3k2=0(k2≠1),则k=±,方程组有解,故直线与双曲线有一个公共点(相切的情况).
(4)若4-3k2<0且k2≠1则k∈,方程组无解,故直线与双曲线无交点.
综上所述,当k=±1或k=±时,直线与双曲线有一个公共点;
当k∈时,直线与双曲线有两个公共点;
当k∈时,直线与双曲线无公共点.
【总结升华】本题通过方程组解的个数来判断直线与双曲线交点的个数,具体操作时,运用了重要的数学方法——分类讨论,而且是“双向讨论”,既要讨论首项系数1——k2是否为0,又要讨论Δ的三种情况,为理清讨论的思路,可画“树枝图”如图:
举一反三:
【变式1】过原点的直线l与双曲线=-1交于两点,则直线l的斜率取值范围是 ( )
A. B.
C. D.
【答案】B
【变式2】直线y=x+3与曲线-x·|x|+y2=1的交点个数是 ( )
A.0 B.1 C.2 D.3?
【答案】D
例3.过点与双曲线有且只有一个公共点的直线有几条,分别求出它们的方程。
【解析】若直线的斜率不存在时,则,此时仅有一个交点,满足条件;
若直线的斜率存在时,设直线的方程为则,
, ∴,
,
当时,方程无解,不满足条件;
当时,方程有一解,满足条件;
当时,令,化简得:无解,所以不满足条件;
所以满足条件的直线有两条和。
【总结升华】直线与双曲线有一个公共点时可能相切也可能相交,注意直线的特殊位置和所过的特殊点.
举一反三:
【变式】双曲线的右焦点到直线x-y-1=0的距离为,且.
(1)求此双曲线的方程;
(2)设直线y=kx+m(m≠0)与双曲线交于不同两点C、D,若点A坐标为(0,-b),且|AC|=|AD|,求实数k取值范围。
【答案】(1)
(2)
类型三:双曲线的弦
例4.(1)求直线被双曲线截得的弦长;
(2)求过定点的直线被双曲线截得的弦中点轨迹方程.
解:由得得(*)
设方程(*)的解为,则有 得,
.
(2)方法一:若该直线的斜率不存在时与双曲线无交点,则设直线的方程为,它被双曲线截得的弦为对应的中点为,
由得(*)
设方程(*)的解为,则 ∴,
且,
∴,
得或.
方法二:设弦的两个端点坐标为,弦中点为,则
得:,
∴, 即,
即(图象的一部分)
【总结升华】(1)弦长公式;
(2)注意上例中有关中点弦问题的两种处理方法.
举一反三:
【变式】垂直于直线的直线被双曲线截得的弦长为,求直线的方程
【答案】
类型四:双曲线的综合问题
例5.设双曲线C:(a>0)与直线l:x+y=1相交于两个不同的点A、B,求双曲线C的离心率的取值范围.
【解析】由C与l相交于两个不同点,故知方程组有两组不同的实根,
消去y并整理得(1-a2)x2+2a2x-2a2=0①.
所以解得0双曲线的离心率e==,因为0所以e>,且e≠.
即离心率e的取值范围为∪(,+∞).
【总结升华】求离心率的范围应以双曲线几何量的限制为准,构建关于a,b,c的不等关系,从前求出离心率的范围.
举一反三:
【变式】已知a、b、c分别为双曲线的实半轴长、虚半轴长、半焦距,且方程ax2+bx+c=0无实根,则双曲线离心率的取值范围是( )
A.1C.1【答案】 D
例6.设P是双曲线x2-=1的右支上的动点,F为双曲线的右焦点,已知A(3,1),则|PA|+|PF|的最小值为________.
【答案】 -2
【解析】设双曲线的另一个焦点为F′,则有F′(-2,0),F(2,0),连结AF′交双曲线的右支于点P1,连结P1F,则|P1F′|-|P1F|=2a=2.
于是(|PA|+|PF|)min=|P1A|+|P1F|
=|P1A|+(|P1F′|-2)=|AF′|-2=-2.
【总结升华】双曲线的定义是解决有关最值问题的重要依据
举一反三:
【变式1】设,为双曲线=1的右焦点,在双曲线上求一点P,使得 取得最小值时,求P点的坐标.
【答案】P点的坐标为
【变式2】一条斜率为1的直线与离心率为的双曲线交于P、Q两点,直线与y轴交于R点,且,求直线和双曲线方程.
【答案】直线方程;
双曲线方程
【巩固练习】
选择题
1.双曲线的渐近线方程是( )
A. B. C. D.
2.椭圆与双曲线有相同的焦点,则m的值是( )
A.±1 B.1 C.-1 D.不存在
3.(2018 新课标Ⅱ文改编)已知双曲线过点,且渐近线方程为,则该双曲线的标准方程为( ).
A. B. C. D.
4.双曲线mx2+y2=1的虚轴长是实轴长的2倍,则m等于( )
A.- B.-4 C.4 D.
5. (2018 唐山二模)在中,AB=2BC,以A,B为焦点,经过C的椭圆和双曲线的离心率分别为,则( )
A. B. C. D.
6.(2018 湖北)将离心率为e1的双曲线C1的实半轴长a和虚半轴长b(a≠b)同时增加m(m>0)个单位长度,得到离心率为e2的双曲线C2,则()
A.对任意的a,b,e1>e2B.当a>b时,e1>e2;当a<b时,e1<e2
C.对任意的a,b,e1<e2 D.当a>b时,e1<e2;当a<b时,e1>e2
二、填空题
7.已知双曲线的右焦点为F,若过点F的直线与双曲线的右支有且只有一个交点,则此直线斜率的取值范围是________.
8.过点P(3,0)的直线l与双曲线4x2-9y2=36只有一个公共点,则这样的直线l共有________条.
9.已知双曲线 (a>0,b>0)的左、右焦点分别是F1,F2,点P在双曲线右支上,且|PF1|=4|PF2|,则此双曲线离心率e的最大值为________.
10.设一个圆的圆心在双曲线的上支上,且恰好经过双曲线的上顶点和上焦点,则原点O到该圆圆心的距离是________.
三、解答题
11.已知双曲线的中心在原点,焦点为F1,F2(0,),且离心率,求双曲线的标准方程及其渐近线.
12.设双曲线C:相交于两个不同的点A、B;求双曲线C的离心率e的取值范围:
13.设双曲线=1(014.两共轭双曲线的离心率分别为,证明:=1.
15. 如图所示,已知F1,F2为双曲线 (a>0,b>0)的两个焦点,过F2作垂直于x轴的直线交双曲线于点P,且∠PF1F2=30°,求双曲线的渐近线方程.
【答案与解析】
1.【答案】:C
【解析】:将双曲线化为,以0代替1,得,即;
即 ,故选C
2.【答案】: A
【解析】: 验证法:当m=±1时,m2=1,
对椭圆来说,a2=4,b2=1,c2=3.
对双曲线来说,a2=1,b2=2,c2=3,
故当m=±1时,它们有相同的焦点.
直接法:显然双曲线焦点在x轴上,故4-m2=m2+2.
∴m2=1,即m=±1.
3.【答案】: A
【解析】:根据双曲线渐近方程为,可设双曲线的方程为,把代入得m=1.所以双曲线的方程为,故选A。
4. 【答案】: A
【解析】: 双曲线mx2+y2=1的方程可化为:
y2-=1,
∴a2=1,b2=-,由2b=4a,
∴2=4,∴m=-.
5. 【答案】: A
【解析】以AB所在直线为x轴,其中点为原点,建立坐标系,则A(-1,0),B(1,0),C(),
所以
对于椭圆而言,2C=2,2a=AC+BC=
所以
对于双曲线而言,2c=2,2a=AC-BC=
所以
故
故选:A。
6. 【答案】:D
【解析】 依题意,,
因为,由于m>0,a>0,b>0,
所以当a>b时,,所以e1<e2;
当a<b时,,而,所以,所以e1>e2.
所以当a>b时,e1<e2;当a<b时,e1>e2.
故选D.
7.【答案】:
【解析】:由题意知F(4,0),双曲线的两条渐近线方程为y=±x,当过点F的直线与渐近线平行时,满足与右支只有一个交点,画出图形,通过图形可知该直线斜率的取值范围是.
8.【答案】:3
【解析】:已知双曲线方程为,故P(3,0)为双曲线的右顶点,所以过P点且与双曲线只有一个公共点的直线共有三条(一条切线和两条与渐近线平行的直线).
9. 【答案】:
【解析】:由|PF1|-|PF2|=2a及|PF1|=4|PF2|得:
|PF2|=,又|PF2≥c-a,
所以≥c-a,c≤,
∴e=≤,即e的最大值为.
10.【答案】:
【解析】:由已知得双曲线的上顶点为A(0,3),上焦点为F(0,5),设圆心为P(x0,y0),则y0==4.代入双曲线方程得,所以,故|PO|==.
11. 解析: 由条件知焦点在y轴上,,;可求;所以双曲线的方程为渐近线方程为
12.解析:由C与t相交于两个不同的点,故知方程组
有两个不同的实数解.消去y并整理得 (1-a2)x2+2a2x-2a2=0.
双曲线的离心率
13.【解析】:由已知,的方程为ay+bx-ab=0,
原点到的距离为,则有,
又c2=a2+b2, ∴,两边平方,得16a2(c2-a2)=3c4.
两边同除以a4并整理得3e4-16e2+16=0,∴e2=4或.
∵ 0∴e2=4,故e=2.
14.解析:证明:双曲线的离心率;
双曲线的离心率.
∴.
15. 【解析】:∵在Rt△F1F2P中,∠PF1F2=30°,
∴|PF1|=2|PF2|.
由双曲线的定义知|PF1|-|PF2|=2a,
∴|PF2|=2a.
∴|F1F2|=|PF2|,即2c=2a,∴c2=3a2.
又∵c2=a2+b2,∴2a2=b2.∴=.
故所求双曲线的渐近线方程为y=±x.
【学习目标】
1.能正熟练使用直接法、待定系数法、定义法求双曲线的方程;
2.能熟练运用几何性质(如范围、对称性、顶点、离心率、渐近线)解决相关问题;
3.能够把直线与双曲线的位置关系的问题转化为方程组解的问题,判断位置关系及解决相关问题.
【知识网络】
【要点梳理】
要点一、双曲线的定义及其标准方程
双曲线的定义
在平面内,到两个定点、的距离之差的绝对值等于常数(大于0且)的动点的轨迹叫作双曲线.这两个定点、叫双曲线的焦点,两焦点的距离叫作双曲线的焦距.
双曲线的标准方程:
焦点在x轴上的双曲线的标准方程
说明:焦点是F1(-c,0)、F2(c,0),其中c2=a2-b2
焦点在y轴上的双曲线的标准方程
说明:焦点是F1(0,-c)、F2(0,c),其中c2=a2-b2
要点诠释:求双曲线的标准方程应从“定形”、“定式”和“定值”三个方面去思考.“定形”是指对称中心在原点,以坐标轴为对称轴的情况下,焦点在哪条坐标轴上;“定式”根据“形”设双曲线方程的具体形式;“定量”是指用定义法或待定系数法确定a,b的值.
要点二、双曲线的几何性质
标准方程
图形
性质
焦点
,
,
焦距
范围
,
,
对称性
关于x轴、y轴和原点对称
顶点
轴
实轴长=,虚轴长=
离心率
渐近线方程
要点三、直线与双曲线的位置关系
直线与双曲线的位置关系
将直线的方程与双曲线的方程联立成方程组,消元转化为关于x或y的一元二次方程,其判别式为Δ.
若即,直线与双曲线渐近线平行,直线与双曲线相交与一点;
若即,
①Δ>0直线和双曲线相交直线和双曲线相交,有两个交点;
②Δ=0直线和双曲线相切直线和双曲线相切,有一个公共点;
③Δ<0直线和双曲线相离直线和双曲线相离,无公共点.
直线与双曲线的相交弦
设直线交双曲线于点两点,则
==
同理可得
这里的求法通常使用韦达定理,需作以下变形:
双曲线的中点弦问题
遇到中点弦问题常用“韦达定理”或“点差法”求解.
在双曲线中,以为中点的弦所在直线的斜率;
涉及弦长的中点问题,常用“点差法”设而不求,将弦所在直线的斜率、弦的中点坐标联系起来相互转化,同时还应充分挖掘题目的隐含条件,寻找量与量间的关系灵活转化,往往就能事半功倍.
解题的主要规律可以概括为“联立方程求交点,韦达定理求弦长,根的分布找范围,曲线定义不能忘”.
要点四、双曲线的实际应用与最值问题
对于双曲线的实际应用问题,我们要抽象出相应的数学问题,即建立数学模型,一般要先建立直角坐标系,然后利用双曲线定义,构建参数a,b,c之间的关系,得到双曲线方程,利用方程求解
双曲线中的最值问题,按照转化途径主要有以下三种:
利用定义转化
利用双曲线的几何性质
转化为函数求最值
【典型例题】
类型一:双曲线的方程与性质
例1.求下列双曲线的标准方程.
(1)与椭圆共焦点,且过点(-2,)的双曲线;
(2)与双曲线有公共焦点,且过点(3,2)的双曲线.
【解析】(1)∵椭圆的焦点为(0,±3),
∴所求双曲线方程设为:,
又点(-2,)在双曲线上,
∴,解得a2=5或a2=18(舍去).
∴所求双曲线方程为.
(2)∵双曲线的焦点为(±2,0),
∴设所求双曲线方程为:,
又点(3,2)在双曲线上,
∴,解得a2=12或30(舍去),
∴所求双曲线方程为.
【总结升华】根据焦点所在轴的位置合理的设出方程是求双曲线方程的基本步骤。
举一反三:
【变式1】(2018 安徽卷)下列双曲线中,焦点在y轴上且渐近线方程为y=±2x的是( )
(A) (B) (C) (D)
【答案】 C
【解析】
由题意:选项中A,B焦点在x轴,排除
C项的渐近线方程为,即y=±2x,
故选C.
【变式2】(2018 上海)已知点和的横坐标相同,的纵坐标是的纵坐标的2倍,和的轨迹分别为双曲线和,若的渐近线方程为,则的渐近线方程为 .
【答案】;
【解析】设点和的坐标为、,则有
又因为的渐近线方程为,故设的方程为,
把点坐标代入,可得,令,即为曲线的渐近线方程,即。
故答案为。
类型二:直线与双曲线的位置关系
例2.已知双曲线x2-y2=4,直线l:y=k(x-1),讨论直线与双曲线公共点个数.
【解析】联立方程组消去y,并依x聚项整理得:
(1-k2)·x2+2k2x-k2-4=0 ①
(1)当1-k2=0即k=±1时,方程①可化为2x=5,x=,方程组只有一组解,故直线与双曲线只有一个公共点(实质上是直线与渐近线平行时的两种情况,相交但不相切).
(2)当1-k2≠0时,即k≠±1,此时有Δ=4·(4-3k2)若4-3k2>0(k2≠1),
则k∈,方程组有两解,故直线与双曲线有两交点.
(3)若4-3k2=0(k2≠1),则k=±,方程组有解,故直线与双曲线有一个公共点(相切的情况).
(4)若4-3k2<0且k2≠1则k∈,方程组无解,故直线与双曲线无交点.
综上所述,当k=±1或k=±时,直线与双曲线有一个公共点;
当k∈时,直线与双曲线有两个公共点;
当k∈时,直线与双曲线无公共点.
【总结升华】本题通过方程组解的个数来判断直线与双曲线交点的个数,具体操作时,运用了重要的数学方法——分类讨论,而且是“双向讨论”,既要讨论首项系数1——k2是否为0,又要讨论Δ的三种情况,为理清讨论的思路,可画“树枝图”如图:
举一反三:
【变式1】过原点的直线l与双曲线=-1交于两点,则直线l的斜率取值范围是 ( )
A. B.
C. D.
【答案】B
【变式2】直线y=x+3与曲线-x·|x|+y2=1的交点个数是 ( )
A.0 B.1 C.2 D.3?
【答案】D
例3.过点与双曲线有且只有一个公共点的直线有几条,分别求出它们的方程。
【解析】若直线的斜率不存在时,则,此时仅有一个交点,满足条件;
若直线的斜率存在时,设直线的方程为则,
, ∴,
,
当时,方程无解,不满足条件;
当时,方程有一解,满足条件;
当时,令,化简得:无解,所以不满足条件;
所以满足条件的直线有两条和。
【总结升华】直线与双曲线有一个公共点时可能相切也可能相交,注意直线的特殊位置和所过的特殊点.
举一反三:
【变式】双曲线的右焦点到直线x-y-1=0的距离为,且.
(1)求此双曲线的方程;
(2)设直线y=kx+m(m≠0)与双曲线交于不同两点C、D,若点A坐标为(0,-b),且|AC|=|AD|,求实数k取值范围。
【答案】(1)
(2)
类型三:双曲线的弦
例4.(1)求直线被双曲线截得的弦长;
(2)求过定点的直线被双曲线截得的弦中点轨迹方程.
解:由得得(*)
设方程(*)的解为,则有 得,
.
(2)方法一:若该直线的斜率不存在时与双曲线无交点,则设直线的方程为,它被双曲线截得的弦为对应的中点为,
由得(*)
设方程(*)的解为,则 ∴,
且,
∴,
得或.
方法二:设弦的两个端点坐标为,弦中点为,则
得:,
∴, 即,
即(图象的一部分)
【总结升华】(1)弦长公式;
(2)注意上例中有关中点弦问题的两种处理方法.
举一反三:
【变式】垂直于直线的直线被双曲线截得的弦长为,求直线的方程
【答案】
类型四:双曲线的综合问题
例5.设双曲线C:(a>0)与直线l:x+y=1相交于两个不同的点A、B,求双曲线C的离心率的取值范围.
【解析】由C与l相交于两个不同点,故知方程组有两组不同的实根,
消去y并整理得(1-a2)x2+2a2x-2a2=0①.
所以解得0
即离心率e的取值范围为∪(,+∞).
【总结升华】求离心率的范围应以双曲线几何量的限制为准,构建关于a,b,c的不等关系,从前求出离心率的范围.
举一反三:
【变式】已知a、b、c分别为双曲线的实半轴长、虚半轴长、半焦距,且方程ax2+bx+c=0无实根,则双曲线离心率的取值范围是( )
A.1
例6.设P是双曲线x2-=1的右支上的动点,F为双曲线的右焦点,已知A(3,1),则|PA|+|PF|的最小值为________.
【答案】 -2
【解析】设双曲线的另一个焦点为F′,则有F′(-2,0),F(2,0),连结AF′交双曲线的右支于点P1,连结P1F,则|P1F′|-|P1F|=2a=2.
于是(|PA|+|PF|)min=|P1A|+|P1F|
=|P1A|+(|P1F′|-2)=|AF′|-2=-2.
【总结升华】双曲线的定义是解决有关最值问题的重要依据
举一反三:
【变式1】设,为双曲线=1的右焦点,在双曲线上求一点P,使得 取得最小值时,求P点的坐标.
【答案】P点的坐标为
【变式2】一条斜率为1的直线与离心率为的双曲线交于P、Q两点,直线与y轴交于R点,且,求直线和双曲线方程.
【答案】直线方程;
双曲线方程
【巩固练习】
选择题
1.双曲线的渐近线方程是( )
A. B. C. D.
2.椭圆与双曲线有相同的焦点,则m的值是( )
A.±1 B.1 C.-1 D.不存在
3.(2018 新课标Ⅱ文改编)已知双曲线过点,且渐近线方程为,则该双曲线的标准方程为( ).
A. B. C. D.
4.双曲线mx2+y2=1的虚轴长是实轴长的2倍,则m等于( )
A.- B.-4 C.4 D.
5. (2018 唐山二模)在中,AB=2BC,以A,B为焦点,经过C的椭圆和双曲线的离心率分别为,则( )
A. B. C. D.
6.(2018 湖北)将离心率为e1的双曲线C1的实半轴长a和虚半轴长b(a≠b)同时增加m(m>0)个单位长度,得到离心率为e2的双曲线C2,则()
A.对任意的a,b,e1>e2B.当a>b时,e1>e2;当a<b时,e1<e2
C.对任意的a,b,e1<e2 D.当a>b时,e1<e2;当a<b时,e1>e2
二、填空题
7.已知双曲线的右焦点为F,若过点F的直线与双曲线的右支有且只有一个交点,则此直线斜率的取值范围是________.
8.过点P(3,0)的直线l与双曲线4x2-9y2=36只有一个公共点,则这样的直线l共有________条.
9.已知双曲线 (a>0,b>0)的左、右焦点分别是F1,F2,点P在双曲线右支上,且|PF1|=4|PF2|,则此双曲线离心率e的最大值为________.
10.设一个圆的圆心在双曲线的上支上,且恰好经过双曲线的上顶点和上焦点,则原点O到该圆圆心的距离是________.
三、解答题
11.已知双曲线的中心在原点,焦点为F1,F2(0,),且离心率,求双曲线的标准方程及其渐近线.
12.设双曲线C:相交于两个不同的点A、B;求双曲线C的离心率e的取值范围:
13.设双曲线=1(0
15. 如图所示,已知F1,F2为双曲线 (a>0,b>0)的两个焦点,过F2作垂直于x轴的直线交双曲线于点P,且∠PF1F2=30°,求双曲线的渐近线方程.
【答案与解析】
1.【答案】:C
【解析】:将双曲线化为,以0代替1,得,即;
即 ,故选C
2.【答案】: A
【解析】: 验证法:当m=±1时,m2=1,
对椭圆来说,a2=4,b2=1,c2=3.
对双曲线来说,a2=1,b2=2,c2=3,
故当m=±1时,它们有相同的焦点.
直接法:显然双曲线焦点在x轴上,故4-m2=m2+2.
∴m2=1,即m=±1.
3.【答案】: A
【解析】:根据双曲线渐近方程为,可设双曲线的方程为,把代入得m=1.所以双曲线的方程为,故选A。
4. 【答案】: A
【解析】: 双曲线mx2+y2=1的方程可化为:
y2-=1,
∴a2=1,b2=-,由2b=4a,
∴2=4,∴m=-.
5. 【答案】: A
【解析】以AB所在直线为x轴,其中点为原点,建立坐标系,则A(-1,0),B(1,0),C(),
所以
对于椭圆而言,2C=2,2a=AC+BC=
所以
对于双曲线而言,2c=2,2a=AC-BC=
所以
故
故选:A。
6. 【答案】:D
【解析】 依题意,,
因为,由于m>0,a>0,b>0,
所以当a>b时,,所以e1<e2;
当a<b时,,而,所以,所以e1>e2.
所以当a>b时,e1<e2;当a<b时,e1>e2.
故选D.
7.【答案】:
【解析】:由题意知F(4,0),双曲线的两条渐近线方程为y=±x,当过点F的直线与渐近线平行时,满足与右支只有一个交点,画出图形,通过图形可知该直线斜率的取值范围是.
8.【答案】:3
【解析】:已知双曲线方程为,故P(3,0)为双曲线的右顶点,所以过P点且与双曲线只有一个公共点的直线共有三条(一条切线和两条与渐近线平行的直线).
9. 【答案】:
【解析】:由|PF1|-|PF2|=2a及|PF1|=4|PF2|得:
|PF2|=,又|PF2≥c-a,
所以≥c-a,c≤,
∴e=≤,即e的最大值为.
10.【答案】:
【解析】:由已知得双曲线的上顶点为A(0,3),上焦点为F(0,5),设圆心为P(x0,y0),则y0==4.代入双曲线方程得,所以,故|PO|==.
11. 解析: 由条件知焦点在y轴上,,;可求;所以双曲线的方程为渐近线方程为
12.解析:由C与t相交于两个不同的点,故知方程组
有两个不同的实数解.消去y并整理得 (1-a2)x2+2a2x-2a2=0.
双曲线的离心率
13.【解析】:由已知,的方程为ay+bx-ab=0,
原点到的距离为,则有,
又c2=a2+b2, ∴,两边平方,得16a2(c2-a2)=3c4.
两边同除以a4并整理得3e4-16e2+16=0,∴e2=4或.
∵ 0
14.解析:证明:双曲线的离心率;
双曲线的离心率.
∴.
15. 【解析】:∵在Rt△F1F2P中,∠PF1F2=30°,
∴|PF1|=2|PF2|.
由双曲线的定义知|PF1|-|PF2|=2a,
∴|PF2|=2a.
∴|F1F2|=|PF2|,即2c=2a,∴c2=3a2.
又∵c2=a2+b2,∴2a2=b2.∴=.
故所求双曲线的渐近线方程为y=±x.
