24.1 测量 教案(表格式)
图片预览
文档简介
课题
24.1 测 量
课时
1课时
上课时间
教学目标
1.知识与技能
使学生了解测量是现实生活中必不可少的,能利用图形的相似测量物体的高度.
2.过程与方法
经历现实生活中测量的过程,并利用其解决一些简单的问题.
3.情感、态度与价值观
通过现实情境,培养学生运用知识解决问题的能力和学习数学的兴趣.
教学
重难点
重点:利用图形的相似测量物体的高度,培养学生运用数学知识解决问题的能力.
难点:画出实际问题的平面示意图.
教学活动设计
二次设计
课堂导入
测量在现实生活中随处可见,筑路、修桥等建设活动都需要测量.当我们走进校园,仰头望着操场旗杆上高高飘扬的五星红旗时,你也许很想知道,操场旗杆有多高?能否运用我们所学的知识把旗杆的高度测量出来呢?
探索新知
合作探究
自学指导
试一试
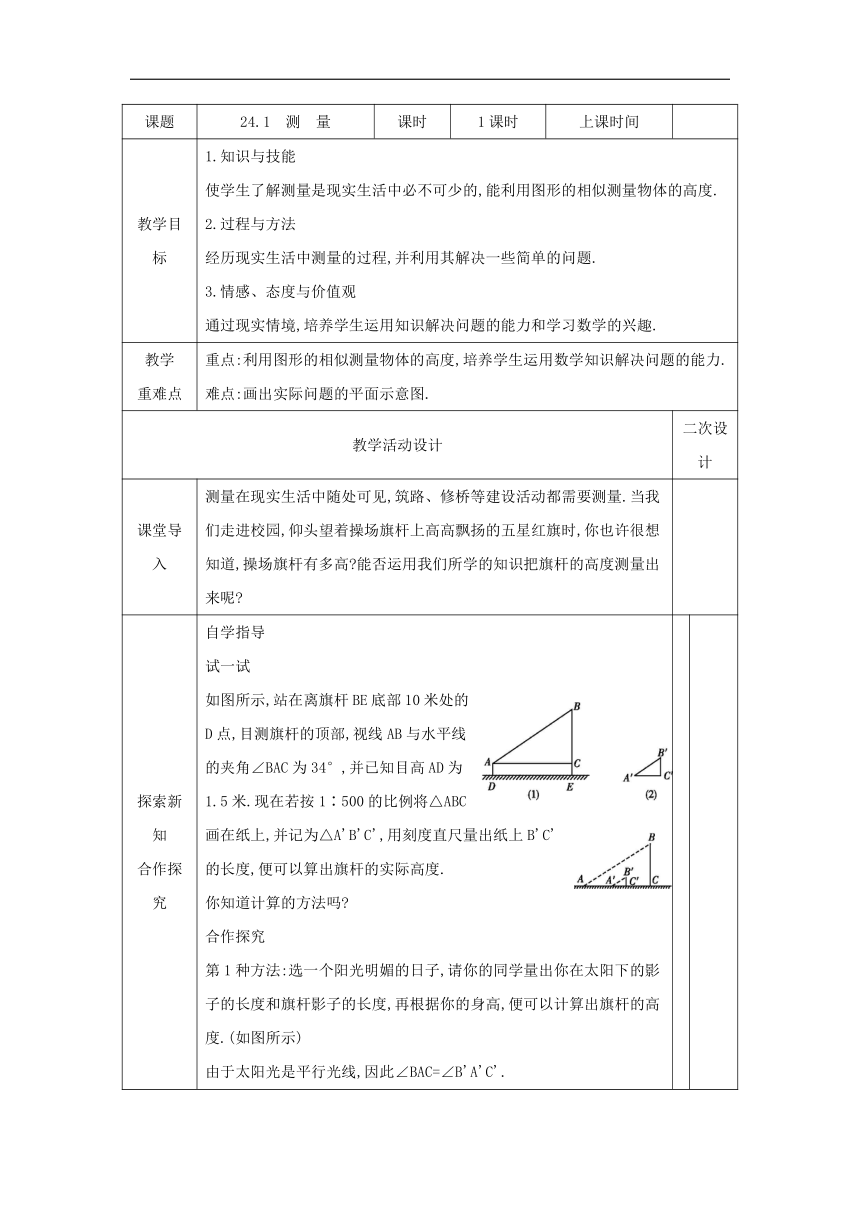
如图所示,站在离旗杆BE底部10米处的D点,目测旗杆的顶部,视线AB与水平线的夹角∠BAC为34°,并已知目高AD为1.5米.现在若按1∶500的比例将△ABC画在纸上,并记为△A'B'C',用刻度直尺量出纸上B'C'的长度,便可以算出旗杆的实际高度.
你知道计算的方法吗?
合作探究
第1种方法:选一个阳光明媚的日子,请你的同学量出你在太阳下的影子的长度和旗杆影子的长度,再根据你的身高,便可以计算出旗杆的高度.(如图所示)
由于太阳光是平行光线,因此∠BAC=∠B'A'C'.
又因为旗杆和人都是垂直于地面的,所以∠BCA=∠B'C'A'=90°.
所以△BAC∽△B'A'C',
BC∶B'C'=AC∶A'C',
BC=.
即可求得旗杆BC的高度.
如果遇到了阴天,就你一个人,是否可以用其他方法测出BC的高度呢?
第2种方法:如图所示,站在离旗杆BE底部10米处的D点,目测旗杆的顶部,视线AB与水平线的夹角∠BAC为34°,并已知目高AD为1.5米.现在请你按1∶500的比例将△ABC画在纸上,并记为△A'B'C',用刻度直尺量出纸上B'C'的长度,便可以算出旗杆的实际高度.
探索新知
合作探究
由画图可知:
因为∠BAC=∠B'A'C'=34°,∠BCA=∠B'C'A'=90°.
所以△BAC∽△B'A'C',B'C'∶BC=1∶500,
所以BC=500B'C',BE=BC+CE,即可算出旗杆的实际高度.
教师指导
1.易错点:
实际测量时,应先设计方案,选择合理方法和测量工具,尽量减少误差.
2.归纳小结:
测量物体高度时一般用到的知识点有哪些?
(1)相似三角形 (2)解直角三角形
3.方法规律:
本节课是用相似三角形的性质来测量旗杆的高度,同学们在学习中应掌握其原理,并学会应用知识解决问题的方法.
当堂训练
1.如图,为测量某建筑物的高度,在离该建筑物底部30.0米处,目测其顶,视线与水平线的夹角为40°,目高为1.5米.试利用相似三角形的知识,求出该建筑物的高度.(精确到0.1米)
2.在平静的湖面上,有一枝红莲,高出水面1米,阵风吹来,红莲被风吹到一边,花朵齐及水面,已知红莲移动的水平距离为2米,问这里水深多少?
3.如图,在一棵树10米高的B处有两只猴子,一只猴子爬下树走到离树20米的池塘A处.另一只猴子爬到树顶D后直接跃到A处.距离以直线计算,如果两只猴子所经过的距离相等,求这棵树的高度.
板书设计
测 量
测量物体高度时一般用到的知识点有哪些?
(1)相似三角形 (2)解直角三角形
教学反思
24.1 测 量
课时
1课时
上课时间
教学目标
1.知识与技能
使学生了解测量是现实生活中必不可少的,能利用图形的相似测量物体的高度.
2.过程与方法
经历现实生活中测量的过程,并利用其解决一些简单的问题.
3.情感、态度与价值观
通过现实情境,培养学生运用知识解决问题的能力和学习数学的兴趣.
教学
重难点
重点:利用图形的相似测量物体的高度,培养学生运用数学知识解决问题的能力.
难点:画出实际问题的平面示意图.
教学活动设计
二次设计
课堂导入
测量在现实生活中随处可见,筑路、修桥等建设活动都需要测量.当我们走进校园,仰头望着操场旗杆上高高飘扬的五星红旗时,你也许很想知道,操场旗杆有多高?能否运用我们所学的知识把旗杆的高度测量出来呢?
探索新知
合作探究
自学指导
试一试
如图所示,站在离旗杆BE底部10米处的D点,目测旗杆的顶部,视线AB与水平线的夹角∠BAC为34°,并已知目高AD为1.5米.现在若按1∶500的比例将△ABC画在纸上,并记为△A'B'C',用刻度直尺量出纸上B'C'的长度,便可以算出旗杆的实际高度.
你知道计算的方法吗?
合作探究
第1种方法:选一个阳光明媚的日子,请你的同学量出你在太阳下的影子的长度和旗杆影子的长度,再根据你的身高,便可以计算出旗杆的高度.(如图所示)
由于太阳光是平行光线,因此∠BAC=∠B'A'C'.
又因为旗杆和人都是垂直于地面的,所以∠BCA=∠B'C'A'=90°.
所以△BAC∽△B'A'C',
BC∶B'C'=AC∶A'C',
BC=.
即可求得旗杆BC的高度.
如果遇到了阴天,就你一个人,是否可以用其他方法测出BC的高度呢?
第2种方法:如图所示,站在离旗杆BE底部10米处的D点,目测旗杆的顶部,视线AB与水平线的夹角∠BAC为34°,并已知目高AD为1.5米.现在请你按1∶500的比例将△ABC画在纸上,并记为△A'B'C',用刻度直尺量出纸上B'C'的长度,便可以算出旗杆的实际高度.
探索新知
合作探究
由画图可知:
因为∠BAC=∠B'A'C'=34°,∠BCA=∠B'C'A'=90°.
所以△BAC∽△B'A'C',B'C'∶BC=1∶500,
所以BC=500B'C',BE=BC+CE,即可算出旗杆的实际高度.
教师指导
1.易错点:
实际测量时,应先设计方案,选择合理方法和测量工具,尽量减少误差.
2.归纳小结:
测量物体高度时一般用到的知识点有哪些?
(1)相似三角形 (2)解直角三角形
3.方法规律:
本节课是用相似三角形的性质来测量旗杆的高度,同学们在学习中应掌握其原理,并学会应用知识解决问题的方法.
当堂训练
1.如图,为测量某建筑物的高度,在离该建筑物底部30.0米处,目测其顶,视线与水平线的夹角为40°,目高为1.5米.试利用相似三角形的知识,求出该建筑物的高度.(精确到0.1米)
2.在平静的湖面上,有一枝红莲,高出水面1米,阵风吹来,红莲被风吹到一边,花朵齐及水面,已知红莲移动的水平距离为2米,问这里水深多少?
3.如图,在一棵树10米高的B处有两只猴子,一只猴子爬下树走到离树20米的池塘A处.另一只猴子爬到树顶D后直接跃到A处.距离以直线计算,如果两只猴子所经过的距离相等,求这棵树的高度.
板书设计
测 量
测量物体高度时一般用到的知识点有哪些?
(1)相似三角形 (2)解直角三角形
教学反思
