23.3.4 相似三角形的应用 课件(30张PPT)
文档属性
| 名称 | 23.3.4 相似三角形的应用 课件(30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 666.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-16 00:00:00 | ||
图片预览





文档简介
课件30张PPT。第23章 图形的相似23.3 相似三角形相似三角形的应用利用影长测量高度
利用相似测量宽度
借助标杆或直尺测量物体的高度1、相似三角形的判断方法有哪些?
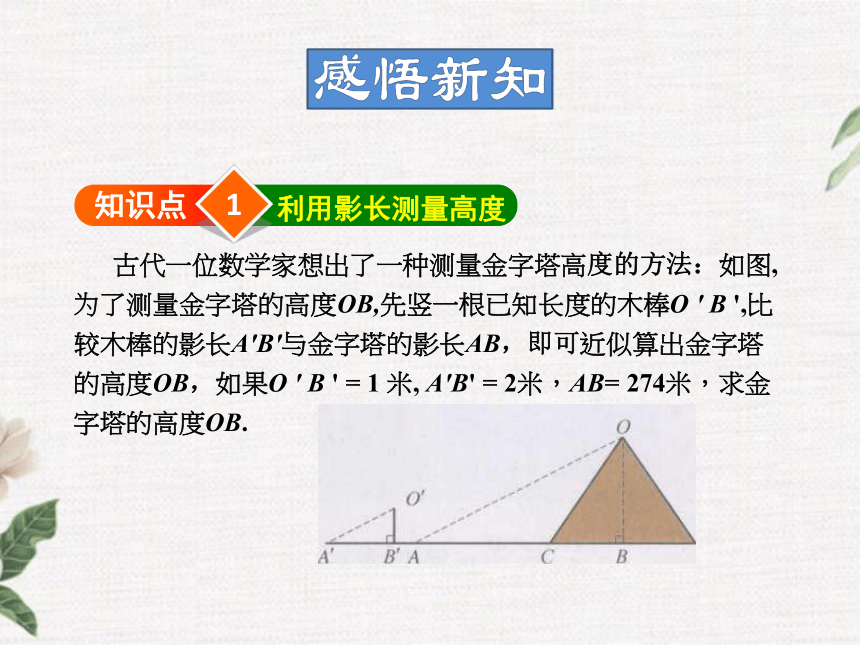
2、相似三角形有哪些性质?复习提问1知识点利用影长测量高度 古代一位数学家想出了一种测量金字塔高度的方法:如图,为了测量金字塔的高度OB,先竖一根已知长度的木棒O ' B ',比较木棒的影长A'B'与金字塔的影长AB,即可近似算出金字塔的高度OB,如果O ' B ' = 1 米, A'B' = 2米,AB= 274米,求金字塔的高度OB. 解:∵太阳光线是平行光线,
∴∠OAB=∠O ' A ' B '.
∵∠ABO= ∠A ' B ' O ' =90°,
∴△OAB∽△ O ' A ' B ' (两角分别
相等的两个三角形相似),
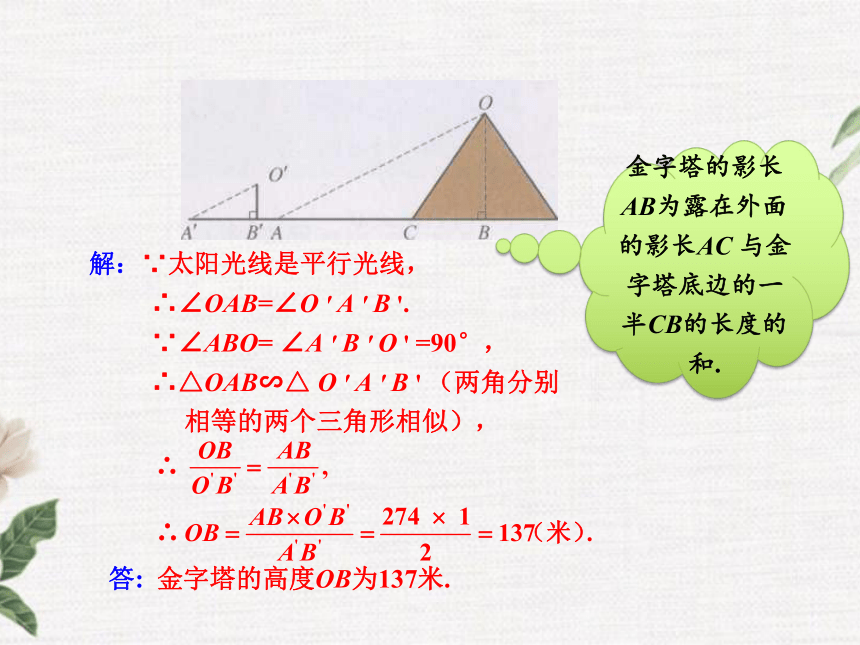
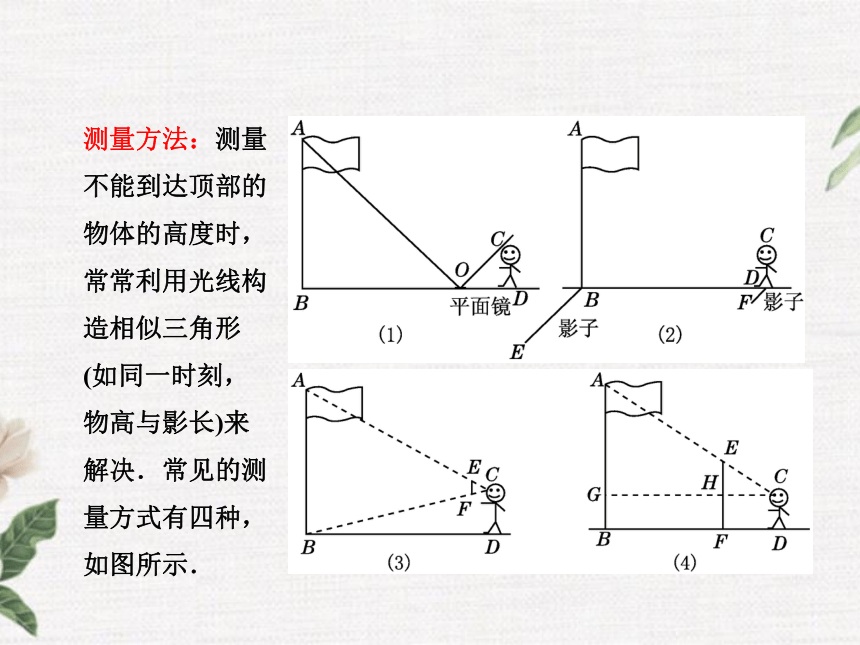
答: 金字塔的高度OB为137米.金字塔的影长AB为露在外面的影长AC 与金字塔底边的一半CB的长度的和.测量方法:测量不能到达顶部的物体的高度时,常常利用光线构造相似三角形(如同一时刻,物高与影长)来解决.常见的测量方式有四种,如图所示.?要点精析:(1) 由于太阳在不停地移动,影子的长也随着太阳的移动而发生变化.因此,度量影子的长一定要在同一时刻下进行,否则就会影响结果的准确性.
(2) 太阳离我们非常远,因此可以把太阳光近似地看成平行光线.
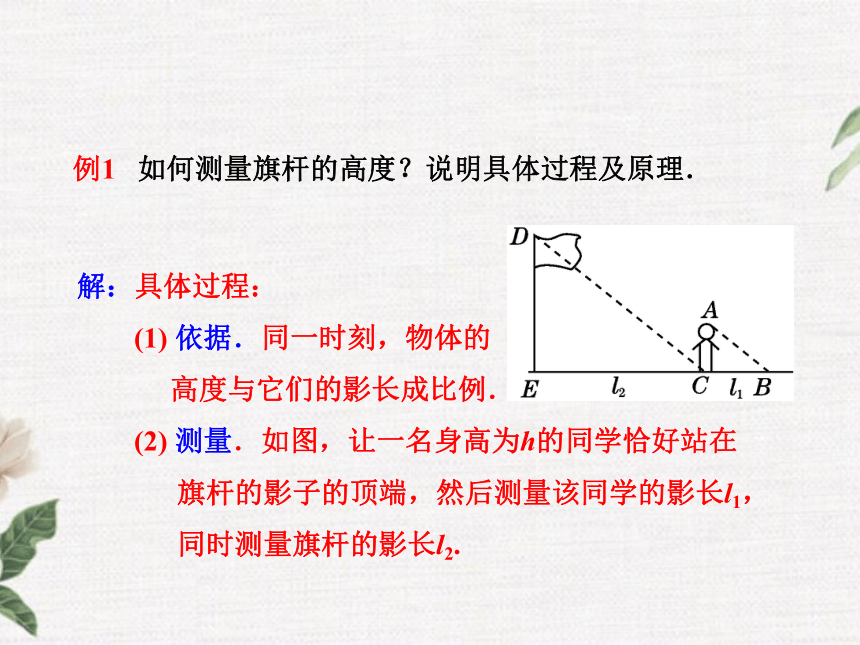
(3) 此方法要求被测物体的底部可以到达,否则测不到被测物体的影长,从而计算不出物体的高.解:具体过程:
(1) 依据.同一时刻,物体的
高度与它们的影长成比例.
(2) 测量.如图,让一名身高为h的同学恰好站在
旗杆的影子的顶端,然后测量该同学的影长l1,
同时测量旗杆的影长l2.例1 如何测量旗杆的高度?说明具体过程及原理. (3) 计算.∵太阳光线是平行光线,
∴AB∥CD,∴∠ABC=∠DCE.
∵∠ACB=∠DEC=90°,
∴△ACB∽△DEC,
∵AC=h, BC=l1, CE=l2,利用影长测量不能直接测量的物高的方法:
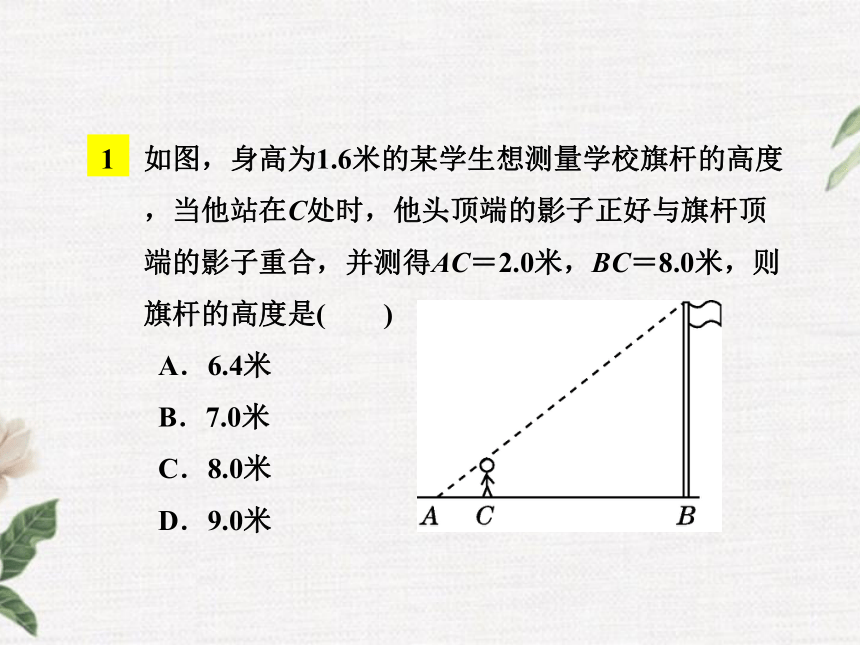
利用同一时刻的太阳光线构造两个相似三角形,利用相似三角形对应边成比例列出关于物高、物影长、人高、人影长的比例式,然后通过测量物影长、人高、人影长来计算出物高.?如图,身高为1.6米的某学生想测量学校旗杆的高度,当他站在C处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AC=2.0米,BC=8.0米,则旗杆的高度是( )
A.6.4米
B.7.0米
C.8.0米
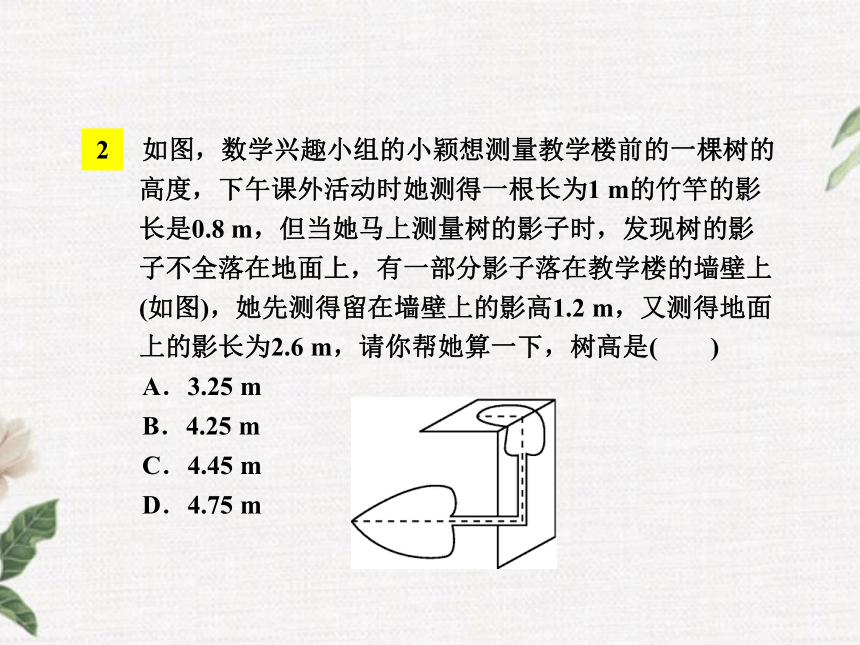
D.9.0米2 如图,数学兴趣小组的小颖想测量教学楼前的一棵树的高度,下午课外活动时她测得一根长为1 m的竹竿的影长是0.8 m,但当她马上测量树的影子时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),她先测得留在墙壁上的影高1.2 m,又测得地面上的影长为2.6 m,请你帮她算一下,树高是( )
A.3.25 m
B.4.25 m
C.4.45 m
D.4.75 m2知识点利用相似测量宽度 如图, 为了估算河的宽度,我们可以在河的对岸选定一个目标作为点A,再在河的这一边选定点B和C,使AB丄BC,然后,再选定点E,
使EC丄BC,用 视线确定BC和
AE的交点D.此时如果测得BD =
118米, DC = 61米,EC = 50米,
求河的宽度AB.(精确到0. 1米)解:∵∠ADB=∠EDC,
∠ABD=∠ECD=90°
∴△ADB∽△ECD(两角分别相等的两个三角
形相似),解得 答:河的宽度AB约为96. 7米.1. 测量方法:测量不能直接到达的两点间的距离时,常常构造相似三角形,利用相似三角形的性质求解.常见的测量方式如下:
① 构造“A”型相似,如图:② 构造“X”型相似,如图.?要点精析:
以前我们曾学过构造全等三角形进行测量的方法.在实际应用中,这种方法虽然能直接通过测量对应边的长得出未知量,但是往往会受到场地、测量仪器等的限制,利用相似三角形的知识,就可以减少限制,所以其应用面更广.2. 利用相似三角形测量的一般步骤:
利用相似三角形的知识对未知量(高度、宽度等)进行测量,一般要经历以下四个步骤:
(1)利用平行线、标杆等构造相似三角形;
(2)测量与表示未知量的线段相对应的边长,以及另
外任意一组对应边的长度;?
(3)画出示意图,利用相似三角形的性质,列出以上
包括未知量在内的四个量的比例式,解出未知量;
(4)检验并得出答案.如图,我们想要测量河两岸相对的两点A,B之间的距离(即河宽).方案:先从B点出发向与AB成90°角的方向走50 m到O处立一标杆,然后方向不变,继续向前走10 m到C处,在C处向右转90°,沿CD方向再走17 m到D处,使得A,
O,D在同一条直线上.那么
A,B之间的距离是多少?例2 解:∵AB⊥BC,CD⊥BC,∴∠ABO=∠DCO=90°.
又 ∵∠AOB=∠DOC,∴△AOB∽△DOC.
∴
∵BO=50 m,CO=10 m,CD=17 m,
∴ ∴AB=85(m).
因此A,B之间的距离是85 m.导引:这是一道测量河宽的实际问题,可以借助相似三角形的对应边成比例得到比例式,所得比例式中有四条线段,测出了三条线段的长,便能求出第四条线段的长. 测量不能直接到达的两点间的距离,关键是构造两个相似三角形,利用能测量的三角形的边长及相似三角形的性质求此距离.如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5 m,EF=0.25 m,目测点D到
地面的距离DG=1.5 m,
到旗杆的水平距离DC=
20 m,求旗杆的高度.3知识点借助标杆或直尺测量物体的高度1. 与测量有关的概念:
(1) 视点:观察物体时人的眼睛称为视点.
(2) 仰角:测量物体的高度时,水平视线与观察物体的视
线间的夹角称为仰角.
(3) 盲区:人的视线看不到的区域称为盲区.
2.测量原理:
用标杆或直尺的高(长)作为三角形的边,利用视点和盲
区的知识构造相似三角形.3.测量方法:如图,观测者的眼睛C必须与标杆的顶端D和物体的顶端A“三点共线”,标杆与地面要垂直,测量出标杆的高度DF,人眼离地面的高度CE,人与标杆的距离EF,标杆与物体的距离FG.利用相似三角形的对应边成比例求物体的高度AG.
要点精析:利用标杆或直尺测量物
体的高度也叫目测,在日常生活
中有着广泛的应用,必要时可以
用自己的身高和臂长等作为测量
工具.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40 cm,EF=20 cm,测得边DF离地面的高度AC=1.5 m,
CD=8 m,则树高
AB=________m.例3 导引:∵∠DEF=∠BCD=90°,∠D=∠D,
∴△DEF∽△DCB,
∵DE=40 cm=0.4 m,EF=20 cm=0.2 m,
CD=8 m,
∴BC=4(m),
∴AB=AC+BC=1.5+4=5.5(m).答案:5.5 解实际问题关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数
学模型来解决问题.如图,利用标杆BE测量建筑物的高度,标杆BE高1.5 m,测得AB=2 m,BC=14 cm,则楼高CD为________.2 如图,我们想要测量河两岸相对的两点A,B之间 的距离(即河宽),你有什么方法?利用相似三角形解决实际问题的方法:
1.利用太阳光线平行构造相似三角形,利用同一时刻物高与
影长成比例构造比例式;画数学图形找相似三角形解决实际问题.
2.没有相似三角形时可以构造直角三角形.
3.对于不易测量的长度或高度,可以转化为易测量的对应线
段,通过对应线段成比例来计算.
利用相似测量宽度
借助标杆或直尺测量物体的高度1、相似三角形的判断方法有哪些?
2、相似三角形有哪些性质?复习提问1知识点利用影长测量高度 古代一位数学家想出了一种测量金字塔高度的方法:如图,为了测量金字塔的高度OB,先竖一根已知长度的木棒O ' B ',比较木棒的影长A'B'与金字塔的影长AB,即可近似算出金字塔的高度OB,如果O ' B ' = 1 米, A'B' = 2米,AB= 274米,求金字塔的高度OB. 解:∵太阳光线是平行光线,
∴∠OAB=∠O ' A ' B '.
∵∠ABO= ∠A ' B ' O ' =90°,
∴△OAB∽△ O ' A ' B ' (两角分别
相等的两个三角形相似),
答: 金字塔的高度OB为137米.金字塔的影长AB为露在外面的影长AC 与金字塔底边的一半CB的长度的和.测量方法:测量不能到达顶部的物体的高度时,常常利用光线构造相似三角形(如同一时刻,物高与影长)来解决.常见的测量方式有四种,如图所示.?要点精析:(1) 由于太阳在不停地移动,影子的长也随着太阳的移动而发生变化.因此,度量影子的长一定要在同一时刻下进行,否则就会影响结果的准确性.
(2) 太阳离我们非常远,因此可以把太阳光近似地看成平行光线.
(3) 此方法要求被测物体的底部可以到达,否则测不到被测物体的影长,从而计算不出物体的高.解:具体过程:
(1) 依据.同一时刻,物体的
高度与它们的影长成比例.
(2) 测量.如图,让一名身高为h的同学恰好站在
旗杆的影子的顶端,然后测量该同学的影长l1,
同时测量旗杆的影长l2.例1 如何测量旗杆的高度?说明具体过程及原理. (3) 计算.∵太阳光线是平行光线,
∴AB∥CD,∴∠ABC=∠DCE.
∵∠ACB=∠DEC=90°,
∴△ACB∽△DEC,
∵AC=h, BC=l1, CE=l2,利用影长测量不能直接测量的物高的方法:
利用同一时刻的太阳光线构造两个相似三角形,利用相似三角形对应边成比例列出关于物高、物影长、人高、人影长的比例式,然后通过测量物影长、人高、人影长来计算出物高.?如图,身高为1.6米的某学生想测量学校旗杆的高度,当他站在C处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AC=2.0米,BC=8.0米,则旗杆的高度是( )
A.6.4米
B.7.0米
C.8.0米
D.9.0米2 如图,数学兴趣小组的小颖想测量教学楼前的一棵树的高度,下午课外活动时她测得一根长为1 m的竹竿的影长是0.8 m,但当她马上测量树的影子时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),她先测得留在墙壁上的影高1.2 m,又测得地面上的影长为2.6 m,请你帮她算一下,树高是( )
A.3.25 m
B.4.25 m
C.4.45 m
D.4.75 m2知识点利用相似测量宽度 如图, 为了估算河的宽度,我们可以在河的对岸选定一个目标作为点A,再在河的这一边选定点B和C,使AB丄BC,然后,再选定点E,
使EC丄BC,用 视线确定BC和
AE的交点D.此时如果测得BD =
118米, DC = 61米,EC = 50米,
求河的宽度AB.(精确到0. 1米)解:∵∠ADB=∠EDC,
∠ABD=∠ECD=90°
∴△ADB∽△ECD(两角分别相等的两个三角
形相似),解得 答:河的宽度AB约为96. 7米.1. 测量方法:测量不能直接到达的两点间的距离时,常常构造相似三角形,利用相似三角形的性质求解.常见的测量方式如下:
① 构造“A”型相似,如图:② 构造“X”型相似,如图.?要点精析:
以前我们曾学过构造全等三角形进行测量的方法.在实际应用中,这种方法虽然能直接通过测量对应边的长得出未知量,但是往往会受到场地、测量仪器等的限制,利用相似三角形的知识,就可以减少限制,所以其应用面更广.2. 利用相似三角形测量的一般步骤:
利用相似三角形的知识对未知量(高度、宽度等)进行测量,一般要经历以下四个步骤:
(1)利用平行线、标杆等构造相似三角形;
(2)测量与表示未知量的线段相对应的边长,以及另
外任意一组对应边的长度;?
(3)画出示意图,利用相似三角形的性质,列出以上
包括未知量在内的四个量的比例式,解出未知量;
(4)检验并得出答案.如图,我们想要测量河两岸相对的两点A,B之间的距离(即河宽).方案:先从B点出发向与AB成90°角的方向走50 m到O处立一标杆,然后方向不变,继续向前走10 m到C处,在C处向右转90°,沿CD方向再走17 m到D处,使得A,
O,D在同一条直线上.那么
A,B之间的距离是多少?例2 解:∵AB⊥BC,CD⊥BC,∴∠ABO=∠DCO=90°.
又 ∵∠AOB=∠DOC,∴△AOB∽△DOC.
∴
∵BO=50 m,CO=10 m,CD=17 m,
∴ ∴AB=85(m).
因此A,B之间的距离是85 m.导引:这是一道测量河宽的实际问题,可以借助相似三角形的对应边成比例得到比例式,所得比例式中有四条线段,测出了三条线段的长,便能求出第四条线段的长. 测量不能直接到达的两点间的距离,关键是构造两个相似三角形,利用能测量的三角形的边长及相似三角形的性质求此距离.如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5 m,EF=0.25 m,目测点D到
地面的距离DG=1.5 m,
到旗杆的水平距离DC=
20 m,求旗杆的高度.3知识点借助标杆或直尺测量物体的高度1. 与测量有关的概念:
(1) 视点:观察物体时人的眼睛称为视点.
(2) 仰角:测量物体的高度时,水平视线与观察物体的视
线间的夹角称为仰角.
(3) 盲区:人的视线看不到的区域称为盲区.
2.测量原理:
用标杆或直尺的高(长)作为三角形的边,利用视点和盲
区的知识构造相似三角形.3.测量方法:如图,观测者的眼睛C必须与标杆的顶端D和物体的顶端A“三点共线”,标杆与地面要垂直,测量出标杆的高度DF,人眼离地面的高度CE,人与标杆的距离EF,标杆与物体的距离FG.利用相似三角形的对应边成比例求物体的高度AG.
要点精析:利用标杆或直尺测量物
体的高度也叫目测,在日常生活
中有着广泛的应用,必要时可以
用自己的身高和臂长等作为测量
工具.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40 cm,EF=20 cm,测得边DF离地面的高度AC=1.5 m,
CD=8 m,则树高
AB=________m.例3 导引:∵∠DEF=∠BCD=90°,∠D=∠D,
∴△DEF∽△DCB,
∵DE=40 cm=0.4 m,EF=20 cm=0.2 m,
CD=8 m,
∴BC=4(m),
∴AB=AC+BC=1.5+4=5.5(m).答案:5.5 解实际问题关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数
学模型来解决问题.如图,利用标杆BE测量建筑物的高度,标杆BE高1.5 m,测得AB=2 m,BC=14 cm,则楼高CD为________.2 如图,我们想要测量河两岸相对的两点A,B之间 的距离(即河宽),你有什么方法?利用相似三角形解决实际问题的方法:
1.利用太阳光线平行构造相似三角形,利用同一时刻物高与
影长成比例构造比例式;画数学图形找相似三角形解决实际问题.
2.没有相似三角形时可以构造直角三角形.
3.对于不易测量的长度或高度,可以转化为易测量的对应线
段,通过对应线段成比例来计算.
