23.4 中位线 课件(23张PPT)
文档属性
| 名称 | 23.4 中位线 课件(23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 455.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-16 16:21:16 | ||
图片预览






文档简介
课件23张PPT。第23章 图形的相似23.4 中位线三角形的中位线
三角形的重心
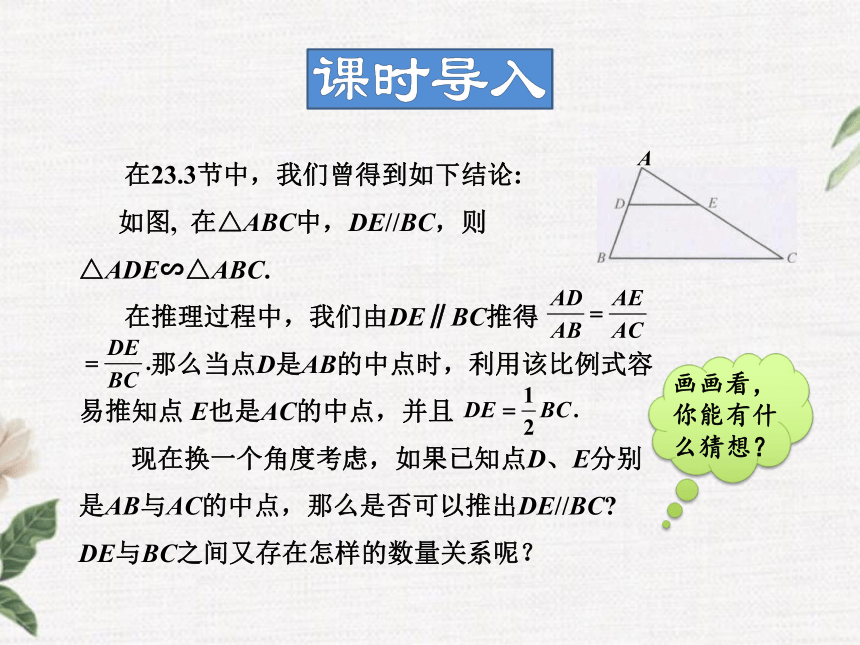
中点四边形 在23.3节中,我们曾得到如下结论:
如图, 在△ABC中,DE//BC,则△ADE∽△ABC.
在推理过程中,我们由DE∥BC推得
那么当点D是AB的中点时,利用该比例式容易推知点 E也是AC的中点,并且
现在换一个角度考虑,如果已知点D、E分别是AB与AC的中点,那么是否可以推出DE//BC?
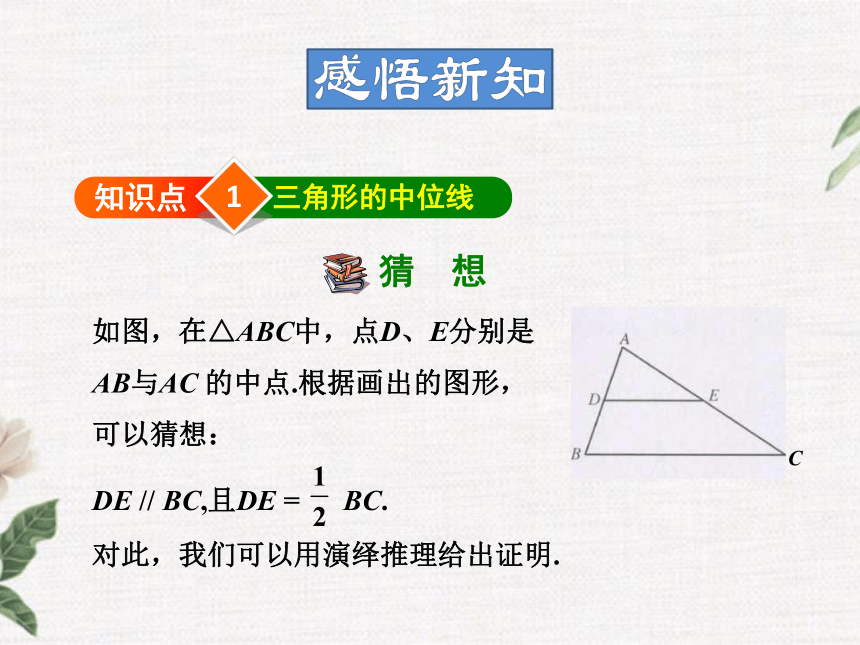
DE与BC之间又存在怎样的数量关系呢?画画看,你能有什么猜想?1知识点三角形的中位线猜 想如图,在△ABC中,点D、E分别是
AB与AC 的中点.根据画出的图形,
可以猜想:
DE // BC,且DE = BC.
对此,我们可以用演绎推理给出证明.在△ABC中,
∵点D、E分别是AB与AC的中点,
∴
∵∠A=∠A,
∴△ADE∽△ABC
∵∠ADE = ∠ABC,
∴证明:1. 三角形中位线的定义: 连结三角形两边中点的线段叫做三角形的中位线.一个三角形共有3条中位线.
易错警示:三角形的中位线要与三角形的中线严格区别开来,三角形的中位线是连结三角形两边中点的线段,而三角形的中线是三角形的顶点与对边中点的连线.
三角形的中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.
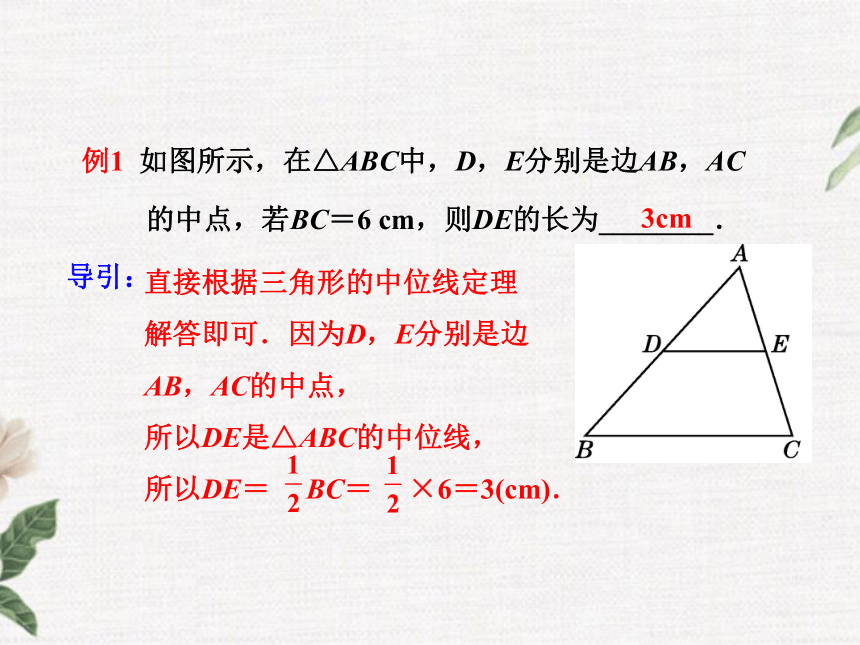
拓展:由三角形三条中位线组成的三角形与原三角形相似,它的周长等于原三角形周长的 ,面积等于原三角形面积的 例1 如图所示,在△ABC中,D,E分别是边AB,AC
的中点,若BC=6 cm,则DE的长为________.直接根据三角形的中位线定理
解答即可.因为D,E分别是边
AB,AC的中点,
所以DE是△ABC的中位线,
所以DE= BC= ×6=3(cm).
3cm导引:证明:连结DE、EF.
∵AD = DB,BE = EC,
∴DE//AC(三角形的中位线平行于第
三边,并且 等于第三边的一半).
同理可得EF//BA.
∴四边形ADEF是平行四边形.
∴ AE、DF互相平分.例2 求证:三角形的一条中位线与第三边上的中线互相
平分. 已知:如图, 在 △ABC 中,AD =DB,
BE=EC, AF = FC. 求证:AE、DF互相平分. 三角形的中位线定理是证明两条线段倍分关系的重要依据.当已知线段的中点求某条线段的长度时,通常要考虑运用三角形的中位线定理解答.如图,以三角形的三个顶点及三边中点为顶点的平行四边形共有( )
A.1个
B.2个
C.3个
D.4个2 如图,在四边形ABCD中,点P是对角线BD的中点,点E,F分别是AB,CD的中点,AD=BC,∠PEF=30°,则∠PFE的度数是( )
A.15°
B.20°
C.25°
D.30°2知识点三角形的重心如图,在△ABC中,D、E分别是边BC、AB的
中点,AD、CE相交于点G.求证:例3证明:连结ED. ∵D、E分别是边BC、AB的中点,
∴DE//AC , (三角形的中位线平行于第
三边,并且等于第三边的一半).
∴△ACG∽△DEG,
∴三角形的重心的定义:三角形的重心是三角形三
条中线的交点.
三角形重心的性质:三角形的重心与一边中点的
连线的长是对应中线长的
例4 如图所示,在△ABC中,G为重心,连结AG并延长,交
边BC于点D,若△ABC的面积为6 cm2,则△BGD的面
积为________.导引: 由点G为△ABC的重心可知AD为
BC边上的中线,且DG= AD,
故S△ABD= S△ABC=3 cm2,
由△BGD与△ABD同高不等底易
得
故S△BGD= S△ABD= ×3=1(cm2).1cm2 已知三角形的重心求线段的长度或比值时,要准确把握以下几点:
三角形的重心与一边中点的连线的长是对应中线
长的
(2) 重心与三角形一个顶点的连线的长是对应中线长
的
(3) 重心分中线所成两条线段的比为2∶1.如图所示,已知点E、F分别是△ABC的边AC、AB的中点,BE、CF相交于点G,FG=1,则CF
的长为( )
A.2 B.1.5 C.3 D.42 给出以下判断:
(1) 线段的中点是线段的重心;
(2) 三角形的三条中线交于一点,这一点就是三角
形的重心;
(3) 平行四边形的重心是它的两条对角线的交点;
(4) 三角形的重心是它的中线的一个三等分点.
那么以上判断中正确的有( )
A.一个 B.两个 C.三个 D.四个3知识点中点四边形1. 中点四边形:顺次连结四边形各边中点所得的四边形叫做中点四边形.
2.常见的中点四边形:
(1) 顺次连结任意四边形各边中点所得的四边形是平行四边形;
(2) 顺次连结矩形各边中点所得的四边形是菱形;
(3) 顺次连结菱形各边中点所得的四边形是矩形;
(4) 顺次连结正方形各边中点所得的四边形是正方形;
(5) 顺次连结等腰梯形各边中点所得的四边形是菱形.如图所示,四边形ABCD中,点E,F,G,H分别是AB,BC,CD,DA的中点.
请判断四边形EFGH的形状,并说明理由;
(2)若四边形EFGH为正方形,则
四边形ABCD的对角线应满足
怎样的条件?(1)由点E,F,G,H分别是各边
的中点可以联想到中位线,故连结AC,把四边形ABCD分成△ABC和△ADC,然后利用三角形的中位线定理判断四边形EFGH的形状;(2)在(1)的基础上结合正方形的判定方法考虑对角线AC,BD应满足的条件.例5 导引:解:(1)四边形EFGH是平行四边形.
理由如下:如图所示,连结AC.
∵E,F分别是AB,BC的中点,
∴EF是△ABC的中位线,
∴EF∥AC,EF= AC.
∵G,H分别是CD,DA的中点,
∴GH是△ADC的中位线, ∴GH∥AC,GH= AC.
∴EF∥GH,EF=GH, ∴四边形EFGH是平行四边形.
(2)四边形ABCD的对角线应满足:AC⊥BD且AC=BD. 本题是一道猜想说理题,首先应根据题目给出的条件进行初步推断,然后进行判断,最后对猜想的结论进行推理论证,以证明猜想的正确性.判断中点四边形的形状,关键是三角形中位线定理的运用. 1 求证:顺次连结四边形各边的中点所得的四边
形是平行边形.运用中位线定理证明线段相等或计算线段长度的方法:
当题目中有中点时,特别是有两个中点时,如果
中点都在一个三角形中,直接用中位线定理.如果不在
一个三角形中,就需要作辅助线取某边上的中点,构
造三 角形的中位线,然后利用中位线定理及相关的知
识解决问题.
三角形的重心
中点四边形 在23.3节中,我们曾得到如下结论:
如图, 在△ABC中,DE//BC,则△ADE∽△ABC.
在推理过程中,我们由DE∥BC推得
那么当点D是AB的中点时,利用该比例式容易推知点 E也是AC的中点,并且
现在换一个角度考虑,如果已知点D、E分别是AB与AC的中点,那么是否可以推出DE//BC?
DE与BC之间又存在怎样的数量关系呢?画画看,你能有什么猜想?1知识点三角形的中位线猜 想如图,在△ABC中,点D、E分别是
AB与AC 的中点.根据画出的图形,
可以猜想:
DE // BC,且DE = BC.
对此,我们可以用演绎推理给出证明.在△ABC中,
∵点D、E分别是AB与AC的中点,
∴
∵∠A=∠A,
∴△ADE∽△ABC
∵∠ADE = ∠ABC,
∴证明:1. 三角形中位线的定义: 连结三角形两边中点的线段叫做三角形的中位线.一个三角形共有3条中位线.
易错警示:三角形的中位线要与三角形的中线严格区别开来,三角形的中位线是连结三角形两边中点的线段,而三角形的中线是三角形的顶点与对边中点的连线.
三角形的中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.
拓展:由三角形三条中位线组成的三角形与原三角形相似,它的周长等于原三角形周长的 ,面积等于原三角形面积的 例1 如图所示,在△ABC中,D,E分别是边AB,AC
的中点,若BC=6 cm,则DE的长为________.直接根据三角形的中位线定理
解答即可.因为D,E分别是边
AB,AC的中点,
所以DE是△ABC的中位线,
所以DE= BC= ×6=3(cm).
3cm导引:证明:连结DE、EF.
∵AD = DB,BE = EC,
∴DE//AC(三角形的中位线平行于第
三边,并且 等于第三边的一半).
同理可得EF//BA.
∴四边形ADEF是平行四边形.
∴ AE、DF互相平分.例2 求证:三角形的一条中位线与第三边上的中线互相
平分. 已知:如图, 在 △ABC 中,AD =DB,
BE=EC, AF = FC. 求证:AE、DF互相平分. 三角形的中位线定理是证明两条线段倍分关系的重要依据.当已知线段的中点求某条线段的长度时,通常要考虑运用三角形的中位线定理解答.如图,以三角形的三个顶点及三边中点为顶点的平行四边形共有( )
A.1个
B.2个
C.3个
D.4个2 如图,在四边形ABCD中,点P是对角线BD的中点,点E,F分别是AB,CD的中点,AD=BC,∠PEF=30°,则∠PFE的度数是( )
A.15°
B.20°
C.25°
D.30°2知识点三角形的重心如图,在△ABC中,D、E分别是边BC、AB的
中点,AD、CE相交于点G.求证:例3证明:连结ED. ∵D、E分别是边BC、AB的中点,
∴DE//AC , (三角形的中位线平行于第
三边,并且等于第三边的一半).
∴△ACG∽△DEG,
∴三角形的重心的定义:三角形的重心是三角形三
条中线的交点.
三角形重心的性质:三角形的重心与一边中点的
连线的长是对应中线长的
例4 如图所示,在△ABC中,G为重心,连结AG并延长,交
边BC于点D,若△ABC的面积为6 cm2,则△BGD的面
积为________.导引: 由点G为△ABC的重心可知AD为
BC边上的中线,且DG= AD,
故S△ABD= S△ABC=3 cm2,
由△BGD与△ABD同高不等底易
得
故S△BGD= S△ABD= ×3=1(cm2).1cm2 已知三角形的重心求线段的长度或比值时,要准确把握以下几点:
三角形的重心与一边中点的连线的长是对应中线
长的
(2) 重心与三角形一个顶点的连线的长是对应中线长
的
(3) 重心分中线所成两条线段的比为2∶1.如图所示,已知点E、F分别是△ABC的边AC、AB的中点,BE、CF相交于点G,FG=1,则CF
的长为( )
A.2 B.1.5 C.3 D.42 给出以下判断:
(1) 线段的中点是线段的重心;
(2) 三角形的三条中线交于一点,这一点就是三角
形的重心;
(3) 平行四边形的重心是它的两条对角线的交点;
(4) 三角形的重心是它的中线的一个三等分点.
那么以上判断中正确的有( )
A.一个 B.两个 C.三个 D.四个3知识点中点四边形1. 中点四边形:顺次连结四边形各边中点所得的四边形叫做中点四边形.
2.常见的中点四边形:
(1) 顺次连结任意四边形各边中点所得的四边形是平行四边形;
(2) 顺次连结矩形各边中点所得的四边形是菱形;
(3) 顺次连结菱形各边中点所得的四边形是矩形;
(4) 顺次连结正方形各边中点所得的四边形是正方形;
(5) 顺次连结等腰梯形各边中点所得的四边形是菱形.如图所示,四边形ABCD中,点E,F,G,H分别是AB,BC,CD,DA的中点.
请判断四边形EFGH的形状,并说明理由;
(2)若四边形EFGH为正方形,则
四边形ABCD的对角线应满足
怎样的条件?(1)由点E,F,G,H分别是各边
的中点可以联想到中位线,故连结AC,把四边形ABCD分成△ABC和△ADC,然后利用三角形的中位线定理判断四边形EFGH的形状;(2)在(1)的基础上结合正方形的判定方法考虑对角线AC,BD应满足的条件.例5 导引:解:(1)四边形EFGH是平行四边形.
理由如下:如图所示,连结AC.
∵E,F分别是AB,BC的中点,
∴EF是△ABC的中位线,
∴EF∥AC,EF= AC.
∵G,H分别是CD,DA的中点,
∴GH是△ADC的中位线, ∴GH∥AC,GH= AC.
∴EF∥GH,EF=GH, ∴四边形EFGH是平行四边形.
(2)四边形ABCD的对角线应满足:AC⊥BD且AC=BD. 本题是一道猜想说理题,首先应根据题目给出的条件进行初步推断,然后进行判断,最后对猜想的结论进行推理论证,以证明猜想的正确性.判断中点四边形的形状,关键是三角形中位线定理的运用. 1 求证:顺次连结四边形各边的中点所得的四边
形是平行边形.运用中位线定理证明线段相等或计算线段长度的方法:
当题目中有中点时,特别是有两个中点时,如果
中点都在一个三角形中,直接用中位线定理.如果不在
一个三角形中,就需要作辅助线取某边上的中点,构
造三 角形的中位线,然后利用中位线定理及相关的知
识解决问题.
