23.1.2 平行线分线段成比例 课件(21张PPT)
文档属性
| 名称 | 23.1.2 平行线分线段成比例 课件(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 422.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-16 00:00:00 | ||
图片预览







文档简介
课件21张PPT。23.1 成比例线段平行线分线段成比例平行线分线段成比例的基本事实
平行线分线段成比例的推论翻开我们的作业本,每一页都是由一些间距相等的平行线组成的.如图23.1.2,在作业本上任意画一条直线m与相邻的三条平行线交于A、B、C三点,得到两条线段AB、BC,那么可以发现所得的这两条线段相等,即AB=BC.如图23.1.3,再任意画一条直线n与这组平行线相交,得到两条线段DE和EF,我们同样可以发现所得的这两条线段相等,即DE=EF.图23.1.2图23.1.3由此,我们可以得到 .试用学过的知识说
明AB=BC,DE=EF1知识点平行线分线段成比例的基本事实做一做选择作业本上不相邻的三条平行线,任意画两条直线m、n与它们相交.如果m、n这两条直线平
行(如图23.1.4),观察并思考这时所
得的AD、DB、FE、EC这四条线段的
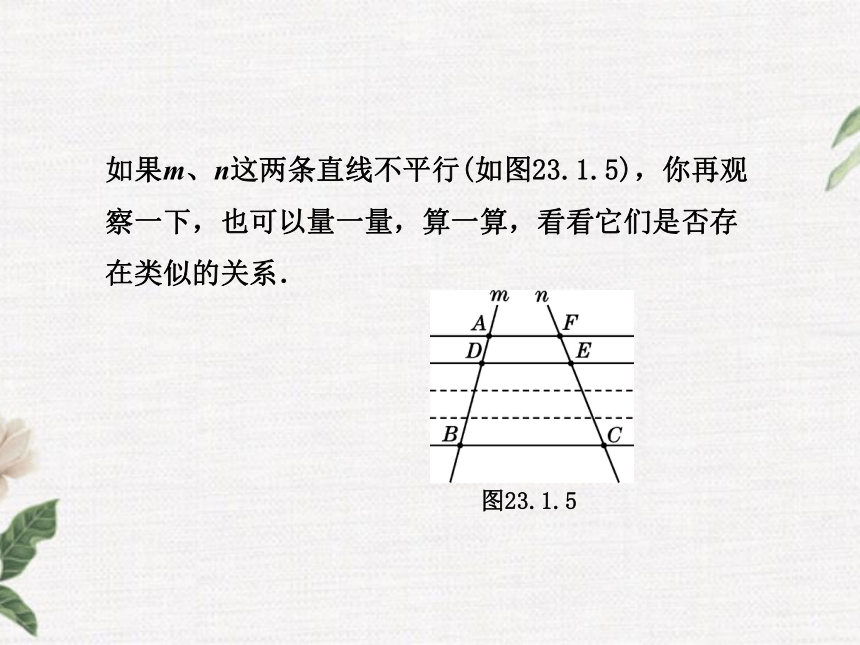
长度有什么关系;图23.1.4如果m、n这两条直线不平行(如图23.1.5),你再观察一下,也可以量一量,算一算,看看它们是否存在类似的关系.图23.1.51.平行线分线段成比例的基本事实:两条直线被一
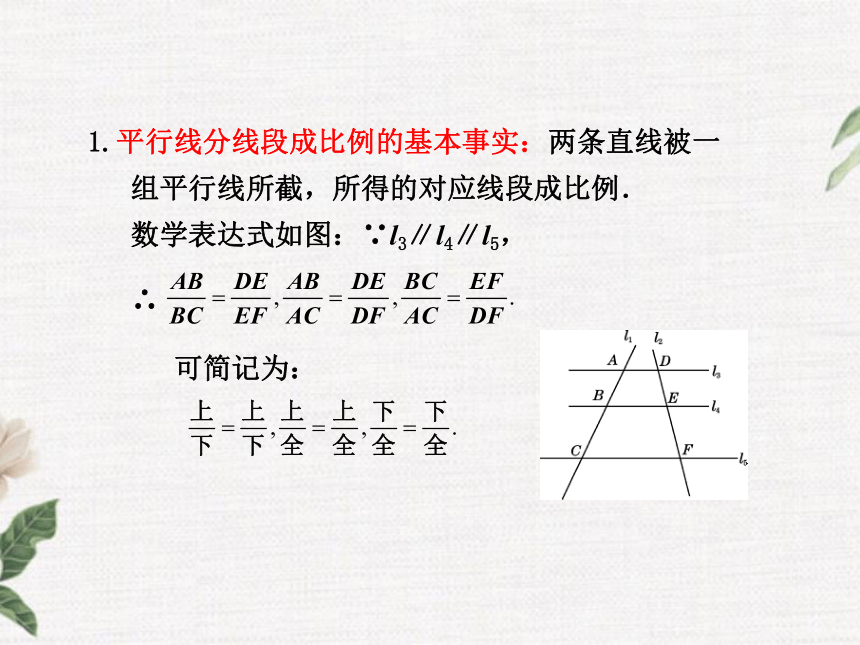
组平行线所截,所得的对应线段成比例.
数学表达式如图:∵l3∥l4∥l5,
∴
可简记为:
要点精析:
(1)一组平行线两两平行,被截直线不一定平行;
(2)所有的成比例线段是指被截直线上的线段,与
这组平行线上的线段无关;
(3)当上比下的值为1时,说明这组平行线间的距
离相等. 例1 如图,l1∥l2∥l3,AB=4,DE=3,EF =6.求
BC的长.解:∵l1∥l2∥l3,
∴ (平行线分线段成比例).
∵AB=4,DE=3,EF=6,
∴
∴BC=8.利用平行线分线段成比例的基本事实求线段长的方法:
先确定图中的平行线,由此联想到线段间的比例关系,结合待求线段和已知线段写出一个含有它们的比例式,构造出方程,解方程求出待求线段长.如图,AD∥BE∥CF,直线l1、l2与这三条平行线
分别交于点A、B、C和点D、E、F,已知AB=1,
BC=3,DE=2,则EF的长为( )
A.4 B.5 C.6 D.8
如图,l1∥l2∥l3,两条直线与这三条平行线分别
交于点A、B、C和D、E、F. 已知 则
的值为( )
A. B. C. D.
2知识点平行线分线段成比例的推论思考1:如图23.1.6,当图23.1.5中的点A与点F重合
时,就形成一个三角形的特殊情形.此时,
AD、DB、AE、EC这四条线段之间会有怎样
的关系呢?图23.1.6如图23.1.6,在△ABC中,DE∥BC,过点A作DE的平行线,那么根据平行线分线段成比例的基本事实,可以得到 再根据比例的有关性质,就有
和 等结论.思考2:如图23.1.7,当图23.1.5中的直线m、n相
交于第二条平行线上某点时,是否也有类
似的成比例线段呢?图23.1.7由此,即有如下结论:
推论:平行于三角形一边的直线截其他两边(或
两边的延长线),所得的对应线段成比例.
数学表达式:如图,∵DE∥BC,
∴要点精析:
(1)本推论实质是平行线分线段成比例的基本事实中一
组平行线中的一条过三角形一顶点,一条在三角
形一边上的一种特殊情况.
(2)成比例线段不涉及平行线所在的边上的线段. 例2 如图,E为?ABCD的边CD延长线上的一点,连结
BE,交AC于点O,交AD于点F.求证: .证明:∵AF ∥ BC,
∴ (平行线分线段成比例).
∵AB∥CE.
∴ (平行线分线段成比例).
∴ .
1 如图,△ABC中,点D、E分别在边 AB、BC上,
DE∥AC.若BD=4,DA=2,BE=3, 则EC=
________.2 如图,在△ABC中,FG∥DE∥BC,已知DF=3,
AG=EC=2,则下列四个等式中一定正确的是
( )
A.FG·DE=6
B.DB·GE=6
C.FG∶DE=2∶3
D.CE∶DB=3∶2平行线除了具备构造“三线八角”得角相等或互补的功能外,还可以分线段成比例,而利用平行线得线段成比例的基本思路是:
1.善于从较复杂的几何图形中分离出基本图形:
“ 型”或“ 型”,得到相应的比例式;
2. 平行是前提条件,没有平行线可以添加辅助线,
一般从分点或中点出发作平行线.
平行线分线段成比例的推论翻开我们的作业本,每一页都是由一些间距相等的平行线组成的.如图23.1.2,在作业本上任意画一条直线m与相邻的三条平行线交于A、B、C三点,得到两条线段AB、BC,那么可以发现所得的这两条线段相等,即AB=BC.如图23.1.3,再任意画一条直线n与这组平行线相交,得到两条线段DE和EF,我们同样可以发现所得的这两条线段相等,即DE=EF.图23.1.2图23.1.3由此,我们可以得到 .试用学过的知识说
明AB=BC,DE=EF1知识点平行线分线段成比例的基本事实做一做选择作业本上不相邻的三条平行线,任意画两条直线m、n与它们相交.如果m、n这两条直线平
行(如图23.1.4),观察并思考这时所
得的AD、DB、FE、EC这四条线段的
长度有什么关系;图23.1.4如果m、n这两条直线不平行(如图23.1.5),你再观察一下,也可以量一量,算一算,看看它们是否存在类似的关系.图23.1.51.平行线分线段成比例的基本事实:两条直线被一
组平行线所截,所得的对应线段成比例.
数学表达式如图:∵l3∥l4∥l5,
∴
可简记为:
要点精析:
(1)一组平行线两两平行,被截直线不一定平行;
(2)所有的成比例线段是指被截直线上的线段,与
这组平行线上的线段无关;
(3)当上比下的值为1时,说明这组平行线间的距
离相等. 例1 如图,l1∥l2∥l3,AB=4,DE=3,EF =6.求
BC的长.解:∵l1∥l2∥l3,
∴ (平行线分线段成比例).
∵AB=4,DE=3,EF=6,
∴
∴BC=8.利用平行线分线段成比例的基本事实求线段长的方法:
先确定图中的平行线,由此联想到线段间的比例关系,结合待求线段和已知线段写出一个含有它们的比例式,构造出方程,解方程求出待求线段长.如图,AD∥BE∥CF,直线l1、l2与这三条平行线
分别交于点A、B、C和点D、E、F,已知AB=1,
BC=3,DE=2,则EF的长为( )
A.4 B.5 C.6 D.8
如图,l1∥l2∥l3,两条直线与这三条平行线分别
交于点A、B、C和D、E、F. 已知 则
的值为( )
A. B. C. D.
2知识点平行线分线段成比例的推论思考1:如图23.1.6,当图23.1.5中的点A与点F重合
时,就形成一个三角形的特殊情形.此时,
AD、DB、AE、EC这四条线段之间会有怎样
的关系呢?图23.1.6如图23.1.6,在△ABC中,DE∥BC,过点A作DE的平行线,那么根据平行线分线段成比例的基本事实,可以得到 再根据比例的有关性质,就有
和 等结论.思考2:如图23.1.7,当图23.1.5中的直线m、n相
交于第二条平行线上某点时,是否也有类
似的成比例线段呢?图23.1.7由此,即有如下结论:
推论:平行于三角形一边的直线截其他两边(或
两边的延长线),所得的对应线段成比例.
数学表达式:如图,∵DE∥BC,
∴要点精析:
(1)本推论实质是平行线分线段成比例的基本事实中一
组平行线中的一条过三角形一顶点,一条在三角
形一边上的一种特殊情况.
(2)成比例线段不涉及平行线所在的边上的线段. 例2 如图,E为?ABCD的边CD延长线上的一点,连结
BE,交AC于点O,交AD于点F.求证: .证明:∵AF ∥ BC,
∴ (平行线分线段成比例).
∵AB∥CE.
∴ (平行线分线段成比例).
∴ .
1 如图,△ABC中,点D、E分别在边 AB、BC上,
DE∥AC.若BD=4,DA=2,BE=3, 则EC=
________.2 如图,在△ABC中,FG∥DE∥BC,已知DF=3,
AG=EC=2,则下列四个等式中一定正确的是
( )
A.FG·DE=6
B.DB·GE=6
C.FG∶DE=2∶3
D.CE∶DB=3∶2平行线除了具备构造“三线八角”得角相等或互补的功能外,还可以分线段成比例,而利用平行线得线段成比例的基本思路是:
1.善于从较复杂的几何图形中分离出基本图形:
“ 型”或“ 型”,得到相应的比例式;
2. 平行是前提条件,没有平行线可以添加辅助线,
一般从分点或中点出发作平行线.
