23.2 相似图形 课件(22张PPT)
文档属性
| 名称 | 23.2 相似图形 课件(22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 433.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-16 00:00:00 | ||
图片预览








文档简介
课件22张PPT。第23章 图形的相似23.2 相似图形相似图形的定义
相似多边形的性质 日常生活中,我们会碰到很多形状相同、大小不一定相同的图形,例如下面两张照片,右边的照片是由左边的照片放大得来的.尽管它们大小不同,但形状相同.我们把这种具有相同形状的图形称为相似图形(similar figures).1知识点相似图形的定义1. 定义:两个形状相同的平面图形叫做相似图形.
要点精析:(1)“形状相同”是判断相似图形的唯一条件;
(2)相似图形之间的关系:两个图形相似,其中一个图形可
以看作由另一个图形放大或缩小得到.
2.易错警示:(1)两个图形相似是指它们的形状相同,与它
们的位置无关.(2)全等图形是一种特殊的相似图形,不
仅形状相同,大小也相同.例1 图中的相似图形有哪些?本题依据相似图形的定义求解.观察这些图形,虽
然图(6)与图(12)、图(8)与图(11)极为相似,但是它
们的形状不相同.图(6)“拉长”而不是整体放大变成
了图(12),图(8)“压缩”而不是整体缩小变成了图(11),
所以它们不是相似图形.而图(1)与图(9)、图(2)与图
(4)、图(3)与图(10)、图(5)与图(7)的形状完全相同,
所以它们是相似图形.导引: 解:相似图形有:图(1)和图(9),图(2)和图(4),图(3)
和图(10),图(5)和图(7).(1)两个图形相似是指它们的形状相同,与它们的位
置无关;
(2)全等图形是一种特殊的相似图形,不仅形状相同,
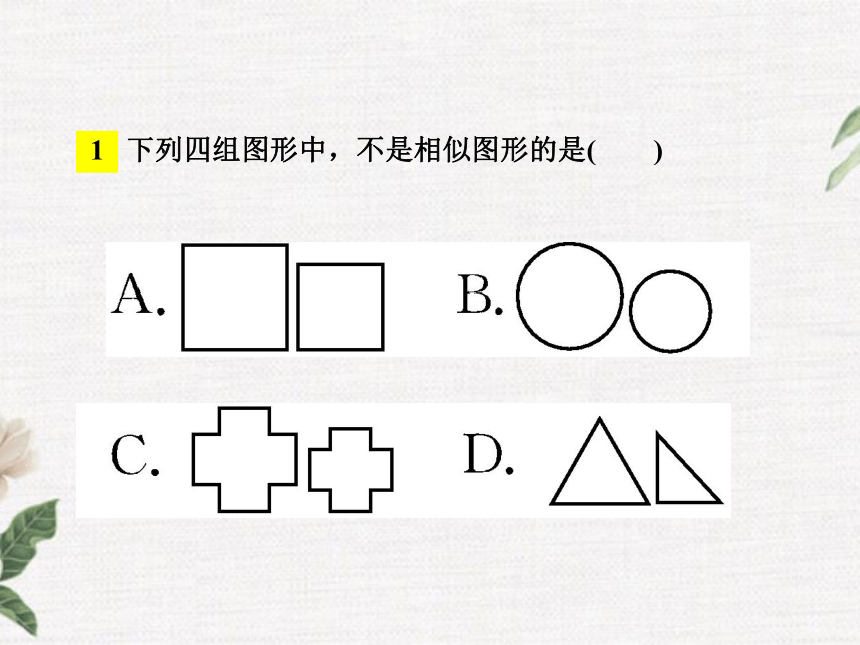
大小也相同.1 下列四组图形中,不是相似图形的是( ) 2 下列说法:
①放大(缩小)的图片与原图片是相似图形;
②比例尺不同的中国地图是相似图形;
③放大镜下的五角星与原来的五角星是相似图形;
④放电影时胶片上的图像和它映射到屏幕上的图
象是相似图形;
⑤平面镜中,你的像与你本人是相似图形.
其中正确的说法有( )
A.2个 B.3个 C.4个 D.5个2知识点相似多边形的性质图23.2.1是大小不同的两张地图,当然,它们是相似的图形.设在大地图中有A、B、C三地,在小地图中相应的三地记为A′、B′、C′,试用刻度尺量一量两张地图中A(A′)与B(B′)两地之间的图上距离和B(B′)与C(C′)两地之间的图上距离,用量角器量一量∠ABC和∠A′B′C′的大小.问 题(一)AB=________cm,BC=________cm;
A′B′=______cm,B′C′=______cm;
∠ABC=______°,∠A′B′C′=______°.我们可以得到∠ABC=∠A′B′C′.但是,两张地图中AB和A′B′、BC和B′C′的长度都是不相等的,那么它们之间有什么关系呢?小地图是由大地图缩小得来的,我们能感到线段A′B′、B′C′的长度与线段AB、BC的长度相比,都“同样程度”地缩小了.计算可得 ________, ________.再算算
你发现了什么?如果在这两张地图中
那么会出现什么情况? 我们能发现 即AB、A′B′、BC、B′C′这四条线段是成比例线段.
实际上,上面两张相似的图形中的对应线段都是成比例的,对应角都是相等的.
这样的结论对一般的相似多边形是否成立呢?1.定义:两个边数相同的多边形,如果各边对应
成比例,各角对应相等,就称这两个多边形相
似.
要点精析:
判定相似多边形的条件:
(1)各角对应相等;
(2)各边对应成比例.2.相似多边形的性质:相似多边形的对应边成比例,
对应角相等.
作用:常用来求相似多边形中未知的边的长度和
角的度数.例2 在图所示的两个相似四边形中,求边 x的长
度和角α的大小.
分析:利用相似多边形的性质和多边形的内角和公
式就可以得到所需结果,在利用相似多边形
的性质时,必须分清对应边和对应角.∵两个四边形相似,
∴ ,
∴x=27.
根据对应角相等,可得
α=360°-(77°+83°+116°)
=84°.解: 利用相似多边形的性质求边长或角度,关键扣住“对应”二字,找准对应边和对应角是解决问题
的关键.需要注意的是对应边是比相等,而对应角
是直接相等.思考 两个三角形一定是相似图形吗?两个等腰三角形呢?两个等边三角形呢?
1 放大镜中的多边形与原多边形的关系是( )
A.形状不同,大小不同
B.形状相同,大小相同
C.形状相同,大小不同
D.形状不同,大小相同
2 若一个三角形三边之比为3∶5∶7,与它相似的三
角形的最长边的长为21,则最短边的长为( )
A.15 B.10
C.9 D.31.相似多边形的定义可作为判断两个多边形是否相
似的判定,即在多边形中,只有“边数相同”
“角分别相等”“边成比例”这三个条件同时成立
时,才能说明这两个多边形是相似多边形.
2.相似比的值与两个多边形的前后顺序有关.
3.相似比为1的两个相似多边形是全等多边形.
相似多边形的性质 日常生活中,我们会碰到很多形状相同、大小不一定相同的图形,例如下面两张照片,右边的照片是由左边的照片放大得来的.尽管它们大小不同,但形状相同.我们把这种具有相同形状的图形称为相似图形(similar figures).1知识点相似图形的定义1. 定义:两个形状相同的平面图形叫做相似图形.
要点精析:(1)“形状相同”是判断相似图形的唯一条件;
(2)相似图形之间的关系:两个图形相似,其中一个图形可
以看作由另一个图形放大或缩小得到.
2.易错警示:(1)两个图形相似是指它们的形状相同,与它
们的位置无关.(2)全等图形是一种特殊的相似图形,不
仅形状相同,大小也相同.例1 图中的相似图形有哪些?本题依据相似图形的定义求解.观察这些图形,虽
然图(6)与图(12)、图(8)与图(11)极为相似,但是它
们的形状不相同.图(6)“拉长”而不是整体放大变成
了图(12),图(8)“压缩”而不是整体缩小变成了图(11),
所以它们不是相似图形.而图(1)与图(9)、图(2)与图
(4)、图(3)与图(10)、图(5)与图(7)的形状完全相同,
所以它们是相似图形.导引: 解:相似图形有:图(1)和图(9),图(2)和图(4),图(3)
和图(10),图(5)和图(7).(1)两个图形相似是指它们的形状相同,与它们的位
置无关;
(2)全等图形是一种特殊的相似图形,不仅形状相同,
大小也相同.1 下列四组图形中,不是相似图形的是( ) 2 下列说法:
①放大(缩小)的图片与原图片是相似图形;
②比例尺不同的中国地图是相似图形;
③放大镜下的五角星与原来的五角星是相似图形;
④放电影时胶片上的图像和它映射到屏幕上的图
象是相似图形;
⑤平面镜中,你的像与你本人是相似图形.
其中正确的说法有( )
A.2个 B.3个 C.4个 D.5个2知识点相似多边形的性质图23.2.1是大小不同的两张地图,当然,它们是相似的图形.设在大地图中有A、B、C三地,在小地图中相应的三地记为A′、B′、C′,试用刻度尺量一量两张地图中A(A′)与B(B′)两地之间的图上距离和B(B′)与C(C′)两地之间的图上距离,用量角器量一量∠ABC和∠A′B′C′的大小.问 题(一)AB=________cm,BC=________cm;
A′B′=______cm,B′C′=______cm;
∠ABC=______°,∠A′B′C′=______°.我们可以得到∠ABC=∠A′B′C′.但是,两张地图中AB和A′B′、BC和B′C′的长度都是不相等的,那么它们之间有什么关系呢?小地图是由大地图缩小得来的,我们能感到线段A′B′、B′C′的长度与线段AB、BC的长度相比,都“同样程度”地缩小了.计算可得 ________, ________.再算算
你发现了什么?如果在这两张地图中
那么会出现什么情况? 我们能发现 即AB、A′B′、BC、B′C′这四条线段是成比例线段.
实际上,上面两张相似的图形中的对应线段都是成比例的,对应角都是相等的.
这样的结论对一般的相似多边形是否成立呢?1.定义:两个边数相同的多边形,如果各边对应
成比例,各角对应相等,就称这两个多边形相
似.
要点精析:
判定相似多边形的条件:
(1)各角对应相等;
(2)各边对应成比例.2.相似多边形的性质:相似多边形的对应边成比例,
对应角相等.
作用:常用来求相似多边形中未知的边的长度和
角的度数.例2 在图所示的两个相似四边形中,求边 x的长
度和角α的大小.
分析:利用相似多边形的性质和多边形的内角和公
式就可以得到所需结果,在利用相似多边形
的性质时,必须分清对应边和对应角.∵两个四边形相似,
∴ ,
∴x=27.
根据对应角相等,可得
α=360°-(77°+83°+116°)
=84°.解: 利用相似多边形的性质求边长或角度,关键扣住“对应”二字,找准对应边和对应角是解决问题
的关键.需要注意的是对应边是比相等,而对应角
是直接相等.思考 两个三角形一定是相似图形吗?两个等腰三角形呢?两个等边三角形呢?
1 放大镜中的多边形与原多边形的关系是( )
A.形状不同,大小不同
B.形状相同,大小相同
C.形状相同,大小不同
D.形状不同,大小相同
2 若一个三角形三边之比为3∶5∶7,与它相似的三
角形的最长边的长为21,则最短边的长为( )
A.15 B.10
C.9 D.31.相似多边形的定义可作为判断两个多边形是否相
似的判定,即在多边形中,只有“边数相同”
“角分别相等”“边成比例”这三个条件同时成立
时,才能说明这两个多边形是相似多边形.
2.相似比的值与两个多边形的前后顺序有关.
3.相似比为1的两个相似多边形是全等多边形.
