23.3.1 相似三角形 课件(23张PPT)
文档属性
| 名称 | 23.3.1 相似三角形 课件(23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 481.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-16 00:00:00 | ||
图片预览








文档简介
课件23张PPT。23.3 相似三角形相似三角形相似三角形及相关概念
平行线判定两三角形相似1、平行线分线段成比例定理及其推论是什么?
2、什么是相似图形?相似多边形?复习提问1知识点相似三角形及相关概念 定义:如果两个三角形中,各角对应相等,各边对应成比例,那么这两个三角形相似.
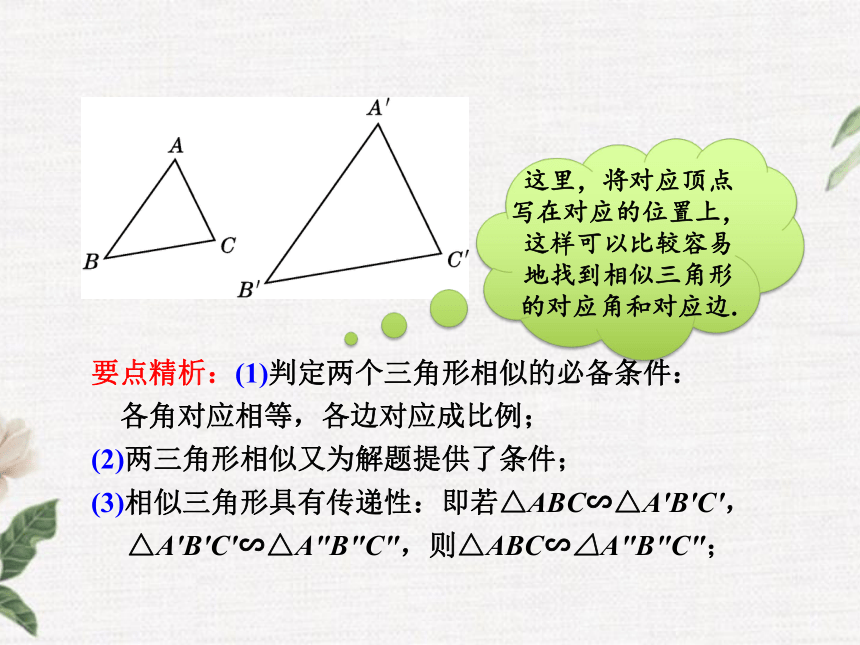
数学表达式:如图下图,在△ABC和△A′B′C′中,△ABC∽△A′B′C′要点精析:(1)判定两个三角形相似的必备条件:
各角对应相等,各边对应成比例;
(2)两三角形相似又为解题提供了条件;
(3)相似三角形具有传递性:即若△ABC∽△A′B′C′,
△A′B′C′∽△A″B″C″,则△ABC∽△A″B″C″;这里,将对应顶点写在对应的位置上,这样可以比较容易地找到相似三角形的对应角和对应边.相似比的定义:相似三角形对应边的比称为相似比.
要点精析:(1)相似比的值与两个三角形的前后顺序有关.
(2) 相似比为1的两个相似三角形为全等三角形.反过来
两个全等三角形可以看作是相似比是1的相似三角形.全等三角形是相似三角形的特例例1 如图,已知△OAC∽△OBD,且OA=4,AC=2,
OB=2,∠C=∠D.
求:(1) △OAC与△OBD的相似比;
(2) BD的长.导引: (1)由△OAC∽△OBD及∠C=
∠D,可找出两个三角形的对应边,即可求出相似比;(2)根据相似三角形对应边成比例,可以列出比例式求出BD的长.解: (1) ∵△OAC∽△OBD,∠C=∠D,
∴线段OA与线段OB是对应边,
∴△OAC与△OBD的相似比为
(2)∵△OAC∽△OBD,
相似三角形的定义具有两重性,即:若两个三角形的各角对应相等且各边对应成比例,则这两个三角形相似;反之,若两个三角形相似,则它们的对应角相等且对应边成比例.因此相似三角形的定义既是相似三角形的性质,也是相似三角形的判定方法.警示:求相似比时,不要忽视相似比的顺序性.下列说法中错误的是( )
A.两个全等三角形一定相似
B.两个直角三角形一定相似
C.两个相似三角形的对应角相等,对应边成比例
D.相似的两个三角形不一定全等如图,△ABC∽△DEF,相似比为 1∶2. 若
BC=1,则EF的长是( )
A.1 B.2 C.3 D.42知识点平行线判定两三角形相似 如图,在△ABC中,D为边AB上的任一点,作DE∥BC,交边AC于点E,用刻度尺和量角器量一量,看看△ADE与△ABC的边角之间有什么关系,进而判断这两个三角形是否相似.做一做 显然,∠ADE=∠ABC,∠AED=
∠ACB,∠A=∠A.
又由平行线分线段成比例的基本事
实,可推得 通过度量,还可
以发现 因而有△ADE∽△ABC.
我们可以用演绎推理证明这一结论. 过点D作AC的平行线交BC于点F,
∴ (平行线分线段成比例),
∴
∴
已知:如图,DE∥BC,并分别交AB、AC于点D、E.
求证:△ADE∽△ABC.证明:∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
(平行线分线段成比例),∴△ADE∽△ABC(相似三角形的定义).∵DE∥BC,DF∥AC,
∴四边形DFCE是平行四边形,
∴DE=FC.
∴
又∵∠ADE=∠B,∠AED=∠C,∠A=∠A,用平行线判定三角形相似的定理:平行于三角形一边的直线,和其他两边(或两边的延长线)相交所构成的三角形与原三角形相似.
数学表达式:如图,∵DE∥BC ∴△ABC∽△ADE.要点精析:(1) 定理中“和其他两边相交”是指和其他两边所在直线相交.
(2) 根据定理得到的相似三角形的三个基本图形中都有
BC∥DE,图(1)(2)很像大写字母A,故我们称之为“A”型相似;图(3)很像大写字母X,故我们称之为“X”型相似(也像阿拉伯数字“8”).2、作用:本定理是相似三角形判定定理的预备定理:它通过平行证三角形相似,再由相似证对应角相等、对应边成比例.例2 如图,在△ABC中,点D是边AB的三等分点,
DE∥BC,DE=5.求BC的长.
解:∵DE∥BC,
∴△ADE∽△ABC(平行于三角形
一边的直线,和其他两边相交所
构成的三角形和原三角形相似),
∴
∴BC=3DE=15.利用证三角形相似求线段的长的方法:当三角形被平行线所截形成“A”型或“X”型的图形,并且所求的线段或已知线段在平行的边上,通常考虑通过证三角形相似,再利用相似三角形的对应边成比例构建包含已知与未知线段的比例式,即可求出线段的长.如图,点P是平行四边形ABCD的边AB上一点,
射线CP交DA的延长线于点E,则图中相似的三
角形有( )
A.0对
B.1对
C.2对
D.3对在△ABC中,DE∥BC,AE∶EC=2∶3,DE
=4,则BC等于( )
A.10 B.8 C.9 D.6 利用平行线证比例式或等积式的方法:当比例式或等积式中的线段不在平行线上时,可直接利用平行线分线段成比例定理证明;当比例式或等积式中的线段有的在平行线上时,可直接利用平行线截三角形相似的对应边成比例证明;当比例式或等积式中的线段不是对应线段时,利用转化思想,用等线段、等比例、等积替换进行论证.
平行线判定两三角形相似1、平行线分线段成比例定理及其推论是什么?
2、什么是相似图形?相似多边形?复习提问1知识点相似三角形及相关概念 定义:如果两个三角形中,各角对应相等,各边对应成比例,那么这两个三角形相似.
数学表达式:如图下图,在△ABC和△A′B′C′中,△ABC∽△A′B′C′要点精析:(1)判定两个三角形相似的必备条件:
各角对应相等,各边对应成比例;
(2)两三角形相似又为解题提供了条件;
(3)相似三角形具有传递性:即若△ABC∽△A′B′C′,
△A′B′C′∽△A″B″C″,则△ABC∽△A″B″C″;这里,将对应顶点写在对应的位置上,这样可以比较容易地找到相似三角形的对应角和对应边.相似比的定义:相似三角形对应边的比称为相似比.
要点精析:(1)相似比的值与两个三角形的前后顺序有关.
(2) 相似比为1的两个相似三角形为全等三角形.反过来
两个全等三角形可以看作是相似比是1的相似三角形.全等三角形是相似三角形的特例例1 如图,已知△OAC∽△OBD,且OA=4,AC=2,
OB=2,∠C=∠D.
求:(1) △OAC与△OBD的相似比;
(2) BD的长.导引: (1)由△OAC∽△OBD及∠C=
∠D,可找出两个三角形的对应边,即可求出相似比;(2)根据相似三角形对应边成比例,可以列出比例式求出BD的长.解: (1) ∵△OAC∽△OBD,∠C=∠D,
∴线段OA与线段OB是对应边,
∴△OAC与△OBD的相似比为
(2)∵△OAC∽△OBD,
相似三角形的定义具有两重性,即:若两个三角形的各角对应相等且各边对应成比例,则这两个三角形相似;反之,若两个三角形相似,则它们的对应角相等且对应边成比例.因此相似三角形的定义既是相似三角形的性质,也是相似三角形的判定方法.警示:求相似比时,不要忽视相似比的顺序性.下列说法中错误的是( )
A.两个全等三角形一定相似
B.两个直角三角形一定相似
C.两个相似三角形的对应角相等,对应边成比例
D.相似的两个三角形不一定全等如图,△ABC∽△DEF,相似比为 1∶2. 若
BC=1,则EF的长是( )
A.1 B.2 C.3 D.42知识点平行线判定两三角形相似 如图,在△ABC中,D为边AB上的任一点,作DE∥BC,交边AC于点E,用刻度尺和量角器量一量,看看△ADE与△ABC的边角之间有什么关系,进而判断这两个三角形是否相似.做一做 显然,∠ADE=∠ABC,∠AED=
∠ACB,∠A=∠A.
又由平行线分线段成比例的基本事
实,可推得 通过度量,还可
以发现 因而有△ADE∽△ABC.
我们可以用演绎推理证明这一结论. 过点D作AC的平行线交BC于点F,
∴ (平行线分线段成比例),
∴
∴
已知:如图,DE∥BC,并分别交AB、AC于点D、E.
求证:△ADE∽△ABC.证明:∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
(平行线分线段成比例),∴△ADE∽△ABC(相似三角形的定义).∵DE∥BC,DF∥AC,
∴四边形DFCE是平行四边形,
∴DE=FC.
∴
又∵∠ADE=∠B,∠AED=∠C,∠A=∠A,用平行线判定三角形相似的定理:平行于三角形一边的直线,和其他两边(或两边的延长线)相交所构成的三角形与原三角形相似.
数学表达式:如图,∵DE∥BC ∴△ABC∽△ADE.要点精析:(1) 定理中“和其他两边相交”是指和其他两边所在直线相交.
(2) 根据定理得到的相似三角形的三个基本图形中都有
BC∥DE,图(1)(2)很像大写字母A,故我们称之为“A”型相似;图(3)很像大写字母X,故我们称之为“X”型相似(也像阿拉伯数字“8”).2、作用:本定理是相似三角形判定定理的预备定理:它通过平行证三角形相似,再由相似证对应角相等、对应边成比例.例2 如图,在△ABC中,点D是边AB的三等分点,
DE∥BC,DE=5.求BC的长.
解:∵DE∥BC,
∴△ADE∽△ABC(平行于三角形
一边的直线,和其他两边相交所
构成的三角形和原三角形相似),
∴
∴BC=3DE=15.利用证三角形相似求线段的长的方法:当三角形被平行线所截形成“A”型或“X”型的图形,并且所求的线段或已知线段在平行的边上,通常考虑通过证三角形相似,再利用相似三角形的对应边成比例构建包含已知与未知线段的比例式,即可求出线段的长.如图,点P是平行四边形ABCD的边AB上一点,
射线CP交DA的延长线于点E,则图中相似的三
角形有( )
A.0对
B.1对
C.2对
D.3对在△ABC中,DE∥BC,AE∶EC=2∶3,DE
=4,则BC等于( )
A.10 B.8 C.9 D.6 利用平行线证比例式或等积式的方法:当比例式或等积式中的线段不在平行线上时,可直接利用平行线分线段成比例定理证明;当比例式或等积式中的线段有的在平行线上时,可直接利用平行线截三角形相似的对应边成比例证明;当比例式或等积式中的线段不是对应线段时,利用转化思想,用等线段、等比例、等积替换进行论证.
