23.3.3 相似三角形的性质 课件(15张PPT)
文档属性
| 名称 | 23.3.3 相似三角形的性质 课件(15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 371.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-16 16:21:16 | ||
图片预览






文档简介
课件15张PPT。第23章 图形的相似23.3 相似三角形相似三角形的性质相似三角形对应线段的比
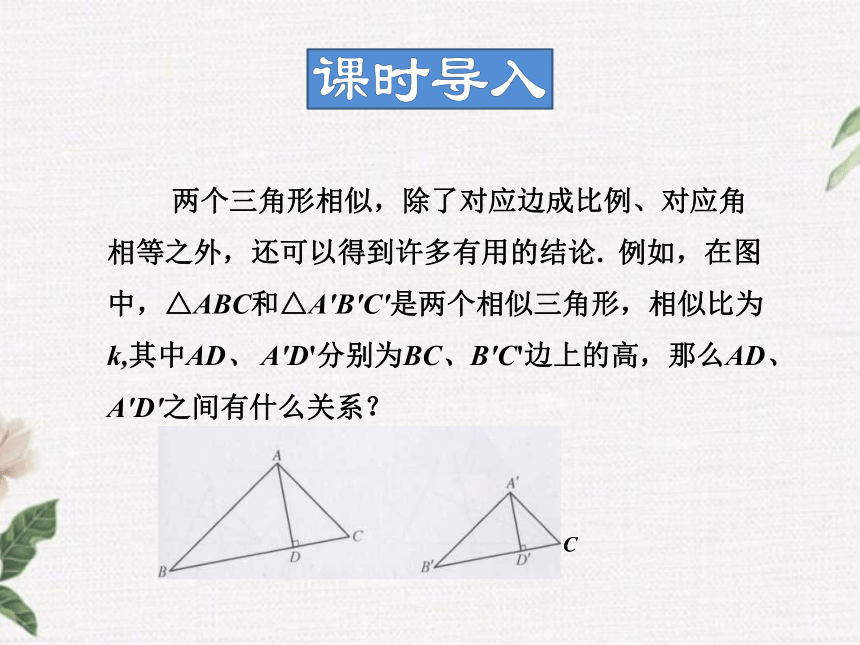
相似三角形的周长的比、面积的比 两个三角形相似,除了对应边成比例、对应角相等之外,还可以得到许多有用的结论. 例如,在图中,△ABC和△A'B'C'是两个相似三角形,相似比为k,其中AD、 A'D'分别为BC、B'C'边上的高,那么AD、A'D'之间有什么关系? 1知识点相似三角形对应线段的比 △ABD和△A'B ' D'都是直角三角形,且∠B
=∠B',因为有两个角对应相等,所以这两个三角
形相似. 因此 如图, △ABC和△A'B'C'相似,AD、A'D'分别为对应边上的中线,BE、B'E'分别为对应角的平分线,
那么它们之间是否有与对应边上的高类似的关系?这两个三角形的周长又有什么关系呢? 思 考:1. 相似三角形对应边上的高的比等于相似比.
2. 相似三角形对应边上的中线的比等于相似比.
3. 相似三角形对应角的平分线的比等于相似比.请你试着证明这些结论易错警示:利用相似三角形的性质时,要注意“对应”两字,要找准对应线段.例1 如图,在△ABC中,DE∥BC,AF为高,
AD∶AB=1∶3,所以AG∶AF= ________.导引:因为DE∥BC,
所以△ADE∽△ABC,
又AF为△ABC的高,
所以AG是△ADE的高,
所以1:3 先证明两个三角形相似,再利用“相似三角
形对应边上的高的比等于相似比”求解.已知△ABC∽△DEF,若△ABC与△DEF的相似比为2∶3,则△ABC与△DEF对应边上的中线的比为________.如图,矩形EFGH内接于△ABC,且边FG落在BC上,若BC=3,AD=2,
EF= EH,那么EH的长
为________.2知识点相似三角形的周长的比、面积的比1. 相似三角形的周长之比等于相似比;
2.相似三角形面积的比等于相似比的平方;
反之,相似三角形的相似比等于面积比的算术平方根.
易错警示:在利用相似三角形的性质解决问题时,常出现面积比等于相似比或由面积比求相似比时不进行开方,反而平方的错误.为了避免这些错误,在利用相似三角形的性质解题时,一定要注意结合图形,搞清面积比与相似比的关系.请你试着证明这些结论(1)求△BEF与△AFD的周长之比,先判定这两个三角形相似,然后找它们的相似比;
(2)在(1)的条件下,利用面积比等于相似比的平方即可求解.例2 已知:如图,□ ABCD中,E是BC边上一点,且
BE= EC,BD,AE相交于F点.
(1)求△BEF的周长与△AFD
的周长之比;
(2)若△BEF的面积为6 cm2,求△AFD的面积.导引:解:(1)∵四边形ABCD是平行四边形,
∴BC∥AD,BC=AD.∴△BEF∽△DAF.
∵BE= EC,
∴BE∶DA=BE∶BC=1∶3.
∴△BEF的周长与△AFD的周长之比为1∶3.
(2)由(1)可知△BEF与△AFD的相似比为
∴S△BEF∶S△AFD=1∶9.
又∵S△BEF=6 cm2,∴S△AFD=54 cm2. 利用相似比求周长和面积时,先判定两个三角形相似,然后找准相似比,利用“相似三角形的周长之比等于相似比,相似三角形面积的比等于相似比的平方”解题.
警示:不要误认为面积的比等于相似比.如果两个相似三角形对应边的比为2∶3,那么这
两个相似三角形面积的比是( )
A.2∶3 B.
C.4∶9 D.8∶27
两个相似三角形的相似比为3∶2,面积之差为
25 cm2,求这两个相似三角形的面积. 用相似三角形对应边上的高的比解决三角形内
接四边形问题应掌握两点:
1.常见图形:如右图,即三角形中存在一个矩形.
2.基本方法:利用相似三角形对应边上的高的比等
于相似比列方程求解.
相似三角形的周长的比、面积的比 两个三角形相似,除了对应边成比例、对应角相等之外,还可以得到许多有用的结论. 例如,在图中,△ABC和△A'B'C'是两个相似三角形,相似比为k,其中AD、 A'D'分别为BC、B'C'边上的高,那么AD、A'D'之间有什么关系? 1知识点相似三角形对应线段的比 △ABD和△A'B ' D'都是直角三角形,且∠B
=∠B',因为有两个角对应相等,所以这两个三角
形相似. 因此 如图, △ABC和△A'B'C'相似,AD、A'D'分别为对应边上的中线,BE、B'E'分别为对应角的平分线,
那么它们之间是否有与对应边上的高类似的关系?这两个三角形的周长又有什么关系呢? 思 考:1. 相似三角形对应边上的高的比等于相似比.
2. 相似三角形对应边上的中线的比等于相似比.
3. 相似三角形对应角的平分线的比等于相似比.请你试着证明这些结论易错警示:利用相似三角形的性质时,要注意“对应”两字,要找准对应线段.例1 如图,在△ABC中,DE∥BC,AF为高,
AD∶AB=1∶3,所以AG∶AF= ________.导引:因为DE∥BC,
所以△ADE∽△ABC,
又AF为△ABC的高,
所以AG是△ADE的高,
所以1:3 先证明两个三角形相似,再利用“相似三角
形对应边上的高的比等于相似比”求解.已知△ABC∽△DEF,若△ABC与△DEF的相似比为2∶3,则△ABC与△DEF对应边上的中线的比为________.如图,矩形EFGH内接于△ABC,且边FG落在BC上,若BC=3,AD=2,
EF= EH,那么EH的长
为________.2知识点相似三角形的周长的比、面积的比1. 相似三角形的周长之比等于相似比;
2.相似三角形面积的比等于相似比的平方;
反之,相似三角形的相似比等于面积比的算术平方根.
易错警示:在利用相似三角形的性质解决问题时,常出现面积比等于相似比或由面积比求相似比时不进行开方,反而平方的错误.为了避免这些错误,在利用相似三角形的性质解题时,一定要注意结合图形,搞清面积比与相似比的关系.请你试着证明这些结论(1)求△BEF与△AFD的周长之比,先判定这两个三角形相似,然后找它们的相似比;
(2)在(1)的条件下,利用面积比等于相似比的平方即可求解.例2 已知:如图,□ ABCD中,E是BC边上一点,且
BE= EC,BD,AE相交于F点.
(1)求△BEF的周长与△AFD
的周长之比;
(2)若△BEF的面积为6 cm2,求△AFD的面积.导引:解:(1)∵四边形ABCD是平行四边形,
∴BC∥AD,BC=AD.∴△BEF∽△DAF.
∵BE= EC,
∴BE∶DA=BE∶BC=1∶3.
∴△BEF的周长与△AFD的周长之比为1∶3.
(2)由(1)可知△BEF与△AFD的相似比为
∴S△BEF∶S△AFD=1∶9.
又∵S△BEF=6 cm2,∴S△AFD=54 cm2. 利用相似比求周长和面积时,先判定两个三角形相似,然后找准相似比,利用“相似三角形的周长之比等于相似比,相似三角形面积的比等于相似比的平方”解题.
警示:不要误认为面积的比等于相似比.如果两个相似三角形对应边的比为2∶3,那么这
两个相似三角形面积的比是( )
A.2∶3 B.
C.4∶9 D.8∶27
两个相似三角形的相似比为3∶2,面积之差为
25 cm2,求这两个相似三角形的面积. 用相似三角形对应边上的高的比解决三角形内
接四边形问题应掌握两点:
1.常见图形:如右图,即三角形中存在一个矩形.
2.基本方法:利用相似三角形对应边上的高的比等
于相似比列方程求解.
