24.2 直角三角形的性质 课件(21张PPT)
文档属性
| 名称 | 24.2 直角三角形的性质 课件(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 446.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-16 00:00:00 | ||
图片预览








文档简介
课件21张PPT。第二十四章 解直角三角形24.2 直角三角形的性质直角三角形斜边上的中线的性质
直角三角形30°角的性质 在研究直角三角形的边角关系之前,我们先来探索和归纳直角三角形的性质.
我们已经知道:
(1)直角三角形的两个锐角互余.
(2)直角三角形两直角边的平方和等于斜边的平方 (勾股
定理).
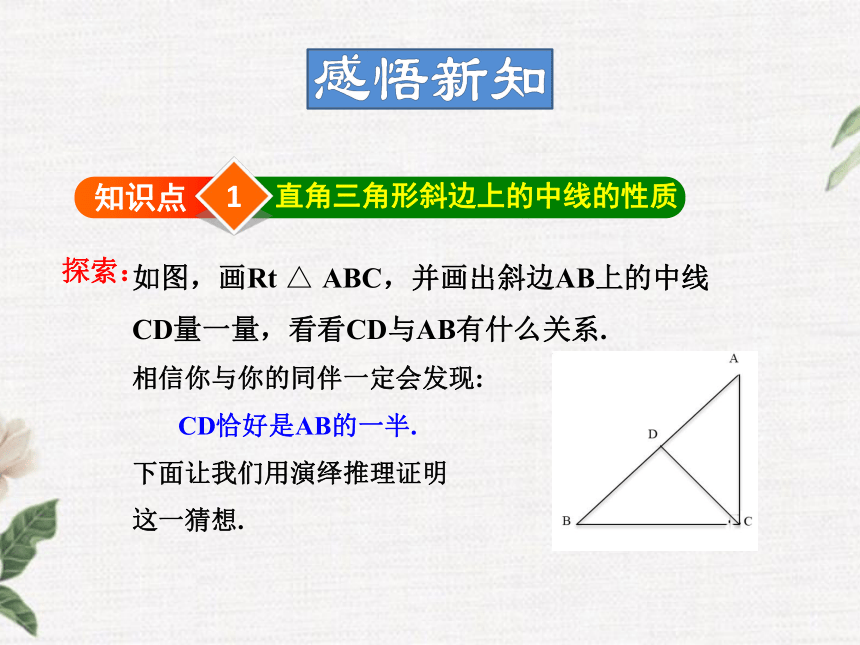
下面我们探索直角三角形的其他性质.1知识点直角三角形斜边上的中线的性质探索:如图,画Rt △ ABC,并画出斜边AB上的中线CD量一量,看看CD与AB有什么关系.
相信你与你的同伴一定会发现:
CD恰好是AB的一半.
下面让我们用演绎推理证明
这一猜想.已知:如图 ,在 Rt ABC 中, ∠ ACB= 90 °, CD是斜边AB上的中线. 求证:CD = AB
证明:延长CD至点E,使DE= CD,连结AE、BE
∵CD是斜边AB上的中线,
∴AD = DB.又∵ DE = CD,
∴四边形ACBE是平行四边形.
又∵ ∠ ACB=90°,
∴四边形ACBE是矩形,
∴ CE = AB,
∴ CD = CE = AB. 直角三角形斜边上的中线等于斜边的一半,是直角三角形的又一条性质,它表述了直角三角形斜边上的中线与斜边之间的关系.【例1】 〈山东枣庄〉如图24.2-1,△ABC中,AB=AC
=10,BC=8,AD平分∠BAC交BC于点D,
点E为AC的中点,连结DE,则△CDE的周长
为( )
A.20 B.12 C.14 D.13导引:根据等腰三角形三线合一的性质可得
AD⊥BC,CD=BD,再根据直角三角
形斜边上的中线等于斜边的一半可得
DE=CE= AC,然后根据三角形的周
长公式列式计算即可得解.∵AB=AC,AD平分∠BAC,BC=8,∴AD⊥BC,CD=BD= BC=4,
又∵点E为AC的中点,∴DE=CE= AC=5,∴△CDE的周长=CD+DE+CE=4+5+5=14.故选C.
答案:C 本题采用了数形结合思想,考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形三线合一的性质,熟记性质并准确识图是解题的关键.
(2015·北京)如图,公路AC,BC互相垂直,公路
AB的中点M与点C被湖隔开,若测得AM的长为
1.2 km,则M,C两点间的距离为( )
A.0.5 km B.0.6 km
C.0.9 km D.1.2 km
2 (2015·德阳)如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,若点A关于CD所在直线的对称点E恰好为AB的中点,则∠B的度数是( )
A.60° B.45° C.30° D.75°
2知识点直角三角形30°角的性质【例2】 如图,在Rt△ABC中, ∠ACB=90°,
∠A= 30 °.求证:BC =利用直角三角形的上述性质,可以解决某些与
直角三角形有关的问题.证明:作斜边AB上的中线CD,则
∵∠A=30°,
∴∠B=60°,
∴△CDB是等边三角形.
∴BC=BD=
1. 在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.本性质是用角的特殊性来揭示直角三角形中直角边与斜边的数量关系的.
2.拓展:直角三角形的性质的选用
(1) 在直角三角形中求角时,常用“直角三角形的两个锐角互余”.
(2) 当已知直角三角形斜边上的中线时,常用“直角三角形斜边上的中线等于斜边的一半”.(3) 当已知直角三角形中一个锐角为30°时,常用“30°角所对的直角边等于斜边的一半”.反之,若已知一条直角边等于斜边的一半,我们可以得到这条直角边所对的锐角为30°,实现了边、角之间的转化.
(4) 当已知直角三角形中两边的长求第三边时,我们选用勾股定理.【例3】 如图24.2-5,测量旗杆AB的高度时,先在地面上选
择一点C,使∠ACB=15°,然后朝着旗杆方向前
进到点D,测得∠ADB=30°,量得CD=13 m,
求旗杆AB的高度.导引:根据三角形的一个外角等于
与它不相邻的两个内角的和
求出∠CAD的度数,再根据等角对等边的性
质可得AD=CD,然后根据直角三角形中
30°角所对的直角边等于斜边的一半解答即可.解: ∵∠ACB=15°,∠ADB=30°,
∴∠CAD=∠ADB-∠ACB=30°-15°=15°,
∴∠ACB=∠CAD,∴AD=CD=13 m.
在△ADB中,
∵AB⊥DB,∠ADB=30°,
在含30°角的直角三角形中求线段的长度,要注意利用直角三角形中30°角所对的直角边等于斜边的一半的性质. (黄冈)如图,在△ABC中,∠C=90°,
∠B=30°,边AB的垂直平分线DE交AB于点E,
交BC于点D,CD=3,则BC的长为( )
A.6 B.6 C.9 D.3(眉山)如图,在Rt△ABC中,∠B=90°,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD.若BD=1,则AC的长是( )
A.2 B.2 C.4 D.4 在直角三角形中,若遇到中点问题,常考虑作斜边上的中线,利用斜边上的中线等于斜边的一半构造等腰三角形,把问题转化为等腰三角形问题来解决;若遇到含30°角或60°角问题常考虑构造含30°角的直角三角形来解决相关问题.
直角三角形30°角的性质 在研究直角三角形的边角关系之前,我们先来探索和归纳直角三角形的性质.
我们已经知道:
(1)直角三角形的两个锐角互余.
(2)直角三角形两直角边的平方和等于斜边的平方 (勾股
定理).
下面我们探索直角三角形的其他性质.1知识点直角三角形斜边上的中线的性质探索:如图,画Rt △ ABC,并画出斜边AB上的中线CD量一量,看看CD与AB有什么关系.
相信你与你的同伴一定会发现:
CD恰好是AB的一半.
下面让我们用演绎推理证明
这一猜想.已知:如图 ,在 Rt ABC 中, ∠ ACB= 90 °, CD是斜边AB上的中线. 求证:CD = AB
证明:延长CD至点E,使DE= CD,连结AE、BE
∵CD是斜边AB上的中线,
∴AD = DB.又∵ DE = CD,
∴四边形ACBE是平行四边形.
又∵ ∠ ACB=90°,
∴四边形ACBE是矩形,
∴ CE = AB,
∴ CD = CE = AB. 直角三角形斜边上的中线等于斜边的一半,是直角三角形的又一条性质,它表述了直角三角形斜边上的中线与斜边之间的关系.【例1】 〈山东枣庄〉如图24.2-1,△ABC中,AB=AC
=10,BC=8,AD平分∠BAC交BC于点D,
点E为AC的中点,连结DE,则△CDE的周长
为( )
A.20 B.12 C.14 D.13导引:根据等腰三角形三线合一的性质可得
AD⊥BC,CD=BD,再根据直角三角
形斜边上的中线等于斜边的一半可得
DE=CE= AC,然后根据三角形的周
长公式列式计算即可得解.∵AB=AC,AD平分∠BAC,BC=8,∴AD⊥BC,CD=BD= BC=4,
又∵点E为AC的中点,∴DE=CE= AC=5,∴△CDE的周长=CD+DE+CE=4+5+5=14.故选C.
答案:C 本题采用了数形结合思想,考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形三线合一的性质,熟记性质并准确识图是解题的关键.
(2015·北京)如图,公路AC,BC互相垂直,公路
AB的中点M与点C被湖隔开,若测得AM的长为
1.2 km,则M,C两点间的距离为( )
A.0.5 km B.0.6 km
C.0.9 km D.1.2 km
2 (2015·德阳)如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,若点A关于CD所在直线的对称点E恰好为AB的中点,则∠B的度数是( )
A.60° B.45° C.30° D.75°
2知识点直角三角形30°角的性质【例2】 如图,在Rt△ABC中, ∠ACB=90°,
∠A= 30 °.求证:BC =利用直角三角形的上述性质,可以解决某些与
直角三角形有关的问题.证明:作斜边AB上的中线CD,则
∵∠A=30°,
∴∠B=60°,
∴△CDB是等边三角形.
∴BC=BD=
1. 在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.本性质是用角的特殊性来揭示直角三角形中直角边与斜边的数量关系的.
2.拓展:直角三角形的性质的选用
(1) 在直角三角形中求角时,常用“直角三角形的两个锐角互余”.
(2) 当已知直角三角形斜边上的中线时,常用“直角三角形斜边上的中线等于斜边的一半”.(3) 当已知直角三角形中一个锐角为30°时,常用“30°角所对的直角边等于斜边的一半”.反之,若已知一条直角边等于斜边的一半,我们可以得到这条直角边所对的锐角为30°,实现了边、角之间的转化.
(4) 当已知直角三角形中两边的长求第三边时,我们选用勾股定理.【例3】 如图24.2-5,测量旗杆AB的高度时,先在地面上选
择一点C,使∠ACB=15°,然后朝着旗杆方向前
进到点D,测得∠ADB=30°,量得CD=13 m,
求旗杆AB的高度.导引:根据三角形的一个外角等于
与它不相邻的两个内角的和
求出∠CAD的度数,再根据等角对等边的性
质可得AD=CD,然后根据直角三角形中
30°角所对的直角边等于斜边的一半解答即可.解: ∵∠ACB=15°,∠ADB=30°,
∴∠CAD=∠ADB-∠ACB=30°-15°=15°,
∴∠ACB=∠CAD,∴AD=CD=13 m.
在△ADB中,
∵AB⊥DB,∠ADB=30°,
在含30°角的直角三角形中求线段的长度,要注意利用直角三角形中30°角所对的直角边等于斜边的一半的性质. (黄冈)如图,在△ABC中,∠C=90°,
∠B=30°,边AB的垂直平分线DE交AB于点E,
交BC于点D,CD=3,则BC的长为( )
A.6 B.6 C.9 D.3(眉山)如图,在Rt△ABC中,∠B=90°,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD.若BD=1,则AC的长是( )
A.2 B.2 C.4 D.4 在直角三角形中,若遇到中点问题,常考虑作斜边上的中线,利用斜边上的中线等于斜边的一半构造等腰三角形,把问题转化为等腰三角形问题来解决;若遇到含30°角或60°角问题常考虑构造含30°角的直角三角形来解决相关问题.
