人教版高一数学函数的最值问题-教案
文档属性
| 名称 | 人教版高一数学函数的最值问题-教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-17 00:00:00 | ||
图片预览




文档简介
适用学科
高中数学
适用年级
高一
适用区域
人教版区域
课时时长(分钟)
2课时
知识点
单调性的应用,最值问题
教学目标
使学生理解函数的最值是在整个定义域上来研究的,是函数单调性的应用.
通过渗透数形结合的思想方法,掌握求函数最值的方法.
教学重点
函数最大(小)值的定义和求法.
教学难点
如何求一个具体函数的最值.
【教学建议】
函数的最大(小)值的定义,是借助于二次函数及其图像引出的,概念的出现仍然是遵循特殊到一般的原则.鉴于学生对于二次函数已经有了一个初步的了解,因此本节课多从学生接触过的二次函数入手,这样能使学生容易找到最高点和最低点.但这只是感性上的认识,要培养学生能用数学语言描述函数最值的概念,通过对概念的辨析,真正让学生理解最值概念的内涵,同时,在做题时多培养学生画图的能力,体会到数形结合的魅力.
【知识导图】
【教学建议】
导入是一节课必备的一个环节,是为了激发学生的学习兴趣,帮助学生尽快进入学习状态。
导入的方法很多,仅举两种方法:
情境导入,比如讲一个和本讲内容有关的生活现象;
温故知新,在知识体系中,从学生已有知识入手,揭示本节知识与旧知识的关系,帮学生建立知识网络。
提供一个教学设计供讲师参考:
(1)由于某种原因,2008年北京奥运会开幕式时间由原定的7月25日推迟到8月8日,请查阅资料说明做出这个决定的主要原因.
(2)通过查阅历史资料研究北京奥运会开幕式当天气温变化情况.
课上通过交流,可以了解到开幕式推迟主要是天气的原因,北京的天气到8月中旬,平均气温、平均降雨量和平均降雨天数等均开始下降,比较适宜举办大型国际体育赛事.下图是北京市某年8月8日一天24小时内气温随时间变化的曲线图.
问题:观察图形,能得到什么信息?
预案:(1)当天最高温度、最低温度是多少以及何时达到;
(2)在某时刻的温度;
(3)某些时段温度升高,某些时段温度降低.
在生活中,我们关心很多数据的变化规律,了解这些数据的变化规律,对我们的生活是很有帮助的.
问题:还能举出生活中其他的数据变化情况吗?
预案:水位高低、燃油价格、股票价格等.
设计意图:用函数观点看,其实就是随着自变量的变化,函数值是变大还是变小.从而引入最大值、最小值的概念.
【教学建议】通过前面的引导,得到函数最值的定义,建议老师在引导学生得到最大值的定义以后,可以让学生来类比写出最小值的定义:
前提
设函数的定义域为,如果存在实数满足
条件
①对于任意,都有;
②存在,使得
①对于任意,都有;
②存在,使得
结论
M为最大值
M为最小值
函数图象上任意点的坐标的意义:横坐标是自变量的取值,纵坐标是自变量为时对应的函数值的大小.
(1)图象上最高点的纵坐标是所有函数值中的最大值,即函数的最大值.
(2)由于点C是函数图象上的最高点,则点A在点C的下方,即对定义域内任意,都有,即,也就是对函数的定义域内任意,均有成立.
(3)一般地,设函数的定义域为,如果存在实数满足:
①对于任意的,都有;
②存在,使得.
那么,称是函数的最大值.
(4) 反映了函数的所有函数值不大于实数;这个函数的特征是图象有最高点,并且最高点的纵坐标是.
(5)函数,没有最大值,因为函数,的图象没有最高点.
(6)讨论函数的最大值,要坚持定义域优先的原则;函数图象上有最高点时,这个函数才存在最大值,最高点必须是函数图象上的点.
考点3函数的最小值
(1)函数最小值的定义是:
一般地,设函数的定义域为,如果存在实数满足:
①对于任意的,都有;
②存在,使得.
那么,称是函数的最小值。
函数最小值的几何意义:函数图象上最低点的纵坐标.
(2)讨论函数的最小值,也要坚持定义域优先的原则;函数图象上有最低点时,这个函数才存在最小值,最低点必须是函数图象上的点.
类型一:单调区间的判断并求最值
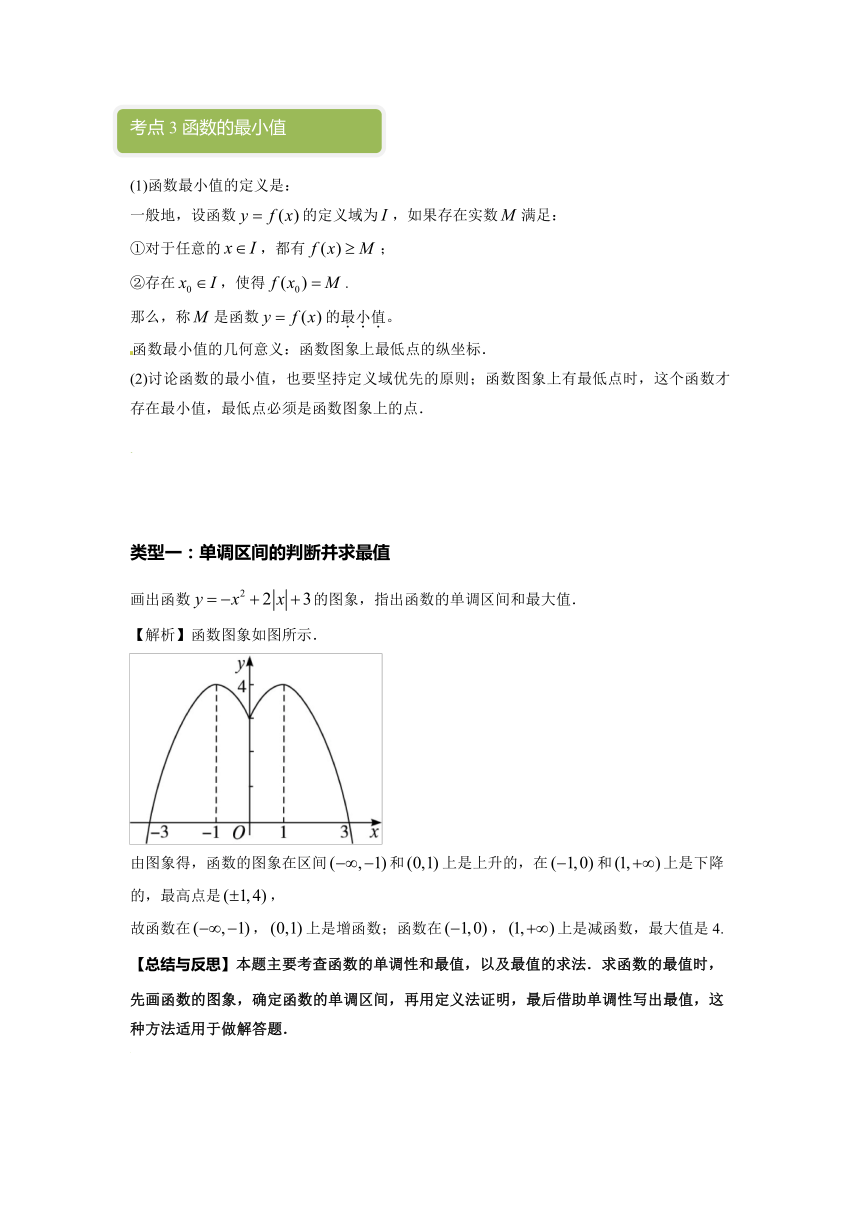
画出函数的图象,指出函数的单调区间和最大值.
【解析】函数图象如图所示.
由图象得,函数的图象在区间和上是上升的,在和上是下降的,最高点是,
故函数在,上是增函数;函数在,上是减函数,最大值是4.
【总结与反思】本题主要考查函数的单调性和最值,以及最值的求法.求函数的最值时,先画函数的图象,确定函数的单调区间,再用定义法证明,最后借助单调性写出最值,这种方法适用于做解答题.
求函数在区间上的最大值和最小值.
【解析】设,则有 .
∵,∴,.
∴,即函数在区间上是减函数.
∴当时,函数在区间上取得最大值;
当时,函数在区间上取得最小值.
【总结与反思】
单调法求函数最值:先判断函数的单调性,再利用其单调性求最值;
常用到下面的结论:
①如果函数在区间上单调递增,在区间上单调递减,则函数在处有最大值;
②如果函数在区间上单调递减,在区间上单调递增,则函数在处有最小值.
已知函数对于任意,总有,且当时,, .
(1)求证:在上是减函数;
(2) 求在上的最大值和最小值.
【解析】(1)方法一:∵函数对于任意,总有,
令,得.再令,得.在上任取,则,,
又∵时,.而,∴.因此在上是减函数.
方法二:在上任取,,不妨设,
则,
又∵时,,而,
∴,即.
因此在上是减函数.
(2)∵在上为减函数,
∴在上也为减函数,
∴在上的最大值为、最小值为,
而,∵,
∴,
因此,在上的最大值为2,最小值为-2.
类型二最值的应用
“菊花”烟花是最壮观的烟花之一.制造时一般是期望在它达到最高点时爆裂.如果烟花距地面的高度与时间之间的关系为,那么烟花冲出后什么时候是它爆裂的最佳时刻?这时距地面的高度是多少?(精确到)
【解析】作出函数的图象,如图所示,
显然,函数图象的顶点就是烟花上升的最高点,顶点的横坐标就是烟花爆裂的最佳时刻,纵坐标就是这时距地面的高度.
由二次函数的知识,对于函数,我们有:
当时,函数有最大值.
即烟花冲出后是它爆裂的最佳时刻,这时距地面的高度约是.
【总结与反思】
本题主要考查二次函数的最值问题,以及应用二次函数解决实际问题的能力.
解应用题的步骤是:
(1)审清题意读懂题;(2)将实际问题转化为数学问题来解决;(3)归纳结论.
注意:要坚持定义域优先的原则;求二次函数的最值要借助于图象即数形结合.
1. 函数在区间上的最大值是_________,最小值是_______.
2. 将进货单价40元的商品按50元一个售出时,能卖出500个,若此商品每个涨价1元,其销售量减少10个,为了赚到最大利润,售价应定为多少?
3.函数的最大值是( )
A. B. C. D.
答案与解析
1.【答案】
【解析】函数是定义在区间上的二次函数,其对称轴方程是,顶点坐标为,且其图象开口向下,显然其顶点横坐标在上,
如图所示,函数的最大值为,最小值为.
2. 【答案】为了赚取最大利润,售价应定为70元
【解析】设利润为元,每个售价为元,则每个涨元,从而销售量减少 个,共售出个
∴
∴时,元
3. 【答案】D
【解析】,所以当时有最大值.
1.已知,求函数的最值.
2.求函数的最大值.
3.如果函数定义在区间上,求的最小值.
4.求在区间上的最大值.
答案与解析
1.【答案】
【解析】由已知,可得,即函数是定义在区间上的二次函数.将二次函数配方得,其对称轴方程,顶点坐标,且图象开口向上.显然其顶点横坐标不在区间内,如图所示。函数的最小值为,最大值为.
2.【答案】
【解析】令 有,则 ,
3.【答案】
【解析】函数,其对称轴方程为,顶点坐标为,图象开口向上.
如图1所示,若顶点横坐标在区间左侧时,有,此时,当时,函数取得最小值.
图1
如图2所示,若顶点横坐标在区间上时,有,即。当时,函数取得最小值.
图2
如图3所示,若顶点横坐标在区间右侧时,有,即。当时,函数取得最小值.
综上讨论,
图3
4.【答案】
【解析】二次函数的对称轴方程为,
当即时,;
当即时,
综上所述:
1. 已知,求的最小值.
2. 已知函数在区间上的最大值为4,求实数的值.
答案与解析
1.【答案】
【解析】将代入中,得
,即时,
,即时,
所以 .
2.【答案】或
【解析】
(1)若,不符合题意.
(2)若则,由,得.
(3)若时,则,由,得.
综上知或.
本节讲了2个重要内容:
(1)最值的定义:设函数的定义域为,如果存在实数满足:对于任意的,都有;存在,使得. 那么,称是函数的最大值. 仿照最大值定义,可以给出最小值的定义.
(2)最值的常用求法
①配方法:研究二次函数的最大(小)值,当定义域为R时,先配方成后,当时,函数取最小值为;当时,函数取最大值.
②单调法:一些函数的单调性,比较容易观察出来,或者可以先证明出函数的单调性,再利用函数的单调性求函数的最大值或最小值.
③图象法:先作出其函数图象后,然后观察图象得到函数的最大值或最小值.
1. 抛物线,当= _____ 时,图象的顶点在轴上;当= _____ 时,图象的顶点在轴上;当= _____ 时,图象过原点.
2. 用一长度为米的铁丝围成一个长方形或正方形,则其所围成的最大面积为 ________
3. 某商场以每件30元的价格购进一种商品,试销中发现这种商品每天的销售量(件)与每件的销售价(元)满足一次函数.
(1) 写出商场卖这种商品每天的销售利润与每件销售价之间的函数关系式;
(2) 若商场要想每天获得最大销售利润,每件商品的售价定为多少最合适?最大销售利润为多少?
答案与解析
1.【答案】4,14或2,
2.【答案】.
3.【答案】(1);
(2) 售价定为42元时每天有最大销售利润,最大销售利润为432元.
【解析】(1) 由已知得每件商品的销售利润为元,
那么件的销售利润为,又.
(2) 由(1)知对称轴为,位于的范围内,另抛物线开口向下
当时,
当每件商品的售价定为42元时每天有最大销售利润,最大销售利润为432元.
1. 已知,且,求函数的最值.
2. 已知,当时,求的最大值.
3. 求函数在上的最大值.
答案与解析
1.【答案】函数的最小值是,最大值是.
【解析】由已知有,于是函数是定义在区间上的二次函数,将配方得:.
二次函数的对称轴方程是顶点坐标为,图象开口向上
由可得,显然其顶点横坐标在区间的左侧或左端点上.
函数的最小值是,最大值是.
2.【答案】
【解析】:由已知可求对称轴为.
(1)当时,.
(2)当,即时,.
根据对称性,若即时,.
若即时,.
(3)当即时,.
综上,
3.【答案】
【解析】函数图象的对称轴方程为,应分,,即,和这三种情形讨论,下列三图分别为
(1);由图可知
(2);由图可知
(3) 时;由图可知
;即
已知函数在区间上的最小值是最大值是,求,的值.
已知的值域为,求函数的值域.
答案与解析
1.【答案】
【解析】讨论对称轴中 与的位置关系。
①若,则,解得
②若,则,无解
③若,则,无解
④若,则,无解
综上,.
2.【答案】
【解析】令,得.
由于,得.因此.
.
当时有最小值;当时有最大值.
故的值域为.
高中数学
适用年级
高一
适用区域
人教版区域
课时时长(分钟)
2课时
知识点
单调性的应用,最值问题
教学目标
使学生理解函数的最值是在整个定义域上来研究的,是函数单调性的应用.
通过渗透数形结合的思想方法,掌握求函数最值的方法.
教学重点
函数最大(小)值的定义和求法.
教学难点
如何求一个具体函数的最值.
【教学建议】
函数的最大(小)值的定义,是借助于二次函数及其图像引出的,概念的出现仍然是遵循特殊到一般的原则.鉴于学生对于二次函数已经有了一个初步的了解,因此本节课多从学生接触过的二次函数入手,这样能使学生容易找到最高点和最低点.但这只是感性上的认识,要培养学生能用数学语言描述函数最值的概念,通过对概念的辨析,真正让学生理解最值概念的内涵,同时,在做题时多培养学生画图的能力,体会到数形结合的魅力.
【知识导图】
【教学建议】
导入是一节课必备的一个环节,是为了激发学生的学习兴趣,帮助学生尽快进入学习状态。
导入的方法很多,仅举两种方法:
情境导入,比如讲一个和本讲内容有关的生活现象;
温故知新,在知识体系中,从学生已有知识入手,揭示本节知识与旧知识的关系,帮学生建立知识网络。
提供一个教学设计供讲师参考:
(1)由于某种原因,2008年北京奥运会开幕式时间由原定的7月25日推迟到8月8日,请查阅资料说明做出这个决定的主要原因.
(2)通过查阅历史资料研究北京奥运会开幕式当天气温变化情况.
课上通过交流,可以了解到开幕式推迟主要是天气的原因,北京的天气到8月中旬,平均气温、平均降雨量和平均降雨天数等均开始下降,比较适宜举办大型国际体育赛事.下图是北京市某年8月8日一天24小时内气温随时间变化的曲线图.
问题:观察图形,能得到什么信息?
预案:(1)当天最高温度、最低温度是多少以及何时达到;
(2)在某时刻的温度;
(3)某些时段温度升高,某些时段温度降低.
在生活中,我们关心很多数据的变化规律,了解这些数据的变化规律,对我们的生活是很有帮助的.
问题:还能举出生活中其他的数据变化情况吗?
预案:水位高低、燃油价格、股票价格等.
设计意图:用函数观点看,其实就是随着自变量的变化,函数值是变大还是变小.从而引入最大值、最小值的概念.
【教学建议】通过前面的引导,得到函数最值的定义,建议老师在引导学生得到最大值的定义以后,可以让学生来类比写出最小值的定义:
前提
设函数的定义域为,如果存在实数满足
条件
①对于任意,都有;
②存在,使得
①对于任意,都有;
②存在,使得
结论
M为最大值
M为最小值
函数图象上任意点的坐标的意义:横坐标是自变量的取值,纵坐标是自变量为时对应的函数值的大小.
(1)图象上最高点的纵坐标是所有函数值中的最大值,即函数的最大值.
(2)由于点C是函数图象上的最高点,则点A在点C的下方,即对定义域内任意,都有,即,也就是对函数的定义域内任意,均有成立.
(3)一般地,设函数的定义域为,如果存在实数满足:
①对于任意的,都有;
②存在,使得.
那么,称是函数的最大值.
(4) 反映了函数的所有函数值不大于实数;这个函数的特征是图象有最高点,并且最高点的纵坐标是.
(5)函数,没有最大值,因为函数,的图象没有最高点.
(6)讨论函数的最大值,要坚持定义域优先的原则;函数图象上有最高点时,这个函数才存在最大值,最高点必须是函数图象上的点.
考点3函数的最小值
(1)函数最小值的定义是:
一般地,设函数的定义域为,如果存在实数满足:
①对于任意的,都有;
②存在,使得.
那么,称是函数的最小值。
函数最小值的几何意义:函数图象上最低点的纵坐标.
(2)讨论函数的最小值,也要坚持定义域优先的原则;函数图象上有最低点时,这个函数才存在最小值,最低点必须是函数图象上的点.
类型一:单调区间的判断并求最值
画出函数的图象,指出函数的单调区间和最大值.
【解析】函数图象如图所示.
由图象得,函数的图象在区间和上是上升的,在和上是下降的,最高点是,
故函数在,上是增函数;函数在,上是减函数,最大值是4.
【总结与反思】本题主要考查函数的单调性和最值,以及最值的求法.求函数的最值时,先画函数的图象,确定函数的单调区间,再用定义法证明,最后借助单调性写出最值,这种方法适用于做解答题.
求函数在区间上的最大值和最小值.
【解析】设,则有 .
∵,∴,.
∴,即函数在区间上是减函数.
∴当时,函数在区间上取得最大值;
当时,函数在区间上取得最小值.
【总结与反思】
单调法求函数最值:先判断函数的单调性,再利用其单调性求最值;
常用到下面的结论:
①如果函数在区间上单调递增,在区间上单调递减,则函数在处有最大值;
②如果函数在区间上单调递减,在区间上单调递增,则函数在处有最小值.
已知函数对于任意,总有,且当时,, .
(1)求证:在上是减函数;
(2) 求在上的最大值和最小值.
【解析】(1)方法一:∵函数对于任意,总有,
令,得.再令,得.在上任取,则,,
又∵时,.而,∴.因此在上是减函数.
方法二:在上任取,,不妨设,
则,
又∵时,,而,
∴,即.
因此在上是减函数.
(2)∵在上为减函数,
∴在上也为减函数,
∴在上的最大值为、最小值为,
而,∵,
∴,
因此,在上的最大值为2,最小值为-2.
类型二最值的应用
“菊花”烟花是最壮观的烟花之一.制造时一般是期望在它达到最高点时爆裂.如果烟花距地面的高度与时间之间的关系为,那么烟花冲出后什么时候是它爆裂的最佳时刻?这时距地面的高度是多少?(精确到)
【解析】作出函数的图象,如图所示,
显然,函数图象的顶点就是烟花上升的最高点,顶点的横坐标就是烟花爆裂的最佳时刻,纵坐标就是这时距地面的高度.
由二次函数的知识,对于函数,我们有:
当时,函数有最大值.
即烟花冲出后是它爆裂的最佳时刻,这时距地面的高度约是.
【总结与反思】
本题主要考查二次函数的最值问题,以及应用二次函数解决实际问题的能力.
解应用题的步骤是:
(1)审清题意读懂题;(2)将实际问题转化为数学问题来解决;(3)归纳结论.
注意:要坚持定义域优先的原则;求二次函数的最值要借助于图象即数形结合.
1. 函数在区间上的最大值是_________,最小值是_______.
2. 将进货单价40元的商品按50元一个售出时,能卖出500个,若此商品每个涨价1元,其销售量减少10个,为了赚到最大利润,售价应定为多少?
3.函数的最大值是( )
A. B. C. D.
答案与解析
1.【答案】
【解析】函数是定义在区间上的二次函数,其对称轴方程是,顶点坐标为,且其图象开口向下,显然其顶点横坐标在上,
如图所示,函数的最大值为,最小值为.
2. 【答案】为了赚取最大利润,售价应定为70元
【解析】设利润为元,每个售价为元,则每个涨元,从而销售量减少 个,共售出个
∴
∴时,元
3. 【答案】D
【解析】,所以当时有最大值.
1.已知,求函数的最值.
2.求函数的最大值.
3.如果函数定义在区间上,求的最小值.
4.求在区间上的最大值.
答案与解析
1.【答案】
【解析】由已知,可得,即函数是定义在区间上的二次函数.将二次函数配方得,其对称轴方程,顶点坐标,且图象开口向上.显然其顶点横坐标不在区间内,如图所示。函数的最小值为,最大值为.
2.【答案】
【解析】令 有,则 ,
3.【答案】
【解析】函数,其对称轴方程为,顶点坐标为,图象开口向上.
如图1所示,若顶点横坐标在区间左侧时,有,此时,当时,函数取得最小值.
图1
如图2所示,若顶点横坐标在区间上时,有,即。当时,函数取得最小值.
图2
如图3所示,若顶点横坐标在区间右侧时,有,即。当时,函数取得最小值.
综上讨论,
图3
4.【答案】
【解析】二次函数的对称轴方程为,
当即时,;
当即时,
综上所述:
1. 已知,求的最小值.
2. 已知函数在区间上的最大值为4,求实数的值.
答案与解析
1.【答案】
【解析】将代入中,得
,即时,
,即时,
所以 .
2.【答案】或
【解析】
(1)若,不符合题意.
(2)若则,由,得.
(3)若时,则,由,得.
综上知或.
本节讲了2个重要内容:
(1)最值的定义:设函数的定义域为,如果存在实数满足:对于任意的,都有;存在,使得. 那么,称是函数的最大值. 仿照最大值定义,可以给出最小值的定义.
(2)最值的常用求法
①配方法:研究二次函数的最大(小)值,当定义域为R时,先配方成后,当时,函数取最小值为;当时,函数取最大值.
②单调法:一些函数的单调性,比较容易观察出来,或者可以先证明出函数的单调性,再利用函数的单调性求函数的最大值或最小值.
③图象法:先作出其函数图象后,然后观察图象得到函数的最大值或最小值.
1. 抛物线,当= _____ 时,图象的顶点在轴上;当= _____ 时,图象的顶点在轴上;当= _____ 时,图象过原点.
2. 用一长度为米的铁丝围成一个长方形或正方形,则其所围成的最大面积为 ________
3. 某商场以每件30元的价格购进一种商品,试销中发现这种商品每天的销售量(件)与每件的销售价(元)满足一次函数.
(1) 写出商场卖这种商品每天的销售利润与每件销售价之间的函数关系式;
(2) 若商场要想每天获得最大销售利润,每件商品的售价定为多少最合适?最大销售利润为多少?
答案与解析
1.【答案】4,14或2,
2.【答案】.
3.【答案】(1);
(2) 售价定为42元时每天有最大销售利润,最大销售利润为432元.
【解析】(1) 由已知得每件商品的销售利润为元,
那么件的销售利润为,又.
(2) 由(1)知对称轴为,位于的范围内,另抛物线开口向下
当时,
当每件商品的售价定为42元时每天有最大销售利润,最大销售利润为432元.
1. 已知,且,求函数的最值.
2. 已知,当时,求的最大值.
3. 求函数在上的最大值.
答案与解析
1.【答案】函数的最小值是,最大值是.
【解析】由已知有,于是函数是定义在区间上的二次函数,将配方得:.
二次函数的对称轴方程是顶点坐标为,图象开口向上
由可得,显然其顶点横坐标在区间的左侧或左端点上.
函数的最小值是,最大值是.
2.【答案】
【解析】:由已知可求对称轴为.
(1)当时,.
(2)当,即时,.
根据对称性,若即时,.
若即时,.
(3)当即时,.
综上,
3.【答案】
【解析】函数图象的对称轴方程为,应分,,即,和这三种情形讨论,下列三图分别为
(1);由图可知
(2);由图可知
(3) 时;由图可知
;即
已知函数在区间上的最小值是最大值是,求,的值.
已知的值域为,求函数的值域.
答案与解析
1.【答案】
【解析】讨论对称轴中 与的位置关系。
①若,则,解得
②若,则,无解
③若,则,无解
④若,则,无解
综上,.
2.【答案】
【解析】令,得.
由于,得.因此.
.
当时有最小值;当时有最大值.
故的值域为.
