人教版数学必修5 3.3.1 二元一次不等式(组)与平面区域(共24张ppt)
文档属性
| 名称 | 人教版数学必修5 3.3.1 二元一次不等式(组)与平面区域(共24张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 296.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-17 00:00:00 | ||
图片预览






文档简介
课件24张PPT。二元一次不等式(组)与平面区域教学目标1、掌握二元一次不等式(组)区域的判断的方法;经历从实际问题抽象出二元一次不等式(组)的过程,能作出二元一次不等式(组)表示的平面区域;
2、经历自主探究分析问题和解决问题的能力;理解数学的转化,数形结合以及分类讨论思想;
3、通过主动参与合作交流,培养团队协作和勇于探索的精神;体会数学的应用价值;体会由特殊到一般的思想。教学重点:
探究特殊二元一次不等式的平面区域。
教学难点:
探究一般二元一次不等式
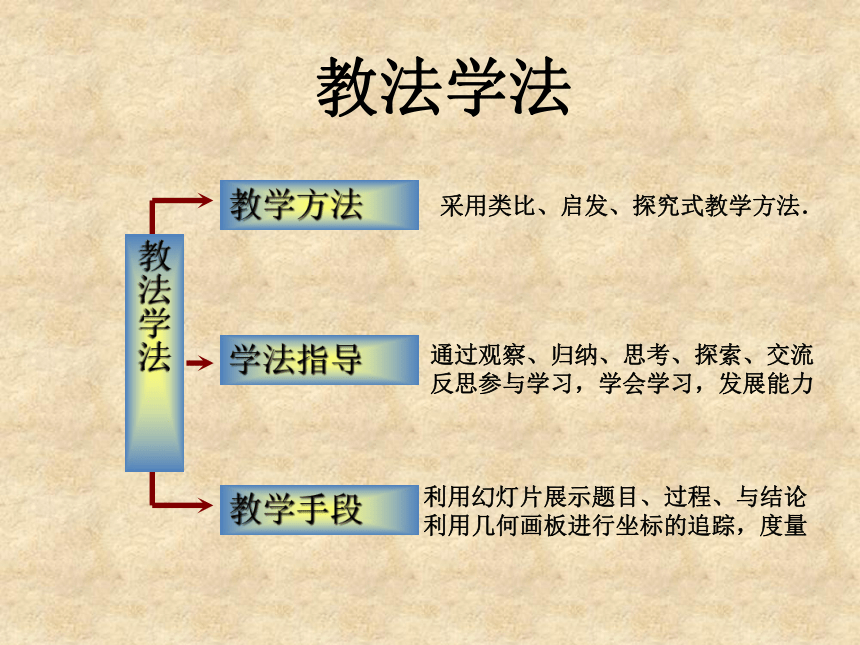
表示的平面区域。 教学重难点 利用幻灯片展示题目、过程、与结论
利用几何画板进行坐标的追踪,度量 采用类比、启发、探究式教学方法. 通过观察、归纳、思考、探索、交流反思参与学习,学会学习,发展能力教学方法学法指导教学手段教法学法教法学法
【例题1】一家银行的信贷部门计划年初投入2500万元用于企业和个人贷款,希望这笔资金至少可带来3万元的收益,其中从企业贷款中获益12%,从个人贷款中获益10%。那么,信贷部门应该如何分配资金呢?如果用于企业贷款和个人贷款的资金分别为x元,y元,你能用不等式刻画其中的不等量关系吗?
导入【1】把实际问题转化为数学问题:用于企业贷款的资金为x万元,用于个人贷款的资金为y万元。
【2】把文字语言转化为符号语言:由资金总数为2500万元,得到 。由于预计贷款创收3万元以上,所以 ,即 。
最后考虑到用于企业和个人贷款的资金数额都不能是负值,于是
【3】抽象出数学模型
分配资金应满足条件: 解析 (1)二元一次不等式: 含有两个未知数,并且未知数的最高次数
是1的不等式; (2)二元一次不等式组:: 由几个二元一次不等式组成的不等式组; (3)二元一次不等式(组)的解集: 满足二元一次不等式(组)的有序实数对(x,y)构成的集合;可以看成是直角坐标系内的点构成的集合。 如:不等式组
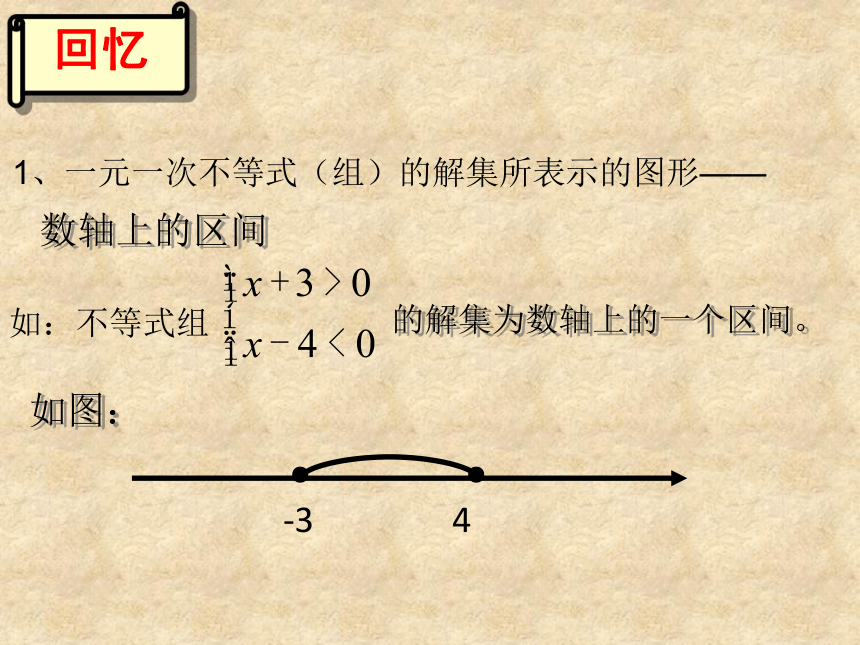
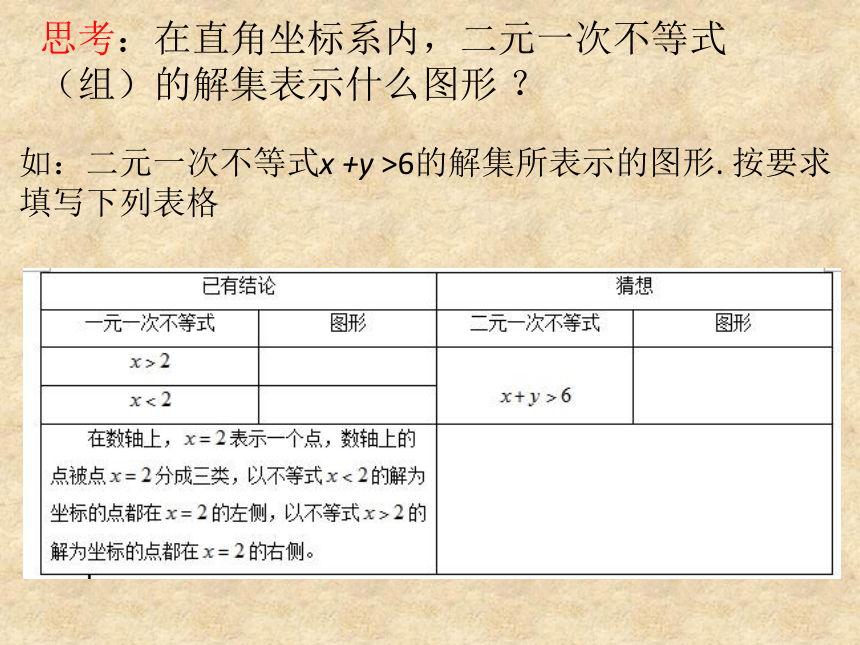
1、一元一次不等式(组)的解集所表示的图形——●●-34的解集为数轴上的一个区间。如图:数轴上的区间 回忆 思考:在直角坐标系内,二元一次不等式(组)的解集表示什么图形 ?如:二元一次不等式x +y >6的解集所表示的图形. 按要求填写下列表格 设点P(x,y 1)是直线x +y = 6上点,选取点A(x,y 2),使它的坐标满足不等式x + y > 6,请完成下面的表格探究 : 设点P(x,y 1)是直线x + y = 6
上的点,选取点A(x,y 2),使它的坐标满足不等式x +y > 6,请完成下面的表格探究 : 以不等式x + y > 6为坐标的点
都在直线x + y =6的右上方(区域) 结论一:结论二:直线x + y =6的右上方区域
的点满足不等式x + y >6 不等式x – y < 6表示直线
x – y =6左侧的平面区域; 不等式y—x <- 6表示直线
y—x =- 6右侧的平面区域; 练习 从特殊到一般情况: 二元一次不等式Ax + By + C>0(或<0)在平面直角坐标系中表示直线Ax + By + C = 0某一侧 所有点组成的平面区域(虚线表示区域不包括边界直线,实线包括边界直线)请同学们各抒己见。。。 法一:“移项变形” 法二:根据B取值与不等号方向的异同判断“上同下异”原则例1:画出不等式 x + 4y < 4表示的平面区域 解:B=4>0,不等号为小于0,由“上同下异”原则,
取直线下方。例1:画出不等式 x + 4y < 4表示的平面区域 画直线x + 4y – 4 = 0(画成虚线)所以,不等式x + 4y – 4 < 0表示的区域
在直线x + 4y – 4 = 0的
左侧如图所示。(------直线定界)取原点(0,0),代入x + 4y - 4,
因为 0 + 4×0 – 4 = -4 < 0(-------特殊点定域) 法三:“直线定界,特殊点定域” 例2:画出不等式组
表示的平面区域x+y=0x=3x-y+5=0注:不等式组表示的平面区域是各不等式
所表示平面区域的公共部分。-55则用不等式可表示为:解:此平面区域在x-y=0的右侧, x-y≥0它又在x+2y-4=0的左侧, x+2y-4≤0它还在y+2=0的上方, y+2≥0求由三直线x-y=0;x+2y-4=0及y+2=0
所围成的平面区域所表示的不等式。思考:课堂小结:请同学们谈一谈本节课的收获,可从知识与思想方面谈。知识:
二元一次不等式(组)表示平面区域的方法:
法一,“移项变形”;
法二,看B,“上同下异”;
法三,“直线定界,特殊点定域”。
思想:数形结合的方法与分类讨论思想;猜想、证明、对比归纳的研究方法。4-2332 课堂作业:.画出下列不等式组表示的平面区域2y=-2y=xx+2y=43x+2y=6x-3y+9=0x-2y=0X=3(1)(2)
2、经历自主探究分析问题和解决问题的能力;理解数学的转化,数形结合以及分类讨论思想;
3、通过主动参与合作交流,培养团队协作和勇于探索的精神;体会数学的应用价值;体会由特殊到一般的思想。教学重点:
探究特殊二元一次不等式的平面区域。
教学难点:
探究一般二元一次不等式
表示的平面区域。 教学重难点 利用幻灯片展示题目、过程、与结论
利用几何画板进行坐标的追踪,度量 采用类比、启发、探究式教学方法. 通过观察、归纳、思考、探索、交流反思参与学习,学会学习,发展能力教学方法学法指导教学手段教法学法教法学法
【例题1】一家银行的信贷部门计划年初投入2500万元用于企业和个人贷款,希望这笔资金至少可带来3万元的收益,其中从企业贷款中获益12%,从个人贷款中获益10%。那么,信贷部门应该如何分配资金呢?如果用于企业贷款和个人贷款的资金分别为x元,y元,你能用不等式刻画其中的不等量关系吗?
导入【1】把实际问题转化为数学问题:用于企业贷款的资金为x万元,用于个人贷款的资金为y万元。
【2】把文字语言转化为符号语言:由资金总数为2500万元,得到 。由于预计贷款创收3万元以上,所以 ,即 。
最后考虑到用于企业和个人贷款的资金数额都不能是负值,于是
【3】抽象出数学模型
分配资金应满足条件: 解析 (1)二元一次不等式: 含有两个未知数,并且未知数的最高次数
是1的不等式; (2)二元一次不等式组:: 由几个二元一次不等式组成的不等式组; (3)二元一次不等式(组)的解集: 满足二元一次不等式(组)的有序实数对(x,y)构成的集合;可以看成是直角坐标系内的点构成的集合。 如:不等式组
1、一元一次不等式(组)的解集所表示的图形——●●-34的解集为数轴上的一个区间。如图:数轴上的区间 回忆 思考:在直角坐标系内,二元一次不等式(组)的解集表示什么图形 ?如:二元一次不等式x +y >6的解集所表示的图形. 按要求填写下列表格 设点P(x,y 1)是直线x +y = 6上点,选取点A(x,y 2),使它的坐标满足不等式x + y > 6,请完成下面的表格探究 : 设点P(x,y 1)是直线x + y = 6
上的点,选取点A(x,y 2),使它的坐标满足不等式x +y > 6,请完成下面的表格探究 : 以不等式x + y > 6为坐标的点
都在直线x + y =6的右上方(区域) 结论一:结论二:直线x + y =6的右上方区域
的点满足不等式x + y >6 不等式x – y < 6表示直线
x – y =6左侧的平面区域; 不等式y—x <- 6表示直线
y—x =- 6右侧的平面区域; 练习 从特殊到一般情况: 二元一次不等式Ax + By + C>0(或<0)在平面直角坐标系中表示直线Ax + By + C = 0某一侧 所有点组成的平面区域(虚线表示区域不包括边界直线,实线包括边界直线)请同学们各抒己见。。。 法一:“移项变形” 法二:根据B取值与不等号方向的异同判断“上同下异”原则例1:画出不等式 x + 4y < 4表示的平面区域 解:B=4>0,不等号为小于0,由“上同下异”原则,
取直线下方。例1:画出不等式 x + 4y < 4表示的平面区域 画直线x + 4y – 4 = 0(画成虚线)所以,不等式x + 4y – 4 < 0表示的区域
在直线x + 4y – 4 = 0的
左侧如图所示。(------直线定界)取原点(0,0),代入x + 4y - 4,
因为 0 + 4×0 – 4 = -4 < 0(-------特殊点定域) 法三:“直线定界,特殊点定域” 例2:画出不等式组
表示的平面区域x+y=0x=3x-y+5=0注:不等式组表示的平面区域是各不等式
所表示平面区域的公共部分。-55则用不等式可表示为:解:此平面区域在x-y=0的右侧, x-y≥0它又在x+2y-4=0的左侧, x+2y-4≤0它还在y+2=0的上方, y+2≥0求由三直线x-y=0;x+2y-4=0及y+2=0
所围成的平面区域所表示的不等式。思考:课堂小结:请同学们谈一谈本节课的收获,可从知识与思想方面谈。知识:
二元一次不等式(组)表示平面区域的方法:
法一,“移项变形”;
法二,看B,“上同下异”;
法三,“直线定界,特殊点定域”。
思想:数形结合的方法与分类讨论思想;猜想、证明、对比归纳的研究方法。4-2332 课堂作业:.画出下列不等式组表示的平面区域2y=-2y=xx+2y=43x+2y=6x-3y+9=0x-2y=0X=3(1)(2)
