人教A版数学必修4 1.3 三角函数的诱导公式(共17张ppt)
文档属性
| 名称 | 人教A版数学必修4 1.3 三角函数的诱导公式(共17张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 763.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-17 00:00:00 | ||
图片预览



文档简介
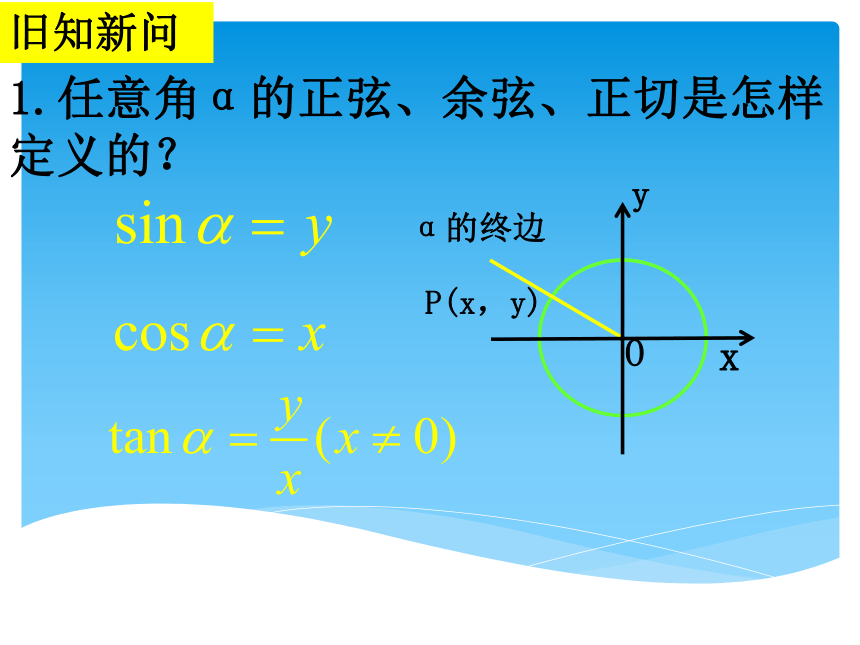
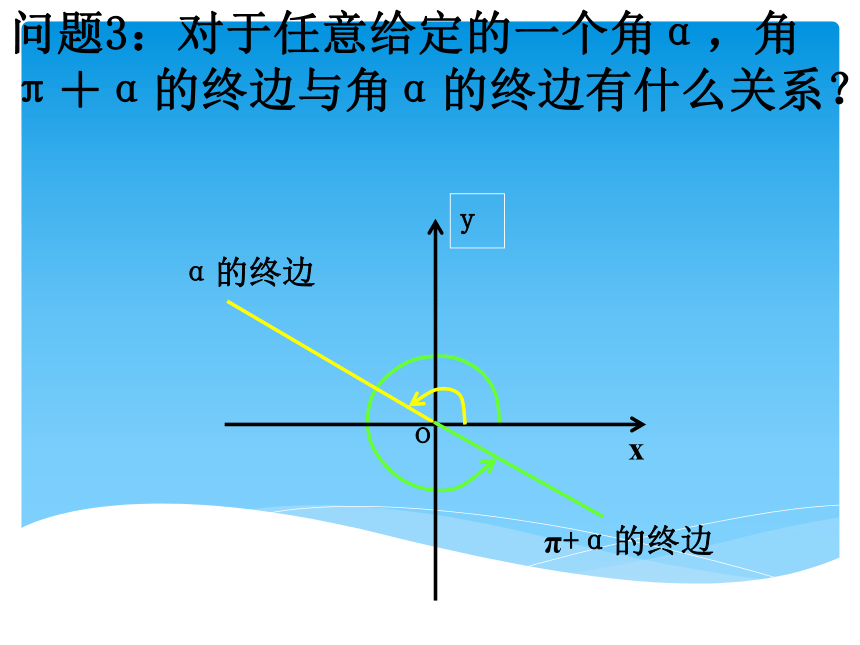
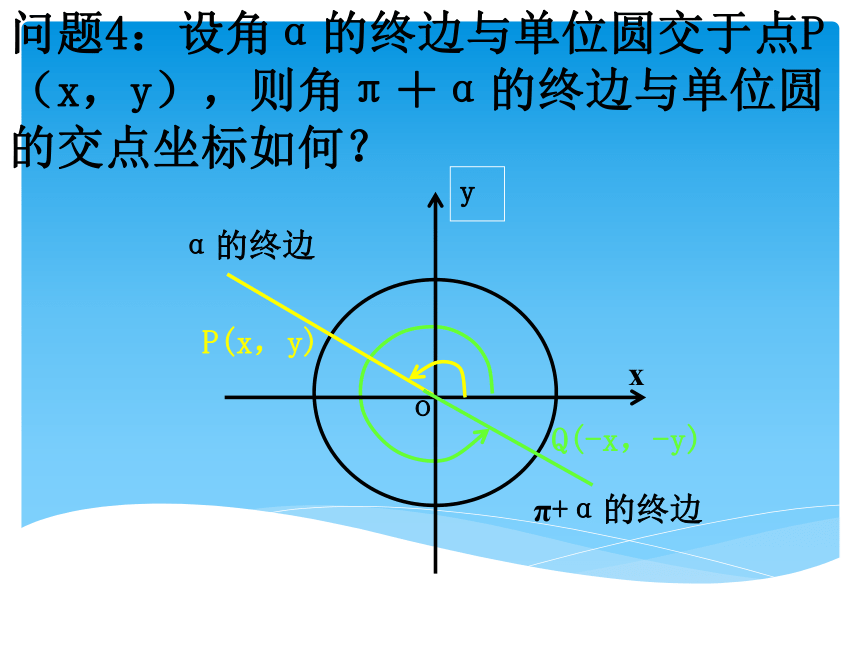
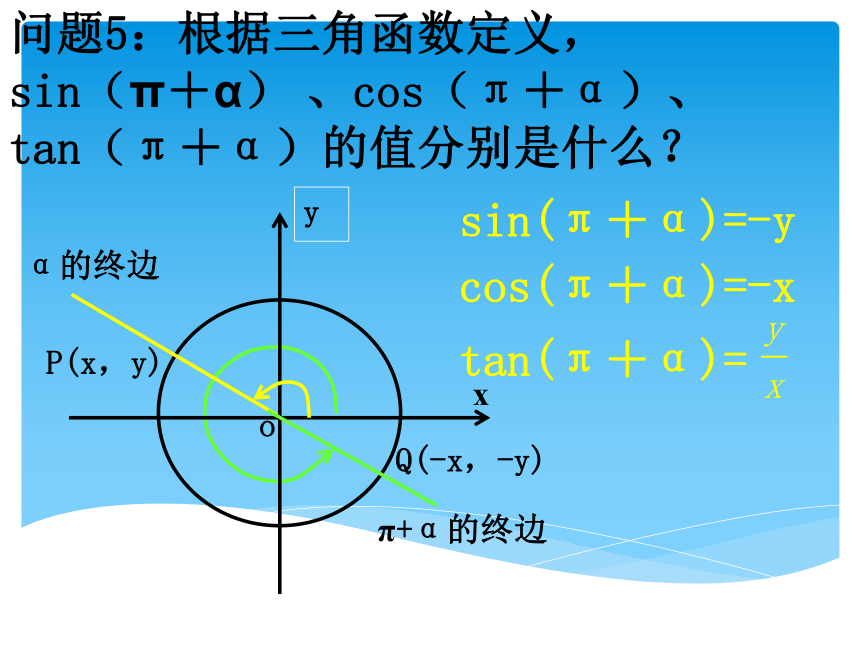
课件17张PPT。三角函数的诱导公式旧知新问1.任意角α的正弦、余弦、正切是怎样定义的?2. 2kπ+α(k∈Z)与α的三角函数之间的关系是什么?3.你能求sin750°和sin930°的值吗?知识探究(一):π+α的诱导公式 问题1:210°角与30°角有何内在联系?问题2:(180°,270°)范围内的角可以怎样表示?210°=180°+30°若α为锐角,则角可表示180°+α问题3:对于任意给定的一个角α,角π+α的终边与角α的终边有什么关系?问题4:设角α的终边与单位圆交于点P(x,y),则角π+α的终边与单位圆的交点坐标如何?Q(-x,-y)问题5:根据三角函数定义,
sin(π+α) 、cos(π+α)、
tan(π+α)的值分别是什么?sin(π+α)=-ycos(π+α)=-xtan(π+α)=问题6:对比sinα,cosα,tanα的值,π+α的三角函数与α的三角函数有什么关系? 公式二: 知识探究(二):-α,π-α的诱导公式: 问题2:设角α的终边与单位圆交于点 P(x,y),则-α的终边与单位圆的交点坐标如何?P(x,-y) 公式三: 问题3:根据三角函数定义,-α的三角函数与α的三角函数有什么关系?问题4:如何根据三角函数定义推导公式四?P(x,y)P(-x,y) 公式四: 公式一:公式二:公式三:公式四:诱导公式简记为“函数名不变,符号看象限” 的三角函数值,等于 的同名三角函数值前面加上把 看作锐角时原函数值的符号。发现规律:公式一、二、三、四,都叫做诱导公式.理论迁移例1 求下列各三角函数的值:例3 化简
.1.诱导公式都是恒等式,即在等式有意义时恒成立.小结2、利用诱导公式一~四,可以求任意角的三角函数,化为锐角三角函数其基本思路是:负化正,大化小,化到锐角为终了。
sin(π+α) 、cos(π+α)、
tan(π+α)的值分别是什么?sin(π+α)=-ycos(π+α)=-xtan(π+α)=问题6:对比sinα,cosα,tanα的值,π+α的三角函数与α的三角函数有什么关系? 公式二: 知识探究(二):-α,π-α的诱导公式: 问题2:设角α的终边与单位圆交于点 P(x,y),则-α的终边与单位圆的交点坐标如何?P(x,-y) 公式三: 问题3:根据三角函数定义,-α的三角函数与α的三角函数有什么关系?问题4:如何根据三角函数定义推导公式四?P(x,y)P(-x,y) 公式四: 公式一:公式二:公式三:公式四:诱导公式简记为“函数名不变,符号看象限” 的三角函数值,等于 的同名三角函数值前面加上把 看作锐角时原函数值的符号。发现规律:公式一、二、三、四,都叫做诱导公式.理论迁移例1 求下列各三角函数的值:例3 化简
.1.诱导公式都是恒等式,即在等式有意义时恒成立.小结2、利用诱导公式一~四,可以求任意角的三角函数,化为锐角三角函数其基本思路是:负化正,大化小,化到锐角为终了。
