人教A版数学必修4 2.5.1 平面向量的几何应用(共16张ppt)
文档属性
| 名称 | 人教A版数学必修4 2.5.1 平面向量的几何应用(共16张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 204.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-17 00:00:00 | ||
图片预览





文档简介
课件16张PPT。2.5.1平面几何中的向量方法人民教育出版社数学必修四回顾双基 温故知新
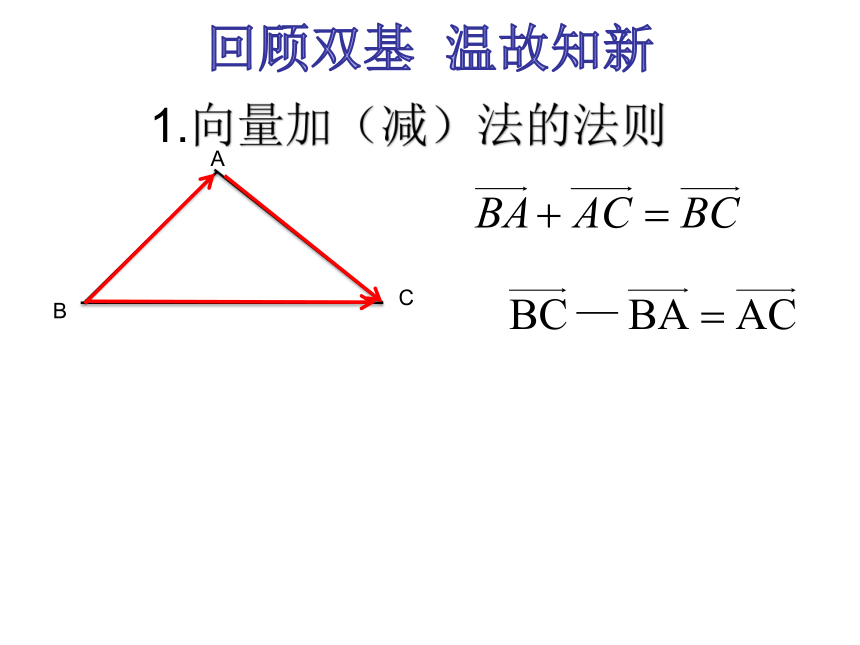
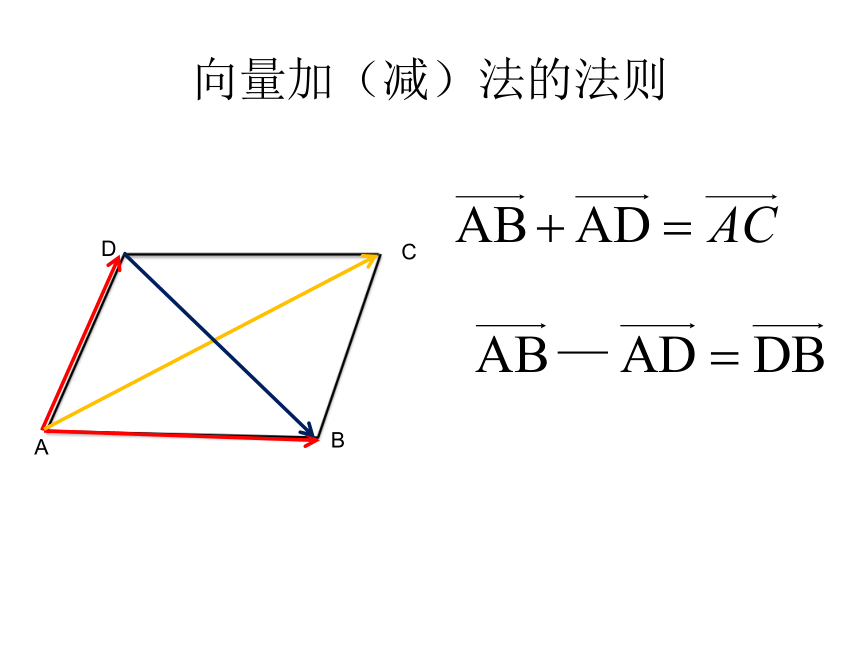
1.向量加(减)法的法则向量加(减)法的法则2.回顾双基 温故知新3.平面向量的基本定理学生探索 尝试解决平面几何中的向量方法 欧氏几何的论证严谨优雅,给人以极大的美感和享受,但有较大的思考难度,对人的智力形成极大的挑战。而1967年笛卡尔的《方法谈》及其附录《几何法》发表,引入了坐标,解析几何学建立,为数学提供了一种新工具;18世纪末,挪威测量学家维塞尔把坐标平面上的点用向量表示,并把向量的几何表示用于研究几何问题,为我们找到了一个更便捷的工具。 例1.平行四边形是表示向量加法与减法的几何模型。 如图,你能发现平行四边形对角线的长度与两条邻边长度之间的关系吗?思考:长方形对角线的长度与两条邻边长度之间有何关系?猜想:平行四边形相似关系?设计问题 深化提高例1、已知:平行四边形ABCD。
求证:解:设 ,则
分析:因为平行四边形对边平行且相
等,故设 其它线段对应向
量用它们表示。
即平行四边形两条对角线的平方和等于两条邻边平方和的两倍。信息交流 揭示规律(1)建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题;
(2)通过向量运算,研究几何元素之间的关系,如距离、夹角等问题;
(3)把运算结果“翻译”成几何元素。用向量方法解决平面几何问题的“三部曲”:例2 如图,平行四边形ABCD中,点E、F分别是AD 、 DC边的中点,BE 、 BF分别与AC交于R 、 T两点,你能发现AR 、 RT 、TC之间的关系吗?猜想:
AR=RT=TCAR=RT=TC即R,T为AC的三等分点,我们只要证出 向量AR还可以怎么构造呢?解:线,故AT=RT=TC练习分析:(1)建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题;
(2)通过向量运算,研究几何元素之间的关系,如距离、夹角等问题;
(3)把运算结果“翻译”成几何元素。(1)用向量方法解决平面几何问题的“三步曲”:反思小结 观点提炼(2)本节课所用到的数学方法,数学思想有哪些?数学思想:方程的思想,数形结合的思想,转化和化归的思想数学方法:待定系数法
1.向量加(减)法的法则向量加(减)法的法则2.回顾双基 温故知新3.平面向量的基本定理学生探索 尝试解决平面几何中的向量方法 欧氏几何的论证严谨优雅,给人以极大的美感和享受,但有较大的思考难度,对人的智力形成极大的挑战。而1967年笛卡尔的《方法谈》及其附录《几何法》发表,引入了坐标,解析几何学建立,为数学提供了一种新工具;18世纪末,挪威测量学家维塞尔把坐标平面上的点用向量表示,并把向量的几何表示用于研究几何问题,为我们找到了一个更便捷的工具。 例1.平行四边形是表示向量加法与减法的几何模型。 如图,你能发现平行四边形对角线的长度与两条邻边长度之间的关系吗?思考:长方形对角线的长度与两条邻边长度之间有何关系?猜想:平行四边形相似关系?设计问题 深化提高例1、已知:平行四边形ABCD。
求证:解:设 ,则
分析:因为平行四边形对边平行且相
等,故设 其它线段对应向
量用它们表示。
即平行四边形两条对角线的平方和等于两条邻边平方和的两倍。信息交流 揭示规律(1)建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题;
(2)通过向量运算,研究几何元素之间的关系,如距离、夹角等问题;
(3)把运算结果“翻译”成几何元素。用向量方法解决平面几何问题的“三部曲”:例2 如图,平行四边形ABCD中,点E、F分别是AD 、 DC边的中点,BE 、 BF分别与AC交于R 、 T两点,你能发现AR 、 RT 、TC之间的关系吗?猜想:
AR=RT=TCAR=RT=TC即R,T为AC的三等分点,我们只要证出 向量AR还可以怎么构造呢?解:线,故AT=RT=TC练习分析:(1)建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题;
(2)通过向量运算,研究几何元素之间的关系,如距离、夹角等问题;
(3)把运算结果“翻译”成几何元素。(1)用向量方法解决平面几何问题的“三步曲”:反思小结 观点提炼(2)本节课所用到的数学方法,数学思想有哪些?数学思想:方程的思想,数形结合的思想,转化和化归的思想数学方法:待定系数法
