人教A版数学必修4 1.6 三角函数模型的简单应用(共17张ppt)
文档属性
| 名称 | 人教A版数学必修4 1.6 三角函数模型的简单应用(共17张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-17 09:07:21 | ||
图片预览




文档简介
课件17张PPT。三角函数模型的简单应用4必 修A人民教育出版社版数学复习回顾A函数模型的应用示例正弦函数y=sinx
余弦函数y=cosx
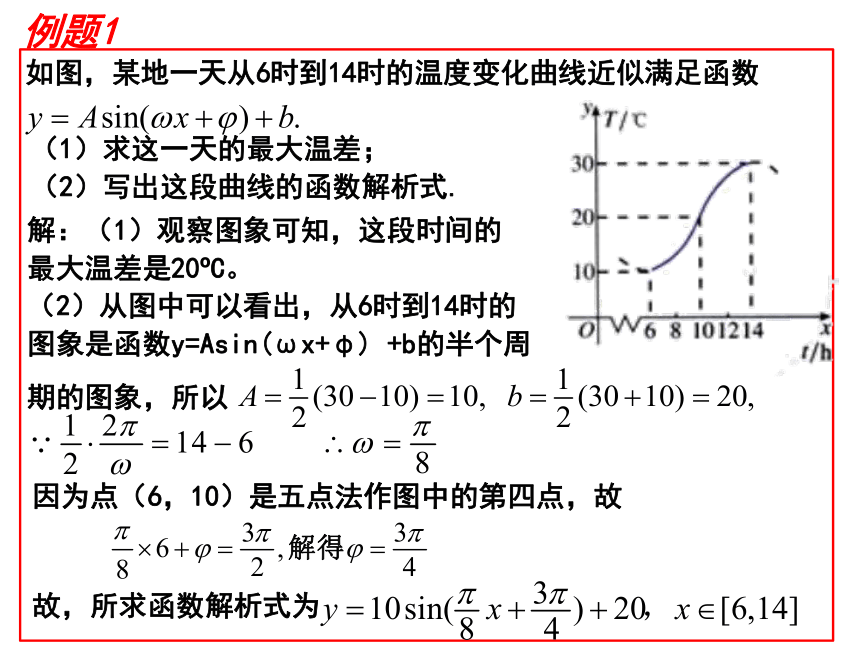
如图,某地一天从6时到14时的温度变化曲线近似满足函数(1)求这一天的最大温差;
(2)写出这段曲线的函数解析式.解:(1)观察图象可知,这段时间的
最大温差是20oC。
(2)从图中可以看出,从6时到14时的
图象是函数y=Asin(ωx+φ) +b的半个周
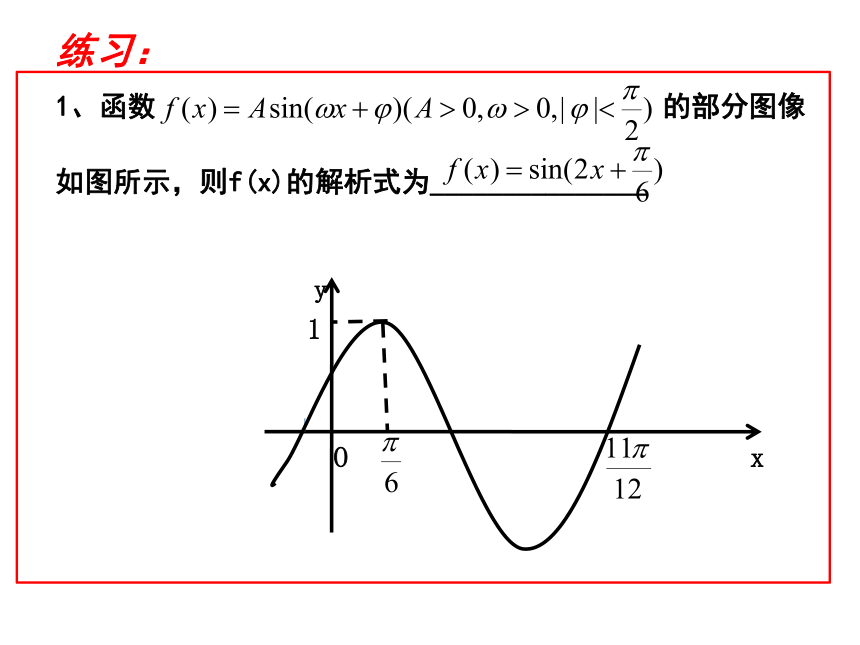
期的图象,所以因为点(6,10)是五点法作图中的第四点,故例题1Oyx1练习:1、函数 的部分图像
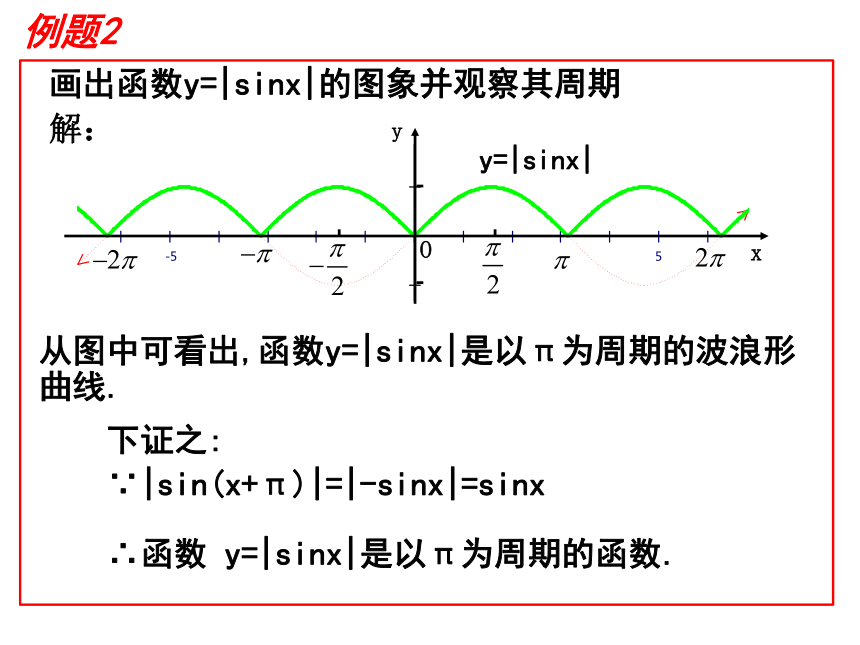
如图所示,则f(x)的解析式为_______________画出函数y=|sinx|的图象并观察其周期从图中可看出,函数y=|sinx|是以π为周期的波浪形曲线.解:y=|sinx|例题2练习2:画出下列函数的图像(1)(2) 如图所示,大风车的半径为2m,每12s旋转一周,它
的最低点O离地面0.5m.风车圆周上一点A从最低点O开
始,运动t(s)后与地面的距离为h m. (1)求函数h=f(t)的关系式. (2)画出函数h=f(t)的图象.
例题3h将实际问题抽象为三角函数模型的一般步聚:小结:1.三角函数作为描述现实世界中周期现象的一种数学模型,可以用来研究很多问题,我们可以通过建立三角函数模型来解决实际问题,如天气预报,地震预测,等等.2.建立三角函数模型的一般步聚:yxOAByxOyxOyxOCD1、函数y=-xcosx的部分图像是( )2、函数 的部分图像如图所示,
则该函数的表达式为( )巩固练习DC三角函数离我们有多近?1、你能一刀削出一条正弦曲线吗? 提示:把一张纸卷到圆柱形的纸筒面上,卷上几圈,用刀斜着将纸筒削断,再把卷着的纸展开,你就会看到:纸的边缘线是一条波浪形的曲线。你知道吗?
这条曲线就是正弦曲线!2、你能试着针对周围一些呈周期性变化的现象编拟一道能用三角函数模型解决它的题吗?
余弦函数y=cosx
如图,某地一天从6时到14时的温度变化曲线近似满足函数(1)求这一天的最大温差;
(2)写出这段曲线的函数解析式.解:(1)观察图象可知,这段时间的
最大温差是20oC。
(2)从图中可以看出,从6时到14时的
图象是函数y=Asin(ωx+φ) +b的半个周
期的图象,所以因为点(6,10)是五点法作图中的第四点,故例题1Oyx1练习:1、函数 的部分图像
如图所示,则f(x)的解析式为_______________画出函数y=|sinx|的图象并观察其周期从图中可看出,函数y=|sinx|是以π为周期的波浪形曲线.解:y=|sinx|例题2练习2:画出下列函数的图像(1)(2) 如图所示,大风车的半径为2m,每12s旋转一周,它
的最低点O离地面0.5m.风车圆周上一点A从最低点O开
始,运动t(s)后与地面的距离为h m. (1)求函数h=f(t)的关系式. (2)画出函数h=f(t)的图象.
例题3h将实际问题抽象为三角函数模型的一般步聚:小结:1.三角函数作为描述现实世界中周期现象的一种数学模型,可以用来研究很多问题,我们可以通过建立三角函数模型来解决实际问题,如天气预报,地震预测,等等.2.建立三角函数模型的一般步聚:yxOAByxOyxOyxOCD1、函数y=-xcosx的部分图像是( )2、函数 的部分图像如图所示,
则该函数的表达式为( )巩固练习DC三角函数离我们有多近?1、你能一刀削出一条正弦曲线吗? 提示:把一张纸卷到圆柱形的纸筒面上,卷上几圈,用刀斜着将纸筒削断,再把卷着的纸展开,你就会看到:纸的边缘线是一条波浪形的曲线。你知道吗?
这条曲线就是正弦曲线!2、你能试着针对周围一些呈周期性变化的现象编拟一道能用三角函数模型解决它的题吗?
