人教A版数学选修2—1 1.4 全称量词和存在量词(共24张ppt)
文档属性
| 名称 | 人教A版数学选修2—1 1.4 全称量词和存在量词(共24张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 385.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-17 00:00:00 | ||
图片预览







文档简介
课件24张PPT。1.4 全称量词与存在量词1.理解全称量词、存在量词和全称命题、特称命题的概念.
2.能准确地使用全称量词和存在量词的符号(即?,?)来表述相关的数学内容.
3.掌握判断全称命题和特称命题的真假的基本原则和方法.
教学目标 德国数学家哥德巴赫在1742年6月7日给欧拉的信中提出了以下猜想:
(a)任何一个不小于6的偶数,都可以表示成两个奇质数之和;
(b) 任何一个不小于9的奇数,都可以表示成三个奇质数之和。
这就是著名的哥德巴赫猜想。请问:这两个猜想是命题吗?它们含有哪个量词?下列语句是命题吗?(1)与(3),(2)与(4)之间有什么关系?
(1)x>3;
(2) 2x+1是整数;
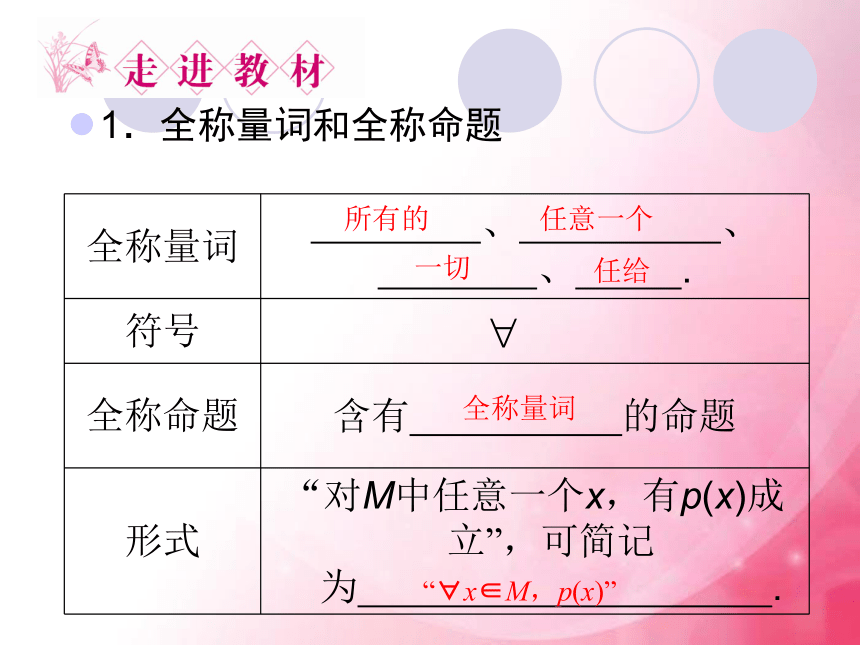
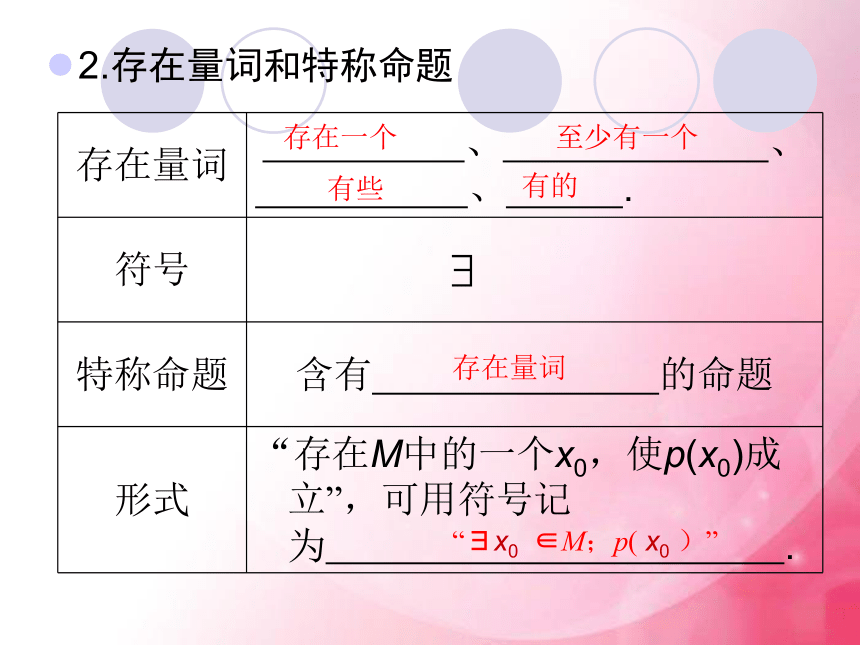
(3)对所有的X>3;(4)对任意一个,2x+1是整数。想一想??1.全称量词和全称命题所有的任意一个任给全称量词“?x∈M,p(x)”一切2.存在量词和特称命题存在一个至少有一个有的存在量词“?x0 ∈M;p( x0 )”有些 如何理解全称命题和特称命题?
全称命题是陈述某集合中的所有元素都具有(不具有)某种性质的命题,强调“整体、全部”.
特称命题是陈述某集合中有存在一个元素具有(不具有)某种性质的命题,强调“个别、部分”的特殊性.①所有的x∈A,p(x)成立
②对一切x∈A,p(x)成立
③对每一个x∈A,p(x)成立
④任选一个x∈A,使p(x)成立
⑤凡x∈A,都有p(x)成立①存在x∈A,使p(x)成立
②至少有一个x∈A,使p(x)成立
③对有些x∈A,使p(x)成立
④对某个x∈A,使p(x)成立
⑤有一个x∈A,使p(x)成立.请小组讨论所学的命题中是否出现过全程量词和存在量词?若有,请举例说明。上述定义、定理中出现的全称量词与存在量词可以互换或删除吗?3. 将下列命题用量词符号“?”或“?”表示,并判断真假.
(1)实数的平方是非负数;
(2)整数中1最小;
(3)方程ax2+2x+1=0(a<1)至少存在一个负根;
(4)对于某些实数x,有2x+1>0;
(5)若直线l垂直于平面α内任一直线,则l⊥α.[解题过程] 例2 判断下列特称命题的真假:
1)有一个实数 ,使 2)存在两个相交平面垂直于同一条直线;
3)有些整数只有两个正因数。1.将“x2+y2≥2xy”改写成全称命题,下列说法正确的是( )
A.?x,y∈R,都有x2+y2≥2xy
B.?x0,y0∈R,使x+y≥2x0y0
C.?x>0,y>0,都有x2+y2≥2xy
D.?x0<0,y0<0,使x+y≤2x0y0
2.指出下列命题中,哪些是全称命题,哪些是特称命题,并判断真假:
(1)当a>1时,则对任意x,曲线y=ax与曲线y=logax有交点.
(2)?x∈R,使得x2-x+1≤0.
(3)被5整除的整数的末位数字都是0.
(4)有的四边形没有外接圆.[题后感悟] 判定一个语句是全称命题还是特称命题可分三个步骤:
(1)首先判定语句是否为命题,若不是命题,就当然不是全称命题或特称命题.
(2)若是命题,再分析命题中所含的量词,含有全称量词的命题是全称命题,含有存在量词的命题是特称命题.
(3)当命题中不含量词时,要注意理解命题含义的实质.已知函数f(x)=x2-2x+5.
(1)是否存在实数m,使不等式m+f(x)>0对于任意 x∈R恒成立,并说明理由.
(2)若存在一个实数x0,使不等式m-f(x0)>0成立,求实数m的取值范围. 拓展升华解:(1)不等式m+f(x)>0可化为m>-f(x),
即m>-x2+2x-5=-(x-1)2-4.
要使m>-(x-1)2-4对于任意x∈R恒成立,只需m>-4即可.
故存在实数m,使不等式m+f(x)>0对于任意x∈R恒成立,此时,只需m>-4.(2)不等式m-f(x0)>0可化为m>f(x0),若存在一个实数x0,使不等式m>f(x0)成立,只需m>f(x)min.
又f(x)=(x-1)2+4,∴f(x)min=4,∴m>4.
所以,所求实数m的取值范围是(4,+∞).知识小结
2.能准确地使用全称量词和存在量词的符号(即?,?)来表述相关的数学内容.
3.掌握判断全称命题和特称命题的真假的基本原则和方法.
教学目标 德国数学家哥德巴赫在1742年6月7日给欧拉的信中提出了以下猜想:
(a)任何一个不小于6的偶数,都可以表示成两个奇质数之和;
(b) 任何一个不小于9的奇数,都可以表示成三个奇质数之和。
这就是著名的哥德巴赫猜想。请问:这两个猜想是命题吗?它们含有哪个量词?下列语句是命题吗?(1)与(3),(2)与(4)之间有什么关系?
(1)x>3;
(2) 2x+1是整数;
(3)对所有的X>3;(4)对任意一个,2x+1是整数。想一想??1.全称量词和全称命题所有的任意一个任给全称量词“?x∈M,p(x)”一切2.存在量词和特称命题存在一个至少有一个有的存在量词“?x0 ∈M;p( x0 )”有些 如何理解全称命题和特称命题?
全称命题是陈述某集合中的所有元素都具有(不具有)某种性质的命题,强调“整体、全部”.
特称命题是陈述某集合中有存在一个元素具有(不具有)某种性质的命题,强调“个别、部分”的特殊性.①所有的x∈A,p(x)成立
②对一切x∈A,p(x)成立
③对每一个x∈A,p(x)成立
④任选一个x∈A,使p(x)成立
⑤凡x∈A,都有p(x)成立①存在x∈A,使p(x)成立
②至少有一个x∈A,使p(x)成立
③对有些x∈A,使p(x)成立
④对某个x∈A,使p(x)成立
⑤有一个x∈A,使p(x)成立.请小组讨论所学的命题中是否出现过全程量词和存在量词?若有,请举例说明。上述定义、定理中出现的全称量词与存在量词可以互换或删除吗?3. 将下列命题用量词符号“?”或“?”表示,并判断真假.
(1)实数的平方是非负数;
(2)整数中1最小;
(3)方程ax2+2x+1=0(a<1)至少存在一个负根;
(4)对于某些实数x,有2x+1>0;
(5)若直线l垂直于平面α内任一直线,则l⊥α.[解题过程] 例2 判断下列特称命题的真假:
1)有一个实数 ,使 2)存在两个相交平面垂直于同一条直线;
3)有些整数只有两个正因数。1.将“x2+y2≥2xy”改写成全称命题,下列说法正确的是( )
A.?x,y∈R,都有x2+y2≥2xy
B.?x0,y0∈R,使x+y≥2x0y0
C.?x>0,y>0,都有x2+y2≥2xy
D.?x0<0,y0<0,使x+y≤2x0y0
2.指出下列命题中,哪些是全称命题,哪些是特称命题,并判断真假:
(1)当a>1时,则对任意x,曲线y=ax与曲线y=logax有交点.
(2)?x∈R,使得x2-x+1≤0.
(3)被5整除的整数的末位数字都是0.
(4)有的四边形没有外接圆.[题后感悟] 判定一个语句是全称命题还是特称命题可分三个步骤:
(1)首先判定语句是否为命题,若不是命题,就当然不是全称命题或特称命题.
(2)若是命题,再分析命题中所含的量词,含有全称量词的命题是全称命题,含有存在量词的命题是特称命题.
(3)当命题中不含量词时,要注意理解命题含义的实质.已知函数f(x)=x2-2x+5.
(1)是否存在实数m,使不等式m+f(x)>0对于任意 x∈R恒成立,并说明理由.
(2)若存在一个实数x0,使不等式m-f(x0)>0成立,求实数m的取值范围. 拓展升华解:(1)不等式m+f(x)>0可化为m>-f(x),
即m>-x2+2x-5=-(x-1)2-4.
要使m>-(x-1)2-4对于任意x∈R恒成立,只需m>-4即可.
故存在实数m,使不等式m+f(x)>0对于任意x∈R恒成立,此时,只需m>-4.(2)不等式m-f(x0)>0可化为m>f(x0),若存在一个实数x0,使不等式m>f(x0)成立,只需m>f(x)min.
又f(x)=(x-1)2+4,∴f(x)min=4,∴m>4.
所以,所求实数m的取值范围是(4,+∞).知识小结
