江苏省苏州市2013-2019届高三上学期9月期初考试数学试题分类汇编:实际应用
文档属性
| 名称 | 江苏省苏州市2013-2019届高三上学期9月期初考试数学试题分类汇编:实际应用 |
|
|
| 格式 | zip | ||
| 文件大小 | 232.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-17 00:00:00 | ||
图片预览




文档简介
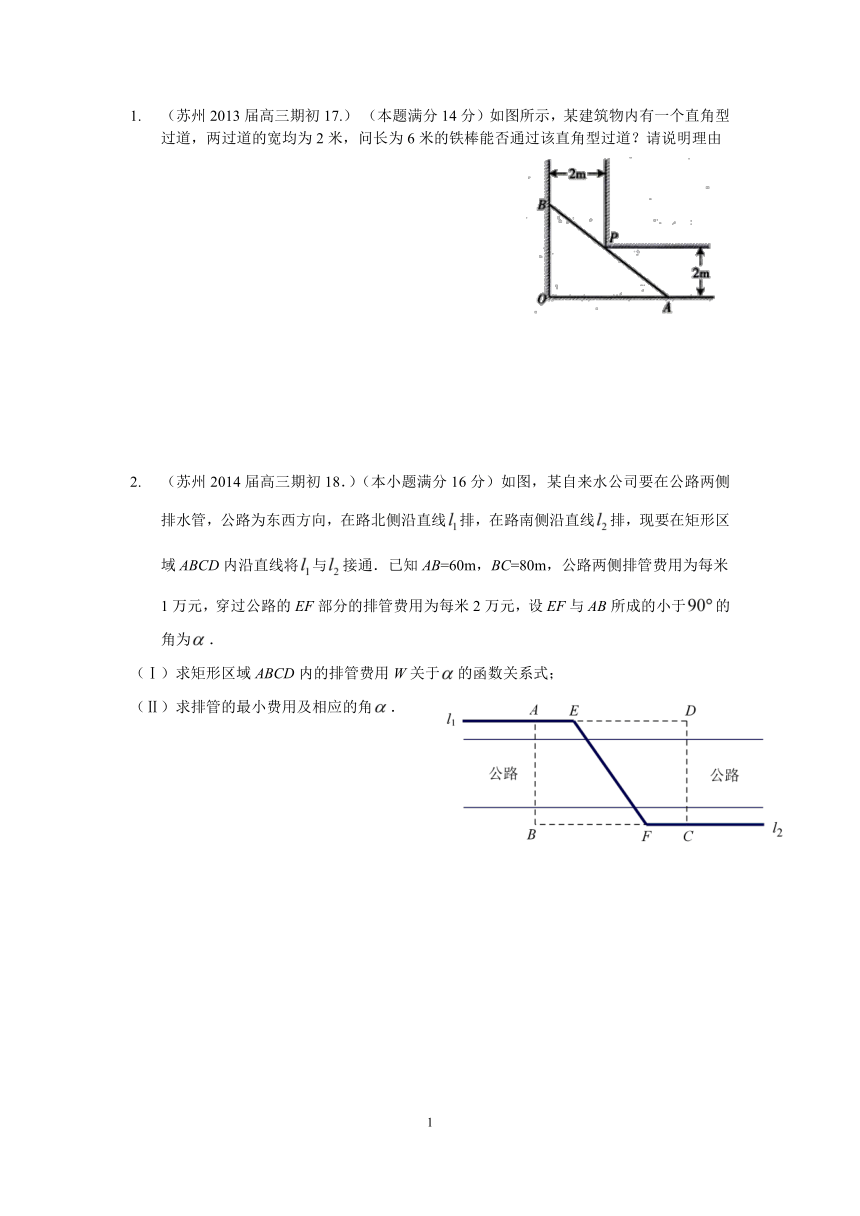
(苏州2013届高三期初17.) (本题满分14分)如图所示,某建筑物内有一个直角型过道,两过道的宽均为2米,问长为6米的铁棒能否通过该直角型过道?请说明理由
/
(苏州2014届高三期初18.)(本小题满分16分)如图,某自来水公司要在公路两侧排水管,公路为东西方向,在路北侧沿直线/排,在路南侧沿直线/排,现要在矩形区域ABCD内沿直线将/与/接通.已知AB=60m,BC=80m,公路两侧排管费用为每米1万元,穿过公路的EF部分的排管费用为每米2万元,设EF与AB所成的小于/的角为/.
(Ⅰ)求矩形区域ABCD内的排管费用W关于/的函数关系式;
(Ⅱ)求排管的最小费用及相应的角/.
(苏州2015届高三期初)18.(本小题满分16分)如图,有两条相交成60°角的直路XX(,YY(,交点是O,甲、乙分别在OX,OY上,起初甲离O点3,乙离O点1.后来甲沿XX(的方向,乙沿Y(Y的方向,同时用4的速度步行.
(1)起初两人的距离是多少?
(2)t 后两人的距离是多少?
(3)什么时候两人的距离最短?
(苏州2016届高三期初19. )如图,相距 14km 的两个居民小区 M 和 N 位于河岸 (直线)的同侧,M 和 N 到河岸的距离分别为 10km 和 8km.现要在河的小区一侧选一地点 P,在 P 处建一个生活污水处理站,并从 P 分别排设到两个小区的直线水管 PM,PN 和垂直于河岸的水管 PQ,使小区污水经处理后排入河道.设PQ 段水管长为 t km(0 < t < 8).
(1)求污水处理站 P 到两小区水管的长度之和的最小值(用 t 表示);
(2)试确定污水处理站 P 的位置,使所排三段水管的总长度最小,并分别求出此时污水处理站到两小区水管的长度.
(苏州2017届高三期初18.)(本小题满分16分)如图,某城市小区有一个矩形休闲广场,米,广场的一角是半径为米的扇形绿化区域,为了使小区居民能够更好的在广场休闲放松,现决定在广场上安置两排休闲椅,其中一排是穿越广场的双人靠背直排椅(宽度不计),点在线段上,并且与曲线相切;另一排为单人弧形椅沿曲线(宽度不计)摆放.已知双人靠背直排椅的造价每米为元,单人弧形椅的造价每米为元,记锐角,总造价为元.
(苏州2018届高三期初17.)(本小题满分14分)某公司设计如图所示的环状绿化景观带,该景观带的内圈由两条平行线段(图中的AB, DC )和两个半圆构成,设AB = x m,且x≥80.
(1)若内圈周长为400 m,则x取何值时,矩形ABCD的面积最大?
(2)若景观带的内圈所围成区域的面积为,则x取何值时,内圈周长最小?
(苏州2019届高三期初)17.(本题满分14分)如图,有一块半圆形的空地,政府计划在空地上建一个矩形的市民活动广场ABCD及矩形的停车场EFGH,剩余的地方进行绿化.其中半圆的圆心为O,半径为r,矩形的一边AB在直径上,点C,D,G,H在圆周上,E,F在边CD上,且∠BOG=,设.
(1)记市民活动广场及停车场的占地总面积为,求的表达式;
(2)当为何值时,可使市民活动广场及停车场的占地总面积最大.
答案:根据图得:l(θ)=BP+AP=+ ,θ∈(0, ),铁棒不能水平通过该直角过道,
理由如下:l′(θ)=( )′+( )′
= .
令l'(θ)=0得,θ= .
当0<θ< 时,l'(θ)<0,l(θ)为减函数;
当 <θ< 时,l'(θ)>0,l(θ)为增函数;
所以当θ= 时,l(θ)有最小值4 ,
因为4 <6,所以长为6米的铁棒不能水平通过该直角过道.
(苏州2014届高三期初18.)(本小题满分16分)如图,某自来水公司要在公路两侧排水管,公路为东西方向,在路北侧沿直线/排,在路南侧沿直线/排,现要在矩形区域ABCD内沿直线将/与/接通.已知AB=60m,BC=80m,公路两侧排管费用为每米1万元,穿过公路的EF部分的排管费用为每米2万元,设EF与AB所成的小于/的角为/.
(Ⅰ)求矩形区域ABCD内的排管费用W关于/的函数关系式;
(Ⅱ)求排管的最小费用及相应的角/.
(苏州2015届高三期初)18.(本小题满分16分)如图,有两条相交成60°角的直路XX(,YY(,交点是O,甲、乙分别在OX,OY上,起初甲离O点3,乙离O点1.后来甲沿XX(的方向,乙沿Y(Y的方向,同时用4的速度步行.
(1)起初两人的距离是多少?
(2)t 后两人的距离是多少?
(3)什么时候两人的距离最短?
18.解:(1)由余弦定理,得起初两人的距离为
. ··············4分
(2)设t 后两人的距离为d(t),则
当时,此时
··············8分
当时,此时
所以. ··············12分 (3)当()时,两人的距离最短. ············16分
解(I)如图,以河岸所在直线为 x 轴,
以过 M 垂直于的直线为 y 轴建立直角坐标系,
则可得点M (0, 10),点,
设点,
过作平行于 x 轴的直线,
作 关于 的对称点 ,
则,
所以
()即为所求。
(2设三段水管总长为 L,则 由( I )知
()
∴,
即方程在
上有解,故,,
解得,所以 L 的最小值为 21,此时对应的 (0, 8),
故,的方程为,令得,
即,从而,
答:满足题意的 P 点距河岸 5km,距小区 M 到河岸的垂线5 km,此时污水处理站到小区 M和 N 的水管长度分别为 10km 和 6km..
解:(1)过作的垂线,垂足为;过作的垂线,垂足为.
在中,,则
在中,,··············4分
由题意易得 ························6分
因此, ················7分
·············9分
(2)
令, ,因为,所以 ,······12分
设锐角满足,
当时,,单调递减;
当时,,单调递增.··················14分
所以当 ,总造价最小,最小值为,此时,,,因此当米时,能使总造价最小.··16分
(1)设半圆的半径为r, 可得2x+2πr=400,即x+πr=200, 矩形ABCD的面积为S=2xr=x?πr≤?()2=, 当且仅当x=πr=100m时,矩形的面积取得最大值m2; (2)设半圆的半径为r, 由题意可得πr2+2xr=,可得2x=-πr, 即有内圈周长c=2x+2πr=+πr, 由x≥80,可得-πr≥160, 解得0<πr≤90, 可得f(r)=+πr,f′(r)=π-, 即有f(r)在(0,]上递减, 即有πr=90,即x=80m时,周长c取得最小值340m.
17.(本题满分14分)
解:(1)∵半圆的半径为r,,∠OBC=90°.
∴在直角三角形OBC中,
,,∴.
∴. 2分
又∵∠BOG=,由半圆的对称性可知,∠HOA=,∴∠HOG=.
∴△HOG为等边三角形,∴HG=r,HE==.
∴. 4分
∴,其中.
7分
(2) ∵=. 9分
令,即,
解得:或(舍去). 11分
令,.
当时,,单调递增;
当时,,单调递减.
∴当时,取得最大值. 13分
答:当时,可使市民活动广场和停车场的面积总和最大. 14分
/
(苏州2014届高三期初18.)(本小题满分16分)如图,某自来水公司要在公路两侧排水管,公路为东西方向,在路北侧沿直线/排,在路南侧沿直线/排,现要在矩形区域ABCD内沿直线将/与/接通.已知AB=60m,BC=80m,公路两侧排管费用为每米1万元,穿过公路的EF部分的排管费用为每米2万元,设EF与AB所成的小于/的角为/.
(Ⅰ)求矩形区域ABCD内的排管费用W关于/的函数关系式;
(Ⅱ)求排管的最小费用及相应的角/.
(苏州2015届高三期初)18.(本小题满分16分)如图,有两条相交成60°角的直路XX(,YY(,交点是O,甲、乙分别在OX,OY上,起初甲离O点3,乙离O点1.后来甲沿XX(的方向,乙沿Y(Y的方向,同时用4的速度步行.
(1)起初两人的距离是多少?
(2)t 后两人的距离是多少?
(3)什么时候两人的距离最短?
(苏州2016届高三期初19. )如图,相距 14km 的两个居民小区 M 和 N 位于河岸 (直线)的同侧,M 和 N 到河岸的距离分别为 10km 和 8km.现要在河的小区一侧选一地点 P,在 P 处建一个生活污水处理站,并从 P 分别排设到两个小区的直线水管 PM,PN 和垂直于河岸的水管 PQ,使小区污水经处理后排入河道.设PQ 段水管长为 t km(0 < t < 8).
(1)求污水处理站 P 到两小区水管的长度之和的最小值(用 t 表示);
(2)试确定污水处理站 P 的位置,使所排三段水管的总长度最小,并分别求出此时污水处理站到两小区水管的长度.
(苏州2017届高三期初18.)(本小题满分16分)如图,某城市小区有一个矩形休闲广场,米,广场的一角是半径为米的扇形绿化区域,为了使小区居民能够更好的在广场休闲放松,现决定在广场上安置两排休闲椅,其中一排是穿越广场的双人靠背直排椅(宽度不计),点在线段上,并且与曲线相切;另一排为单人弧形椅沿曲线(宽度不计)摆放.已知双人靠背直排椅的造价每米为元,单人弧形椅的造价每米为元,记锐角,总造价为元.
(苏州2018届高三期初17.)(本小题满分14分)某公司设计如图所示的环状绿化景观带,该景观带的内圈由两条平行线段(图中的AB, DC )和两个半圆构成,设AB = x m,且x≥80.
(1)若内圈周长为400 m,则x取何值时,矩形ABCD的面积最大?
(2)若景观带的内圈所围成区域的面积为,则x取何值时,内圈周长最小?
(苏州2019届高三期初)17.(本题满分14分)如图,有一块半圆形的空地,政府计划在空地上建一个矩形的市民活动广场ABCD及矩形的停车场EFGH,剩余的地方进行绿化.其中半圆的圆心为O,半径为r,矩形的一边AB在直径上,点C,D,G,H在圆周上,E,F在边CD上,且∠BOG=,设.
(1)记市民活动广场及停车场的占地总面积为,求的表达式;
(2)当为何值时,可使市民活动广场及停车场的占地总面积最大.
答案:根据图得:l(θ)=BP+AP=+ ,θ∈(0, ),铁棒不能水平通过该直角过道,
理由如下:l′(θ)=( )′+( )′
= .
令l'(θ)=0得,θ= .
当0<θ< 时,l'(θ)<0,l(θ)为减函数;
当 <θ< 时,l'(θ)>0,l(θ)为增函数;
所以当θ= 时,l(θ)有最小值4 ,
因为4 <6,所以长为6米的铁棒不能水平通过该直角过道.
(苏州2014届高三期初18.)(本小题满分16分)如图,某自来水公司要在公路两侧排水管,公路为东西方向,在路北侧沿直线/排,在路南侧沿直线/排,现要在矩形区域ABCD内沿直线将/与/接通.已知AB=60m,BC=80m,公路两侧排管费用为每米1万元,穿过公路的EF部分的排管费用为每米2万元,设EF与AB所成的小于/的角为/.
(Ⅰ)求矩形区域ABCD内的排管费用W关于/的函数关系式;
(Ⅱ)求排管的最小费用及相应的角/.
(苏州2015届高三期初)18.(本小题满分16分)如图,有两条相交成60°角的直路XX(,YY(,交点是O,甲、乙分别在OX,OY上,起初甲离O点3,乙离O点1.后来甲沿XX(的方向,乙沿Y(Y的方向,同时用4的速度步行.
(1)起初两人的距离是多少?
(2)t 后两人的距离是多少?
(3)什么时候两人的距离最短?
18.解:(1)由余弦定理,得起初两人的距离为
. ··············4分
(2)设t 后两人的距离为d(t),则
当时,此时
··············8分
当时,此时
所以. ··············12分 (3)当()时,两人的距离最短. ············16分
解(I)如图,以河岸所在直线为 x 轴,
以过 M 垂直于的直线为 y 轴建立直角坐标系,
则可得点M (0, 10),点,
设点,
过作平行于 x 轴的直线,
作 关于 的对称点 ,
则,
所以
()即为所求。
(2设三段水管总长为 L,则 由( I )知
()
∴,
即方程在
上有解,故,,
解得,所以 L 的最小值为 21,此时对应的 (0, 8),
故,的方程为,令得,
即,从而,
答:满足题意的 P 点距河岸 5km,距小区 M 到河岸的垂线5 km,此时污水处理站到小区 M和 N 的水管长度分别为 10km 和 6km..
解:(1)过作的垂线,垂足为;过作的垂线,垂足为.
在中,,则
在中,,··············4分
由题意易得 ························6分
因此, ················7分
·············9分
(2)
令, ,因为,所以 ,······12分
设锐角满足,
当时,,单调递减;
当时,,单调递增.··················14分
所以当 ,总造价最小,最小值为,此时,,,因此当米时,能使总造价最小.··16分
(1)设半圆的半径为r, 可得2x+2πr=400,即x+πr=200, 矩形ABCD的面积为S=2xr=x?πr≤?()2=, 当且仅当x=πr=100m时,矩形的面积取得最大值m2; (2)设半圆的半径为r, 由题意可得πr2+2xr=,可得2x=-πr, 即有内圈周长c=2x+2πr=+πr, 由x≥80,可得-πr≥160, 解得0<πr≤90, 可得f(r)=+πr,f′(r)=π-, 即有f(r)在(0,]上递减, 即有πr=90,即x=80m时,周长c取得最小值340m.
17.(本题满分14分)
解:(1)∵半圆的半径为r,,∠OBC=90°.
∴在直角三角形OBC中,
,,∴.
∴. 2分
又∵∠BOG=,由半圆的对称性可知,∠HOA=,∴∠HOG=.
∴△HOG为等边三角形,∴HG=r,HE==.
∴. 4分
∴,其中.
7分
(2) ∵=. 9分
令,即,
解得:或(舍去). 11分
令,.
当时,,单调递增;
当时,,单调递减.
∴当时,取得最大值. 13分
答:当时,可使市民活动广场和停车场的面积总和最大. 14分
同课章节目录
