苏科版数学八年级上册6.1函数课件(21张PPT)
文档属性
| 名称 | 苏科版数学八年级上册6.1函数课件(21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-17 20:36:00 | ||
图片预览







文档简介
(共21张PPT)
苏科版数学八年级上册 第6章 一次函数
§6.1 函数(1)
“沙漏”是我国古代的一种计量时间的仪器,它根据一个容器里的细沙漏到另一个容器里的数量来计量时间.
沙漏
古代文明
北京时间2013年6月13日13时18分,天宫一号目标飞行器与神舟十号飞船成功实现自动交会对接.
太空之吻
现代文明
一列动车从常州驶向南京,在16:17到16:22这个时段,列车以200千米/时的速度匀速行驶.在列车行驶过程中,涉及到了哪些数量?
在某一变化过程中,数值保持不变的量叫做常量,可以取不同数值的量叫做变量.
1、新中国成立以来,我国已经进行了六次人口普查. 下表是我国六次人口普查的人口数统计表.
年份 人口数(亿)
1953 6.02
1964 7.23
1982 10.32
1990 11.60
2000 12.95
2010 13.71
(1)在这一变化过程中,有几个变量?分别是什么?
(2)在这一变化过程中,两个变量之间有什么关系?
随着 的变化而变化.
人口数
年份
人口数
年份
对于 的每一个值, 都有唯一的值与它对应.
年份
人口数
当 确定时, 也随着确定.
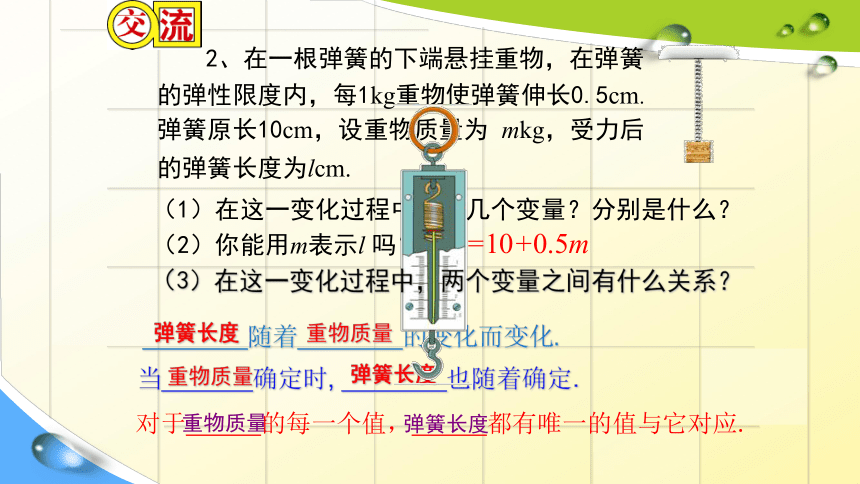
2、在一根弹簧的下端悬挂重物,在弹簧的弹性限度内,每1kg重物使弹簧伸长0.5cm. 弹簧原长10cm,设重物质量为 mkg,受力后的弹簧长度为lcm.
(1)在这一变化过程中,有几个变量?分别是什么?
(2)你能用m表示l 吗?
重物质量
弹簧长度
重物质量
弹簧长度
l=10+0.5m
重物质量
弹簧长度
随着 的变化而变化.
对于 的每一个值, 都有唯一的值与它对应.
当 确定时, 也随着确定.
(3)在这一变化过程中,两个变量之间有什么关系?
时间t(时)
8
10
2
4
6
12
14
16
18
20
22
24
0
温度T(?C)
2
4
6
8
-2
-4
0
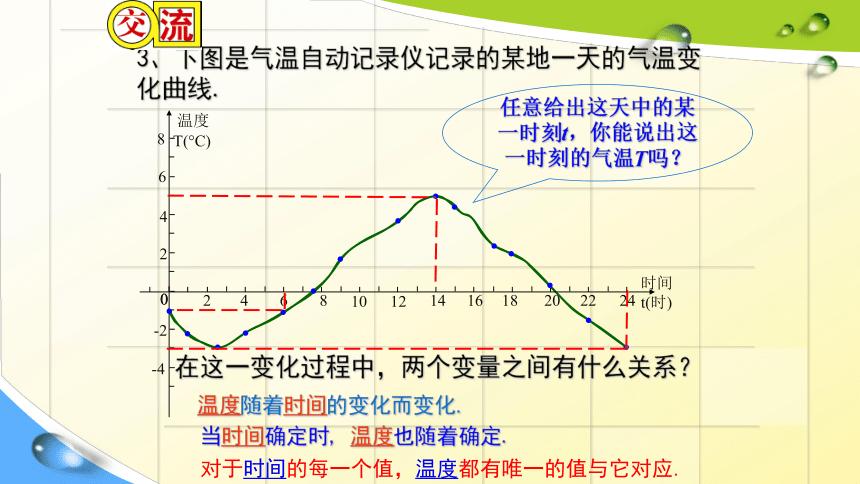
3、下图是气温自动记录仪记录的某地一天的气温变化曲线.
温度随着时间的变化而变化.
任意给出这天中的某一时刻t,你能说出这一时刻的气温T吗?
对于时间的每一个值,温度都有唯一的值与它对应.
当时间确定时, 温度也随着确定.
在这一变化过程中,两个变量之间有什么关系?
上述的三个变化过程,有怎样的共同之处呢?
说一说
函数的定义
一般地, 在一个变化过程中的两个变量x和y, 如果对于x的每一个值, y都有唯一的值与它对应,那么我们称y是x的函数,x是自变量.
在函数的定义中,关键词是什么?
函数小史
function
莱布尼兹
(德国)
李善兰
(清代)
凡此变数函彼变数,则此为彼之函数 .
(这里的“函”有包含的意思.)
函数
翻译
上述三个实例中,谁是谁的函数?自变量是谁?
说一说
例1、用一根1m长的铁丝围成一个长方形.
(1)当长方形的宽为0.1m时,长为 m .
(2)当长方形的宽为0.2m时,长为 m .
(3)当长方形的宽为 x m时,长为 m .
(4)长方形的长y(m)是宽 x (m)的函数吗? 为什么?
长方形的长y是宽x的函数.
理由:在这个变化过程中,有两个变量x和y,并且对于x的每一个值,y都有唯一的值与它对应.
0.3
0.4
(0.5-x)
在学习了函数的概念后,同学们试着自己举一些函数的实例:
小明:
圆的半径为r,面积S是半径r的函数,r是自变量.
你认为他们说的正确吗?为什么?
小亮:
长方体的长是a,宽是b,高是4,长方体的体积V是长a的函数.
仿照范例,自己编一个表示函数关系的实例.
小组交流的要求:
1、每个人轮流说说自己编的函数实例,要求讲清谁是谁的函数?自变量是什么?
2、一个同学说的时候,其他同学判断这两个变量之间的关系是不是函数关系?
(注:推荐一名同学准备大班交流.)
例2、根据表格中的信息,回答问题:其中,x表示乘公交车的站数(站),y表示相应付的票价(元).
(1)y是x的函数吗?为什么?
x 1 2 3 4 5 6 7 8 9 10 11 12 13 14
y 1.0 1.0 1.0 1.0 1.2 1.2 1.5 1.5 1.5 1.8 1.8 1.8 2.0 2.0
(2)x是y的函数吗?为什么?
信件质量x/克 0< x ≤20 20< x ≤40 40< x ≤60
邮资y /元 0.80 1.20 1.60
在国内投寄平信应付邮资如下表:
变式:
(1)y是x的函数吗?为什么?
(2)x是y的函数吗?为什么?
1、本节课,我们经历了怎样的过程?你有哪些收获?
2、本节课,给你感受最深的是什么?你还有哪些困惑?
函数:研究变化规律的数学模型
生活
实例
数学模型
研究现实
建构
应用
作业:
2. 选做题:查阅关于函数的发展历史.
1. 必做题:课本第138页练习的第1、2题;
谢谢!
时间是一个常量,但对勤奋者来说,却是一个“变量”,我们应当在有限的时间内做出伟大的事业!
如图,搭一条小鱼需要8根火柴棒,每多搭一条小鱼就要增加6根火柴棒.如果搭n条小鱼所需火柴棒的根数为S,那么他们之间的关系为S=8+6(n-1).
函数与代数式、方程、不等式有着紧密的联系!
苏科版数学八年级上册 第6章 一次函数
§6.1 函数(1)
“沙漏”是我国古代的一种计量时间的仪器,它根据一个容器里的细沙漏到另一个容器里的数量来计量时间.
沙漏
古代文明
北京时间2013年6月13日13时18分,天宫一号目标飞行器与神舟十号飞船成功实现自动交会对接.
太空之吻
现代文明
一列动车从常州驶向南京,在16:17到16:22这个时段,列车以200千米/时的速度匀速行驶.在列车行驶过程中,涉及到了哪些数量?
在某一变化过程中,数值保持不变的量叫做常量,可以取不同数值的量叫做变量.
1、新中国成立以来,我国已经进行了六次人口普查. 下表是我国六次人口普查的人口数统计表.
年份 人口数(亿)
1953 6.02
1964 7.23
1982 10.32
1990 11.60
2000 12.95
2010 13.71
(1)在这一变化过程中,有几个变量?分别是什么?
(2)在这一变化过程中,两个变量之间有什么关系?
随着 的变化而变化.
人口数
年份
人口数
年份
对于 的每一个值, 都有唯一的值与它对应.
年份
人口数
当 确定时, 也随着确定.
2、在一根弹簧的下端悬挂重物,在弹簧的弹性限度内,每1kg重物使弹簧伸长0.5cm. 弹簧原长10cm,设重物质量为 mkg,受力后的弹簧长度为lcm.
(1)在这一变化过程中,有几个变量?分别是什么?
(2)你能用m表示l 吗?
重物质量
弹簧长度
重物质量
弹簧长度
l=10+0.5m
重物质量
弹簧长度
随着 的变化而变化.
对于 的每一个值, 都有唯一的值与它对应.
当 确定时, 也随着确定.
(3)在这一变化过程中,两个变量之间有什么关系?
时间t(时)
8
10
2
4
6
12
14
16
18
20
22
24
0
温度T(?C)
2
4
6
8
-2
-4
0
3、下图是气温自动记录仪记录的某地一天的气温变化曲线.
温度随着时间的变化而变化.
任意给出这天中的某一时刻t,你能说出这一时刻的气温T吗?
对于时间的每一个值,温度都有唯一的值与它对应.
当时间确定时, 温度也随着确定.
在这一变化过程中,两个变量之间有什么关系?
上述的三个变化过程,有怎样的共同之处呢?
说一说
函数的定义
一般地, 在一个变化过程中的两个变量x和y, 如果对于x的每一个值, y都有唯一的值与它对应,那么我们称y是x的函数,x是自变量.
在函数的定义中,关键词是什么?
函数小史
function
莱布尼兹
(德国)
李善兰
(清代)
凡此变数函彼变数,则此为彼之函数 .
(这里的“函”有包含的意思.)
函数
翻译
上述三个实例中,谁是谁的函数?自变量是谁?
说一说
例1、用一根1m长的铁丝围成一个长方形.
(1)当长方形的宽为0.1m时,长为 m .
(2)当长方形的宽为0.2m时,长为 m .
(3)当长方形的宽为 x m时,长为 m .
(4)长方形的长y(m)是宽 x (m)的函数吗? 为什么?
长方形的长y是宽x的函数.
理由:在这个变化过程中,有两个变量x和y,并且对于x的每一个值,y都有唯一的值与它对应.
0.3
0.4
(0.5-x)
在学习了函数的概念后,同学们试着自己举一些函数的实例:
小明:
圆的半径为r,面积S是半径r的函数,r是自变量.
你认为他们说的正确吗?为什么?
小亮:
长方体的长是a,宽是b,高是4,长方体的体积V是长a的函数.
仿照范例,自己编一个表示函数关系的实例.
小组交流的要求:
1、每个人轮流说说自己编的函数实例,要求讲清谁是谁的函数?自变量是什么?
2、一个同学说的时候,其他同学判断这两个变量之间的关系是不是函数关系?
(注:推荐一名同学准备大班交流.)
例2、根据表格中的信息,回答问题:其中,x表示乘公交车的站数(站),y表示相应付的票价(元).
(1)y是x的函数吗?为什么?
x 1 2 3 4 5 6 7 8 9 10 11 12 13 14
y 1.0 1.0 1.0 1.0 1.2 1.2 1.5 1.5 1.5 1.8 1.8 1.8 2.0 2.0
(2)x是y的函数吗?为什么?
信件质量x/克 0< x ≤20 20< x ≤40 40< x ≤60
邮资y /元 0.80 1.20 1.60
在国内投寄平信应付邮资如下表:
变式:
(1)y是x的函数吗?为什么?
(2)x是y的函数吗?为什么?
1、本节课,我们经历了怎样的过程?你有哪些收获?
2、本节课,给你感受最深的是什么?你还有哪些困惑?
函数:研究变化规律的数学模型
生活
实例
数学模型
研究现实
建构
应用
作业:
2. 选做题:查阅关于函数的发展历史.
1. 必做题:课本第138页练习的第1、2题;
谢谢!
时间是一个常量,但对勤奋者来说,却是一个“变量”,我们应当在有限的时间内做出伟大的事业!
如图,搭一条小鱼需要8根火柴棒,每多搭一条小鱼就要增加6根火柴棒.如果搭n条小鱼所需火柴棒的根数为S,那么他们之间的关系为S=8+6(n-1).
函数与代数式、方程、不等式有着紧密的联系!
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
