人教A版数学选修2—1 1.3 简单的逻辑联接词(共27张ppt)
文档属性
| 名称 | 人教A版数学选修2—1 1.3 简单的逻辑联接词(共27张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 218.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-18 00:00:00 | ||
图片预览







文档简介
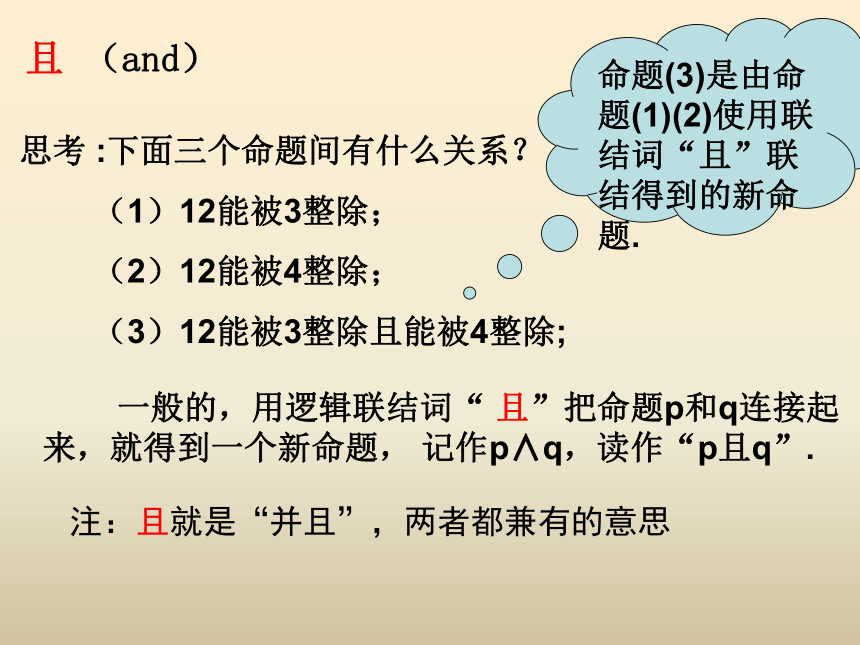
课件27张PPT。简单的逻辑联结词 在数学中常常要使用逻辑联结词“或”、“且”、“非”,它们与日常生活中这些词语所表达的含义和用法是不尽相同的,下面我们就分别介绍数学中使用联结词“或”、“且”、“非”联结命题时的含义与用法。 为了叙述简便,今后常用小写字母p,q,r,s,…表示命题。 一般的,用逻辑联结词“ 且”把命题p和q连接起来,就得到一个新命题, 记作p∧q,读作“p且q”.且 (and)命题(3)是由命题(1)(2)使用联结词“且”联结得到的新命题.
注:且就是“并且”,两者都兼有的意思例1 将下列命题用“且”联结成新命题
(1) p :菱形的对角线互相垂直,
q :菱形的对角线互相平分;
(2) p :35是15的倍数,
q :35是7的倍数。
(3) 命题p: 相似三角形的面积相等;
命题q: 相似三角形的周长相等;
解: p ∧q :相似三角形的面积相等且周长相等
解: p∧q : 菱形的对角线互相垂直且平分解: p∧q : 35是15的倍数且是7的倍数。真假假填空:一般地,我们规定:当p,q都是真命题时,p∧q是 ;当p,q 中有一个命题是假命题时,p∧q是 .
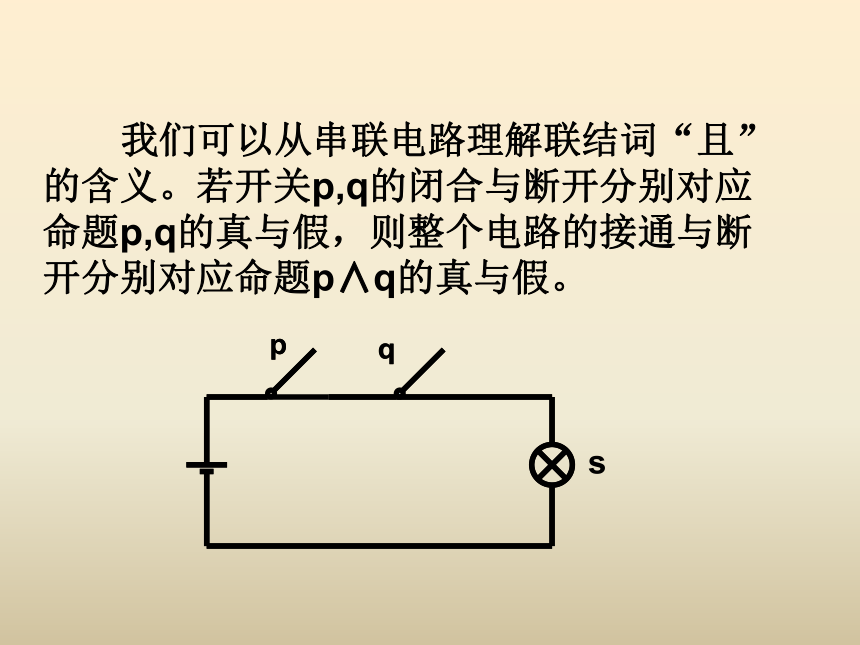
全真为真,有假即假. 真命题假命题命题p∧q的真假判断方法:假假假真 我们可以从串联电路理解联结词“且”的含义。若开关p,q的闭合与断开分别对应命题p,q的真与假,则整个电路的接通与断开分别对应命题p∧q的真与假。pqspq 逻辑联结词“且”的含义与集合中学过的哪个概念的意义相同呢? 对“且”的理解,可联想到集合中“交集”的概念.
A∩B={x︱x∈A且x∈B}中的“且”,是指“x∈A”、“x∈B”这两个条件都要满足的意思符号“∧”与“∩”开口都是向下 活动探究1思考 :下列三个命题间有什么关系?
(1)27是7的倍数;
(2)27是9的倍数;
(3)27是7的倍数 是9的倍数。或或一般地,用逻辑联结词“或 ”把命题p和命题q联结来,
就得到一个新命题,记作p∨q, 读作“p或q”注: “或”就是两者至少一个(可兼有),逻辑连接词中的“或”比日常生活中的“或”多了“可兼有”的意思,例如“你去或我去”理解为你去,我去,你我都去三种 或 (or)命题(3)是由命题(1)(2)使用联结词“或”联结得到的新命题.
例2 将下列命题用“或”联结成新命题
(1) p :菱形的对角线互相垂直,
q :菱形的对角线互相平分;
(2) p :35是15的倍数,
q :35是7的倍数。
(3) 命题p: 相似三角形的面积相等;
命题q: 相似三角形的周长相等;
解: p ∨q :相似三角形的面积相等或周长相等解: p∨q : 菱形的对角线互相垂直或平分。
解: p∨q : 35是15的倍数或是7的倍数。真假真 一般地,我们规定:当p,q两个命题中
有 个命题是真命题时,p∨q是 命题;
当p,q两个命题都是假命题时,p∨q
是 命题.
有真即真, 全假为假. 一真假命题p∨q的真假判断方法:假真真真我们可以从并联电路理解联结词“或”的含义。若开关p,q的闭合与断开分别对应命题p,q的真与假,则整个电路的接通与断开分别对应命题p∨q的真与假。pqs 逻辑联结词“或”的含义与集合中学过的哪个概念的意义相同呢?活动探究2符号“∨”与“∪”开口都是向上 下列两组命题间有什么关系?
(1)35能被5整除;
(2)35不能被5整除.
(3)方程 x2+x+1=0有实数根;
(4)方程 x2+x+1=0无实数根 非 (not) 一般地,对一个命题p全盘否定,就得到一个新命题,记作? p,读作“非p”或“p的否定”.命题(2)是命题(1)的否定,命题(4)是命题(3)的否定.填写下表 注意“非”对关键词的否定方式不等于不大于不小于不是不都是至少有两个一个都没有填空:当p为真命题时,则┐p为 ;当p为假命题时,则┐p为 .
思考:命题P与┐p的真假关系如何?
真假相反p与┐p真假性相反真命题假命题 假真 对“非”的理解,可联想到集合中的“补集”概念,若命题p对应于集合P,则命题非p就对应着集合P在全集U中的补集CUP. 逻辑联结词“非”的含义与集合中学过的哪个概念的意义相同呢?活动探究3例4:写出命题p: “正方形的四条边相等”的否定与它的否命题命题┓p:
p的否命题:
正方形的四条边不相等.若一个四边形不是正方形,则它的
四条边不相等.(1)原命题“若P则q” 的形式,
(2)命题的否定(非)的真假性与原命题 ;而否命题的真假性与原命题 .命题的否定与否命题的区别它的否定:“若p,则?q”它的否命题:“若┓p,则┓q”.相反无关.1.命题“方程 的解是 ”中,使用逻辑词的情况是( )
A.没有使用逻辑联结词
B.使用了逻辑联结词“或”
C. 使用了逻辑联结词“且”
D. 使用了逻辑联结词“或”与“且”B练习 2.在一次模拟射击游戏中,小李连续射击了两次,设命题p:“第一次射击中靶”,命题q:“第二次射击中靶”,试用,p、q及逻辑联结词“或”“且”“非”表示下列命题:
(1)两次射击均中靶;
(2)两次射击至少有一次中靶.p∧qp∨q3.在下列命题中
( 1)命题“ 属于集合 且属于集合 ”
(2)命题“3是偶数或奇数”
(3)命题“不等式 没有实数解”
其中,真命题为_____________.(2)
4.若命题“﹁p”与命题“p∨q”都是真命题,那么( )
A.命题p与命题q的真假相同
B.命题q一定是真命题
C.命题q不一定是真命题
D.命题p不一定是真命题
5. 命题p:“不等式 的解集为
”;命题q:“不等式 的解集为 ”,则 ( )
A.p真q假
B.p假q真
C.命题“p且q”为真
D.命题“p或q”为假 D6.设命题p:实数x满足 ,
命题q:实数x满足 ,
若p且q为真,则实数 x的取值
范围为 . 7.设p:方程x2+mx+1=0有两个不等的负根,q:方程4x2+4(m-2)x+1=0无实根.若p或q为真,p且q为假,求m的取值范围.解:若方程x2+mx+1=0有两个不等的负根 即 p: m>2若方程4x2+4(m-2)x+1=0无实根则?=16(m-2)2-16<0,即1(2)正确应用逻辑联结词“且、或、非”解决问题
(3)掌握真值表并会应用真值表解决问题
注:且就是“并且”,两者都兼有的意思例1 将下列命题用“且”联结成新命题
(1) p :菱形的对角线互相垂直,
q :菱形的对角线互相平分;
(2) p :35是15的倍数,
q :35是7的倍数。
(3) 命题p: 相似三角形的面积相等;
命题q: 相似三角形的周长相等;
解: p ∧q :相似三角形的面积相等且周长相等
解: p∧q : 菱形的对角线互相垂直且平分解: p∧q : 35是15的倍数且是7的倍数。真假假填空:一般地,我们规定:当p,q都是真命题时,p∧q是 ;当p,q 中有一个命题是假命题时,p∧q是 .
全真为真,有假即假. 真命题假命题命题p∧q的真假判断方法:假假假真 我们可以从串联电路理解联结词“且”的含义。若开关p,q的闭合与断开分别对应命题p,q的真与假,则整个电路的接通与断开分别对应命题p∧q的真与假。pqspq 逻辑联结词“且”的含义与集合中学过的哪个概念的意义相同呢? 对“且”的理解,可联想到集合中“交集”的概念.
A∩B={x︱x∈A且x∈B}中的“且”,是指“x∈A”、“x∈B”这两个条件都要满足的意思符号“∧”与“∩”开口都是向下 活动探究1思考 :下列三个命题间有什么关系?
(1)27是7的倍数;
(2)27是9的倍数;
(3)27是7的倍数 是9的倍数。或或一般地,用逻辑联结词“或 ”把命题p和命题q联结来,
就得到一个新命题,记作p∨q, 读作“p或q”注: “或”就是两者至少一个(可兼有),逻辑连接词中的“或”比日常生活中的“或”多了“可兼有”的意思,例如“你去或我去”理解为你去,我去,你我都去三种 或 (or)命题(3)是由命题(1)(2)使用联结词“或”联结得到的新命题.
例2 将下列命题用“或”联结成新命题
(1) p :菱形的对角线互相垂直,
q :菱形的对角线互相平分;
(2) p :35是15的倍数,
q :35是7的倍数。
(3) 命题p: 相似三角形的面积相等;
命题q: 相似三角形的周长相等;
解: p ∨q :相似三角形的面积相等或周长相等解: p∨q : 菱形的对角线互相垂直或平分。
解: p∨q : 35是15的倍数或是7的倍数。真假真 一般地,我们规定:当p,q两个命题中
有 个命题是真命题时,p∨q是 命题;
当p,q两个命题都是假命题时,p∨q
是 命题.
有真即真, 全假为假. 一真假命题p∨q的真假判断方法:假真真真我们可以从并联电路理解联结词“或”的含义。若开关p,q的闭合与断开分别对应命题p,q的真与假,则整个电路的接通与断开分别对应命题p∨q的真与假。pqs 逻辑联结词“或”的含义与集合中学过的哪个概念的意义相同呢?活动探究2符号“∨”与“∪”开口都是向上 下列两组命题间有什么关系?
(1)35能被5整除;
(2)35不能被5整除.
(3)方程 x2+x+1=0有实数根;
(4)方程 x2+x+1=0无实数根 非 (not) 一般地,对一个命题p全盘否定,就得到一个新命题,记作? p,读作“非p”或“p的否定”.命题(2)是命题(1)的否定,命题(4)是命题(3)的否定.填写下表 注意“非”对关键词的否定方式不等于不大于不小于不是不都是至少有两个一个都没有填空:当p为真命题时,则┐p为 ;当p为假命题时,则┐p为 .
思考:命题P与┐p的真假关系如何?
真假相反p与┐p真假性相反真命题假命题 假真 对“非”的理解,可联想到集合中的“补集”概念,若命题p对应于集合P,则命题非p就对应着集合P在全集U中的补集CUP. 逻辑联结词“非”的含义与集合中学过的哪个概念的意义相同呢?活动探究3例4:写出命题p: “正方形的四条边相等”的否定与它的否命题命题┓p:
p的否命题:
正方形的四条边不相等.若一个四边形不是正方形,则它的
四条边不相等.(1)原命题“若P则q” 的形式,
(2)命题的否定(非)的真假性与原命题 ;而否命题的真假性与原命题 .命题的否定与否命题的区别它的否定:“若p,则?q”它的否命题:“若┓p,则┓q”.相反无关.1.命题“方程 的解是 ”中,使用逻辑词的情况是( )
A.没有使用逻辑联结词
B.使用了逻辑联结词“或”
C. 使用了逻辑联结词“且”
D. 使用了逻辑联结词“或”与“且”B练习 2.在一次模拟射击游戏中,小李连续射击了两次,设命题p:“第一次射击中靶”,命题q:“第二次射击中靶”,试用,p、q及逻辑联结词“或”“且”“非”表示下列命题:
(1)两次射击均中靶;
(2)两次射击至少有一次中靶.p∧qp∨q3.在下列命题中
( 1)命题“ 属于集合 且属于集合 ”
(2)命题“3是偶数或奇数”
(3)命题“不等式 没有实数解”
其中,真命题为_____________.(2)
4.若命题“﹁p”与命题“p∨q”都是真命题,那么( )
A.命题p与命题q的真假相同
B.命题q一定是真命题
C.命题q不一定是真命题
D.命题p不一定是真命题
5. 命题p:“不等式 的解集为
”;命题q:“不等式 的解集为 ”,则 ( )
A.p真q假
B.p假q真
C.命题“p且q”为真
D.命题“p或q”为假 D6.设命题p:实数x满足 ,
命题q:实数x满足 ,
若p且q为真,则实数 x的取值
范围为 . 7.设p:方程x2+mx+1=0有两个不等的负根,q:方程4x2+4(m-2)x+1=0无实根.若p或q为真,p且q为假,求m的取值范围.解:若方程x2+mx+1=0有两个不等的负根 即 p: m>2若方程4x2+4(m-2)x+1=0无实根则?=16(m-2)2-16<0,即1
(3)掌握真值表并会应用真值表解决问题
