人教版数学必修5 1.2 应用举例(测量高度角度)(共18张ppt)
文档属性
| 名称 | 人教版数学必修5 1.2 应用举例(测量高度角度)(共18张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 381.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-18 13:02:12 | ||
图片预览




文档简介
课件18张PPT。 解三角形的应用举例(二)
—测量高度、角度1 知识与技能
能用正、余弦定理等知识解决与高度、角度有关的三角形问题;
2 过程与方法
通过合作探究,解决例题及习题,学习数学建模的方法,提高分析问题、解决问题的能力;
3 情感、态度与价值观
体会这类测量问题在某一特定情境和条件限制下的一个测量方案,感受数学的应用价值,提高学习兴趣。
重点:画出示意图,分析已知与所求,解三角形。
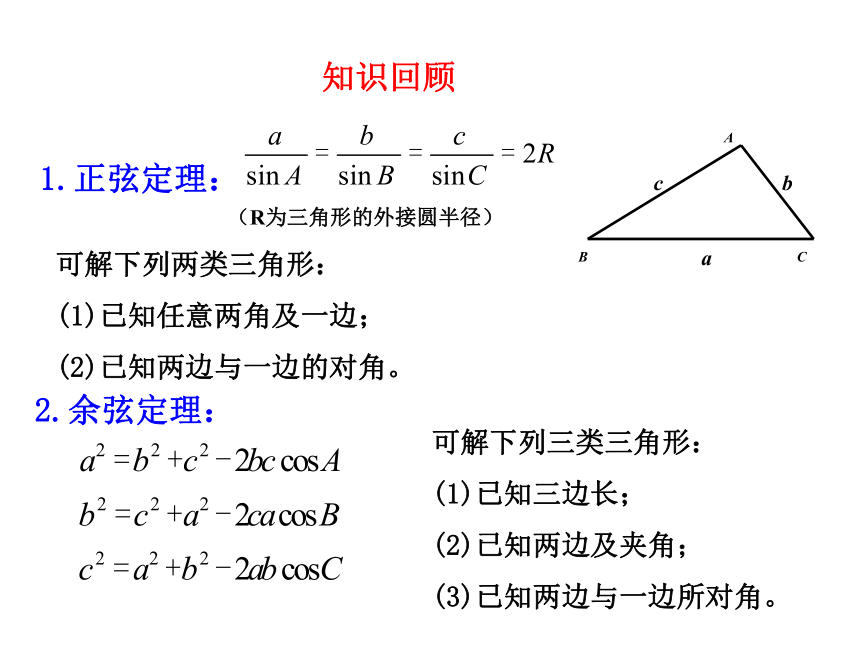
难点:根据题意建立数学模型,画出示意图。学习目标1.正弦定理:2.余弦定理:知识回顾可解下列两类三角形:
(1)已知任意两角及一边;
(2)已知两边与一边的对角。可解下列三类三角形:
(1)已知三边长;
(2)已知两边及夹角;
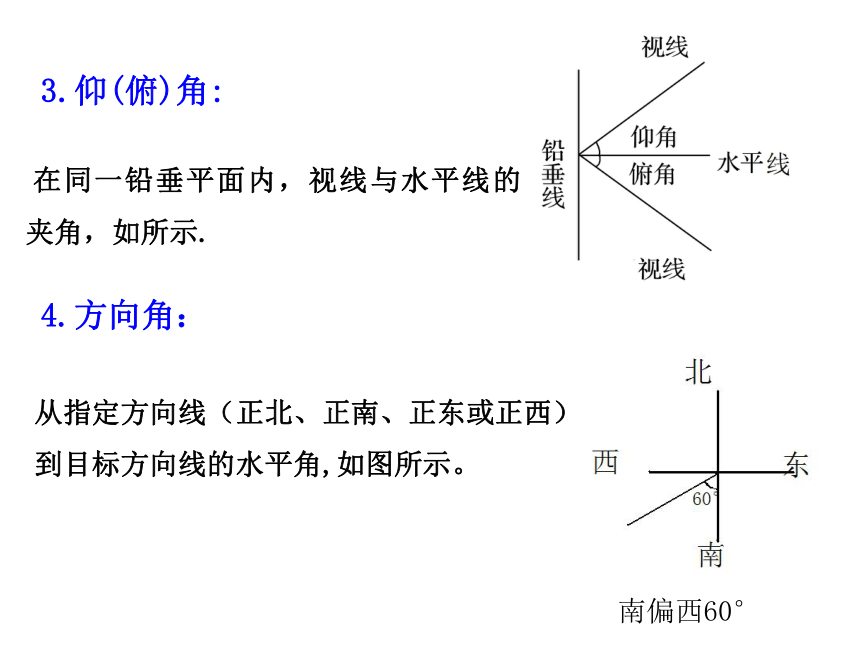
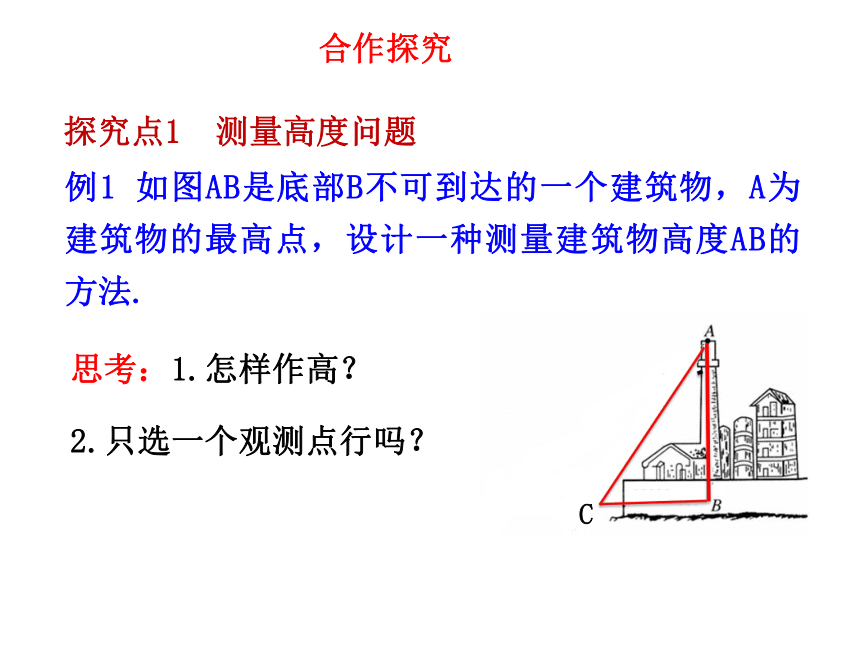
(3)已知两边与一边所对角。3.仰(俯)角: 4.方向角:1.生活中,人们怎样测量底部不可到达的物体的高度呢?2.海面上,如何确保轮船不迷失方向,保持航速和航向呢?情境引入建立数学模型,转化为解三角形的问题解决。探究点1 测量高度问题例1 如图AB是底部B不可到达的一个建筑物,A为建筑物的最高点,设计一种测量建筑物高度AB的方法.思考:1.怎样作高?
2.只选一个观测点行吗?合作探究C 如图某同学选择H、G两点,使H、G、B三点在同一条水平线上,在H,G两点用测角仪器测得A的仰角分别是α,β,CD=a,且测角仪器的高是h,则AB=?法一法二AE+EB=AE+hAE 解决高度问题步骤:
(1)作高:作与地平面垂直的线段表示高度;
(2)画图:分清仰角、俯角,画示意图(必含直角三角形);
(3)求解:分析已知与所求,解三角形得实际问题的解.悟感悟:练习1.如图某人选择水平面上的两点C、D,AB⊥面BCD,CD=800m,在C点测得A的仰角∠ACB=45°,∠BCD=120°,又在D点测得∠BDC=45°,求AB.解答探究点2 测量角度问题 解决航海问题步骤:
(1)定位: 选择好不动点,
(2)画图:搞清方向角,画出示意图,
(3)求解:分析已知与所求,解三角形,得实际问题的解。感悟答:缉私船航向为北偏东75°,1小时即可追上。∠C=30°=∠BAC,BC=AB=10,t=1,
45 °+30 °=75 °答:缉私船航向为北偏东75°,1小时即可追上。1.如图,在山顶铁塔上B处测得地面上一点A的俯角为α=60°,在塔底C处测得A处的俯角为β=30°,已知铁塔BC部分的高为100m,求山高CD.随堂检测 2.已知两座灯塔A和B与海洋观测站C的距离相等,灯塔A在观测站C的北偏东40°,灯塔B在观测站C的南偏东60 °,则灯塔A在灯塔B的( )A.北偏东10 ° B.北偏西10°
C.南偏东10° D.南偏西10°50mB解析二解析一(1)审题:准确理解题意,分清已知与所求;
(2)画图:根据题意画出示意图,并注明已知条件;
(3)求解:分析与问题有关的一个或者几个三角形,运用正、余弦定理等知识正确求解,并作答。课堂小结1.解三角形应用题的一般步骤:实际问题2.解决实际问题的基本思路
—测量高度、角度1 知识与技能
能用正、余弦定理等知识解决与高度、角度有关的三角形问题;
2 过程与方法
通过合作探究,解决例题及习题,学习数学建模的方法,提高分析问题、解决问题的能力;
3 情感、态度与价值观
体会这类测量问题在某一特定情境和条件限制下的一个测量方案,感受数学的应用价值,提高学习兴趣。
重点:画出示意图,分析已知与所求,解三角形。
难点:根据题意建立数学模型,画出示意图。学习目标1.正弦定理:2.余弦定理:知识回顾可解下列两类三角形:
(1)已知任意两角及一边;
(2)已知两边与一边的对角。可解下列三类三角形:
(1)已知三边长;
(2)已知两边及夹角;
(3)已知两边与一边所对角。3.仰(俯)角: 4.方向角:1.生活中,人们怎样测量底部不可到达的物体的高度呢?2.海面上,如何确保轮船不迷失方向,保持航速和航向呢?情境引入建立数学模型,转化为解三角形的问题解决。探究点1 测量高度问题例1 如图AB是底部B不可到达的一个建筑物,A为建筑物的最高点,设计一种测量建筑物高度AB的方法.思考:1.怎样作高?
2.只选一个观测点行吗?合作探究C 如图某同学选择H、G两点,使H、G、B三点在同一条水平线上,在H,G两点用测角仪器测得A的仰角分别是α,β,CD=a,且测角仪器的高是h,则AB=?法一法二AE+EB=AE+hAE 解决高度问题步骤:
(1)作高:作与地平面垂直的线段表示高度;
(2)画图:分清仰角、俯角,画示意图(必含直角三角形);
(3)求解:分析已知与所求,解三角形得实际问题的解.悟感悟:练习1.如图某人选择水平面上的两点C、D,AB⊥面BCD,CD=800m,在C点测得A的仰角∠ACB=45°,∠BCD=120°,又在D点测得∠BDC=45°,求AB.解答探究点2 测量角度问题 解决航海问题步骤:
(1)定位: 选择好不动点,
(2)画图:搞清方向角,画出示意图,
(3)求解:分析已知与所求,解三角形,得实际问题的解。感悟答:缉私船航向为北偏东75°,1小时即可追上。∠C=30°=∠BAC,BC=AB=10,t=1,
45 °+30 °=75 °答:缉私船航向为北偏东75°,1小时即可追上。1.如图,在山顶铁塔上B处测得地面上一点A的俯角为α=60°,在塔底C处测得A处的俯角为β=30°,已知铁塔BC部分的高为100m,求山高CD.随堂检测 2.已知两座灯塔A和B与海洋观测站C的距离相等,灯塔A在观测站C的北偏东40°,灯塔B在观测站C的南偏东60 °,则灯塔A在灯塔B的( )A.北偏东10 ° B.北偏西10°
C.南偏东10° D.南偏西10°50mB解析二解析一(1)审题:准确理解题意,分清已知与所求;
(2)画图:根据题意画出示意图,并注明已知条件;
(3)求解:分析与问题有关的一个或者几个三角形,运用正、余弦定理等知识正确求解,并作答。课堂小结1.解三角形应用题的一般步骤:实际问题2.解决实际问题的基本思路
