人教A版数学选修2—1 2.4.2 抛物线的简单几何性质(20张PPT)
文档属性
| 名称 | 人教A版数学选修2—1 2.4.2 抛物线的简单几何性质(20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 699.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-18 13:09:04 | ||
图片预览







文档简介
课件20张PPT。抛物线的简单几何性质目标理解并掌握抛物线的简单几何性质重点抛物线的几何性质与椭圆、双曲线的比较难点能利用抛物线的性质解决有关焦点弦的问题复习巩固:抛物线的定义是什么?
抛物线的标准方程、焦点坐标、准线方程是什么?解析:
1.抛物线的定义:平面内与一个定点F和一条定直线L的距离相等的点的轨迹叫做抛物线。点F→焦点,直线L→准线
y2 = 2px
(p>0)y2 = -2px
(p>0)x2 = 2py
(p>0)x2 = -2py
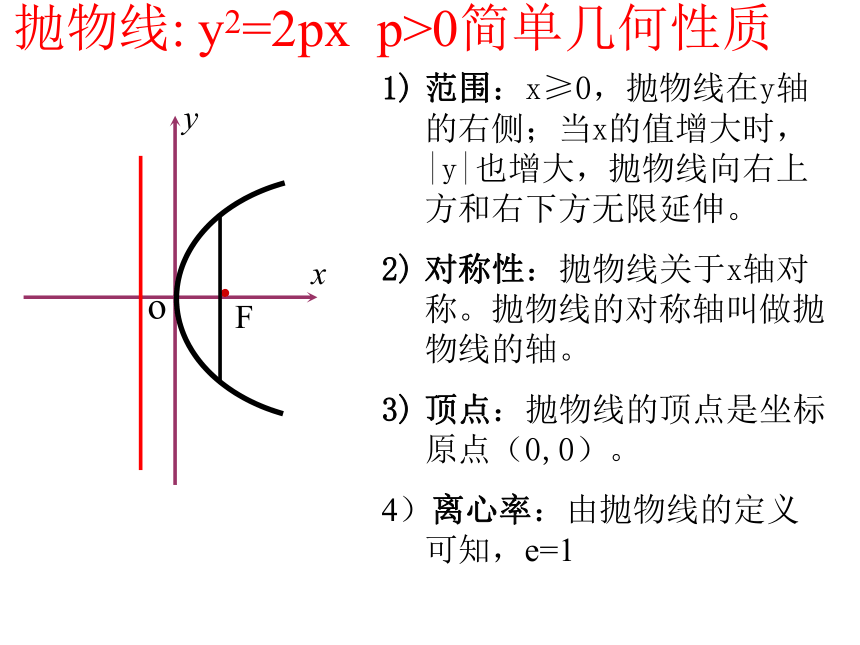
(p>0)问题引入我们已经学习了椭圆及双曲线的几何性质,请同学们回忆一下,是从哪几个方面研究的?类比来探究抛物线的几何性质。抛物线: y2=2px p>0简单几何性质范围:x≥0,抛物线在y轴的右侧;当x的值增大时,|y|也增大,抛物线向右上方和右下方无限延伸。
对称性:抛物线关于x轴对称。抛物线的对称轴叫做抛物线的轴。
顶点:抛物线的顶点是坐标原点(0,0)。
4)离心率:由抛物线的定义可知,e=1 y2 = 2px
(p>0)y2 = -2px
(p>0)x2 = 2py
(p>0)x2 = -2py
(p>0)x≥0
y∈Rx≤0
y∈Ry≥0
x∈Ry ≤ 0
x∈R(0,0)x轴y轴1特点:1.抛物线只位于半个坐标平面内,虽然它可以无限延伸,但它没有渐近线;2.抛物线只有一条对称轴,没有
对称中心;3.抛物线只有一个顶点、
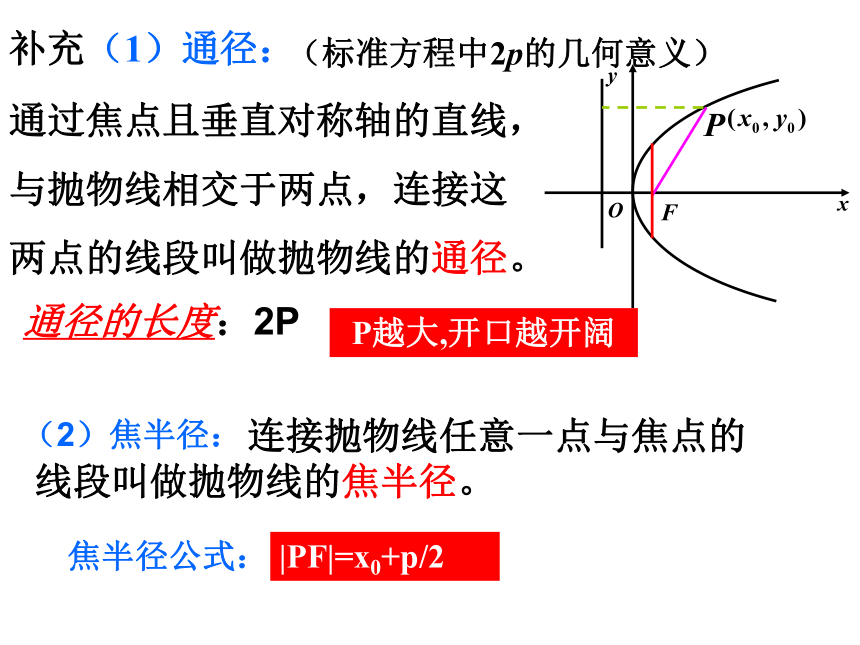
一个焦点、一条准线;4.抛物线的离心率是确定的,为1;思考:抛物线标准方程中的p对抛物线开口的影响.补充(1)通径:通过焦点且垂直对称轴的直线,
与抛物线相交于两点,连接这
两点的线段叫做抛物线的通径。|PF|=x0+p/2FP通径的长度:2PP越大,开口越开阔(2)焦半径: 连接抛物线任意一点与焦点的线段叫做抛物线的焦半径。焦半径公式:(标准方程中2p的几何意义) 例1:已知抛物线关于x轴对称,它的顶点在坐标原点,并且经过点M(2, ),求它的标准方程。典例评析: 变式练习:已知抛物线关于坐标轴对称,它的顶点在坐标原点,并且经过点M(2, ),求它的标准方程。例2 .斜率为1的直线L经过抛物线 的焦点F,且与抛物线相交于A,B两点,求线段AB的长. y2 = 4x解法一:由已知得抛物线的焦点为F(1,0),所以直线AB的方程为y=x-1例2 斜率为1的直线L经过抛物线 的焦点F,且与抛物线相交于A,B两点,求线段AB的长. y2 = 4x解法二:由已知得抛物线的焦点为F(1,0),所以直线AB的方程为y=x-1例2.斜率为l的直线L经过抛物线 的焦点F,且与抛物线相交于A,B两点,求线段AB的长. y2 = 4x例3 . 直线l经过抛物线y2=2px(p>0)的焦点,且与抛物线相交于A(x1,y1)、B(x2,y2)两点,求证:
1) x1x2 = 2) y1y2=-p2.拓展提升:小试牛刀:1、 设抛物线的顶点在原点,准线方程为x=-2,则抛物线的方程是( )
A. y2=-8x, B. y2=8x, C. y2=-4x, D.
2. 已知抛物线的顶点在原点,对称
轴为x轴,焦点在直线3x-4y-12=0上,那
么抛物线通径长是 y2 = 4x乘胜追击:3.已知抛物线的对称轴为x轴,抛物线上一点M(-3,m)到焦点的距离为5,求m的值。课堂小结:1.掌握抛物线的几何性质:范围、对称性、顶点、离心率、通径;
2.会利用抛物线的几何性质求抛物线的标准方程、焦点坐标及解决其它问题;3.注重数形结合思想。思考: 过抛物线y2=2px的焦点F任作一条直线m,交抛物线于A、B两点,求证:以AB为直径的圆和这抛物线的准线相切.分析:运用抛物线的定义和平面几何知识来证比较简捷.
抛物线的标准方程、焦点坐标、准线方程是什么?解析:
1.抛物线的定义:平面内与一个定点F和一条定直线L的距离相等的点的轨迹叫做抛物线。点F→焦点,直线L→准线
y2 = 2px
(p>0)y2 = -2px
(p>0)x2 = 2py
(p>0)x2 = -2py
(p>0)问题引入我们已经学习了椭圆及双曲线的几何性质,请同学们回忆一下,是从哪几个方面研究的?类比来探究抛物线的几何性质。抛物线: y2=2px p>0简单几何性质范围:x≥0,抛物线在y轴的右侧;当x的值增大时,|y|也增大,抛物线向右上方和右下方无限延伸。
对称性:抛物线关于x轴对称。抛物线的对称轴叫做抛物线的轴。
顶点:抛物线的顶点是坐标原点(0,0)。
4)离心率:由抛物线的定义可知,e=1 y2 = 2px
(p>0)y2 = -2px
(p>0)x2 = 2py
(p>0)x2 = -2py
(p>0)x≥0
y∈Rx≤0
y∈Ry≥0
x∈Ry ≤ 0
x∈R(0,0)x轴y轴1特点:1.抛物线只位于半个坐标平面内,虽然它可以无限延伸,但它没有渐近线;2.抛物线只有一条对称轴,没有
对称中心;3.抛物线只有一个顶点、
一个焦点、一条准线;4.抛物线的离心率是确定的,为1;思考:抛物线标准方程中的p对抛物线开口的影响.补充(1)通径:通过焦点且垂直对称轴的直线,
与抛物线相交于两点,连接这
两点的线段叫做抛物线的通径。|PF|=x0+p/2FP通径的长度:2PP越大,开口越开阔(2)焦半径: 连接抛物线任意一点与焦点的线段叫做抛物线的焦半径。焦半径公式:(标准方程中2p的几何意义) 例1:已知抛物线关于x轴对称,它的顶点在坐标原点,并且经过点M(2, ),求它的标准方程。典例评析: 变式练习:已知抛物线关于坐标轴对称,它的顶点在坐标原点,并且经过点M(2, ),求它的标准方程。例2 .斜率为1的直线L经过抛物线 的焦点F,且与抛物线相交于A,B两点,求线段AB的长. y2 = 4x解法一:由已知得抛物线的焦点为F(1,0),所以直线AB的方程为y=x-1例2 斜率为1的直线L经过抛物线 的焦点F,且与抛物线相交于A,B两点,求线段AB的长. y2 = 4x解法二:由已知得抛物线的焦点为F(1,0),所以直线AB的方程为y=x-1例2.斜率为l的直线L经过抛物线 的焦点F,且与抛物线相交于A,B两点,求线段AB的长. y2 = 4x例3 . 直线l经过抛物线y2=2px(p>0)的焦点,且与抛物线相交于A(x1,y1)、B(x2,y2)两点,求证:
1) x1x2 = 2) y1y2=-p2.拓展提升:小试牛刀:1、 设抛物线的顶点在原点,准线方程为x=-2,则抛物线的方程是( )
A. y2=-8x, B. y2=8x, C. y2=-4x, D.
2. 已知抛物线的顶点在原点,对称
轴为x轴,焦点在直线3x-4y-12=0上,那
么抛物线通径长是 y2 = 4x乘胜追击:3.已知抛物线的对称轴为x轴,抛物线上一点M(-3,m)到焦点的距离为5,求m的值。课堂小结:1.掌握抛物线的几何性质:范围、对称性、顶点、离心率、通径;
2.会利用抛物线的几何性质求抛物线的标准方程、焦点坐标及解决其它问题;3.注重数形结合思想。思考: 过抛物线y2=2px的焦点F任作一条直线m,交抛物线于A、B两点,求证:以AB为直径的圆和这抛物线的准线相切.分析:运用抛物线的定义和平面几何知识来证比较简捷.
