2.1 有理数 教案（表格式）

2.1　有理数
课题
1　有理数
授课人
教
学
目
标
知识技能
1.理解正、负数的概念，会判断一个数是正数还是负数；
2.会用正负数表示具有相反意义的量；
3.能按一定的标准对有理数进行分类．
数学思考
经历用正负数表示具有相反意义的量的过程，体会负数是实际生活的需要．
问题解决
借助生活中的实例，理解有理数的含义，体会负数引入的必要性和有理数应用的广泛性，培养学生学会分类讨论的数学思想.
情感态度
在负数概念的形成过程中，培养观察、归纳与概括的能力，提高学生的语言表达能力，培养学生的“数感”，渗透分类讨论思想和集合思想，并通过正负数表示具有相反意义的量，体会数学知识与生活的密切联系．
教学
重点
　　能理解正负数的概念，会判断一个数是正数还是负数．
教学
难点
　　会用正负数表示具有相反意义的量；有理数的分类及其分类的标准．
授课
类型
新授课
课时
第一课时
教具
多媒体课件
教学活动
教学
步骤
师生活动
设计意图
回顾
　　问题1：我们一起回忆一下，小学里已经学过哪些类型的数？
学生回答后，教师指出：小学里学过的数可以分为三类：整数、分数和零(小数包括在分数之中)，它们都是由于实际需要而产生的.
通过提供学生熟悉的实际生活情景引导学生回顾小学有关数的知识，了解生活当中的数学知识，体会“数”的实际意义，理解数学与生活息息相关.
活动
一：
创设
情境
导入
新课
　　你能用小学学过的数表示下列数吗？
图2－1－
处理方式：让学生回顾小学学过的数，通过多媒体展示，让学生发现出现了新的需要表示的数，从而引入具有相反意义的量，继而引入本节课内容.
问题3：同学们能举类似的例子吗？
处理方式：通过交流讨论，积极发言，发现生活中的数学知识，教师适当点评．
结合已有的知识经验，和生活常识，通过问题的形式引导学生发现“新数”进而引入课题.
让学生发现生活中到处存在数学知识，提高学生学习的兴趣.
活动
二：
实践
探究
交流
新知
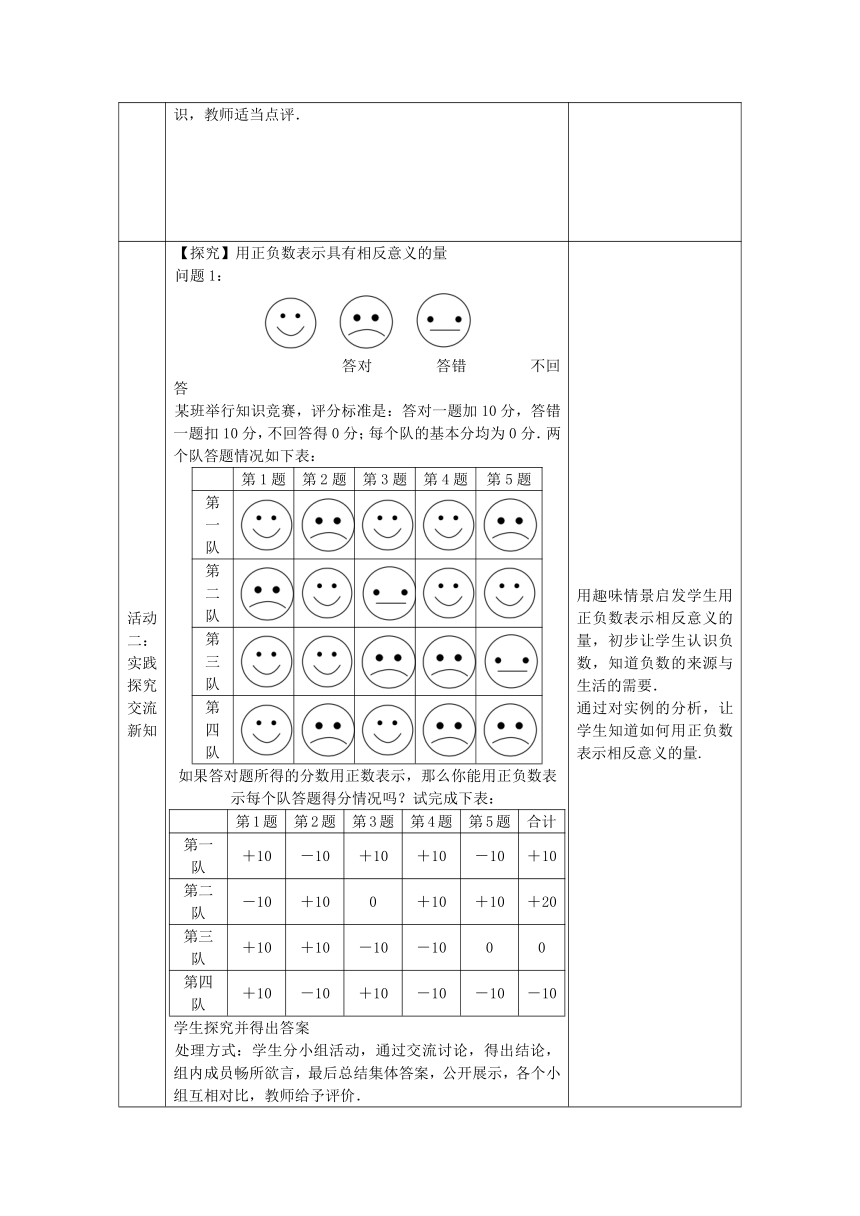
【探究】用正负数表示具有相反意义的量
问题1：

答对 答错 不回答
某班举行知识竞赛，评分标准是：答对一题加10分，答错一题扣10分，不回答得0分；每个队的基本分均为0分．两个队答题情况如下表：
第1题
第2题
第3题
第4题
第5题
第一队
第二队
第三队
第四队
如果答对题所得的分数用正数表示，那么你能用正负数表示每个队答题得分情况吗？试完成下表：
第1题
第2题
第3题
第4题
第5题
合计
第一队
＋10
－10
＋10
＋10
－10
＋10
第二队
－10
＋10
0
＋10
＋10
＋20
第三队
＋10
＋10
－10
－10
0
0
第四队
＋10
－10
＋10
－10
－10
－10
学生探究并得出答案
处理方式：学生分小组活动，通过交流讨论，得出结论，组内成员畅所欲言，最后总结集体答案，公开展示，各个小组互相对比，教师给予评价．
用趣味情景启发学生用正负数表示相反意义的量，初步让学生认识负数，知道负数的来源与生活的需要．
通过对实例的分析，让学生知道如何用正负数表示相反意义的量.
(续表)
活动
二：
实践
探究
交流
新知
　　问题2：生活中你见过带有“－”号的数吗？与同伴进行交流．
高于海平面8848米，记作＋8848米；低于海平面155米，记作－155米．
处理方式：让学生用同样的方法表示出前面例子中具有相反意义的量．教师引导学生认识0的位置．
例1　(1)在知识竞赛中，如果用＋10分表示加10分，那么扣20分怎样表示？
(2)某人转动转盘，如果用＋5圈表示沿逆时针方向转了5圈，那么沿顺时针方向转了12圈怎样表示？
(3)在某次乒乓球质量检测中，一只乒乓球超出标准质量0.02克记作＋0.02克，那么－0.03克表示什么？
处理方式：先让学生自己独立完成，教师巡视，点拨，然后分组交流，学生自己互相纠错，加深学生对正负数的理解，教师及时给予评价、点评．
变式训练
1．下列语句正确的是(　　)
A．“黑色”和“白色”是具有相反意义的量
B．“快”和“慢”是具有相反意义的量
C．“向北4.5米”和“向南4.5米”是具有相反意义的量
D．“＋15米”就表示向东走了15米
2．(1)如果零上5 ℃记作＋5 ℃，那么零下3 ℃记作________．
(2)东、西为两个相反方向，如果－4米表示一个物体向西运动4米，那么＋2米表示________，物体原地不动记作________．
(3)某仓库运进面粉7.5吨，那么运出3.8吨应记作________．
3．某商店出售的三种品牌的面粉袋上，分别标有(25±0.1)kg、(25±0.2)kg、(25±0.3)kg的字样，从中任意拿出两袋，质量最多相差(　　)
A．0.8 kg　　B．0.6 kg　　C．0.5 kg　　D．0.4 kg
处理方式：3个学生回答问题，并说明理由，其他学生给予补充，教师适当总结．
探究活动2：你能选定一个高度为标准，用正负数表示本班每位同学的身高与选定的身高标准的差异吗？你是怎样表示的？与同伴交流．
处理方式：让学生分组交流讨论，说出自己的答案以及理由，教师适当引导学生发现其中的差异，分析找出存在差异的原因是标准不同．
探究活动3：有理数的概念及分类
1．新的整数、分数概念：引进负数后，数的范围扩大了．过去我们说整数只包括正整数和零，引进负数后，正整数前加上负号的数叫做负整数，因而整数包括正整数、负整数和零，同样分数包括正分数、负分数．
整数和分数统称为有理数．
2．有理数的分类
问题：为了便于研究某些问题，常常需要将有理数进行分类，需要不同，分类的方法也常常不同，根据有理数的定义可将有理数分成两类：整数和分数．有理数还有没有其他的分类方法？
　　通过巩固练习加深对具有相反意义的量表示，进一步加强对负数的理解与应用．
通过讨论让学生进一步认识负数，并了解0的意义及作用．
学生在原有认知结构的基础上，将数扩充到了有理数的范围．通过练习使学生加深理解有理数的意义.
活动
二：
实践
探究
交流
新知
　　待学生思考后，请学生回答、评议、补充．
归纳总结：按有理数的符号分为三类：正有理数、负有理数和零，简称正数、负数和零，并指出，在有理数范围内，正数和零统称为非负数，并向学生强调：分类可以根据不同需要，用不同的分类标准，但必须对讨论对象不重不漏地分类．
教材拓展
1．通常把________数和________统称为非负数，把______数和________统称为非正数，把________数和________统称为非负整数(也叫自然数)，把______数和______统称为非正整数．
2．所以的________数组成正数集合，所以的________数组成负数集合，所以的________数组成整数集合，…
3．有限小数和________也是分数，例如：________．
活动
三：
开放
训练
体现
应用
【应用举例】
例1　某公司今年第一季度收入与支出情况如表所示(单位：万元)
请问：(1)该公司今年第一季度总收入与总支出各多少万元？
(2)如果收入用正数表示，则总收入与总支出应如何表示？
(3)该公司第一季度利润为多少万元？
月份
一月
二月
三月
收入
32
48
50
支出
12
13
10
通过例题进一步理解负数的实际意义，并通过练习进行针对性的巩固.
【拓展提升】
1.一种零件的长度在图纸上是(10±0.05)毫米，表示这种零件的标准尺寸是10毫米，加工要求最大不超过________毫米，最小不小于________毫米.
2.一批螺帽产品的内径要求可以有±0.02 mm的误差，现抽查5个样品，超过规定的毫米值记为正数，不足值记为负数，检查结果如表．则合乎要求的产品数量为(　　)
1
2
3
4
5
＋0.031
＋0.017
＋0.023
－0.021
－0.015
A.1个　　　B．2个　　　C．3个　　　D．5个
使学生在掌握基础知识的同时，进一步拓展，可使学生加深对引入负数的必要性的理解.
活动
四：
课堂
总结
反思
【当堂检测】
1．－3.782(　　)
A．是负数，不是分数　B．不是分数，是有理数
C．是负数，也是分数　 D．是分数，不是有理数
2．下面说法中正确的是(　　)
A．正整数和负整数统称为整数
B．分数不包括整数
C．正分数，负分数，负整数统称有理数
D．正整数和正分数统称正有理数
3．一种零件的长度在图纸上是(10±0.05)毫米，表示这种零件的标准尺寸是10毫米，加工要求最大不超过________毫米，最小不小于________毫米．
通过练习发现学生的本节课知识掌握情况，总结本节课的教学效果，并为课下辅导做好准备.
活动
四：
课堂
总结
反思
【板书设计】
2.1　有理数　　
投影
引例：
例1
练习
学　生　活　动　区
提纲挈领，重点突出.
【教学反思】
①[授课流程反思]
通过身边常见的生活情境，让学生感受到数不够用了，进而引入新课，容易调动学生的积极性，更能体现正负数的实际意义.
②[讲授效果反思]
通过对实际问题的探究感受正负数的实际意义，更好的理解负数的概念．同时结合学过的数将其分类，感受不同的标准会得到有理数不同的分类结果.
③[师生互动反思]
______________________________________________________
④[习题反思]
好题题号
错题题号
反思，更进一步提升.