2019版初中数学综合复习第10讲《一元一次不等式(组)》(含详细参考答案)
文档属性
| 名称 | 2019版初中数学综合复习第10讲《一元一次不等式(组)》(含详细参考答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 425.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-19 00:00:00 | ||
图片预览




文档简介
???学生用书+详细参考答案和教师用书???
把握命题趋势,提高复习效率,提升解题能力,打造中考高分!
2019版初中数学综合复习精品专题
第二章 方程与不等式
第十讲 一元一次不等式(组)
★★★核心知识回顾★★★
知识点一、不等式的基本概念
1.不等式:
用 连接起来的式子叫做不等式。
2.不等式的解:
使不等式成立的 的值,叫做不等式的解。
3.不等式的解集:
一个含有未知数的不等的解的 叫做不等式的解集。
(
◆◆◆
名师提醒
◆◆◆
(
1
)常见的不等号有五种:“≠”,“>”,“<”,“≥”,“≤”;
(
2
)
不等式的解与解集是不同的两个概念,不等式的解是单独的未知数的值,而解集是一个范围的未知数的值组成的集合,一般由无数个解组成
;
(
3
)
不等式的解集一般可以在数轴上
直观的
表示出来
,具体方法是:
①先确定边界点,解集包含边界点,用实心圆点表示;不包含边界点的,用空心圆圈表示;
②再确定方向:大向右,小向左
。
)
知识点二、不等式的基本性质:
基本性质1:
不等式两边都加上(或减去)同一个 或同一个 不等号的方向 ,即:若a基本性质2:
不等式两边都乘以(或除以)同一个 不等号的方向 ,即:若a0则a c bc(或)。
基本性质3:
不等式两边都乘以(或除以)同一个 不等号的方向 ,即:若a (
◆◆◆
名师提醒
◆◆◆
(
1
)
运用不等式的基本性质解题时
,
要
注意
与等式基本性质的区别与联系,特别强调:在不等式两边都乘以或除以一个负数时,不等号的方向要
改变。
(
2
)任意两个实数比较大小关系:
①
;
②
;
③
。
)
知识点三、一元一次不等式及其解法
1.一元一次不等式的定义:
只含有一个未知数,并且未知数的次数是 且系数 的不等式叫一元一次不等式,其一般形式为 或 (a≠0,a,b为已知数)。
2.解一元一次不 等 式 的 步 骤:
解一元一次不 等 式 的 步 骤和 解一 元一次方程的步骤相同,即包含 、去括号、 、合并同类项、 等五个步骤。
(
◆◆◆
名师提醒
◆◆◆
解
一元一次不
等
式在最后一步系数化为
1
时,
要特别注意
不等号的方向是否要改变
。
)
知识点四、一元一次不等式组及其解法
1.一元一次不等式组的定义:
把几个含有相同未知数的 所组成的不等式组,叫做一元一次不等式组;
2.一元一次不等式组的解集:
一元一次不等式组中,几个不等式解集的 ,叫做这个一元一次不等式组的解集,一元一次不等式组的解集通常用数轴来确定。
3.一元一次不等式组的解法步骤:
先求出不等式组中各个不等式的 ,再求出他们的 部分,就得到不等式组的解集。
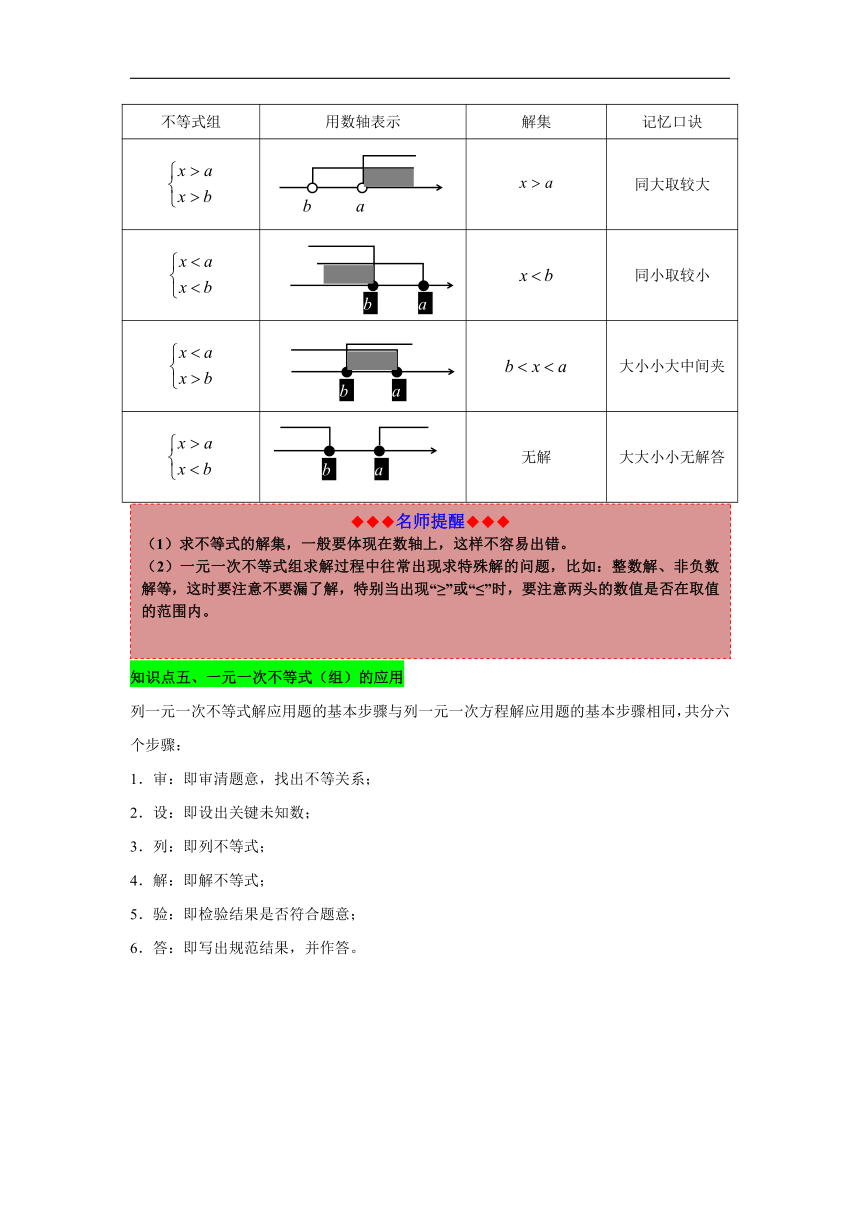
4.一元一次不等式组解集的确定方法,可以归纳为以下四种四种情况(设a>b):
不等式组 用数轴表示 解集 记忆口诀
(
a
b
) 同大取较大
(
a
b
) 同小取较小
(
a
b
) 大小小大中间夹
(
a
b
) 无解 大大小小无解答
(
◆◆◆
名师提醒
◆◆◆
(
1
)
求不等式的解集,一般要体现在数轴上,这样不容易出错。
(
2
)
一元一次不等式组求解过程中往常出现求特殊解的问题,比如:整数解、非负数解等,这时要注意不要漏了解,特别当出现
“≥”
或
“≤”
时
,
要注意两头的数值是否在取值的范围内
。
)
知识点五、一元一次不等式(组)的应用
列一元一次不等式解应用题的基本步骤与列一元一次方程解应用题的基本步骤相同,共分六个步骤:
1.审:即审清题意,找出不等关系;
2.设:即设出关键未知数;
3.列:即列不等式;
4.解:即解不等式;
5.验:即检验结果是否符合题意;
6.答:即写出规范结果,并作答。
(
◆◆◆
名师提醒
◆◆◆
表示不等关系的关键词与不等号对应如下:
)
★★★中考典例剖析★★★
考点一:不等式的性质
例1 (2018?广西)若m>n,则下列不等式正确的是( )
A.m-2<n-2 B. C.6m<6n D.-8m>-8n
【思路分析】将原不等式两边分别都减2、都除以4、都乘以6、都乘以-8,根据不等式得基本性质逐一判断即可得.
【解答】解:A、将m>n两边都减2得:m-2>n-2,此选项错误;
B、将m>n两边都除以4得:,此选项正确;
C、将m>n两边都乘以6得:6m>6n,此选项错误;
D、将m>n两边都乘以-8,得:-8m<-8n,此选项错误;
故选:B.
【点评】本题主要考查不等式的性质,解题的关键是掌握不等式的基本性质,尤其是性质不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变.
(
???
思维升华
???
应用不等式的性质应注意的问题是:在不等式的两边都乘以(或除以)同一个负数时,一定要改变不等号的方向;当不等式的两边要乘以(或除以)含有字母的数时,一定要对字母是否大于
0
进行分类讨论
。
)
跟踪训练
1.(2018?宿迁)若a<b,则下列结论不一定成立的是( )
A.a-1<b-1 B.2a<2b C. D.a2<b2
考点二:解一元一次不等式
例2 (2018?南京)如图,在数轴上,点A、B分别表示数1、-2x+3.
(1)求x的取值范围;
(2)数轴上表示数-x+2的点应落在 .
A.点A的左边?????????? B.线段AB上????????????? C.点B的右边
【思路分析】(1)根据数轴上的点表示的数右边的总比左边的大,可得不等式,根据解不等式,可得答案;
(2)根据不等式的性质,可得点在A点的右边,根据作差法,可得点在B点的左边.
【解答】解:(1)由数轴上的点表示的数右边的总比左边的大,得
-2x+3>1,
解得x<1;
(2)由x<1,得
-x>-1.
-x+2>-1+2,
解得-x+2>1.
数轴上表示数-x+2的点在A点的右边;
作差,得
-2x+3-(-x+2)=-x+1,
由x<1,得
-x>-1,
-x+1>0,
-2x+3-(-x+2)>0,
∴-2x+3>-x+2,
数轴上表示数-x+2的点在B点的左边.
故选:B.
【点评】本题考查了一元一次不等式,解(1)的关键是利用数轴上的点表示的数右边的总比左边的大得出不等式;解(2)的关键是利用不等式的性质。
(
●●●
触
雷
警示
●●●
解一元一次不等式的易错点
解一元一次不等式并用数轴表示解集时,最易出错的有以下三点:
(
1
)去分母时常数项漏项;
(
2
)两边同乘负数时,不等号方向忘记改变;
(
3
)用数轴表示解集时,忽略“实心圆点”与“空心圆圈”的区别。
)
跟踪训练
2.(2018?桂林)解不等式,并把它的解集在数轴上表示出来.
考点三:解一元一次不等式组
例3 (2018?永州)解不等式组,并把解集在数轴上表示出来.
【思路分析】分别解不等式组的两个不等式,即可得到其公共部分,依据解集即可在数轴上表示出来.
【解答】解:,
解不等式①,可得
x<3,
解不等式②,可得
x>-1,
∴不等式组的解集为-1<x<3,
在数轴上表示出来为:
【点评】本题主要考查了解一元一次不等式组,解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.
例4(2018?娄底)已知:[x]表示不超过x的最大整数.例:[3.9]=3,[-1.8]=-2.令关于k的函数 (k是正整数).例: .则下列结论错误的是( )
A.f(1)=0 B.f(k+4)=f(k) C.f(k+1)≥f(k) D.f(k)=0或1
【思路分析】根据题意可以判断各个选项是否正确,从而可以解答本题.
【解答】解:,故选项A正确;
,故选项B正确;
C、当k=3时, ,而f(3)=1,故选项C错误;
D、当k=3+4n(n为自然数)时,f(k)=1,当k为其它的正整数时,f(k)=0,所以D选项的结论正确;
选:C.
【点评】本题考查解一元一次不等式组、函数值,解答本题的关键是明确题意,可以判断各个选项中的结论是否成立.
(
???
思维升华
???
用数轴表示不等式的解集时,要注意
“
两定
”
:
一是定界点,一般在数轴上只标出原点和界点即可.定边界点时要注意,点是实心还是空心,若边界点含于解集为实心点,不含于解集即为空心点;
二是定方向,定方向的原则是:
“
小于向左,大于向右
”
。
)
跟踪训练
3.(2018?怀化)解不等式组 ,并把它的解集在数轴上表示出来.
4.(2018?聊城)若x为实数,则[x]表示不大于x的最大整数,例如[1.6]=1,[π]=3,[-2.82]=-3等.[x]+1是大于x的最小整数,对任意的实数x都满足不等式[x]≤x<[x]+1.①利用这个不等式①,求出满足[x]=2x-1的所有解,其所有解为 .
考点四:不等式(组)的整数解
例5 (2018?德阳)如果关于x的不等式组的整数解仅有x=2、x=3,那么适合这个不等式组的整数a、b组成的有序数对(a,b)共有( )
A.3个 B.4个 C.5个 D.6个
【思路分析】求出不等式组的解集,根据已知求出,求出2<a≤4、9≤b<12,即可得出答案.
【解答】解:解不等式2x-a≥0,得: ,
解不等式3x-b≤0,得:x≤,
∵不等式组的整数解仅有x=2、x=3,
则,
解得:2<a≤4、9≤b<12,
则a=3时,b=9、10、11;
当a=4时,b=9、10、11;
所以适合这个不等式组的整数a、b组成的有序数对(a,b)共有6个,
故选:D.
【点评】本题考查了解一元一次不等式组,不等式组的整数解,有序实数对的应用,解此题的根据是求出a、b的值.
(
???
思维升华
???
解决
“
一元一次不等式组的整数解问题
”
的关键在于
:
正确解得不等式组或不等式的解集,然后再根据题目中对于解集的限制得到下一步所需要的条件,再根据得到的条件进而求得不等式组的整数解
。
)
跟踪训练
5.(2018?泰安)不等式组有3个整数解,则a的取值范围是( )
A.-6≤a<-5 B.-6<a≤-5 C.-6<a<-5 D.-6≤a≤-5
考点五:确定不等式(组)中字母的取值范围
例6 (2018?呼和浩特)若不等式组的解集中的任意x,都能使不等式x-5>0成立,则a的取值范围是 .
【思路分析】先求出每个不等式的解集,再根据已知得出关于a的不等式,求出不等式的解集,再判断即可.
【解答】解:,
∵解不等式①得:x>-,
解不等式②得:x>-a+2,
∴不等式组的解集为x>-a+2,
∵不等式x-5>0的解集是x>5,
又∵不等式组的解集中的任意x,都能使不等式x-5>0成立,
∴-a+2≥5,
解得:a≤-6,
故答案为:a≤-6.
【点评】本题考查了解一元一次不等式和解一元一次不等式组,能得出关于a的不等式是解此题的关键.
跟踪训练
6.(2018?湖北)若关于x的一元一次不等式组的解集是x>3,则m的取值范围是( )
A.m>4 B.m≥4 C.m<4 D.m≤4
考点六:一元一次不等式(组)的应用
例7 (2018?赤峰)小明同学三次到某超市购买A、B两种商品,其中仅有一次是有折扣的,购买数量及消费金额如下表:
类别
次数 购买A商品数量(件) 购买B商品数量(件) 消费金额(元)
第一次 4 5 320
第二次 2 6 300
第三次 5 7 258
解答下列问题:
(1)第 次购买有折扣;
(2)求A、B两种商品的原价;
(3)若购买A、B两种商品的折扣数相同,求折扣数;
(4)小明同学再次购买A、B两种商品共10件,在(3)中折扣数的前提下,消费金额不超过200元,求至少购买A商品多少件.
【思路分析】(1)由第三次购买的A、B两种商品均比头两次多,总价反而少,可得出第三次购物有折扣;
(2)设A商品的原价为x元/件,B商品的原价为y元/件,根据总价=单价×数量结合前两次购物的数量及总价,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(3)设折扣数为z,根据总价=单价×数量,即可得出关于z的一元一次方程,解之即可得出结论;
(4)设购买A商品m件,则购买B商品(10-m)件,根据总价=单价×数量结合消费金额不超过200元,即可得出关于m的一元一次不等式,解之取其中的最小整数即可得出结论.
【解答】解:(1)观察表格数据,可知:第三次购买的A、B两种商品均比头两次多,总价反而少,
∴第三次购买有折扣.
故答案为:三.
(2)设A商品的原价为x元/件,B商品的原价为y元/件,
根据题意得: ,
解得: .
答:A商品的原价为30元/件,B商品的原价为40元/件.
(3)设折扣数为z,
根据题意得:,
解得:z=6.
答:折扣数为6.
(4)设购买A商品m件,则购买B商品(10-m)件,
根据题意得: ,
解得:m≥,
∵m为整数,
∴m的最小值为7.
答:至少购买A商品7件.
【点评】本题考查了一元一次方程的应用、二元一次方程组的应用以及一元一次不等式的应用,解题的关键是:(1)观察三次购物的数量及总价,找出哪次购物有折扣;(2)找准等量关系,正确列出二元一次方程组;(3)找准等量关系,正确列出一元一次方程;(4)根据各数量间的关系,正确列出一元一次不等式.
例8(2018?湘潭)湘潭市继2017年成功创建全国文明城市之后,又准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
【思路分析】(1)根据“购买2个温馨提示牌和3个垃圾箱共需550元”,建立方程求解即可得出结论;
(2)根据“费用不超过10000元和至少需要安放48个垃圾箱”,建立不等式即可得出结论.
【解答】解:(1)设温馨提示牌的单价为x元,则垃圾箱的单价为3x元,
根据题意得,2x+3×3x=550,
∴x=50,
经检验,符合题意,
∴3x=150元,
即:温馨提示牌和垃圾箱的单价各是50元和150元;
(2)设购买温馨提示牌y个(y为正整数),则垃圾箱为(100-y)个,
根据题意得,意, ,
∴50≤y≤52,
∵y为正整数,
∴y为50,51,52,共3种方案;
即:温馨提示牌50个,垃圾箱50个;温馨提示牌51个,垃圾箱49个;温馨提示牌52个,垃圾箱48个,
根据题意,费用为50y+150(100-y)=-100y+15000,
当y=52时,所需资金最少,最少是9800元.
【点评】此题主要考查了一元一次不等式组,一元一次方程的应用,正确找出相等关系是解本题的关键.
(
???
思维升华
???
运用不等式解决实际问题时,关键是分析问题中的数量关系,要注意抓住问题中的关键字,如“至少”、“不低于”、“不超过”、“不少于”等,找出不等关系,从而列出不等式求解。
)
【跟踪训练】
7.(2018?昆明)(列方程(组)及不等式解应用题)
水是人类生命之源.为了鼓励居民节约用水,相关部门实行居民生活用水阶梯式计量水价政策.若居民每户每月用水量不超过10立方米,每立方米按现行居民生活用水水价收费(现行居民生活用水水价=基本水价+污水处理费);若每户每月用水量超过10立方米,则超过部分每立方米在基本水价基础上加价100%,每立方米污水处理费不变.甲用户4月份用水8立方米,缴水费27.6元;乙用户4月份用水12立方米,缴水费46.3元.(注:污水处理的立方数=实际生活用水的立方数)。
(1)求每立方米的基本水价和每立方米的污水处理费各是多少元?
(2)如果某用户7月份生活用水水费计划不超过64元,该用户7月份最多可用水多少立方米?
8.(2018?济宁)“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 清理养鱼网箱人数/人 清理捕鱼网箱人数/人 总支出/元
A 15 9 57000
B 10 16 68000
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
(
?
??
感悟中考
?
??
分析
课程标准
和近五年的中考试题,可以发现中考命题主要集中在:实数的相反数、绝对值、倒数、科学记数法,题型一般为选择题和填空题,通过近五年考题的规律,
可以预测未来中考试题中
,实数的概念、科学记数法仍会作为重点进行考查。
)
★★★真题达标演练★★★
一、选择题
1.(2017?株洲)已知实数a,b满足a+1>b+1,则下列选项错误的为( )
A.a>b B.a+2>b+2 C.-a<-b D.2a>3b
2.(2018?长春)不等式3x-6≥0的解集在数轴上表示正确的是( )
A. B.
C. D.
3.(2018?株洲)下列哪个选项中的不等式与不等式5x>8+2x组成的不等式组的解集为<x<5( )
A.x+5<0 B.2x>10 C.3x-15<0 D.-x-5>0
4.(2018?海南)下列四个不等式组中,解集在数轴上表示如图所示的是( )
A. B. C. D.
5.(2018?湘西州)不等式组 的解集在数轴上表示正确的是( )
A. B.
C. D.
6.(2018?长沙)不等式组 的解集在数轴上表示正确的是( )
A. B.
C.
D.
7.(2018?恩施州)关于x的不等式组 的解集为x>3,那么a的取值范围为( )
A.a>3 B.a<3 C.a≥3 D.a≤3
8.(2018?临沂)不等式组 的正整数解的个数是( )
A.5 B.4 C.3 D.2
二、填空题
9.(2018?安徽)不等式的解集是 .
10.(2018?黔西南州)不等式组 的解集是 .
11.(2018?贵阳)已知关于x的不等式组无解,则a的取值范围是 .
12.(2018?黑龙江)不等式组 有3个整数解,则a的取值范围是 .
13.(2018?包头)不等式组的非负整数解有 个.
14.(2018?山西)2018年国内航空公司规定:旅客乘机时,免费携带行李箱的长,宽,高三者之和不超过115cm.某厂家生产符合该规定的行李箱.已知行李箱的宽为20cm,长与高的比为8:11,则符合此规定的行李箱的高的最大值为 cm.
三、解答题
15.(2018?威海)解不等式组,并将解集在数轴上表示出来.
16.(2018?天津)解不等式组 ,请结合题意填空,完成本题的解答.
(I)解不等式①,得 ;
(l1)解不等式②,得 ;
(Ⅲ)把不等式①和②的解集在数轴上表示出来;
(Ⅳ)原不等式组的解集为 .
17.(2018?资阳)为了美化市容市貌,政府决定将城区旁边一块162亩的荒地改建为湿地公园,规划公园分为绿化区和休闲区两部分.
(1)若休闲区面积是绿化区面积的20%,求改建后的绿化区和休闲区各有多少亩?
(2)经预算,绿化区的改建费用平均每亩35000元,休闲区的改建费用平均每亩25000元,政府计划投入资金不超过550万元,那么绿化区的面积最多可以达到多少亩?
18.(2018?南通)小明购买A,B两种商品,每次购买同一种商品的单价相同,具体信息如下表:
次数 购买数量(件) 购买总费用(元)
A B
第一次 2 1 55
第二次 1 3 65
根据以上信息解答下列问题:
(1)求A,B两种商品的单价;
(2)若第三次购买这两种商品共12件,且A种商品的数量不少于B种商品数量的2倍,请设计出最省钱的购买方案,并说明理由.
???详细参考答案???
把握命题趋势,提高复习效率,提升解题能力,打造中考高分!
2019版初中数学综合复习精品专题
第二章 方程与不等式
第十讲 一元一次不等式(组)
★★★核心知识回顾★★★
知识点一、不等式的基本概念
1.不等式:
用 不等号 连接起来的式子叫做不等式。
2.不等式的解:
使不等式成立的 未知数 的值,叫做不等式的解。
3.不等式的解集:
一个含有未知数的不等的解的 全体 叫做不等式的解集。
知识点二、不等式的基本性质:
基本性质1:
不等式两边都加上(或减去)同一个 数 或同一个 整式 不等号的方向 不变 ,即:若a基本性质2:
不等式两边都乘以(或除以)同一个 正数 不等号的方向 不变 ,即:若a0则a c < b c(或)。
基本性质3:
不等式两边都乘以(或除以)同一个 负数 不等号的方向 改变 ,即:若a知识点三、一元一次不等式及其解法
1.一元一次不等式的定义:
只含有一个未知数,并且未知数的次数是 1 且系数 不等于0 的不等式叫一元一次不等式,其一般形式为或(a≠0,a,b为已知数)。
2.解一元一次不 等 式 的 步 骤:
解一元一次不 等 式 的 步 骤和 解一 元一次方程的步骤相同,即包含 去分母 、去括号、 移项 、合并同类项、 化系数为1 等五个步骤。
知识点四、一元一次不等式组及其解法
1.一元一次不等式组的定义:
把几个含有相同未知数的 几个一元一次不等式 所组成的不等式组,叫做一元一次不等式组;
2.一元一次不等式组的解集:
一元一次不等式组中,几个不等式解集的 公共部分 ,叫做这个一元一次不等式组的解集,一元一次不等式组的解集通常用数轴来确定。
3.一元一次不等式组的解法步骤:
先求出不等式组中各个不等式的 解集 ,再求出他们的 公共 部分,就得到不等式组的解集。
4.一元一次不等式组解集的确定方法,可以归纳为以下四种四种情况(设a>b):
不等式组 用数轴表示 解集 记忆口诀
(
a
b
) 同大取较大
(
a
b
) 同小取较小
(
a
b
) 大小小大中间夹
(
a
b
) 无解 大大小小无解答
★★★中考典例剖析★★★
考点一:不等式的性质
跟踪训练
1.D
解:A、在不等式a<b的两边同时减去1,不等式仍成立,即a-1<b-1,故本选项错误;
B、在不等式a<b的两边同时乘以2,不等式仍成立,即2a<2b,故本选项错误;
C、在不等式a<b的两边同时乘以,不等号的方向改变,即,故本选项错误;
D、当a=-5,b=1时,不等式a2<b2不成立,故本选项正确;
故选:D.
考点二:解一元一次不等式
跟踪训练
2.解:去分母,得:5x-1<3x+3,
移项,得:5x-3x<3+1,
合并同类项,得:2x<4,
系数化为1,得:x<2,
将不等式的解集表示在数轴上如下:
考点三:解一元一次不等式组
跟踪训练
3.解:解①得:x≤4,
解②得:x>2,
故不等式组的解为:2<x≤4,
解集在数轴上表示为:
4.x=0.5或x=1
解:∵对任意的实数x都满足不等式[x]≤x<[x]+1,[x]=2x-1,
∴2x-1≤x<2x-1+1,
解得,0<x≤1,
∵2x-1是整数,
∴x=0.5或x=1,
故答案为:x=0.5或x=1.
考点四:不等式(组)的整数解
跟踪训练
5.B
解:不等式组,
由,解得:x>4,
由4(x-1)≤2(x-a),解得:x≤2-a,
故不等式组的解为:4<x≤2-a,
由关于x的不等式组有3个整数解,
解得:7≤2-a<8,
解得:-6<a≤-5.
故选:B.
考点五:确定不等式(组)中字母的取值范围
跟踪训练
6.D
解:,
∵解不等式①得:x>3,
解不等式②得:x>m-1,
又∵关于x的一元一次不等式组的解集是x>3,
∴m-1≤3,
解得:m≤4,
故选:D.
考点六:一元一次不等式(组)的应用
【跟踪训练】
7.解:(1)设每立方米的基本水价是x元,每立方米的污水处理费是y元
,
解得: ,
答:每立方米的基本水价是2.45元,每立方米的污水处理费是1元.
(2)设该用户7月份可用水t立方米(t>10),
10×2.45+(t-10)×4.9+t≤64,
解得:t≤15,
答:如果某用户7月份生活用水水费计划不超过64元,该用户7月份最多可用水15立方米
8.解:(1)设清理养鱼网箱的人均费用为x元,清理捕鱼网箱的人均费用为y元,
根据题意,得: ,
解得: ,
答:清理养鱼网箱的人均费用为2000元,清理捕鱼网箱的人均费用为3000元;
(2)设m人清理养鱼网箱,则(40-m)人清理捕鱼网箱,
根据题意,得: ,
解得:18≤m<20,
∵m为整数,
∴m=18或m=19,
则分配清理人员方案有两种:
方案一:18人清理养鱼网箱,22人清理捕鱼网箱;
方案二:19人清理养鱼网箱,21人清理捕鱼网箱.
★★★真题达标演练★★★
一、选择题
1.D
解:由不等式的性质得a>b,a+2>b+2,-a<-b.
故选:D.
2.B
解:3x-6≥0,
3x≥6,
x≥2,
在数轴上表示为:
,
故选:B.
3.C
解:5x>8+2x,
解得:x>,
根据大小小大中间找可得另一个不等式的解集一定是x<5,
故选:C.
D解:由解集在数轴上的表示可知,该不等式组为,
故选:D.
5.C
解:不等式组的解集在数轴上表示如下:
故选:C.
6.C
解:解不等式x+2>0,得:x>-2,
解不等式2x-4≤0,得:x≤2,
则不等式组的解集为-2<x≤2,
将解集表示在数轴上如下:
故选:C.
7.D
解:解不等式2(x-1)>4,得:x>3,
解不等式a-x<0,得:x>a,
∵不等式组的解集为x>3,
∴a≤3,
故选:D.
8.C
解:解不等式1-2x<3,得:x>-1,
解不等式,得:x≤3,
则不等式组的解集为-1<x≤3,
所以不等式组的正整数解有1、2、3这3个,
故选:C.
二、填空题
9.x>10
解:去分母,得:x-8>2,
移项,得:x>2+8,
合并同类项,得:x>10,
故答案为:x>10.
10.x<3
解:由(1)x<4,由(2)x<3,所以x<3.
11.a≥2
解:,
由①得:x≤2,
由②得:x>a,
∵不等式组无解,
∴a≥2,
故答案为:a≥2.
12.-2≤a<-1
解:解不等式x-a>0,得:x>a,
解不等式1-x>2x-5,得:x<2,
∵不等式组有3个整数解,
∴不等式组的整数解为-1、0、1,
则-2≤a<-1,
故答案为:-2≤a<-1.
13.4
解:解不等式2x+7>3(x+1),得:x<4,
解不等式,得:x≤8,
则不等式组的解集为x<4,
所以该不等式组的非负整数解为0、1、2、3这4个,
故答案为:4.
14.55
解:设长为8x,高为11x,
由题意,得:19x+20≤115,
解得:x≤5,
故行李箱的高的最大值为:11x=55,
答:行李箱的高的最大值为55厘米.
故答案为:55
三、解答题
15.解:解不等式①,得x>-4,
解不等式②,得x≤2,
把不等式①②的解集在数轴上表示如图:
,
原不等式组的解集为-4<x≤2.
16.解:,
(I)解不等式①,得x≥-2;
(Ⅱ)解不等式②,得x≤1;
(Ⅲ)把不等式①和②的解集在数轴上表示出来为:
(Ⅳ)原不等式组的解集为-2≤x≤1.
故答案为:x≥-2,x≤1,-2≤x≤1.
17.解:(1)设改建后的绿化区面积为x亩.
由题意:x+20%?x=162,
解得x=135,
162-135=27,
答:改建后的绿化区面积为135亩和休闲区面积有27亩.
(2)设绿化区的面积为m亩.
由题意:35000m+25000(162-m)≤5500000,
解得m≤145,
答:绿化区的面积最多可以达到145亩.
18.解:(1)设A种商品的单价为x元,B种商品的单价为y元,根据题意可得: ,
解得: ,
答:A种商品的单价为20元,B种商品的单价为15元;
(2)设第三次购买商品A种a件,则购买B种商品(12-a)件,根据题意可得:
a≥2(12-a),得:8≤a≤12,
∵m=20a+15(12-a)=5a+180,
∴当a=8时所花钱数最少,即购买A商品8件,B商品4件.
???教师用书???
把握命题趋势,提高复习效率,提升解题能力,打造中考高分!
2019版初中数学综合复习精品专题
第二章 方程与不等式
第十讲 一元一次不等式(组)
★★★核心知识回顾★★★
知识点一、不等式的基本概念
1.不等式:
用 不等号 连接起来的式子叫做不等式。
2.不等式的解:
使不等式成立的 未知数 的值,叫做不等式的解。
3.不等式的解集:
一个含有未知数的不等的解的 全体 叫做不等式的解集。
(
◆◆◆
名师提醒
◆◆◆
(
1
)常见的不等号有五种:“≠”,“>”,“<”,“≥”,“≤”;
(
2
)
不等式的解与解集是不同的两个概念,不等式的解是单独的未知数的值,而解集是一个范围的未知数的值组成的集合,一般由无数个解组成
;
(
3
)
不等式的解集一般可以在数轴上
直观的
表示出来
,具体方法是:
①先确定边界点,解集包含边界点,用实心圆点表示;不包含边界点的,用空心圆圈表示;
②再确定方向:大向右,小向左
。
)
知识点二、不等式的基本性质:
基本性质1:
不等式两边都加上(或减去)同一个 数 或同一个 整式 不等号的方向 不变 ,即:若a基本性质2:
不等式两边都乘以(或除以)同一个 正数 不等号的方向 不变 ,即:若a0则a c < b c(或)。
基本性质3:
不等式两边都乘以(或除以)同一个 负数 不等号的方向 改变 ,即:若a (
◆◆◆
名师提醒
◆◆◆
(
1
)
运用不等式的基本性质解题时
,
要
注意
与等式基本性质的区别与联系,特别强调:在不等式两边都乘以或除以一个负数时,不等号的方向要
改变。
(
2
)任意两个实数比较大小关系:
①
;
②
;
③
。
)
知识点三、一元一次不等式及其解法
1.一元一次不等式的定义:
只含有一个未知数,并且未知数的次数是 1 且系数 不等于0 的不等式叫一元一次不等式,其一般形式为或(a≠0,a,b为已知数)。
2.解一元一次不 等 式 的 步 骤:
解一元一次不 等 式 的 步 骤和 解一 元一次方程的步骤相同,即包含 去分母 、去括号、 移项 、合并同类项、 化系数为1 等五个步骤。
(
◆◆◆
名师提醒
◆◆◆
解
一元一次不
等
式在最后一步系数化为
1
时,
要特别注意
不等号的方向是否要改变
。
)
知识点四、一元一次不等式组及其解法
1.一元一次不等式组的定义:
把几个含有相同未知数的 几个一元一次不等式 所组成的不等式组,叫做一元一次不等式组;
2.一元一次不等式组的解集:
一元一次不等式组中,几个不等式解集的 公共部分 ,叫做这个一元一次不等式组的解集,一元一次不等式组的解集通常用数轴来确定。
3.一元一次不等式组的解法步骤:
先求出不等式组中各个不等式的 解集 ,再求出他们的 公共 部分,就得到不等式组的解集。
4.一元一次不等式组解集的确定方法,可以归纳为以下四种四种情况(设a>b):
不等式组 用数轴表示 解集 记忆口诀
(
a
b
) 同大取较大
(
a
b
) 同小取较小
(
a
b
) 大小小大中间夹
(
a
b
) 无解 大大小小无解答
(
◆◆◆
名师提醒
◆◆◆
(
1
)
求不等式的解集,一般要体现在数轴上,这样不容易出错。
(
2
)
一元一次不等式组求解过程中往常出现求特殊解的问题,比如:整数解、非负数解等,这时要注意不要漏了解,特别当出现
“≥”
或
“≤”
时
,
要注意两头的数值是否在取值的范围内
。
)
知识点五、一元一次不等式(组)的应用
列一元一次不等式解应用题的基本步骤与列一元一次方程解应用题的基本步骤相同,共分六个步骤:
1.审:即审清题意,找出不等关系;
2.设:即设出关键未知数;
3.列:即列不等式;
4.解:即解不等式;
5.验:即检验结果是否符合题意;
6.答:即写出规范结果,并作答。
(
◆◆◆
名师提醒
◆◆◆
表示不等关系的关键词与不等号对应如下:
)
★★★中考典例剖析★★★
考点一:不等式的性质
例1 (2018?广西)若m>n,则下列不等式正确的是( )
A.m-2<n-2 B. C.6m<6n D.-8m>-8n
【思路分析】将原不等式两边分别都减2、都除以4、都乘以6、都乘以-8,根据不等式得基本性质逐一判断即可得.
【解答】解:A、将m>n两边都减2得:m-2>n-2,此选项错误;
B、将m>n两边都除以4得:,此选项正确;
C、将m>n两边都乘以6得:6m>6n,此选项错误;
D、将m>n两边都乘以-8,得:-8m<-8n,此选项错误;
故选:B.
【点评】本题主要考查不等式的性质,解题的关键是掌握不等式的基本性质,尤其是性质不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变.
(
???
思维升华
???
应用不等式的性质应注意的问题是:在不等式的两边都乘以(或除以)同一个负数时,一定要改变不等号的方向;当不等式的两边要乘以(或除以)含有字母的数时,一定要对字母是否大于
0
进行分类讨论
。
)
跟踪训练
1.(2018?宿迁)若a<b,则下列结论不一定成立的是( )
A.a-1<b-1 B.2a<2b C. D.a2<b2
【思路分析】由不等式的性质进行计算并作出正确的判断.
【解答】解:A、在不等式a<b的两边同时减去1,不等式仍成立,即a-1<b-1,故本选项错误;
B、在不等式a<b的两边同时乘以2,不等式仍成立,即2a<2b,故本选项错误;
C、在不等式a<b的两边同时乘以,不等号的方向改变,即,故本选项错误;
D、当a=-5,b=1时,不等式a2<b2不成立,故本选项正确;
故选:D.
【点评】考查了不等式的性质.应用不等式的性质应注意的问题:在不等式的两边都乘以(或除以)同一个负数时,一定要改变不等号的方向;当不等式的两边要乘以(或除以)含有字母的数时,一定要对字母是否大于0进行分类讨论.
考点二:解一元一次不等式
例2 (2018?南京)如图,在数轴上,点A、B分别表示数1、-2x+3.
(1)求x的取值范围;
(2)数轴上表示数-x+2的点应落在 .
A.点A的左边?????????? B.线段AB上????????????? C.点B的右边
【思路分析】(1)根据数轴上的点表示的数右边的总比左边的大,可得不等式,根据解不等式,可得答案;
(2)根据不等式的性质,可得点在A点的右边,根据作差法,可得点在B点的左边.
【解答】解:(1)由数轴上的点表示的数右边的总比左边的大,得
-2x+3>1,
解得x<1;
(2)由x<1,得
-x>-1.
-x+2>-1+2,
解得-x+2>1.
数轴上表示数-x+2的点在A点的右边;
作差,得
-2x+3-(-x+2)=-x+1,
由x<1,得
-x>-1,
-x+1>0,
-2x+3-(-x+2)>0,
∴-2x+3>-x+2,
数轴上表示数-x+2的点在B点的左边.
故选:B.
【点评】本题考查了一元一次不等式,解(1)的关键是利用数轴上的点表示的数右边的总比左边的大得出不等式;解(2)的关键是利用不等式的性质。
(
●●●
触
雷
警示
●●●
解一元一次不等式的易错点
解一元一次不等式并用数轴表示解集时,最易出错的有以下三点:
(
1
)去分母时常数项漏项;
(
2
)两边同乘负数时,不等号方向忘记改变;
(
3
)用数轴表示解集时,忽略“实心圆点”与“空心圆圈”的区别。
)
跟踪训练
2.(2018?桂林)解不等式,并把它的解集在数轴上表示出来.
【思路分析】根据解一元一次不等式的步骤:①去分母;②去括号;③移项;④合并同类项;⑤化系数为1.依次计算可得.
【解答】解:去分母,得:5x-1<3x+3,
移项,得:5x-3x<3+1,
合并同类项,得:2x<4,
系数化为1,得:x<2,
将不等式的解集表示在数轴上如下:
【点评】本题主要考查解一元一次不等式,解题的关键是掌握解不等式的步骤:①去分母;②去括号;③移项;④合并同类项;⑤化系数为1.
考点三:解一元一次不等式组
例3 (2018?永州)解不等式组,并把解集在数轴上表示出来.
【思路分析】分别解不等式组的两个不等式,即可得到其公共部分,依据解集即可在数轴上表示出来.
【解答】解:,
解不等式①,可得
x<3,
解不等式②,可得
x>-1,
∴不等式组的解集为-1<x<3,
在数轴上表示出来为:
【点评】本题主要考查了解一元一次不等式组,解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.
例4(2018?娄底)已知:[x]表示不超过x的最大整数.例:[3.9]=3,[-1.8]=-2.令关于k的函数 (k是正整数).例: .则下列结论错误的是( )
A.f(1)=0 B.f(k+4)=f(k) C.f(k+1)≥f(k) D.f(k)=0或1
【思路分析】根据题意可以判断各个选项是否正确,从而可以解答本题.
【解答】解:,故选项A正确;
,故选项B正确;
C、当k=3时, ,而f(3)=1,故选项C错误;
D、当k=3+4n(n为自然数)时,f(k)=1,当k为其它的正整数时,f(k)=0,所以D选项的结论正确;
选:C.
【点评】本题考查解一元一次不等式组、函数值,解答本题的关键是明确题意,可以判断各个选项中的结论是否成立.
(
???
思维升华
???
用数轴表示不等式的解集时,要注意
“
两定
”
:
一是定界点,一般在数轴上只标出原点和界点即可.定边界点时要注意,点是实心还是空心,若边界点含于解集为实心点,不含于解集即为空心点;
二是定方向,定方向的原则是:
“
小于向左,大于向右
”
。
)
跟踪训练
3.(2018?怀化)解不等式组 ,并把它的解集在数轴上表示出来.
【思路分析】分别解两不等式,进而得出公共解集.
【解答】解:解①得:x≤4,
解②得:x>2,
故不等式组的解为:2<x≤4,
解集在数轴上表示为:
【点评】此题主要考查了解一元一次不等式组的解法,正确掌握基本解题思路是解题关键.
4.(2018?聊城)若x为实数,则[x]表示不大于x的最大整数,例如[1.6]=1,[π]=3,[-2.82]=-3等.[x]+1是大于x的最小整数,对任意的实数x都满足不等式[x]≤x<[x]+1.①利用这个不等式①,求出满足[x]=2x-1的所有解,其所有解为 .
【思路分析】根据题意可以列出相应的不等式,从而可以求得x的取值范围,本题得以解决.
【解答】解:∵对任意的实数x都满足不等式[x]≤x<[x]+1,[x]=2x-1,
∴2x-1≤x<2x-1+1,
解得,0<x≤1,
∵2x-1是整数,
∴x=0.5或x=1,
故答案为:x=0.5或x=1.
【点评】本题考查了解一元一次不等式组,解答本题的关键是明确题意,会解答一元一次不等式.
考点四:不等式(组)的整数解
例5 (2018?德阳)如果关于x的不等式组的整数解仅有x=2、x=3,那么适合这个不等式组的整数a、b组成的有序数对(a,b)共有( )
A.3个 B.4个 C.5个 D.6个
【思路分析】求出不等式组的解集,根据已知求出,求出2<a≤4、9≤b<12,即可得出答案.
【解答】解:解不等式2x-a≥0,得: ,
解不等式3x-b≤0,得:x≤,
∵不等式组的整数解仅有x=2、x=3,
则,
解得:2<a≤4、9≤b<12,
则a=3时,b=9、10、11;
当a=4时,b=9、10、11;
所以适合这个不等式组的整数a、b组成的有序数对(a,b)共有6个,
故选:D.
【点评】本题考查了解一元一次不等式组,不等式组的整数解,有序实数对的应用,解此题的根据是求出a、b的值.
(
???
思维升华
???
解决
“
一元一次不等式组的整数解问题
”
的关键在于
:
正确解得不等式组或不等式的解集,然后再根据题目中对于解集的限制得到下一步所需要的条件,再根据得到的条件进而求得不等式组的整数解
。
)
跟踪训练
5.(2018?泰安)不等式组有3个整数解,则a的取值范围是( )
A.-6≤a<-5 B.-6<a≤-5 C.-6<a<-5 D.-6≤a≤-5
【思路分析】根据解不等式组,可得不等式组的解,根据不等式组的解有3个整数解,可得答案.
【解答】解:不等式组,
由,解得:x>4,
由4(x-1)≤2(x-a),解得:x≤2-a,
故不等式组的解为:4<x≤2-a,
由关于x的不等式组有3个整数解,
解得:7≤2-a<8,
解得:-6<a≤-5.
故选:B.
【点评】本题考查了一元一次不等式组,利用不等式的解得出关于a的不等式是解题关键.
考点五:确定不等式(组)中字母的取值范围
例6 (2018?呼和浩特)若不等式组的解集中的任意x,都能使不等式x-5>0成立,则a的取值范围是 .
【思路分析】先求出每个不等式的解集,再根据已知得出关于a的不等式,求出不等式的解集,再判断即可.
【解答】解:,
∵解不等式①得:x>-,
解不等式②得:x>-a+2,
∴不等式组的解集为x>-a+2,
∵不等式x-5>0的解集是x>5,
又∵不等式组的解集中的任意x,都能使不等式x-5>0成立,
∴-a+2≥5,
解得:a≤-6,
故答案为:a≤-6.
【点评】本题考查了解一元一次不等式和解一元一次不等式组,能得出关于a的不等式是解此题的关键.
跟踪训练
6.(2018?湖北)若关于x的一元一次不等式组的解集是x>3,则m的取值范围是( )
A.m>4 B.m≥4 C.m<4 D.m≤4
【思路分析】先求出每个不等式的解集,再根据不等式组的解集和已知得出关于m的不等式,再求出解集即可.
【解答】解:,
∵解不等式①得:x>3,
解不等式②得:x>m-1,
又∵关于x的一元一次不等式组的解集是x>3,
∴m-1≤3,
解得:m≤4,
故选:D.
【点评】本题考查了解一元一次不等式组,能根据不等式的解集和已知得出关于m的不等式是解此题的关键.
考点六:一元一次不等式(组)的应用
例7 (2018?赤峰)小明同学三次到某超市购买A、B两种商品,其中仅有一次是有折扣的,购买数量及消费金额如下表:
类别
次数 购买A商品数量(件) 购买B商品数量(件) 消费金额(元)
第一次 4 5 320
第二次 2 6 300
第三次 5 7 258
解答下列问题:
(1)第 次购买有折扣;
(2)求A、B两种商品的原价;
(3)若购买A、B两种商品的折扣数相同,求折扣数;
(4)小明同学再次购买A、B两种商品共10件,在(3)中折扣数的前提下,消费金额不超过200元,求至少购买A商品多少件.
【思路分析】(1)由第三次购买的A、B两种商品均比头两次多,总价反而少,可得出第三次购物有折扣;
(2)设A商品的原价为x元/件,B商品的原价为y元/件,根据总价=单价×数量结合前两次购物的数量及总价,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(3)设折扣数为z,根据总价=单价×数量,即可得出关于z的一元一次方程,解之即可得出结论;
(4)设购买A商品m件,则购买B商品(10-m)件,根据总价=单价×数量结合消费金额不超过200元,即可得出关于m的一元一次不等式,解之取其中的最小整数即可得出结论.
【解答】解:(1)观察表格数据,可知:第三次购买的A、B两种商品均比头两次多,总价反而少,
∴第三次购买有折扣.
故答案为:三.
(2)设A商品的原价为x元/件,B商品的原价为y元/件,
根据题意得: ,
解得: .
答:A商品的原价为30元/件,B商品的原价为40元/件.
(3)设折扣数为z,
根据题意得:,
解得:z=6.
答:折扣数为6.
(4)设购买A商品m件,则购买B商品(10-m)件,
根据题意得: ,
解得:m≥,
∵m为整数,
∴m的最小值为7.
答:至少购买A商品7件.
【点评】本题考查了一元一次方程的应用、二元一次方程组的应用以及一元一次不等式的应用,解题的关键是:(1)观察三次购物的数量及总价,找出哪次购物有折扣;(2)找准等量关系,正确列出二元一次方程组;(3)找准等量关系,正确列出一元一次方程;(4)根据各数量间的关系,正确列出一元一次不等式.
例8(2018?湘潭)湘潭市继2017年成功创建全国文明城市之后,又准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
【思路分析】(1)根据“购买2个温馨提示牌和3个垃圾箱共需550元”,建立方程求解即可得出结论;
(2)根据“费用不超过10000元和至少需要安放48个垃圾箱”,建立不等式即可得出结论.
【解答】解:(1)设温馨提示牌的单价为x元,则垃圾箱的单价为3x元,
根据题意得,2x+3×3x=550,
∴x=50,
经检验,符合题意,
∴3x=150元,
即:温馨提示牌和垃圾箱的单价各是50元和150元;
(2)设购买温馨提示牌y个(y为正整数),则垃圾箱为(100-y)个,
根据题意得,意, ,
∴50≤y≤52,
∵y为正整数,
∴y为50,51,52,共3种方案;
即:温馨提示牌50个,垃圾箱50个;温馨提示牌51个,垃圾箱49个;温馨提示牌52个,垃圾箱48个,
根据题意,费用为50y+150(100-y)=-100y+15000,
当y=52时,所需资金最少,最少是9800元.
【点评】此题主要考查了一元一次不等式组,一元一次方程的应用,正确找出相等关系是解本题的关键.
(
???
思维升华
???
运用不等式解决实际问题时,关键是分析问题中的数量关系,要注意抓住问题中的关键字,如“至少”、“不低于”、“不超过”、“不少于”等,找出不等关系,从而列出不等式求解。
)
【跟踪训练】
7.(2018?昆明)(列方程(组)及不等式解应用题)
水是人类生命之源.为了鼓励居民节约用水,相关部门实行居民生活用水阶梯式计量水价政策.若居民每户每月用水量不超过10立方米,每立方米按现行居民生活用水水价收费(现行居民生活用水水价=基本水价+污水处理费);若每户每月用水量超过10立方米,则超过部分每立方米在基本水价基础上加价100%,每立方米污水处理费不变.甲用户4月份用水8立方米,缴水费27.6元;乙用户4月份用水12立方米,缴水费46.3元.(注:污水处理的立方数=实际生活用水的立方数)。
(1)求每立方米的基本水价和每立方米的污水处理费各是多少元?
(2)如果某用户7月份生活用水水费计划不超过64元,该用户7月份最多可用水多少立方米?
【思路分析】(1)设每立方米的基本水价是x元,每立方米的污水处理费是y元,然后根据等量关系即可列出方程求出答案.
(2)设该用户7月份可用水t立方米(t>10),根据题意列出不等式即可求出答案.
【解答】解:(1)设每立方米的基本水价是x元,每立方米的污水处理费是y元
,
解得: ,
答:每立方米的基本水价是2.45元,每立方米的污水处理费是1元.
(2)设该用户7月份可用水t立方米(t>10),
10×2.45+(t-10)×4.9+t≤64,
解得:t≤15,
答:如果某用户7月份生活用水水费计划不超过64元,该用户7月份最多可用水15立方米
【点评】本题考查学生的应用能力,解题的关键是根据题意列出方程和不等式,本题属于中等题型.
8.(2018?济宁)“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 清理养鱼网箱人数/人 清理捕鱼网箱人数/人 总支出/元
A 15 9 57000
B 10 16 68000
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
【思路分析】(1)设清理养鱼网箱的人均费用为x元,清理捕鱼网箱的人均费用为y元,根据A、B两村庄总支出列出关于x、y的方程组,解之可得;
(2)设m人清理养鱼网箱,则(40-m)人清理捕鱼网箱,根据“总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数”列不等式组求解可得.
【解答】解:(1)设清理养鱼网箱的人均费用为x元,清理捕鱼网箱的人均费用为y元,
根据题意,得: ,
解得: ,
答:清理养鱼网箱的人均费用为2000元,清理捕鱼网箱的人均费用为3000元;
(2)设m人清理养鱼网箱,则(40-m)人清理捕鱼网箱,
根据题意,得: ,
解得:18≤m<20,
∵m为整数,
∴m=18或m=19,
则分配清理人员方案有两种:
方案一:18人清理养鱼网箱,22人清理捕鱼网箱;
方案二:19人清理养鱼网箱,21人清理捕鱼网箱.
【点评】本题主要考查二元一次方程组和一元一次不等式组的应用,解题的关键是理解题意,找到题目蕴含的相等关系或不等关系,并据此列出方程或不等式组.
(
?
??
感悟中考
?
??
分析
课程标准
和近五年的中考试题,可以发现中考命题主要集中在:实数的相反数、绝对值、倒数、科学记数法,题型一般为选择题和填空题,通过近五年考题的规律,
可以预测未来中考试题中
,实数的概念、科学记数法仍会作为重点进行考查。
)
★★★真题达标演练★★★
一、选择题
1.(2017?株洲)已知实数a,b满足a+1>b+1,则下列选项错误的为( )
A.a>b B.a+2>b+2 C.-a<-b D.2a>3b
【思路分析】根据不等式的性质即可得到a>b,a+2>b+2,-a<-b.
【解答】解:由不等式的性质得a>b,a+2>b+2,-a<-b.
故选:D.
【点评】本题考查了不等式的性质,属于基础题.
2.(2018?长春)不等式3x-6≥0的解集在数轴上表示正确的是( )
A. B.
C. D.
【思路分析】先求出不等式的解集,再在数轴上表示出来即可.
【解答】解:3x-6≥0,
3x≥6,
x≥2,
在数轴上表示为:
,
故选:B.
【点评】本题考查了解一元一次不等式和在数轴上表示不等式的解集,能求出不等式的解集是解此题的关键.
3.(2018?株洲)下列哪个选项中的不等式与不等式5x>8+2x组成的不等式组的解集为<x<5( )
A.x+5<0 B.2x>10 C.3x-15<0 D.-x-5>0
【思路分析】首先计算出不等式5x>8+2x的解集,再根据不等式的解集确定方法:大小小大中间找可确定另一个不等式的解集,进而选出答案.
【解答】解:5x>8+2x,
解得:x>,
根据大小小大中间找可得另一个不等式的解集一定是x<5,
故选:C.
【点评】此题主要考查了不等式的解集,关键是正确理解不等式组解集的确定方法:大大取大,小小取小,大小小大中间找,大大小小找不着.
4.(2018?海南)下列四个不等式组中,解集在数轴上表示如图所示的是( )
A. B. C. D.
【思路分析】根据不等式组的表示方法,可得答案.
【解答】解:由解集在数轴上的表示可知,该不等式组为,
故选:D.
【点评】本题考查了在数轴上表示不等式的解集,利用不等式组的解集的表示方法:大小小大中间找是解题关键.
5.(2018?湘西州)不等式组 的解集在数轴上表示正确的是( )
A. B.
C. D.
【思路分析】先定界点,再定方向即可得.
【解答】解:不等式组的解集在数轴上表示如下:
故选:C.
【点评】本题考查了在数轴上表示不等式的解集,用数轴表示不等式的解集时,要注意“两定”:一是定界点,一般在数轴上只标出原点和界点即可.定边界点时要注意,点是实心还是空心,若边界点含于解集为实心点,不含于解集即为空心点;
二是定方向,定方向的原则是:“小于向左,大于向右”.
6.(2018?长沙)不等式组 的解集在数轴上表示正确的是( )
A. B.
C. D.
【思路分析】先求出各不等式的解集,再求出其公共解集即可.
【解答】解:解不等式x+2>0,得:x>-2,
解不等式2x-4≤0,得:x≤2,
则不等式组的解集为-2<x≤2,
将解集表示在数轴上如下:
故选:C.
【点评】本题主要考查解一元一次不等式组,要遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.
7.(2018?恩施州)关于x的不等式组 的解集为x>3,那么a的取值范围为( )
A.a>3 B.a<3 C.a≥3 D.a≤3
【思路分析】先解第一个不等式得到x>3,由于不等式组的解集为x>3,则利用同大取大可得到a的范围.
【解答】解:解不等式2(x-1)>4,得:x>3,
解不等式a-x<0,得:x>a,
∵不等式组的解集为x>3,
∴a≤3,
故选:D.
【点评】本题考查了解一元一次不等式组:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.
8.(2018?临沂)不等式组 的正整数解的个数是( )
A.5 B.4 C.3 D.2
【思路分析】先解不等式组得到-1<x≤3,再找出此范围内的正整数.
【解答】解:解不等式1-2x<3,得:x>-1,
解不等式,得:x≤3,
则不等式组的解集为-1<x≤3,
所以不等式组的正整数解有1、2、3这3个,
故选:C.
【点评】本题考查了一元一次不等式组的整数解:利用数轴确定不等式组的解(整数解).解决此类问题的关键在于正确解得不等式组或不等式的解集,然后再根据题目中对于解集的限制得到下一步所需要的条件,再根据得到的条件进而求得不等式组的整数解.
二、填空题
9.(2018?安徽)不等式的解集是 .
【思路分析】根据解一元一次不等式得基本步骤依次计算可得.
【解答】解:去分母,得:x-8>2,
移项,得:x>2+8,
合并同类项,得:x>10,
故答案为:x>10.
【点评】本题考查了解一元一次不等式:有分母先去分母,再去括号,然后进行移项,把含未知数的项移到不等式的左边,再进行合并同类项,最后把未知数的系数化为1可得到不等式的解集.
10.(2018?黔西南州)不等式组 的解集是 .
【思路分析】首先把两个不等式的解集分别解出来,再根据大大取大,小小取小,比大的小比小的大取中间,比大的大比小的小无解的原则,把不等式的解集用一个式子表示出来.
【解答】解:由(1)x<4,由(2)x<3,所以x<3.
【点评】本题考查不等式组的解法,一定要把每个不等式的解集正确解出来.
11.(2018?贵阳)已知关于x的不等式组无解,则a的取值范围是 .
【思路分析】先把a当作已知条件求出各不等式的解集,再根据不等式组无解求出a的取值范围即可.
【解答】解:,
由①得:x≤2,
由②得:x>a,
∵不等式组无解,
∴a≥2,
故答案为:a≥2.
【点评】此题主要考查了解一元一次不等式组,关键是掌握解集的规律:同大取大;同小取小;大小小大中间找;大大小小解没了.
12.(2018?黑龙江)不等式组 有3个整数解,则a的取值范围是 .
【思路分析】先解x的不等式组,然后根据整数解的个数确定a的取值范围.
【解答】解:解不等式x-a>0,得:x>a,
解不等式1-x>2x-5,得:x<2,
∵不等式组有3个整数解,
∴不等式组的整数解为-1、0、1,
则-2≤a<-1,
故答案为:-2≤a<-1.
【点评】本题考查了一元一次不等式组的整数解,难度适中,关键是根据整数解确定关于a的不等式组.
13.(2018?包头)不等式组的非负整数解有 个.
【思路分析】首先正确解不等式组,根据它的解集写出其非负整数解.
【解答】解:解不等式2x+7>3(x+1),得:x<4,
解不等式,得:x≤8,
则不等式组的解集为x<4,
所以该不等式组的非负整数解为0、1、2、3这4个,
故答案为:4.
【点评】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
14.(2018?山西)2018年国内航空公司规定:旅客乘机时,免费携带行李箱的长,宽,高三者之和不超过115cm.某厂家生产符合该规定的行李箱.已知行李箱的宽为20cm,长与高的比为8:11,则符合此规定的行李箱的高的最大值为 cm.
【思路分析】利用长与高的比为8:11,进而利用携带行李箱的长、宽、高三者之和不超过115cm得出不等式求出即可.
【解答】解:设长为8x,高为11x,
由题意,得:19x+20≤115,
解得:x≤5,
故行李箱的高的最大值为:11x=55,
答:行李箱的高的最大值为55厘米.
故答案为:55
【点评】此题主要考查了一元一次不等式的应用,根据题意得出正确不等关系是解题关键.
三、解答题
15.(2018?威海)解不等式组,并将解集在数轴上表示出来.
【思路分析】根据解一元一次不等式组的步骤,大小小大中间找,可得答案
【解答】解:解不等式①,得x>-4,
解不等式②,得x≤2,
把不等式①②的解集在数轴上表示如图:
,
原不等式组的解集为-4<x≤2.
【点评】本题考查了解一元一次不等式组,利用不等式组的解集的表示方法是解题关键.
16.(2018?天津)解不等式组 ,请结合题意填空,完成本题的解答.
(I)解不等式①,得 ;
(l1)解不等式②,得 ;
(Ⅲ)把不等式①和②的解集在数轴上表示出来;
(Ⅳ)原不等式组的解集为 .
【思路分析】先求出不等式组中每一个不等式的解集,再求出它们的公共部分,然后把不等式的解集表示在数轴上即可.
【解答】解:,
(I)解不等式①,得x≥-2;
(Ⅱ)解不等式②,得x≤1;
(Ⅲ)把不等式①和②的解集在数轴上表示出来为:
(Ⅳ)原不等式组的解集为-2≤x≤1.
故答案为:x≥-2,x≤1,-2≤x≤1.
【点评】此题考查了解一元一次不等式,其步骤为:去分母,去括号,移项合并,将未知数系数化为1,求出解集.
17.(2018?资阳)为了美化市容市貌,政府决定将城区旁边一块162亩的荒地改建为湿地公园,规划公园分为绿化区和休闲区两部分.
(1)若休闲区面积是绿化区面积的20%,求改建后的绿化区和休闲区各有多少亩?
(2)经预算,绿化区的改建费用平均每亩35000元,休闲区的改建费用平均每亩25000元,政府计划投入资金不超过550万元,那么绿化区的面积最多可以达到多少亩?
【思路分析】(1)设改建后的绿化区面积为x亩.根据总面积为162构建方程即可解决问题;
(2)设绿化区的面积为m亩.根据投入资金不超过550万元,根据不等式即可解决问题;
【解答】解:(1)设改建后的绿化区面积为x亩.
由题意:x+20%?x=162,
解得x=135,
162-135=27,
答:改建后的绿化区面积为135亩和休闲区面积有27亩.
(2)设绿化区的面积为m亩.
由题意:35000m+25000(162-m)≤5500000,
解得m≤145,
答:绿化区的面积最多可以达到145亩.
【点评】本题考查一元一次方程的应用,一元一次不等式的应用等知识,解题的关键是学会设未知数,寻找等量关系,构建方程或不等式解决问题.
18.(2018?南通)小明购买A,B两种商品,每次购买同一种商品的单价相同,具体信息如下表:
次数 购买数量(件) 购买总费用(元)
A B
第一次 2 1 55
第二次 1 3 65
根据以上信息解答下列问题:
(1)求A,B两种商品的单价;
(2)若第三次购买这两种商品共12件,且A种商品的数量不少于B种商品数量的2倍,请设计出最省钱的购买方案,并说明理由.
【思路分析】(1)根据表格中数据进而得出等式组成方程组求出答案;
(2)利用A种商品的数量不少于B种商品数量的2倍,得出商品数量的取值范围,进而求出答案.
【解答】解:(1)设A种商品的单价为x元,B种商品的单价为y元,根据题意可得: ,
解得: ,
答:A种商品的单价为20元,B种商品的单价为15元;
(2)设第三次购买商品A种a件,则购买B种商品(12-a)件,根据题意可得:
a≥2(12-a),
得:8≤a≤12,
∵m=20a+15(12-a)=5a+180,
∴当a=8时所花钱数最少,即购买A商品8件,B商品4件.
【点评】此题主要考查了二元一次方程组的应用以及一元一次不等式的应用,正确得出等量关系是解题关键.
把握命题趋势,提高复习效率,提升解题能力,打造中考高分!
2019版初中数学综合复习精品专题
第二章 方程与不等式
第十讲 一元一次不等式(组)
★★★核心知识回顾★★★
知识点一、不等式的基本概念
1.不等式:
用 连接起来的式子叫做不等式。
2.不等式的解:
使不等式成立的 的值,叫做不等式的解。
3.不等式的解集:
一个含有未知数的不等的解的 叫做不等式的解集。
(
◆◆◆
名师提醒
◆◆◆
(
1
)常见的不等号有五种:“≠”,“>”,“<”,“≥”,“≤”;
(
2
)
不等式的解与解集是不同的两个概念,不等式的解是单独的未知数的值,而解集是一个范围的未知数的值组成的集合,一般由无数个解组成
;
(
3
)
不等式的解集一般可以在数轴上
直观的
表示出来
,具体方法是:
①先确定边界点,解集包含边界点,用实心圆点表示;不包含边界点的,用空心圆圈表示;
②再确定方向:大向右,小向左
。
)
知识点二、不等式的基本性质:
基本性质1:
不等式两边都加上(或减去)同一个 或同一个 不等号的方向 ,即:若a
不等式两边都乘以(或除以)同一个 不等号的方向 ,即:若a
基本性质3:
不等式两边都乘以(或除以)同一个 不等号的方向 ,即:若a (
◆◆◆
名师提醒
◆◆◆
(
1
)
运用不等式的基本性质解题时
,
要
注意
与等式基本性质的区别与联系,特别强调:在不等式两边都乘以或除以一个负数时,不等号的方向要
改变。
(
2
)任意两个实数比较大小关系:
①
;
②
;
③
。
)
知识点三、一元一次不等式及其解法
1.一元一次不等式的定义:
只含有一个未知数,并且未知数的次数是 且系数 的不等式叫一元一次不等式,其一般形式为 或 (a≠0,a,b为已知数)。
2.解一元一次不 等 式 的 步 骤:
解一元一次不 等 式 的 步 骤和 解一 元一次方程的步骤相同,即包含 、去括号、 、合并同类项、 等五个步骤。
(
◆◆◆
名师提醒
◆◆◆
解
一元一次不
等
式在最后一步系数化为
1
时,
要特别注意
不等号的方向是否要改变
。
)
知识点四、一元一次不等式组及其解法
1.一元一次不等式组的定义:
把几个含有相同未知数的 所组成的不等式组,叫做一元一次不等式组;
2.一元一次不等式组的解集:
一元一次不等式组中,几个不等式解集的 ,叫做这个一元一次不等式组的解集,一元一次不等式组的解集通常用数轴来确定。
3.一元一次不等式组的解法步骤:
先求出不等式组中各个不等式的 ,再求出他们的 部分,就得到不等式组的解集。
4.一元一次不等式组解集的确定方法,可以归纳为以下四种四种情况(设a>b):
不等式组 用数轴表示 解集 记忆口诀
(
a
b
) 同大取较大
(
a
b
) 同小取较小
(
a
b
) 大小小大中间夹
(
a
b
) 无解 大大小小无解答
(
◆◆◆
名师提醒
◆◆◆
(
1
)
求不等式的解集,一般要体现在数轴上,这样不容易出错。
(
2
)
一元一次不等式组求解过程中往常出现求特殊解的问题,比如:整数解、非负数解等,这时要注意不要漏了解,特别当出现
“≥”
或
“≤”
时
,
要注意两头的数值是否在取值的范围内
。
)
知识点五、一元一次不等式(组)的应用
列一元一次不等式解应用题的基本步骤与列一元一次方程解应用题的基本步骤相同,共分六个步骤:
1.审:即审清题意,找出不等关系;
2.设:即设出关键未知数;
3.列:即列不等式;
4.解:即解不等式;
5.验:即检验结果是否符合题意;
6.答:即写出规范结果,并作答。
(
◆◆◆
名师提醒
◆◆◆
表示不等关系的关键词与不等号对应如下:
)
★★★中考典例剖析★★★
考点一:不等式的性质
例1 (2018?广西)若m>n,则下列不等式正确的是( )
A.m-2<n-2 B. C.6m<6n D.-8m>-8n
【思路分析】将原不等式两边分别都减2、都除以4、都乘以6、都乘以-8,根据不等式得基本性质逐一判断即可得.
【解答】解:A、将m>n两边都减2得:m-2>n-2,此选项错误;
B、将m>n两边都除以4得:,此选项正确;
C、将m>n两边都乘以6得:6m>6n,此选项错误;
D、将m>n两边都乘以-8,得:-8m<-8n,此选项错误;
故选:B.
【点评】本题主要考查不等式的性质,解题的关键是掌握不等式的基本性质,尤其是性质不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变.
(
???
思维升华
???
应用不等式的性质应注意的问题是:在不等式的两边都乘以(或除以)同一个负数时,一定要改变不等号的方向;当不等式的两边要乘以(或除以)含有字母的数时,一定要对字母是否大于
0
进行分类讨论
。
)
跟踪训练
1.(2018?宿迁)若a<b,则下列结论不一定成立的是( )
A.a-1<b-1 B.2a<2b C. D.a2<b2
考点二:解一元一次不等式
例2 (2018?南京)如图,在数轴上,点A、B分别表示数1、-2x+3.
(1)求x的取值范围;
(2)数轴上表示数-x+2的点应落在 .
A.点A的左边?????????? B.线段AB上????????????? C.点B的右边
【思路分析】(1)根据数轴上的点表示的数右边的总比左边的大,可得不等式,根据解不等式,可得答案;
(2)根据不等式的性质,可得点在A点的右边,根据作差法,可得点在B点的左边.
【解答】解:(1)由数轴上的点表示的数右边的总比左边的大,得
-2x+3>1,
解得x<1;
(2)由x<1,得
-x>-1.
-x+2>-1+2,
解得-x+2>1.
数轴上表示数-x+2的点在A点的右边;
作差,得
-2x+3-(-x+2)=-x+1,
由x<1,得
-x>-1,
-x+1>0,
-2x+3-(-x+2)>0,
∴-2x+3>-x+2,
数轴上表示数-x+2的点在B点的左边.
故选:B.
【点评】本题考查了一元一次不等式,解(1)的关键是利用数轴上的点表示的数右边的总比左边的大得出不等式;解(2)的关键是利用不等式的性质。
(
●●●
触
雷
警示
●●●
解一元一次不等式的易错点
解一元一次不等式并用数轴表示解集时,最易出错的有以下三点:
(
1
)去分母时常数项漏项;
(
2
)两边同乘负数时,不等号方向忘记改变;
(
3
)用数轴表示解集时,忽略“实心圆点”与“空心圆圈”的区别。
)
跟踪训练
2.(2018?桂林)解不等式,并把它的解集在数轴上表示出来.
考点三:解一元一次不等式组
例3 (2018?永州)解不等式组,并把解集在数轴上表示出来.
【思路分析】分别解不等式组的两个不等式,即可得到其公共部分,依据解集即可在数轴上表示出来.
【解答】解:,
解不等式①,可得
x<3,
解不等式②,可得
x>-1,
∴不等式组的解集为-1<x<3,
在数轴上表示出来为:
【点评】本题主要考查了解一元一次不等式组,解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.
例4(2018?娄底)已知:[x]表示不超过x的最大整数.例:[3.9]=3,[-1.8]=-2.令关于k的函数 (k是正整数).例: .则下列结论错误的是( )
A.f(1)=0 B.f(k+4)=f(k) C.f(k+1)≥f(k) D.f(k)=0或1
【思路分析】根据题意可以判断各个选项是否正确,从而可以解答本题.
【解答】解:,故选项A正确;
,故选项B正确;
C、当k=3时, ,而f(3)=1,故选项C错误;
D、当k=3+4n(n为自然数)时,f(k)=1,当k为其它的正整数时,f(k)=0,所以D选项的结论正确;
选:C.
【点评】本题考查解一元一次不等式组、函数值,解答本题的关键是明确题意,可以判断各个选项中的结论是否成立.
(
???
思维升华
???
用数轴表示不等式的解集时,要注意
“
两定
”
:
一是定界点,一般在数轴上只标出原点和界点即可.定边界点时要注意,点是实心还是空心,若边界点含于解集为实心点,不含于解集即为空心点;
二是定方向,定方向的原则是:
“
小于向左,大于向右
”
。
)
跟踪训练
3.(2018?怀化)解不等式组 ,并把它的解集在数轴上表示出来.
4.(2018?聊城)若x为实数,则[x]表示不大于x的最大整数,例如[1.6]=1,[π]=3,[-2.82]=-3等.[x]+1是大于x的最小整数,对任意的实数x都满足不等式[x]≤x<[x]+1.①利用这个不等式①,求出满足[x]=2x-1的所有解,其所有解为 .
考点四:不等式(组)的整数解
例5 (2018?德阳)如果关于x的不等式组的整数解仅有x=2、x=3,那么适合这个不等式组的整数a、b组成的有序数对(a,b)共有( )
A.3个 B.4个 C.5个 D.6个
【思路分析】求出不等式组的解集,根据已知求出,求出2<a≤4、9≤b<12,即可得出答案.
【解答】解:解不等式2x-a≥0,得: ,
解不等式3x-b≤0,得:x≤,
∵不等式组的整数解仅有x=2、x=3,
则,
解得:2<a≤4、9≤b<12,
则a=3时,b=9、10、11;
当a=4时,b=9、10、11;
所以适合这个不等式组的整数a、b组成的有序数对(a,b)共有6个,
故选:D.
【点评】本题考查了解一元一次不等式组,不等式组的整数解,有序实数对的应用,解此题的根据是求出a、b的值.
(
???
思维升华
???
解决
“
一元一次不等式组的整数解问题
”
的关键在于
:
正确解得不等式组或不等式的解集,然后再根据题目中对于解集的限制得到下一步所需要的条件,再根据得到的条件进而求得不等式组的整数解
。
)
跟踪训练
5.(2018?泰安)不等式组有3个整数解,则a的取值范围是( )
A.-6≤a<-5 B.-6<a≤-5 C.-6<a<-5 D.-6≤a≤-5
考点五:确定不等式(组)中字母的取值范围
例6 (2018?呼和浩特)若不等式组的解集中的任意x,都能使不等式x-5>0成立,则a的取值范围是 .
【思路分析】先求出每个不等式的解集,再根据已知得出关于a的不等式,求出不等式的解集,再判断即可.
【解答】解:,
∵解不等式①得:x>-,
解不等式②得:x>-a+2,
∴不等式组的解集为x>-a+2,
∵不等式x-5>0的解集是x>5,
又∵不等式组的解集中的任意x,都能使不等式x-5>0成立,
∴-a+2≥5,
解得:a≤-6,
故答案为:a≤-6.
【点评】本题考查了解一元一次不等式和解一元一次不等式组,能得出关于a的不等式是解此题的关键.
跟踪训练
6.(2018?湖北)若关于x的一元一次不等式组的解集是x>3,则m的取值范围是( )
A.m>4 B.m≥4 C.m<4 D.m≤4
考点六:一元一次不等式(组)的应用
例7 (2018?赤峰)小明同学三次到某超市购买A、B两种商品,其中仅有一次是有折扣的,购买数量及消费金额如下表:
类别
次数 购买A商品数量(件) 购买B商品数量(件) 消费金额(元)
第一次 4 5 320
第二次 2 6 300
第三次 5 7 258
解答下列问题:
(1)第 次购买有折扣;
(2)求A、B两种商品的原价;
(3)若购买A、B两种商品的折扣数相同,求折扣数;
(4)小明同学再次购买A、B两种商品共10件,在(3)中折扣数的前提下,消费金额不超过200元,求至少购买A商品多少件.
【思路分析】(1)由第三次购买的A、B两种商品均比头两次多,总价反而少,可得出第三次购物有折扣;
(2)设A商品的原价为x元/件,B商品的原价为y元/件,根据总价=单价×数量结合前两次购物的数量及总价,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(3)设折扣数为z,根据总价=单价×数量,即可得出关于z的一元一次方程,解之即可得出结论;
(4)设购买A商品m件,则购买B商品(10-m)件,根据总价=单价×数量结合消费金额不超过200元,即可得出关于m的一元一次不等式,解之取其中的最小整数即可得出结论.
【解答】解:(1)观察表格数据,可知:第三次购买的A、B两种商品均比头两次多,总价反而少,
∴第三次购买有折扣.
故答案为:三.
(2)设A商品的原价为x元/件,B商品的原价为y元/件,
根据题意得: ,
解得: .
答:A商品的原价为30元/件,B商品的原价为40元/件.
(3)设折扣数为z,
根据题意得:,
解得:z=6.
答:折扣数为6.
(4)设购买A商品m件,则购买B商品(10-m)件,
根据题意得: ,
解得:m≥,
∵m为整数,
∴m的最小值为7.
答:至少购买A商品7件.
【点评】本题考查了一元一次方程的应用、二元一次方程组的应用以及一元一次不等式的应用,解题的关键是:(1)观察三次购物的数量及总价,找出哪次购物有折扣;(2)找准等量关系,正确列出二元一次方程组;(3)找准等量关系,正确列出一元一次方程;(4)根据各数量间的关系,正确列出一元一次不等式.
例8(2018?湘潭)湘潭市继2017年成功创建全国文明城市之后,又准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
【思路分析】(1)根据“购买2个温馨提示牌和3个垃圾箱共需550元”,建立方程求解即可得出结论;
(2)根据“费用不超过10000元和至少需要安放48个垃圾箱”,建立不等式即可得出结论.
【解答】解:(1)设温馨提示牌的单价为x元,则垃圾箱的单价为3x元,
根据题意得,2x+3×3x=550,
∴x=50,
经检验,符合题意,
∴3x=150元,
即:温馨提示牌和垃圾箱的单价各是50元和150元;
(2)设购买温馨提示牌y个(y为正整数),则垃圾箱为(100-y)个,
根据题意得,意, ,
∴50≤y≤52,
∵y为正整数,
∴y为50,51,52,共3种方案;
即:温馨提示牌50个,垃圾箱50个;温馨提示牌51个,垃圾箱49个;温馨提示牌52个,垃圾箱48个,
根据题意,费用为50y+150(100-y)=-100y+15000,
当y=52时,所需资金最少,最少是9800元.
【点评】此题主要考查了一元一次不等式组,一元一次方程的应用,正确找出相等关系是解本题的关键.
(
???
思维升华
???
运用不等式解决实际问题时,关键是分析问题中的数量关系,要注意抓住问题中的关键字,如“至少”、“不低于”、“不超过”、“不少于”等,找出不等关系,从而列出不等式求解。
)
【跟踪训练】
7.(2018?昆明)(列方程(组)及不等式解应用题)
水是人类生命之源.为了鼓励居民节约用水,相关部门实行居民生活用水阶梯式计量水价政策.若居民每户每月用水量不超过10立方米,每立方米按现行居民生活用水水价收费(现行居民生活用水水价=基本水价+污水处理费);若每户每月用水量超过10立方米,则超过部分每立方米在基本水价基础上加价100%,每立方米污水处理费不变.甲用户4月份用水8立方米,缴水费27.6元;乙用户4月份用水12立方米,缴水费46.3元.(注:污水处理的立方数=实际生活用水的立方数)。
(1)求每立方米的基本水价和每立方米的污水处理费各是多少元?
(2)如果某用户7月份生活用水水费计划不超过64元,该用户7月份最多可用水多少立方米?
8.(2018?济宁)“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 清理养鱼网箱人数/人 清理捕鱼网箱人数/人 总支出/元
A 15 9 57000
B 10 16 68000
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
(
?
??
感悟中考
?
??
分析
课程标准
和近五年的中考试题,可以发现中考命题主要集中在:实数的相反数、绝对值、倒数、科学记数法,题型一般为选择题和填空题,通过近五年考题的规律,
可以预测未来中考试题中
,实数的概念、科学记数法仍会作为重点进行考查。
)
★★★真题达标演练★★★
一、选择题
1.(2017?株洲)已知实数a,b满足a+1>b+1,则下列选项错误的为( )
A.a>b B.a+2>b+2 C.-a<-b D.2a>3b
2.(2018?长春)不等式3x-6≥0的解集在数轴上表示正确的是( )
A. B.
C. D.
3.(2018?株洲)下列哪个选项中的不等式与不等式5x>8+2x组成的不等式组的解集为<x<5( )
A.x+5<0 B.2x>10 C.3x-15<0 D.-x-5>0
4.(2018?海南)下列四个不等式组中,解集在数轴上表示如图所示的是( )
A. B. C. D.
5.(2018?湘西州)不等式组 的解集在数轴上表示正确的是( )
A. B.
C. D.
6.(2018?长沙)不等式组 的解集在数轴上表示正确的是( )
A. B.
C.
D.
7.(2018?恩施州)关于x的不等式组 的解集为x>3,那么a的取值范围为( )
A.a>3 B.a<3 C.a≥3 D.a≤3
8.(2018?临沂)不等式组 的正整数解的个数是( )
A.5 B.4 C.3 D.2
二、填空题
9.(2018?安徽)不等式的解集是 .
10.(2018?黔西南州)不等式组 的解集是 .
11.(2018?贵阳)已知关于x的不等式组无解,则a的取值范围是 .
12.(2018?黑龙江)不等式组 有3个整数解,则a的取值范围是 .
13.(2018?包头)不等式组的非负整数解有 个.
14.(2018?山西)2018年国内航空公司规定:旅客乘机时,免费携带行李箱的长,宽,高三者之和不超过115cm.某厂家生产符合该规定的行李箱.已知行李箱的宽为20cm,长与高的比为8:11,则符合此规定的行李箱的高的最大值为 cm.
三、解答题
15.(2018?威海)解不等式组,并将解集在数轴上表示出来.
16.(2018?天津)解不等式组 ,请结合题意填空,完成本题的解答.
(I)解不等式①,得 ;
(l1)解不等式②,得 ;
(Ⅲ)把不等式①和②的解集在数轴上表示出来;
(Ⅳ)原不等式组的解集为 .
17.(2018?资阳)为了美化市容市貌,政府决定将城区旁边一块162亩的荒地改建为湿地公园,规划公园分为绿化区和休闲区两部分.
(1)若休闲区面积是绿化区面积的20%,求改建后的绿化区和休闲区各有多少亩?
(2)经预算,绿化区的改建费用平均每亩35000元,休闲区的改建费用平均每亩25000元,政府计划投入资金不超过550万元,那么绿化区的面积最多可以达到多少亩?
18.(2018?南通)小明购买A,B两种商品,每次购买同一种商品的单价相同,具体信息如下表:
次数 购买数量(件) 购买总费用(元)
A B
第一次 2 1 55
第二次 1 3 65
根据以上信息解答下列问题:
(1)求A,B两种商品的单价;
(2)若第三次购买这两种商品共12件,且A种商品的数量不少于B种商品数量的2倍,请设计出最省钱的购买方案,并说明理由.
???详细参考答案???
把握命题趋势,提高复习效率,提升解题能力,打造中考高分!
2019版初中数学综合复习精品专题
第二章 方程与不等式
第十讲 一元一次不等式(组)
★★★核心知识回顾★★★
知识点一、不等式的基本概念
1.不等式:
用 不等号 连接起来的式子叫做不等式。
2.不等式的解:
使不等式成立的 未知数 的值,叫做不等式的解。
3.不等式的解集:
一个含有未知数的不等的解的 全体 叫做不等式的解集。
知识点二、不等式的基本性质:
基本性质1:
不等式两边都加上(或减去)同一个 数 或同一个 整式 不等号的方向 不变 ,即:若a
不等式两边都乘以(或除以)同一个 正数 不等号的方向 不变 ,即:若a
基本性质3:
不等式两边都乘以(或除以)同一个 负数 不等号的方向 改变 ,即:若a知识点三、一元一次不等式及其解法
1.一元一次不等式的定义:
只含有一个未知数,并且未知数的次数是 1 且系数 不等于0 的不等式叫一元一次不等式,其一般形式为或(a≠0,a,b为已知数)。
2.解一元一次不 等 式 的 步 骤:
解一元一次不 等 式 的 步 骤和 解一 元一次方程的步骤相同,即包含 去分母 、去括号、 移项 、合并同类项、 化系数为1 等五个步骤。
知识点四、一元一次不等式组及其解法
1.一元一次不等式组的定义:
把几个含有相同未知数的 几个一元一次不等式 所组成的不等式组,叫做一元一次不等式组;
2.一元一次不等式组的解集:
一元一次不等式组中,几个不等式解集的 公共部分 ,叫做这个一元一次不等式组的解集,一元一次不等式组的解集通常用数轴来确定。
3.一元一次不等式组的解法步骤:
先求出不等式组中各个不等式的 解集 ,再求出他们的 公共 部分,就得到不等式组的解集。
4.一元一次不等式组解集的确定方法,可以归纳为以下四种四种情况(设a>b):
不等式组 用数轴表示 解集 记忆口诀
(
a
b
) 同大取较大
(
a
b
) 同小取较小
(
a
b
) 大小小大中间夹
(
a
b
) 无解 大大小小无解答
★★★中考典例剖析★★★
考点一:不等式的性质
跟踪训练
1.D
解:A、在不等式a<b的两边同时减去1,不等式仍成立,即a-1<b-1,故本选项错误;
B、在不等式a<b的两边同时乘以2,不等式仍成立,即2a<2b,故本选项错误;
C、在不等式a<b的两边同时乘以,不等号的方向改变,即,故本选项错误;
D、当a=-5,b=1时,不等式a2<b2不成立,故本选项正确;
故选:D.
考点二:解一元一次不等式
跟踪训练
2.解:去分母,得:5x-1<3x+3,
移项,得:5x-3x<3+1,
合并同类项,得:2x<4,
系数化为1,得:x<2,
将不等式的解集表示在数轴上如下:
考点三:解一元一次不等式组
跟踪训练
3.解:解①得:x≤4,
解②得:x>2,
故不等式组的解为:2<x≤4,
解集在数轴上表示为:
4.x=0.5或x=1
解:∵对任意的实数x都满足不等式[x]≤x<[x]+1,[x]=2x-1,
∴2x-1≤x<2x-1+1,
解得,0<x≤1,
∵2x-1是整数,
∴x=0.5或x=1,
故答案为:x=0.5或x=1.
考点四:不等式(组)的整数解
跟踪训练
5.B
解:不等式组,
由,解得:x>4,
由4(x-1)≤2(x-a),解得:x≤2-a,
故不等式组的解为:4<x≤2-a,
由关于x的不等式组有3个整数解,
解得:7≤2-a<8,
解得:-6<a≤-5.
故选:B.
考点五:确定不等式(组)中字母的取值范围
跟踪训练
6.D
解:,
∵解不等式①得:x>3,
解不等式②得:x>m-1,
又∵关于x的一元一次不等式组的解集是x>3,
∴m-1≤3,
解得:m≤4,
故选:D.
考点六:一元一次不等式(组)的应用
【跟踪训练】
7.解:(1)设每立方米的基本水价是x元,每立方米的污水处理费是y元
,
解得: ,
答:每立方米的基本水价是2.45元,每立方米的污水处理费是1元.
(2)设该用户7月份可用水t立方米(t>10),
10×2.45+(t-10)×4.9+t≤64,
解得:t≤15,
答:如果某用户7月份生活用水水费计划不超过64元,该用户7月份最多可用水15立方米
8.解:(1)设清理养鱼网箱的人均费用为x元,清理捕鱼网箱的人均费用为y元,
根据题意,得: ,
解得: ,
答:清理养鱼网箱的人均费用为2000元,清理捕鱼网箱的人均费用为3000元;
(2)设m人清理养鱼网箱,则(40-m)人清理捕鱼网箱,
根据题意,得: ,
解得:18≤m<20,
∵m为整数,
∴m=18或m=19,
则分配清理人员方案有两种:
方案一:18人清理养鱼网箱,22人清理捕鱼网箱;
方案二:19人清理养鱼网箱,21人清理捕鱼网箱.
★★★真题达标演练★★★
一、选择题
1.D
解:由不等式的性质得a>b,a+2>b+2,-a<-b.
故选:D.
2.B
解:3x-6≥0,
3x≥6,
x≥2,
在数轴上表示为:
,
故选:B.
3.C
解:5x>8+2x,
解得:x>,
根据大小小大中间找可得另一个不等式的解集一定是x<5,
故选:C.
D解:由解集在数轴上的表示可知,该不等式组为,
故选:D.
5.C
解:不等式组的解集在数轴上表示如下:
故选:C.
6.C
解:解不等式x+2>0,得:x>-2,
解不等式2x-4≤0,得:x≤2,
则不等式组的解集为-2<x≤2,
将解集表示在数轴上如下:
故选:C.
7.D
解:解不等式2(x-1)>4,得:x>3,
解不等式a-x<0,得:x>a,
∵不等式组的解集为x>3,
∴a≤3,
故选:D.
8.C
解:解不等式1-2x<3,得:x>-1,
解不等式,得:x≤3,
则不等式组的解集为-1<x≤3,
所以不等式组的正整数解有1、2、3这3个,
故选:C.
二、填空题
9.x>10
解:去分母,得:x-8>2,
移项,得:x>2+8,
合并同类项,得:x>10,
故答案为:x>10.
10.x<3
解:由(1)x<4,由(2)x<3,所以x<3.
11.a≥2
解:,
由①得:x≤2,
由②得:x>a,
∵不等式组无解,
∴a≥2,
故答案为:a≥2.
12.-2≤a<-1
解:解不等式x-a>0,得:x>a,
解不等式1-x>2x-5,得:x<2,
∵不等式组有3个整数解,
∴不等式组的整数解为-1、0、1,
则-2≤a<-1,
故答案为:-2≤a<-1.
13.4
解:解不等式2x+7>3(x+1),得:x<4,
解不等式,得:x≤8,
则不等式组的解集为x<4,
所以该不等式组的非负整数解为0、1、2、3这4个,
故答案为:4.
14.55
解:设长为8x,高为11x,
由题意,得:19x+20≤115,
解得:x≤5,
故行李箱的高的最大值为:11x=55,
答:行李箱的高的最大值为55厘米.
故答案为:55
三、解答题
15.解:解不等式①,得x>-4,
解不等式②,得x≤2,
把不等式①②的解集在数轴上表示如图:
,
原不等式组的解集为-4<x≤2.
16.解:,
(I)解不等式①,得x≥-2;
(Ⅱ)解不等式②,得x≤1;
(Ⅲ)把不等式①和②的解集在数轴上表示出来为:
(Ⅳ)原不等式组的解集为-2≤x≤1.
故答案为:x≥-2,x≤1,-2≤x≤1.
17.解:(1)设改建后的绿化区面积为x亩.
由题意:x+20%?x=162,
解得x=135,
162-135=27,
答:改建后的绿化区面积为135亩和休闲区面积有27亩.
(2)设绿化区的面积为m亩.
由题意:35000m+25000(162-m)≤5500000,
解得m≤145,
答:绿化区的面积最多可以达到145亩.
18.解:(1)设A种商品的单价为x元,B种商品的单价为y元,根据题意可得: ,
解得: ,
答:A种商品的单价为20元,B种商品的单价为15元;
(2)设第三次购买商品A种a件,则购买B种商品(12-a)件,根据题意可得:
a≥2(12-a),得:8≤a≤12,
∵m=20a+15(12-a)=5a+180,
∴当a=8时所花钱数最少,即购买A商品8件,B商品4件.
???教师用书???
把握命题趋势,提高复习效率,提升解题能力,打造中考高分!
2019版初中数学综合复习精品专题
第二章 方程与不等式
第十讲 一元一次不等式(组)
★★★核心知识回顾★★★
知识点一、不等式的基本概念
1.不等式:
用 不等号 连接起来的式子叫做不等式。
2.不等式的解:
使不等式成立的 未知数 的值,叫做不等式的解。
3.不等式的解集:
一个含有未知数的不等的解的 全体 叫做不等式的解集。
(
◆◆◆
名师提醒
◆◆◆
(
1
)常见的不等号有五种:“≠”,“>”,“<”,“≥”,“≤”;
(
2
)
不等式的解与解集是不同的两个概念,不等式的解是单独的未知数的值,而解集是一个范围的未知数的值组成的集合,一般由无数个解组成
;
(
3
)
不等式的解集一般可以在数轴上
直观的
表示出来
,具体方法是:
①先确定边界点,解集包含边界点,用实心圆点表示;不包含边界点的,用空心圆圈表示;
②再确定方向:大向右,小向左
。
)
知识点二、不等式的基本性质:
基本性质1:
不等式两边都加上(或减去)同一个 数 或同一个 整式 不等号的方向 不变 ,即:若a
不等式两边都乘以(或除以)同一个 正数 不等号的方向 不变 ,即:若a
基本性质3:
不等式两边都乘以(或除以)同一个 负数 不等号的方向 改变 ,即:若a (
◆◆◆
名师提醒
◆◆◆
(
1
)
运用不等式的基本性质解题时
,
要
注意
与等式基本性质的区别与联系,特别强调:在不等式两边都乘以或除以一个负数时,不等号的方向要
改变。
(
2
)任意两个实数比较大小关系:
①
;
②
;
③
。
)
知识点三、一元一次不等式及其解法
1.一元一次不等式的定义:
只含有一个未知数,并且未知数的次数是 1 且系数 不等于0 的不等式叫一元一次不等式,其一般形式为或(a≠0,a,b为已知数)。
2.解一元一次不 等 式 的 步 骤:
解一元一次不 等 式 的 步 骤和 解一 元一次方程的步骤相同,即包含 去分母 、去括号、 移项 、合并同类项、 化系数为1 等五个步骤。
(
◆◆◆
名师提醒
◆◆◆
解
一元一次不
等
式在最后一步系数化为
1
时,
要特别注意
不等号的方向是否要改变
。
)
知识点四、一元一次不等式组及其解法
1.一元一次不等式组的定义:
把几个含有相同未知数的 几个一元一次不等式 所组成的不等式组,叫做一元一次不等式组;
2.一元一次不等式组的解集:
一元一次不等式组中,几个不等式解集的 公共部分 ,叫做这个一元一次不等式组的解集,一元一次不等式组的解集通常用数轴来确定。
3.一元一次不等式组的解法步骤:
先求出不等式组中各个不等式的 解集 ,再求出他们的 公共 部分,就得到不等式组的解集。
4.一元一次不等式组解集的确定方法,可以归纳为以下四种四种情况(设a>b):
不等式组 用数轴表示 解集 记忆口诀
(
a
b
) 同大取较大
(
a
b
) 同小取较小
(
a
b
) 大小小大中间夹
(
a
b
) 无解 大大小小无解答
(
◆◆◆
名师提醒
◆◆◆
(
1
)
求不等式的解集,一般要体现在数轴上,这样不容易出错。
(
2
)
一元一次不等式组求解过程中往常出现求特殊解的问题,比如:整数解、非负数解等,这时要注意不要漏了解,特别当出现
“≥”
或
“≤”
时
,
要注意两头的数值是否在取值的范围内
。
)
知识点五、一元一次不等式(组)的应用
列一元一次不等式解应用题的基本步骤与列一元一次方程解应用题的基本步骤相同,共分六个步骤:
1.审:即审清题意,找出不等关系;
2.设:即设出关键未知数;
3.列:即列不等式;
4.解:即解不等式;
5.验:即检验结果是否符合题意;
6.答:即写出规范结果,并作答。
(
◆◆◆
名师提醒
◆◆◆
表示不等关系的关键词与不等号对应如下:
)
★★★中考典例剖析★★★
考点一:不等式的性质
例1 (2018?广西)若m>n,则下列不等式正确的是( )
A.m-2<n-2 B. C.6m<6n D.-8m>-8n
【思路分析】将原不等式两边分别都减2、都除以4、都乘以6、都乘以-8,根据不等式得基本性质逐一判断即可得.
【解答】解:A、将m>n两边都减2得:m-2>n-2,此选项错误;
B、将m>n两边都除以4得:,此选项正确;
C、将m>n两边都乘以6得:6m>6n,此选项错误;
D、将m>n两边都乘以-8,得:-8m<-8n,此选项错误;
故选:B.
【点评】本题主要考查不等式的性质,解题的关键是掌握不等式的基本性质,尤其是性质不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变.
(
???
思维升华
???
应用不等式的性质应注意的问题是:在不等式的两边都乘以(或除以)同一个负数时,一定要改变不等号的方向;当不等式的两边要乘以(或除以)含有字母的数时,一定要对字母是否大于
0
进行分类讨论
。
)
跟踪训练
1.(2018?宿迁)若a<b,则下列结论不一定成立的是( )
A.a-1<b-1 B.2a<2b C. D.a2<b2
【思路分析】由不等式的性质进行计算并作出正确的判断.
【解答】解:A、在不等式a<b的两边同时减去1,不等式仍成立,即a-1<b-1,故本选项错误;
B、在不等式a<b的两边同时乘以2,不等式仍成立,即2a<2b,故本选项错误;
C、在不等式a<b的两边同时乘以,不等号的方向改变,即,故本选项错误;
D、当a=-5,b=1时,不等式a2<b2不成立,故本选项正确;
故选:D.
【点评】考查了不等式的性质.应用不等式的性质应注意的问题:在不等式的两边都乘以(或除以)同一个负数时,一定要改变不等号的方向;当不等式的两边要乘以(或除以)含有字母的数时,一定要对字母是否大于0进行分类讨论.
考点二:解一元一次不等式
例2 (2018?南京)如图,在数轴上,点A、B分别表示数1、-2x+3.
(1)求x的取值范围;
(2)数轴上表示数-x+2的点应落在 .
A.点A的左边?????????? B.线段AB上????????????? C.点B的右边
【思路分析】(1)根据数轴上的点表示的数右边的总比左边的大,可得不等式,根据解不等式,可得答案;
(2)根据不等式的性质,可得点在A点的右边,根据作差法,可得点在B点的左边.
【解答】解:(1)由数轴上的点表示的数右边的总比左边的大,得
-2x+3>1,
解得x<1;
(2)由x<1,得
-x>-1.
-x+2>-1+2,
解得-x+2>1.
数轴上表示数-x+2的点在A点的右边;
作差,得
-2x+3-(-x+2)=-x+1,
由x<1,得
-x>-1,
-x+1>0,
-2x+3-(-x+2)>0,
∴-2x+3>-x+2,
数轴上表示数-x+2的点在B点的左边.
故选:B.
【点评】本题考查了一元一次不等式,解(1)的关键是利用数轴上的点表示的数右边的总比左边的大得出不等式;解(2)的关键是利用不等式的性质。
(
●●●
触
雷
警示
●●●
解一元一次不等式的易错点
解一元一次不等式并用数轴表示解集时,最易出错的有以下三点:
(
1
)去分母时常数项漏项;
(
2
)两边同乘负数时,不等号方向忘记改变;
(
3
)用数轴表示解集时,忽略“实心圆点”与“空心圆圈”的区别。
)
跟踪训练
2.(2018?桂林)解不等式,并把它的解集在数轴上表示出来.
【思路分析】根据解一元一次不等式的步骤:①去分母;②去括号;③移项;④合并同类项;⑤化系数为1.依次计算可得.
【解答】解:去分母,得:5x-1<3x+3,
移项,得:5x-3x<3+1,
合并同类项,得:2x<4,
系数化为1,得:x<2,
将不等式的解集表示在数轴上如下:
【点评】本题主要考查解一元一次不等式,解题的关键是掌握解不等式的步骤:①去分母;②去括号;③移项;④合并同类项;⑤化系数为1.
考点三:解一元一次不等式组
例3 (2018?永州)解不等式组,并把解集在数轴上表示出来.
【思路分析】分别解不等式组的两个不等式,即可得到其公共部分,依据解集即可在数轴上表示出来.
【解答】解:,
解不等式①,可得
x<3,
解不等式②,可得
x>-1,
∴不等式组的解集为-1<x<3,
在数轴上表示出来为:
【点评】本题主要考查了解一元一次不等式组,解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.
例4(2018?娄底)已知:[x]表示不超过x的最大整数.例:[3.9]=3,[-1.8]=-2.令关于k的函数 (k是正整数).例: .则下列结论错误的是( )
A.f(1)=0 B.f(k+4)=f(k) C.f(k+1)≥f(k) D.f(k)=0或1
【思路分析】根据题意可以判断各个选项是否正确,从而可以解答本题.
【解答】解:,故选项A正确;
,故选项B正确;
C、当k=3时, ,而f(3)=1,故选项C错误;
D、当k=3+4n(n为自然数)时,f(k)=1,当k为其它的正整数时,f(k)=0,所以D选项的结论正确;
选:C.
【点评】本题考查解一元一次不等式组、函数值,解答本题的关键是明确题意,可以判断各个选项中的结论是否成立.
(
???
思维升华
???
用数轴表示不等式的解集时,要注意
“
两定
”
:
一是定界点,一般在数轴上只标出原点和界点即可.定边界点时要注意,点是实心还是空心,若边界点含于解集为实心点,不含于解集即为空心点;
二是定方向,定方向的原则是:
“
小于向左,大于向右
”
。
)
跟踪训练
3.(2018?怀化)解不等式组 ,并把它的解集在数轴上表示出来.
【思路分析】分别解两不等式,进而得出公共解集.
【解答】解:解①得:x≤4,
解②得:x>2,
故不等式组的解为:2<x≤4,
解集在数轴上表示为:
【点评】此题主要考查了解一元一次不等式组的解法,正确掌握基本解题思路是解题关键.
4.(2018?聊城)若x为实数,则[x]表示不大于x的最大整数,例如[1.6]=1,[π]=3,[-2.82]=-3等.[x]+1是大于x的最小整数,对任意的实数x都满足不等式[x]≤x<[x]+1.①利用这个不等式①,求出满足[x]=2x-1的所有解,其所有解为 .
【思路分析】根据题意可以列出相应的不等式,从而可以求得x的取值范围,本题得以解决.
【解答】解:∵对任意的实数x都满足不等式[x]≤x<[x]+1,[x]=2x-1,
∴2x-1≤x<2x-1+1,
解得,0<x≤1,
∵2x-1是整数,
∴x=0.5或x=1,
故答案为:x=0.5或x=1.
【点评】本题考查了解一元一次不等式组,解答本题的关键是明确题意,会解答一元一次不等式.
考点四:不等式(组)的整数解
例5 (2018?德阳)如果关于x的不等式组的整数解仅有x=2、x=3,那么适合这个不等式组的整数a、b组成的有序数对(a,b)共有( )
A.3个 B.4个 C.5个 D.6个
【思路分析】求出不等式组的解集,根据已知求出,求出2<a≤4、9≤b<12,即可得出答案.
【解答】解:解不等式2x-a≥0,得: ,
解不等式3x-b≤0,得:x≤,
∵不等式组的整数解仅有x=2、x=3,
则,
解得:2<a≤4、9≤b<12,
则a=3时,b=9、10、11;
当a=4时,b=9、10、11;
所以适合这个不等式组的整数a、b组成的有序数对(a,b)共有6个,
故选:D.
【点评】本题考查了解一元一次不等式组,不等式组的整数解,有序实数对的应用,解此题的根据是求出a、b的值.
(
???
思维升华
???
解决
“
一元一次不等式组的整数解问题
”
的关键在于
:
正确解得不等式组或不等式的解集,然后再根据题目中对于解集的限制得到下一步所需要的条件,再根据得到的条件进而求得不等式组的整数解
。
)
跟踪训练
5.(2018?泰安)不等式组有3个整数解,则a的取值范围是( )
A.-6≤a<-5 B.-6<a≤-5 C.-6<a<-5 D.-6≤a≤-5
【思路分析】根据解不等式组,可得不等式组的解,根据不等式组的解有3个整数解,可得答案.
【解答】解:不等式组,
由,解得:x>4,
由4(x-1)≤2(x-a),解得:x≤2-a,
故不等式组的解为:4<x≤2-a,
由关于x的不等式组有3个整数解,
解得:7≤2-a<8,
解得:-6<a≤-5.
故选:B.
【点评】本题考查了一元一次不等式组,利用不等式的解得出关于a的不等式是解题关键.
考点五:确定不等式(组)中字母的取值范围
例6 (2018?呼和浩特)若不等式组的解集中的任意x,都能使不等式x-5>0成立,则a的取值范围是 .
【思路分析】先求出每个不等式的解集,再根据已知得出关于a的不等式,求出不等式的解集,再判断即可.
【解答】解:,
∵解不等式①得:x>-,
解不等式②得:x>-a+2,
∴不等式组的解集为x>-a+2,
∵不等式x-5>0的解集是x>5,
又∵不等式组的解集中的任意x,都能使不等式x-5>0成立,
∴-a+2≥5,
解得:a≤-6,
故答案为:a≤-6.
【点评】本题考查了解一元一次不等式和解一元一次不等式组,能得出关于a的不等式是解此题的关键.
跟踪训练
6.(2018?湖北)若关于x的一元一次不等式组的解集是x>3,则m的取值范围是( )
A.m>4 B.m≥4 C.m<4 D.m≤4
【思路分析】先求出每个不等式的解集,再根据不等式组的解集和已知得出关于m的不等式,再求出解集即可.
【解答】解:,
∵解不等式①得:x>3,
解不等式②得:x>m-1,
又∵关于x的一元一次不等式组的解集是x>3,
∴m-1≤3,
解得:m≤4,
故选:D.
【点评】本题考查了解一元一次不等式组,能根据不等式的解集和已知得出关于m的不等式是解此题的关键.
考点六:一元一次不等式(组)的应用
例7 (2018?赤峰)小明同学三次到某超市购买A、B两种商品,其中仅有一次是有折扣的,购买数量及消费金额如下表:
类别
次数 购买A商品数量(件) 购买B商品数量(件) 消费金额(元)
第一次 4 5 320
第二次 2 6 300
第三次 5 7 258
解答下列问题:
(1)第 次购买有折扣;
(2)求A、B两种商品的原价;
(3)若购买A、B两种商品的折扣数相同,求折扣数;
(4)小明同学再次购买A、B两种商品共10件,在(3)中折扣数的前提下,消费金额不超过200元,求至少购买A商品多少件.
【思路分析】(1)由第三次购买的A、B两种商品均比头两次多,总价反而少,可得出第三次购物有折扣;
(2)设A商品的原价为x元/件,B商品的原价为y元/件,根据总价=单价×数量结合前两次购物的数量及总价,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(3)设折扣数为z,根据总价=单价×数量,即可得出关于z的一元一次方程,解之即可得出结论;
(4)设购买A商品m件,则购买B商品(10-m)件,根据总价=单价×数量结合消费金额不超过200元,即可得出关于m的一元一次不等式,解之取其中的最小整数即可得出结论.
【解答】解:(1)观察表格数据,可知:第三次购买的A、B两种商品均比头两次多,总价反而少,
∴第三次购买有折扣.
故答案为:三.
(2)设A商品的原价为x元/件,B商品的原价为y元/件,
根据题意得: ,
解得: .
答:A商品的原价为30元/件,B商品的原价为40元/件.
(3)设折扣数为z,
根据题意得:,
解得:z=6.
答:折扣数为6.
(4)设购买A商品m件,则购买B商品(10-m)件,
根据题意得: ,
解得:m≥,
∵m为整数,
∴m的最小值为7.
答:至少购买A商品7件.
【点评】本题考查了一元一次方程的应用、二元一次方程组的应用以及一元一次不等式的应用,解题的关键是:(1)观察三次购物的数量及总价,找出哪次购物有折扣;(2)找准等量关系,正确列出二元一次方程组;(3)找准等量关系,正确列出一元一次方程;(4)根据各数量间的关系,正确列出一元一次不等式.
例8(2018?湘潭)湘潭市继2017年成功创建全国文明城市之后,又准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
【思路分析】(1)根据“购买2个温馨提示牌和3个垃圾箱共需550元”,建立方程求解即可得出结论;
(2)根据“费用不超过10000元和至少需要安放48个垃圾箱”,建立不等式即可得出结论.
【解答】解:(1)设温馨提示牌的单价为x元,则垃圾箱的单价为3x元,
根据题意得,2x+3×3x=550,
∴x=50,
经检验,符合题意,
∴3x=150元,
即:温馨提示牌和垃圾箱的单价各是50元和150元;
(2)设购买温馨提示牌y个(y为正整数),则垃圾箱为(100-y)个,
根据题意得,意, ,
∴50≤y≤52,
∵y为正整数,
∴y为50,51,52,共3种方案;
即:温馨提示牌50个,垃圾箱50个;温馨提示牌51个,垃圾箱49个;温馨提示牌52个,垃圾箱48个,
根据题意,费用为50y+150(100-y)=-100y+15000,
当y=52时,所需资金最少,最少是9800元.
【点评】此题主要考查了一元一次不等式组,一元一次方程的应用,正确找出相等关系是解本题的关键.
(
???
思维升华
???
运用不等式解决实际问题时,关键是分析问题中的数量关系,要注意抓住问题中的关键字,如“至少”、“不低于”、“不超过”、“不少于”等,找出不等关系,从而列出不等式求解。
)
【跟踪训练】
7.(2018?昆明)(列方程(组)及不等式解应用题)
水是人类生命之源.为了鼓励居民节约用水,相关部门实行居民生活用水阶梯式计量水价政策.若居民每户每月用水量不超过10立方米,每立方米按现行居民生活用水水价收费(现行居民生活用水水价=基本水价+污水处理费);若每户每月用水量超过10立方米,则超过部分每立方米在基本水价基础上加价100%,每立方米污水处理费不变.甲用户4月份用水8立方米,缴水费27.6元;乙用户4月份用水12立方米,缴水费46.3元.(注:污水处理的立方数=实际生活用水的立方数)。
(1)求每立方米的基本水价和每立方米的污水处理费各是多少元?
(2)如果某用户7月份生活用水水费计划不超过64元,该用户7月份最多可用水多少立方米?
【思路分析】(1)设每立方米的基本水价是x元,每立方米的污水处理费是y元,然后根据等量关系即可列出方程求出答案.
(2)设该用户7月份可用水t立方米(t>10),根据题意列出不等式即可求出答案.
【解答】解:(1)设每立方米的基本水价是x元,每立方米的污水处理费是y元
,
解得: ,
答:每立方米的基本水价是2.45元,每立方米的污水处理费是1元.
(2)设该用户7月份可用水t立方米(t>10),
10×2.45+(t-10)×4.9+t≤64,
解得:t≤15,
答:如果某用户7月份生活用水水费计划不超过64元,该用户7月份最多可用水15立方米
【点评】本题考查学生的应用能力,解题的关键是根据题意列出方程和不等式,本题属于中等题型.
8.(2018?济宁)“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 清理养鱼网箱人数/人 清理捕鱼网箱人数/人 总支出/元
A 15 9 57000
B 10 16 68000
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
【思路分析】(1)设清理养鱼网箱的人均费用为x元,清理捕鱼网箱的人均费用为y元,根据A、B两村庄总支出列出关于x、y的方程组,解之可得;
(2)设m人清理养鱼网箱,则(40-m)人清理捕鱼网箱,根据“总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数”列不等式组求解可得.
【解答】解:(1)设清理养鱼网箱的人均费用为x元,清理捕鱼网箱的人均费用为y元,
根据题意,得: ,
解得: ,
答:清理养鱼网箱的人均费用为2000元,清理捕鱼网箱的人均费用为3000元;
(2)设m人清理养鱼网箱,则(40-m)人清理捕鱼网箱,
根据题意,得: ,
解得:18≤m<20,
∵m为整数,
∴m=18或m=19,
则分配清理人员方案有两种:
方案一:18人清理养鱼网箱,22人清理捕鱼网箱;
方案二:19人清理养鱼网箱,21人清理捕鱼网箱.
【点评】本题主要考查二元一次方程组和一元一次不等式组的应用,解题的关键是理解题意,找到题目蕴含的相等关系或不等关系,并据此列出方程或不等式组.
(
?
??
感悟中考
?
??
分析
课程标准
和近五年的中考试题,可以发现中考命题主要集中在:实数的相反数、绝对值、倒数、科学记数法,题型一般为选择题和填空题,通过近五年考题的规律,
可以预测未来中考试题中
,实数的概念、科学记数法仍会作为重点进行考查。
)
★★★真题达标演练★★★
一、选择题
1.(2017?株洲)已知实数a,b满足a+1>b+1,则下列选项错误的为( )
A.a>b B.a+2>b+2 C.-a<-b D.2a>3b
【思路分析】根据不等式的性质即可得到a>b,a+2>b+2,-a<-b.
【解答】解:由不等式的性质得a>b,a+2>b+2,-a<-b.
故选:D.
【点评】本题考查了不等式的性质,属于基础题.
2.(2018?长春)不等式3x-6≥0的解集在数轴上表示正确的是( )
A. B.
C. D.
【思路分析】先求出不等式的解集,再在数轴上表示出来即可.
【解答】解:3x-6≥0,
3x≥6,
x≥2,
在数轴上表示为:
,
故选:B.
【点评】本题考查了解一元一次不等式和在数轴上表示不等式的解集,能求出不等式的解集是解此题的关键.
3.(2018?株洲)下列哪个选项中的不等式与不等式5x>8+2x组成的不等式组的解集为<x<5( )
A.x+5<0 B.2x>10 C.3x-15<0 D.-x-5>0
【思路分析】首先计算出不等式5x>8+2x的解集,再根据不等式的解集确定方法:大小小大中间找可确定另一个不等式的解集,进而选出答案.
【解答】解:5x>8+2x,
解得:x>,
根据大小小大中间找可得另一个不等式的解集一定是x<5,
故选:C.
【点评】此题主要考查了不等式的解集,关键是正确理解不等式组解集的确定方法:大大取大,小小取小,大小小大中间找,大大小小找不着.
4.(2018?海南)下列四个不等式组中,解集在数轴上表示如图所示的是( )
A. B. C. D.
【思路分析】根据不等式组的表示方法,可得答案.
【解答】解:由解集在数轴上的表示可知,该不等式组为,
故选:D.
【点评】本题考查了在数轴上表示不等式的解集,利用不等式组的解集的表示方法:大小小大中间找是解题关键.
5.(2018?湘西州)不等式组 的解集在数轴上表示正确的是( )
A. B.
C. D.
【思路分析】先定界点,再定方向即可得.
【解答】解:不等式组的解集在数轴上表示如下:
故选:C.
【点评】本题考查了在数轴上表示不等式的解集,用数轴表示不等式的解集时,要注意“两定”:一是定界点,一般在数轴上只标出原点和界点即可.定边界点时要注意,点是实心还是空心,若边界点含于解集为实心点,不含于解集即为空心点;
二是定方向,定方向的原则是:“小于向左,大于向右”.
6.(2018?长沙)不等式组 的解集在数轴上表示正确的是( )
A. B.
C. D.
【思路分析】先求出各不等式的解集,再求出其公共解集即可.
【解答】解:解不等式x+2>0,得:x>-2,
解不等式2x-4≤0,得:x≤2,
则不等式组的解集为-2<x≤2,
将解集表示在数轴上如下:
故选:C.
【点评】本题主要考查解一元一次不等式组,要遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.
7.(2018?恩施州)关于x的不等式组 的解集为x>3,那么a的取值范围为( )
A.a>3 B.a<3 C.a≥3 D.a≤3
【思路分析】先解第一个不等式得到x>3,由于不等式组的解集为x>3,则利用同大取大可得到a的范围.
【解答】解:解不等式2(x-1)>4,得:x>3,
解不等式a-x<0,得:x>a,
∵不等式组的解集为x>3,
∴a≤3,
故选:D.
【点评】本题考查了解一元一次不等式组:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.
8.(2018?临沂)不等式组 的正整数解的个数是( )
A.5 B.4 C.3 D.2
【思路分析】先解不等式组得到-1<x≤3,再找出此范围内的正整数.
【解答】解:解不等式1-2x<3,得:x>-1,
解不等式,得:x≤3,
则不等式组的解集为-1<x≤3,
所以不等式组的正整数解有1、2、3这3个,
故选:C.
【点评】本题考查了一元一次不等式组的整数解:利用数轴确定不等式组的解(整数解).解决此类问题的关键在于正确解得不等式组或不等式的解集,然后再根据题目中对于解集的限制得到下一步所需要的条件,再根据得到的条件进而求得不等式组的整数解.
二、填空题
9.(2018?安徽)不等式的解集是 .
【思路分析】根据解一元一次不等式得基本步骤依次计算可得.
【解答】解:去分母,得:x-8>2,
移项,得:x>2+8,
合并同类项,得:x>10,
故答案为:x>10.
【点评】本题考查了解一元一次不等式:有分母先去分母,再去括号,然后进行移项,把含未知数的项移到不等式的左边,再进行合并同类项,最后把未知数的系数化为1可得到不等式的解集.
10.(2018?黔西南州)不等式组 的解集是 .
【思路分析】首先把两个不等式的解集分别解出来,再根据大大取大,小小取小,比大的小比小的大取中间,比大的大比小的小无解的原则,把不等式的解集用一个式子表示出来.
【解答】解:由(1)x<4,由(2)x<3,所以x<3.
【点评】本题考查不等式组的解法,一定要把每个不等式的解集正确解出来.
11.(2018?贵阳)已知关于x的不等式组无解,则a的取值范围是 .
【思路分析】先把a当作已知条件求出各不等式的解集,再根据不等式组无解求出a的取值范围即可.
【解答】解:,
由①得:x≤2,
由②得:x>a,
∵不等式组无解,
∴a≥2,
故答案为:a≥2.
【点评】此题主要考查了解一元一次不等式组,关键是掌握解集的规律:同大取大;同小取小;大小小大中间找;大大小小解没了.
12.(2018?黑龙江)不等式组 有3个整数解,则a的取值范围是 .
【思路分析】先解x的不等式组,然后根据整数解的个数确定a的取值范围.
【解答】解:解不等式x-a>0,得:x>a,
解不等式1-x>2x-5,得:x<2,
∵不等式组有3个整数解,
∴不等式组的整数解为-1、0、1,
则-2≤a<-1,
故答案为:-2≤a<-1.
【点评】本题考查了一元一次不等式组的整数解,难度适中,关键是根据整数解确定关于a的不等式组.
13.(2018?包头)不等式组的非负整数解有 个.
【思路分析】首先正确解不等式组,根据它的解集写出其非负整数解.
【解答】解:解不等式2x+7>3(x+1),得:x<4,
解不等式,得:x≤8,
则不等式组的解集为x<4,
所以该不等式组的非负整数解为0、1、2、3这4个,
故答案为:4.
【点评】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
14.(2018?山西)2018年国内航空公司规定:旅客乘机时,免费携带行李箱的长,宽,高三者之和不超过115cm.某厂家生产符合该规定的行李箱.已知行李箱的宽为20cm,长与高的比为8:11,则符合此规定的行李箱的高的最大值为 cm.
【思路分析】利用长与高的比为8:11,进而利用携带行李箱的长、宽、高三者之和不超过115cm得出不等式求出即可.
【解答】解:设长为8x,高为11x,
由题意,得:19x+20≤115,
解得:x≤5,
故行李箱的高的最大值为:11x=55,
答:行李箱的高的最大值为55厘米.
故答案为:55
【点评】此题主要考查了一元一次不等式的应用,根据题意得出正确不等关系是解题关键.
三、解答题
15.(2018?威海)解不等式组,并将解集在数轴上表示出来.
【思路分析】根据解一元一次不等式组的步骤,大小小大中间找,可得答案
【解答】解:解不等式①,得x>-4,
解不等式②,得x≤2,
把不等式①②的解集在数轴上表示如图:
,
原不等式组的解集为-4<x≤2.
【点评】本题考查了解一元一次不等式组,利用不等式组的解集的表示方法是解题关键.
16.(2018?天津)解不等式组 ,请结合题意填空,完成本题的解答.
(I)解不等式①,得 ;
(l1)解不等式②,得 ;
(Ⅲ)把不等式①和②的解集在数轴上表示出来;
(Ⅳ)原不等式组的解集为 .
【思路分析】先求出不等式组中每一个不等式的解集,再求出它们的公共部分,然后把不等式的解集表示在数轴上即可.
【解答】解:,
(I)解不等式①,得x≥-2;
(Ⅱ)解不等式②,得x≤1;
(Ⅲ)把不等式①和②的解集在数轴上表示出来为:
(Ⅳ)原不等式组的解集为-2≤x≤1.
故答案为:x≥-2,x≤1,-2≤x≤1.
【点评】此题考查了解一元一次不等式,其步骤为:去分母,去括号,移项合并,将未知数系数化为1,求出解集.
17.(2018?资阳)为了美化市容市貌,政府决定将城区旁边一块162亩的荒地改建为湿地公园,规划公园分为绿化区和休闲区两部分.
(1)若休闲区面积是绿化区面积的20%,求改建后的绿化区和休闲区各有多少亩?
(2)经预算,绿化区的改建费用平均每亩35000元,休闲区的改建费用平均每亩25000元,政府计划投入资金不超过550万元,那么绿化区的面积最多可以达到多少亩?
【思路分析】(1)设改建后的绿化区面积为x亩.根据总面积为162构建方程即可解决问题;
(2)设绿化区的面积为m亩.根据投入资金不超过550万元,根据不等式即可解决问题;
【解答】解:(1)设改建后的绿化区面积为x亩.
由题意:x+20%?x=162,
解得x=135,
162-135=27,
答:改建后的绿化区面积为135亩和休闲区面积有27亩.
(2)设绿化区的面积为m亩.
由题意:35000m+25000(162-m)≤5500000,
解得m≤145,
答:绿化区的面积最多可以达到145亩.
【点评】本题考查一元一次方程的应用,一元一次不等式的应用等知识,解题的关键是学会设未知数,寻找等量关系,构建方程或不等式解决问题.
18.(2018?南通)小明购买A,B两种商品,每次购买同一种商品的单价相同,具体信息如下表:
次数 购买数量(件) 购买总费用(元)
A B
第一次 2 1 55
第二次 1 3 65
根据以上信息解答下列问题:
(1)求A,B两种商品的单价;
(2)若第三次购买这两种商品共12件,且A种商品的数量不少于B种商品数量的2倍,请设计出最省钱的购买方案,并说明理由.
【思路分析】(1)根据表格中数据进而得出等式组成方程组求出答案;
(2)利用A种商品的数量不少于B种商品数量的2倍,得出商品数量的取值范围,进而求出答案.
【解答】解:(1)设A种商品的单价为x元,B种商品的单价为y元,根据题意可得: ,
解得: ,
答:A种商品的单价为20元,B种商品的单价为15元;
(2)设第三次购买商品A种a件,则购买B种商品(12-a)件,根据题意可得:
a≥2(12-a),
得:8≤a≤12,
∵m=20a+15(12-a)=5a+180,
∴当a=8时所花钱数最少,即购买A商品8件,B商品4件.
【点评】此题主要考查了二元一次方程组的应用以及一元一次不等式的应用,正确得出等量关系是解题关键.
同课章节目录
