人教版高中数学理科选修2-1同步练习题、期中、期末复习资料、补习资料:31【提高】空间向量及其线性运算
文档属性
| 名称 | 人教版高中数学理科选修2-1同步练习题、期中、期末复习资料、补习资料:31【提高】空间向量及其线性运算 |

|
|
| 格式 | zip | ||
| 文件大小 | 965.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-20 00:00:00 | ||
图片预览




文档简介
空间向量及其线性运算
【学习目标】
1. 理解空间向量的概念,掌握空间向量的几何表示方法与字母表示方法.
2.掌握空间向量的线性运算(加法、减法和数乘)及其运算律.
3.掌握空间向量的共线定理和共面定理,并能用它们分析解决有关问题.
【要点梳理】
要点一、空间向量的相关概念
1.空间向量的定义:
在空间,我们把具有大小和方向的量叫做向量。
与平面向量一样,空间向量也用有向线段表示;记作:或。
(要注意印刷体用a,而手写体为,要区分开)
要点诠释:
(1)空间中点的一个平移就是一个向量;
(2)数学中讨论的向量与向量的起点无关,只与大小和方向有关,只要不改变大小和方向,空间向量可在空间内任意平移,故我们称之为自由向量。
2.空间向量的长度(模):
表示空间向量的有向线段的长度叫做向量的长度或模,记作或
3.空间向量的有关概念:
零向量:长度为0或者说起点和终点重合的向量,记为。规定:与任意向量平行。
单位向量:长度为1的空间向量,即.
相等向量:方向相同且模相等的向量。
相反向量:方向相反但模相等的向量。
共线向量:如果表示空间向量的有向线段所在的直线互相平行或重合,则这些向量叫做共线向量或平行向量.平行于记作.
共面向量:平行于同一个平面的向量,叫做共面向量。
要点诠释:
①当我们说向量、共线(或//)时,表示、的有向线段所在的直线可能是同一直线,也可能是平行直线.
②向量在空间中是可以平移的.空间任意两个向量都可以平移到同一个平面内,因此我们说空间任意两个向量是共面的.
要点二、空间向量的加减法
1.加减法定义
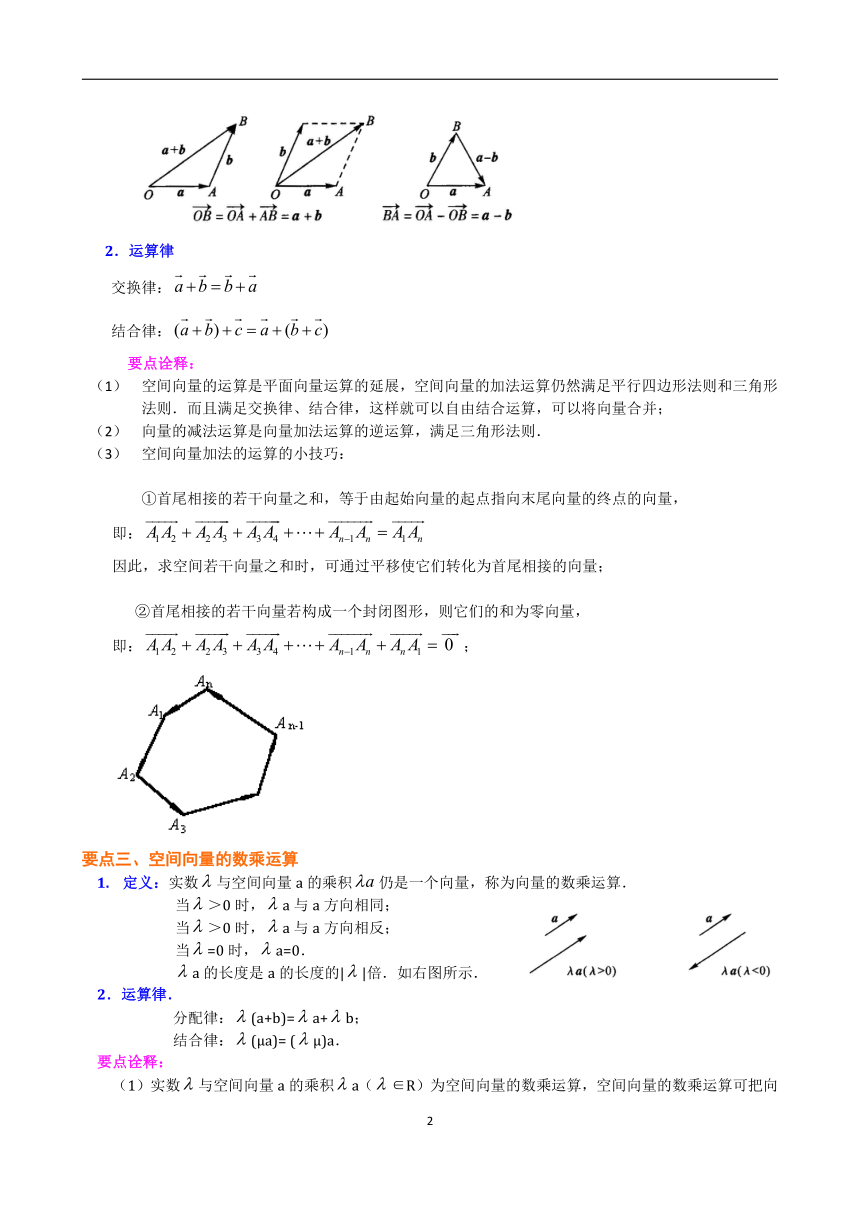
空间中任意两个向量都是共面的,它们的加、减法运算类似于平面向量的加减法.(如下图).
2.运算律
交换律:
结合律:
要点诠释:
空间向量的运算是平面向量运算的延展,空间向量的加法运算仍然满足平行四边形法则和三角形法则.而且满足交换律、结合律,这样就可以自由结合运算,可以将向量合并;
向量的减法运算是向量加法运算的逆运算,满足三角形法则.
空间向量加法的运算的小技巧:
①首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量,
即:
因此,求空间若干向量之和时,可通过平移使它们转化为首尾相接的向量;
②首尾相接的若干向量若构成一个封闭图形,则它们的和为零向量,
即:;
要点三、空间向量的数乘运算
定义:实数与空间向量a的乘积仍是一个向量,称为向量的数乘运算.
当>0时,a与a方向相同;
当>0时,a与a方向相反;
当=0时,a=0.
a的长度是a的长度的||倍.如右图所示.
2.运算律.
分配律:(a+b)=a+b;
结合律:(μa)= (μ)a.
要点诠释:
(1)实数与空间向量a的乘积a(∈R)为空间向量的数乘运算,空间向量的数乘运算可把向量伸长或缩短或改为反方向的向量,当0<<1时,向量缩短;当>1时,向量伸长;当<0时,改为反方向的向量.
(2)注意实数与向量的积的特殊情况,当=0时,a=0;当≠0时.若a≠0时,有a≠0.
(3)实数与向量可以求积,但是不能进行加减运算,比如:+a,-a无意义.
要点四、共线定理
1.共线向量的定义.
与平面向量一样,如果表示空间向量的有向线段所在的直线互相平行或重合,则这些向量叫做共线向量或平行向量,记作a∥b.
注意: 0与任意向量是共线向量.
2.共线向量定理.
空间任意两个向量、(≠),//的充要条件是存在实数,使.
要点诠释:此定理可分解为以下两个命题:
a∥b(b≠0)存在唯一实数,使得a=b;
存在唯一实数,使得a=b(b≠0),则a∥b.
注意: b≠0不可丢掉,否则实数就不唯一.
3. 共线向量定理的用途:
①判定两条直线平行;(进而证线面平行)
②证明三点共线。 注意:证明平行时,先从两直线上取有向线段表示两个向量,然后利用向量的线性运算证明向量共线,进而可以得到线线平行,这是证明平行问题的一种重要方法。证明三点共线问题,通常不用图形,直接利用向量的线性运算即可,但一定要注意所表示的向量必须有一个公共点。
要点五、共面定理
1.共面向量的定义.
通常把平行于同一平面的向量,叫做共面向量.
注意: 空间任两个向量是共面的,但空间任三个向量就不一定共面了.
2.共面向量定理.
如果两个向量不共线,与向量共面的充要条件是存在唯一的有序
实数对(),使.
推论:空间一点位于平面内的充分必要条件是存在有序实数对,使 或对空间任一点,有,
上式叫做平面的向量表达式.
3.共面向量定理的用途:
①证明四点共面
②线面平行(进而证面面平行)。
【典型例题】
类型一:空间向量的线性运算
例1.(2018春 南昌期中)如图,空间四边形OABC中,,,,点M在线段OA上,且OM=2MA,点N为BC的中点,则=( )
A. B.
C. D.
【思路点拨】由题意,把,,三个向量看作是基向量,由图形根据向量的线性运算,将用三个基向量表示出来,即可得到答案,选出正确选项。
【解析】
∵,,,
∴,
故选:A。
【总结升华】本题考点是空间向量基本定理,考查了用向量表示几何的量,向量的线性运算,解题的关键是根据图形把所研究的向量用三个基向量表示出来,本题是向量的基础题。
举一反三:
【变式1】如图:在平行六面体中,为与的交点。若,,,则下列向量中与相等的向量是( )
【答案】A 显然。
【变式2】(2018春 遂宁校级期末)已知空间四边形OABC,M,N分别是OA,BC的中点,且,,,用,,表示向量为( )
A. B.
C. D.
【答案】C
【解析】如图所示,连接ON,AN,
则
,
所以。
故选C。
例2、如右图,在长方体ABCD—A1B1C1D1中,下列各式中运算结果为向量的是( ).
①;②;
③;④.
A.①② B.②③ C.③④ D.①④
【思路点拨】 在进行减法运算时,可将减去一个向量转化为加上这个向量的相反向量,而在进行加法运算时,首先考虑这两个向量在哪个平面内,然后像平面向量求和那样,运用向量运算定律、平行四边形法则、三角形法则及多边形法则来求解.
【解析】 ①;
②;
③;
④.
因此,①②两式的运算结果为向量,而③④两式运算的结果不为向量.故选A.
【总结升华】化简向量表达式主要是利用平行四边形法则或三角形法则,遇到减法时既可转化为加法,也可按减法法则进行运算,加、减之间可以相互转化。表达式中各向量系数相等时,根据数乘分配律,可以把相同的系数提到括号外面。
举一反三:
【变式1】如图,已知长方体,化简下列向量表达式:
(1);
(2)。
【解析】 化简向量时,一般先用平行四边形得到相等的向量或相反向量,再将它们转化为具有同一起点的向量,最后利用三角形法则或平行四边形法则化简。
(1);
(2)。
【变式2】 已知平行六面体,化简下列向量表达式,并在图中标出化简结果的向量:
(1) ;
(2) ;
【答案】 (1)
(2)
【变式3】如图,已知平行六面体ABCD—A1B1C1D1,M为A1C1与B1D1的交点,化简下列向量表达式:
(1);
(2);
(3);
(4)。
【答案】向量的加法利用平行四边形法则或三角形法则,封闭图形,首尾连接的向量的和为0。
(1);
(2);
(3);
(4)。
例3.若三棱锥O一ABC中G是ΔABC的重心,求证:.
【思路点拨】 先在ΔOBC中考虑中线OD,然后在ΔOAD中考虑G为AD的分点,分成的比是2:1,两次使用向量的运算性质,把相关向量用表示即可.
【解析】如图所示,∵G是ΔABC的重心
∴,D为BC的中点
∴
【总结升华】
(1)灵活应用向量的运算法则是解此类题目的关键;
(2)此类例题常用到结论:若OD是ΔOBC的中线,则有
举一反三:
【变式1】在如图所示的平行六面体中,求证:。
【答案】∵平行六面体的六个面均为平行四边形,
∴,,,
∴
又由于,,
∴
∴。
【变式2】如图,在四边形ABCD中,E、F分别为AD、BC的中点,试证:。
【答案】 ①
②
①+②得。
∴。
例4、已知正方体,点E是上底面的中心,求下列各式中x、y、z的值:
(1);
(2)。
【思路点拨】根据向量运算法则,用向量、、表示和,然后利用向量相等来确定x、y、z的值。
【解析】(1)∵,
又∵,
∴x=1,y=-1,z=1。
(2)∵
,
又∵,
∴,,。
【总结升华】任何空间向量都可以用三个不共面向量(即是一组基向量)唯一的表示。
举一反三:
【变式】已知是平行六面体。
(1)化简,并在图中标出其结果;
(2)设M是底面ABCD的中心、N是侧面对角线上的分点,设,试求、、的值。
【答案】
(1)如图所示
取的中点为E,则
取F为的一个三等分点,则
又,,
∴。
(表示法不唯一)
(2)
∴,,。
类型二:共线向量定理的应用
例5. 证明:在四面体中连接对棱中点的三条直线交于一点且互相平分.(此点称为四面体的重心)
【思路点拨】 如图.在四面体ABCD中,E、F、G、H、P、Q分别是所在棱的中点,要证明EF、GH、PQ相交于一点O,且O为它们的中点.
【解析】 ∵E、G分别为AB、AC的中点,∴,同理,
∴.
从而四边形EGFH为平行四边形,故其对角线EF、GH相交于一点O,且O为它们的中点.连接OP、OQ.
只要能证明向量,就可以说明P、O、Q三点共线,且O为PQ的中点.事实上,,,而O为GH的中点,∴,,.
∴,.
∴.
∴.
∴PQ经过O点,且O为PQ的中点.
即证得EF、GH、Q相交于点O,且O为它们的中点,故原命题得证.
【总结升华】 利用共线向量定理可以判定两直线平行、证明三点共线.证平行时,先从直线上取有向线段来表示两个向量,然后利用向量的线性运算证明向量共线,进而可以得到线线平行,此为证明平行问题的一种重要方法;证明三点共线问题时,通常不用图形。直接利用向量的线性运算,但一定要注意所表示的向量必须有一个公共点.
举一反三:
【变式1】设、是平面上不共线的向量,已知,,,若A、B、D三点共线,求k的值。
【答案】
由共线的向量定理列出关系式。
∵,。
又∵A、B、D三点共线,
由共线向量定理,得,∴。
【变式2】如图,在平行六面体ABCD—A1B1C1D1中,E、F、G分别是A1D1、D1D、D1C1的中点。
求证:平面EFG∥平面AB1C。
【答案】用共线向量定理证明线线平行,从而证明面面平行。
证明:设,,, 则,
∴, ∴,∴EG∥AC
又∵,
∴,∴,EF∥B1C。
又∵EG与EF相交,AC与B1C相交,
∴平面EFG∥平面AB1C。
类型三:共面向量及应用
例6.已知,从平面外一点引向量
,
(1)求证:四点共面;
(2)平面平面.
【解析】(1)∵四边形是平行四边形,∴,
∵,
∴共面;
(2)∵,又∵,
∴
所以,平面平面.
【总结升华】在用共面向量定理及其推论的充要条件进行向量共面判断的时候,首先要选择恰当的充要条件形式,然后对照形式将已知条件进行转化运算.
举一反三:
【变式】已知三点不共线,对平面外任一点,满足条件,
试判断:点与是否一定共面?
【答案】由题意:,
∴,
∴,即,
所以,点与共面.
例7.如图所示,在平行六面体ABCD-A1B1C1D1中,O是B1D1的中点,
求证:B1C∥平面ODC.
【解析】
【总结升华】
(1)利用共面向量定理证明线面平行时,只需考虑一个向量可以用平面内的两个不共线的向量表示即可.
(2)利用共面向量定理证明四点共面时,通常构造有公共起点的三个向量,用其中的两个向量线性表示另一个向量,得到向量共面,即四点共面.
举一反三:
【变式1】
已知斜三棱柱,设 , , .
在面对角线和棱上分别取点和 , ,
().求证: 与向量 , 共面.
【答案】,∴
∴ 与向量 , 共面.
【变式2】 如右图,已知矩形ABCD和矩形ADEF所在平面互相垂直,点M,N分别在对角线BD,AE上,且,.
求证:MN∥平面CDE.
【答案】
证明:如题图,因为M在BD上,且,所以.
同理.
所以
.
又与不共线,
根据向量共面的充要条件可知,,共面.
由于MN不在平面CDE内,所以MN∥平面CDE.
【巩固练习】
一、选择题
1.下列各命题中,不正确的命题的个数为( )
① ② ③ ④
A.4 B.3 C.2 D.1
2.①若A、B、C、D是空间任意四点,则有;
②|a|-|b|=|a+b|是a、b共线的充要条件;
③若a、b共线,则a与b所在直线平行;
④对空间任意一点O与不共线的三点A、B、C,若 (其中x、y、z∈R),则P、A、B、C四点共面.其中不正确命题的个数是( ).
A.1 B.2 C.3 D.4
3.(2018秋 衡阳校级期中)如图,在四面体ABCD中,E、F分别是棱AD、BC的中点,则向量与、的关系是( )
A. B.
C. D.
4.已知A、B、C三点不共线,对平面ABC外的任一点O,下列条件中能确定点M与点
A、B、C一定共面的是 ( )
A. B.
C. D.
5.(2018秋·福建校级期末)如图所示,在平行六面体ABCD—A1B1C1D1中,点E为上底面对角线A1C1的中点,若,则( )
A., B.,
C., D.,
6.(2018 四川校级模拟) 已知O是平面上一定点,A、B、C是平面上不共线的三个点,动点P满足,则点P的轨迹一定通过ΔABC的( )
A. 外心 B.内心 C. 重心 D.垂心
7.已知空间向量A,B,且,,,则一定共线的三点是( ).
A.A、B、D B.A、B、C C.B、C、D D.A、C、D
二、填空题
8.如果两个向量,不共线,则与,共面的充要条件是____________。
9.已知平行六面体,化简下列表达式:
(1) ;
(2) 。
10.如图,已知空间四边形OABC,其对角线为OB、AC,M是边OA的中点,G是△ABC的重心,则用基向量、、表示向量的表达式为 .
11.已知O是空间任意一点,A、B、C、D四点满足任意三点均不共线,但四点共面,且,则2x+3y+4z=________.
三、解答题
12.在空间四边形ABCD中,连结AC、BD,△BCD的重心为G,
化简。
13. 如图,已知空间四边形,其对角线,分别是对边的中点,点在线段上,且,用基底向量表示向量
14.如右图,在直四棱柱ABCD—A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,CD=2,E,E1,F分别是棱AD,AA1,AB的中点.
证明:直线EE1∥平面FCC1.
15. 如图,已知P是平面四边形ABCD所在平面外一点,连接PA、PB、PD.点E、F、G、H分别为△PAB、△PBC、△PCD、△PDA的重心.求证:
(1)E、F、G、H四点共面;
(2)平面EFGH∥平面ABCD.
【答案与解析】
1.【答案】D
【解析】①②③正确,④不正确。
2.【答案】C
【解析】①中四点恰好围成一封闭图形,正确;
②中当a、b同向时,应有|a|+|b|=|a+b|;
③中a、b所在直线可能重合;
④中需满足x+y+z=1,才有P、A、B、C四点共面.
3. 【答案】C
【解析】:连接AF,,故选:C。
4. 【答案】D
【解析】由
可得
即
所以,即点M与点A、B、C一定共面。
5. 【答案】A
【解析】
根据题意,得:
,
又∵,
∴,
故选:A。
6.【答案】C
【解析】
,设它们等于t,
而
表示与共线的向量
而点D是BC的中点,所以即P的轨迹一定通过三角形的重心。故选C。
7.【答案】A
【解析】∵,∴A、B、D三点共线,故选A。
8. 【答案】存在实数对(),使.
【解析】由共面定理可得。
9. 【答案】(1);(2)。
【解析】由加减法的几何意义可得。
10.【答案】 =-++
【解析】如图所示,连AG延长交BC于E,=+=+=+·(+)=+(-)+(-)=-++.
11.【答案】-1
【解析】 ,
由A、B、C、D四点共面的充要条件,知(―2x)+(―3y)+(―4z)=1,即2x+3y4z=―1。
12.【解析】设E为BC的中点,
。
13.
【解析】
∴
14.【解析】由题意知,
∵F是AB的中点,∴,
∴四边形AFCD是平行四边形,∴。
∵E,E1分别是AD,AA1的中点,
∴。
又与不共线,
根据向量共面的充要条件可知,,共面。
∵EE1不在平面FCC1内,∴EE1∥平面FCC1。
15. 【解析】
(1)连接PE、PF、PG、PH,分别延长PE、PF、PG、PH交对边于M、M、Q、R.
∵E、F、G、H分别是所在三角形的重心.
∴M、N、P、R为所在边的中点,顺次连接MNPR所得四边形为平行四边形.且有
,,,.
∵四边形MNQR为平行四边形,则
.
∴由共面向量定理得E、F、G、H四点共面.
(2)由(1)知.
∴MQ∥EC,从而EG∥面AC.
又,
∴MN∥EF,∴EF∥面AC.
又∵EG∩EF=E,∴平面EFGH∥平面ABCD.
【学习目标】
1. 理解空间向量的概念,掌握空间向量的几何表示方法与字母表示方法.
2.掌握空间向量的线性运算(加法、减法和数乘)及其运算律.
3.掌握空间向量的共线定理和共面定理,并能用它们分析解决有关问题.
【要点梳理】
要点一、空间向量的相关概念
1.空间向量的定义:
在空间,我们把具有大小和方向的量叫做向量。
与平面向量一样,空间向量也用有向线段表示;记作:或。
(要注意印刷体用a,而手写体为,要区分开)
要点诠释:
(1)空间中点的一个平移就是一个向量;
(2)数学中讨论的向量与向量的起点无关,只与大小和方向有关,只要不改变大小和方向,空间向量可在空间内任意平移,故我们称之为自由向量。
2.空间向量的长度(模):
表示空间向量的有向线段的长度叫做向量的长度或模,记作或
3.空间向量的有关概念:
零向量:长度为0或者说起点和终点重合的向量,记为。规定:与任意向量平行。
单位向量:长度为1的空间向量,即.
相等向量:方向相同且模相等的向量。
相反向量:方向相反但模相等的向量。
共线向量:如果表示空间向量的有向线段所在的直线互相平行或重合,则这些向量叫做共线向量或平行向量.平行于记作.
共面向量:平行于同一个平面的向量,叫做共面向量。
要点诠释:
①当我们说向量、共线(或//)时,表示、的有向线段所在的直线可能是同一直线,也可能是平行直线.
②向量在空间中是可以平移的.空间任意两个向量都可以平移到同一个平面内,因此我们说空间任意两个向量是共面的.
要点二、空间向量的加减法
1.加减法定义
空间中任意两个向量都是共面的,它们的加、减法运算类似于平面向量的加减法.(如下图).
2.运算律
交换律:
结合律:
要点诠释:
空间向量的运算是平面向量运算的延展,空间向量的加法运算仍然满足平行四边形法则和三角形法则.而且满足交换律、结合律,这样就可以自由结合运算,可以将向量合并;
向量的减法运算是向量加法运算的逆运算,满足三角形法则.
空间向量加法的运算的小技巧:
①首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量,
即:
因此,求空间若干向量之和时,可通过平移使它们转化为首尾相接的向量;
②首尾相接的若干向量若构成一个封闭图形,则它们的和为零向量,
即:;
要点三、空间向量的数乘运算
定义:实数与空间向量a的乘积仍是一个向量,称为向量的数乘运算.
当>0时,a与a方向相同;
当>0时,a与a方向相反;
当=0时,a=0.
a的长度是a的长度的||倍.如右图所示.
2.运算律.
分配律:(a+b)=a+b;
结合律:(μa)= (μ)a.
要点诠释:
(1)实数与空间向量a的乘积a(∈R)为空间向量的数乘运算,空间向量的数乘运算可把向量伸长或缩短或改为反方向的向量,当0<<1时,向量缩短;当>1时,向量伸长;当<0时,改为反方向的向量.
(2)注意实数与向量的积的特殊情况,当=0时,a=0;当≠0时.若a≠0时,有a≠0.
(3)实数与向量可以求积,但是不能进行加减运算,比如:+a,-a无意义.
要点四、共线定理
1.共线向量的定义.
与平面向量一样,如果表示空间向量的有向线段所在的直线互相平行或重合,则这些向量叫做共线向量或平行向量,记作a∥b.
注意: 0与任意向量是共线向量.
2.共线向量定理.
空间任意两个向量、(≠),//的充要条件是存在实数,使.
要点诠释:此定理可分解为以下两个命题:
a∥b(b≠0)存在唯一实数,使得a=b;
存在唯一实数,使得a=b(b≠0),则a∥b.
注意: b≠0不可丢掉,否则实数就不唯一.
3. 共线向量定理的用途:
①判定两条直线平行;(进而证线面平行)
②证明三点共线。 注意:证明平行时,先从两直线上取有向线段表示两个向量,然后利用向量的线性运算证明向量共线,进而可以得到线线平行,这是证明平行问题的一种重要方法。证明三点共线问题,通常不用图形,直接利用向量的线性运算即可,但一定要注意所表示的向量必须有一个公共点。
要点五、共面定理
1.共面向量的定义.
通常把平行于同一平面的向量,叫做共面向量.
注意: 空间任两个向量是共面的,但空间任三个向量就不一定共面了.
2.共面向量定理.
如果两个向量不共线,与向量共面的充要条件是存在唯一的有序
实数对(),使.
推论:空间一点位于平面内的充分必要条件是存在有序实数对,使 或对空间任一点,有,
上式叫做平面的向量表达式.
3.共面向量定理的用途:
①证明四点共面
②线面平行(进而证面面平行)。
【典型例题】
类型一:空间向量的线性运算
例1.(2018春 南昌期中)如图,空间四边形OABC中,,,,点M在线段OA上,且OM=2MA,点N为BC的中点,则=( )
A. B.
C. D.
【思路点拨】由题意,把,,三个向量看作是基向量,由图形根据向量的线性运算,将用三个基向量表示出来,即可得到答案,选出正确选项。
【解析】
∵,,,
∴,
故选:A。
【总结升华】本题考点是空间向量基本定理,考查了用向量表示几何的量,向量的线性运算,解题的关键是根据图形把所研究的向量用三个基向量表示出来,本题是向量的基础题。
举一反三:
【变式1】如图:在平行六面体中,为与的交点。若,,,则下列向量中与相等的向量是( )
【答案】A 显然。
【变式2】(2018春 遂宁校级期末)已知空间四边形OABC,M,N分别是OA,BC的中点,且,,,用,,表示向量为( )
A. B.
C. D.
【答案】C
【解析】如图所示,连接ON,AN,
则
,
所以。
故选C。
例2、如右图,在长方体ABCD—A1B1C1D1中,下列各式中运算结果为向量的是( ).
①;②;
③;④.
A.①② B.②③ C.③④ D.①④
【思路点拨】 在进行减法运算时,可将减去一个向量转化为加上这个向量的相反向量,而在进行加法运算时,首先考虑这两个向量在哪个平面内,然后像平面向量求和那样,运用向量运算定律、平行四边形法则、三角形法则及多边形法则来求解.
【解析】 ①;
②;
③;
④.
因此,①②两式的运算结果为向量,而③④两式运算的结果不为向量.故选A.
【总结升华】化简向量表达式主要是利用平行四边形法则或三角形法则,遇到减法时既可转化为加法,也可按减法法则进行运算,加、减之间可以相互转化。表达式中各向量系数相等时,根据数乘分配律,可以把相同的系数提到括号外面。
举一反三:
【变式1】如图,已知长方体,化简下列向量表达式:
(1);
(2)。
【解析】 化简向量时,一般先用平行四边形得到相等的向量或相反向量,再将它们转化为具有同一起点的向量,最后利用三角形法则或平行四边形法则化简。
(1);
(2)。
【变式2】 已知平行六面体,化简下列向量表达式,并在图中标出化简结果的向量:
(1) ;
(2) ;
【答案】 (1)
(2)
【变式3】如图,已知平行六面体ABCD—A1B1C1D1,M为A1C1与B1D1的交点,化简下列向量表达式:
(1);
(2);
(3);
(4)。
【答案】向量的加法利用平行四边形法则或三角形法则,封闭图形,首尾连接的向量的和为0。
(1);
(2);
(3);
(4)。
例3.若三棱锥O一ABC中G是ΔABC的重心,求证:.
【思路点拨】 先在ΔOBC中考虑中线OD,然后在ΔOAD中考虑G为AD的分点,分成的比是2:1,两次使用向量的运算性质,把相关向量用表示即可.
【解析】如图所示,∵G是ΔABC的重心
∴,D为BC的中点
∴
【总结升华】
(1)灵活应用向量的运算法则是解此类题目的关键;
(2)此类例题常用到结论:若OD是ΔOBC的中线,则有
举一反三:
【变式1】在如图所示的平行六面体中,求证:。
【答案】∵平行六面体的六个面均为平行四边形,
∴,,,
∴
又由于,,
∴
∴。
【变式2】如图,在四边形ABCD中,E、F分别为AD、BC的中点,试证:。
【答案】 ①
②
①+②得。
∴。
例4、已知正方体,点E是上底面的中心,求下列各式中x、y、z的值:
(1);
(2)。
【思路点拨】根据向量运算法则,用向量、、表示和,然后利用向量相等来确定x、y、z的值。
【解析】(1)∵,
又∵,
∴x=1,y=-1,z=1。
(2)∵
,
又∵,
∴,,。
【总结升华】任何空间向量都可以用三个不共面向量(即是一组基向量)唯一的表示。
举一反三:
【变式】已知是平行六面体。
(1)化简,并在图中标出其结果;
(2)设M是底面ABCD的中心、N是侧面对角线上的分点,设,试求、、的值。
【答案】
(1)如图所示
取的中点为E,则
取F为的一个三等分点,则
又,,
∴。
(表示法不唯一)
(2)
∴,,。
类型二:共线向量定理的应用
例5. 证明:在四面体中连接对棱中点的三条直线交于一点且互相平分.(此点称为四面体的重心)
【思路点拨】 如图.在四面体ABCD中,E、F、G、H、P、Q分别是所在棱的中点,要证明EF、GH、PQ相交于一点O,且O为它们的中点.
【解析】 ∵E、G分别为AB、AC的中点,∴,同理,
∴.
从而四边形EGFH为平行四边形,故其对角线EF、GH相交于一点O,且O为它们的中点.连接OP、OQ.
只要能证明向量,就可以说明P、O、Q三点共线,且O为PQ的中点.事实上,,,而O为GH的中点,∴,,.
∴,.
∴.
∴.
∴PQ经过O点,且O为PQ的中点.
即证得EF、GH、Q相交于点O,且O为它们的中点,故原命题得证.
【总结升华】 利用共线向量定理可以判定两直线平行、证明三点共线.证平行时,先从直线上取有向线段来表示两个向量,然后利用向量的线性运算证明向量共线,进而可以得到线线平行,此为证明平行问题的一种重要方法;证明三点共线问题时,通常不用图形。直接利用向量的线性运算,但一定要注意所表示的向量必须有一个公共点.
举一反三:
【变式1】设、是平面上不共线的向量,已知,,,若A、B、D三点共线,求k的值。
【答案】
由共线的向量定理列出关系式。
∵,。
又∵A、B、D三点共线,
由共线向量定理,得,∴。
【变式2】如图,在平行六面体ABCD—A1B1C1D1中,E、F、G分别是A1D1、D1D、D1C1的中点。
求证:平面EFG∥平面AB1C。
【答案】用共线向量定理证明线线平行,从而证明面面平行。
证明:设,,, 则,
∴, ∴,∴EG∥AC
又∵,
∴,∴,EF∥B1C。
又∵EG与EF相交,AC与B1C相交,
∴平面EFG∥平面AB1C。
类型三:共面向量及应用
例6.已知,从平面外一点引向量
,
(1)求证:四点共面;
(2)平面平面.
【解析】(1)∵四边形是平行四边形,∴,
∵,
∴共面;
(2)∵,又∵,
∴
所以,平面平面.
【总结升华】在用共面向量定理及其推论的充要条件进行向量共面判断的时候,首先要选择恰当的充要条件形式,然后对照形式将已知条件进行转化运算.
举一反三:
【变式】已知三点不共线,对平面外任一点,满足条件,
试判断:点与是否一定共面?
【答案】由题意:,
∴,
∴,即,
所以,点与共面.
例7.如图所示,在平行六面体ABCD-A1B1C1D1中,O是B1D1的中点,
求证:B1C∥平面ODC.
【解析】
【总结升华】
(1)利用共面向量定理证明线面平行时,只需考虑一个向量可以用平面内的两个不共线的向量表示即可.
(2)利用共面向量定理证明四点共面时,通常构造有公共起点的三个向量,用其中的两个向量线性表示另一个向量,得到向量共面,即四点共面.
举一反三:
【变式1】
已知斜三棱柱,设 , , .
在面对角线和棱上分别取点和 , ,
().求证: 与向量 , 共面.
【答案】,∴
∴ 与向量 , 共面.
【变式2】 如右图,已知矩形ABCD和矩形ADEF所在平面互相垂直,点M,N分别在对角线BD,AE上,且,.
求证:MN∥平面CDE.
【答案】
证明:如题图,因为M在BD上,且,所以.
同理.
所以
.
又与不共线,
根据向量共面的充要条件可知,,共面.
由于MN不在平面CDE内,所以MN∥平面CDE.
【巩固练习】
一、选择题
1.下列各命题中,不正确的命题的个数为( )
① ② ③ ④
A.4 B.3 C.2 D.1
2.①若A、B、C、D是空间任意四点,则有;
②|a|-|b|=|a+b|是a、b共线的充要条件;
③若a、b共线,则a与b所在直线平行;
④对空间任意一点O与不共线的三点A、B、C,若 (其中x、y、z∈R),则P、A、B、C四点共面.其中不正确命题的个数是( ).
A.1 B.2 C.3 D.4
3.(2018秋 衡阳校级期中)如图,在四面体ABCD中,E、F分别是棱AD、BC的中点,则向量与、的关系是( )
A. B.
C. D.
4.已知A、B、C三点不共线,对平面ABC外的任一点O,下列条件中能确定点M与点
A、B、C一定共面的是 ( )
A. B.
C. D.
5.(2018秋·福建校级期末)如图所示,在平行六面体ABCD—A1B1C1D1中,点E为上底面对角线A1C1的中点,若,则( )
A., B.,
C., D.,
6.(2018 四川校级模拟) 已知O是平面上一定点,A、B、C是平面上不共线的三个点,动点P满足,则点P的轨迹一定通过ΔABC的( )
A. 外心 B.内心 C. 重心 D.垂心
7.已知空间向量A,B,且,,,则一定共线的三点是( ).
A.A、B、D B.A、B、C C.B、C、D D.A、C、D
二、填空题
8.如果两个向量,不共线,则与,共面的充要条件是____________。
9.已知平行六面体,化简下列表达式:
(1) ;
(2) 。
10.如图,已知空间四边形OABC,其对角线为OB、AC,M是边OA的中点,G是△ABC的重心,则用基向量、、表示向量的表达式为 .
11.已知O是空间任意一点,A、B、C、D四点满足任意三点均不共线,但四点共面,且,则2x+3y+4z=________.
三、解答题
12.在空间四边形ABCD中,连结AC、BD,△BCD的重心为G,
化简。
13. 如图,已知空间四边形,其对角线,分别是对边的中点,点在线段上,且,用基底向量表示向量
14.如右图,在直四棱柱ABCD—A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,CD=2,E,E1,F分别是棱AD,AA1,AB的中点.
证明:直线EE1∥平面FCC1.
15. 如图,已知P是平面四边形ABCD所在平面外一点,连接PA、PB、PD.点E、F、G、H分别为△PAB、△PBC、△PCD、△PDA的重心.求证:
(1)E、F、G、H四点共面;
(2)平面EFGH∥平面ABCD.
【答案与解析】
1.【答案】D
【解析】①②③正确,④不正确。
2.【答案】C
【解析】①中四点恰好围成一封闭图形,正确;
②中当a、b同向时,应有|a|+|b|=|a+b|;
③中a、b所在直线可能重合;
④中需满足x+y+z=1,才有P、A、B、C四点共面.
3. 【答案】C
【解析】:连接AF,,故选:C。
4. 【答案】D
【解析】由
可得
即
所以,即点M与点A、B、C一定共面。
5. 【答案】A
【解析】
根据题意,得:
,
又∵,
∴,
故选:A。
6.【答案】C
【解析】
,设它们等于t,
而
表示与共线的向量
而点D是BC的中点,所以即P的轨迹一定通过三角形的重心。故选C。
7.【答案】A
【解析】∵,∴A、B、D三点共线,故选A。
8. 【答案】存在实数对(),使.
【解析】由共面定理可得。
9. 【答案】(1);(2)。
【解析】由加减法的几何意义可得。
10.【答案】 =-++
【解析】如图所示,连AG延长交BC于E,=+=+=+·(+)=+(-)+(-)=-++.
11.【答案】-1
【解析】 ,
由A、B、C、D四点共面的充要条件,知(―2x)+(―3y)+(―4z)=1,即2x+3y4z=―1。
12.【解析】设E为BC的中点,
。
13.
【解析】
∴
14.【解析】由题意知,
∵F是AB的中点,∴,
∴四边形AFCD是平行四边形,∴。
∵E,E1分别是AD,AA1的中点,
∴。
又与不共线,
根据向量共面的充要条件可知,,共面。
∵EE1不在平面FCC1内,∴EE1∥平面FCC1。
15. 【解析】
(1)连接PE、PF、PG、PH,分别延长PE、PF、PG、PH交对边于M、M、Q、R.
∵E、F、G、H分别是所在三角形的重心.
∴M、N、P、R为所在边的中点,顺次连接MNPR所得四边形为平行四边形.且有
,,,.
∵四边形MNQR为平行四边形,则
.
∴由共面向量定理得E、F、G、H四点共面.
(2)由(1)知.
∴MQ∥EC,从而EG∥面AC.
又,
∴MN∥EF,∴EF∥面AC.
又∵EG∩EF=E,∴平面EFGH∥平面ABCD.
