4.1.2圆柱的表面积说课 课件(27张ppt)
文档属性
| 名称 | 4.1.2圆柱的表面积说课 课件(27张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-19 00:00:00 | ||
图片预览







文档简介
(共27张PPT)
说课流程
1.说教材与学情分析
2.说教学目标与重难点
3.说学法、教具学具
4.说教学程序
5.说板书设计
一、
说教材
1、教材的内容、地位和作用及学生的学习基础情况。
《圆柱与圆锥》这一教学内容是小学阶段数学《空间与图形》领域中最后一个单元的知识。教材之所以这样安排,是因为在此之前,学生已经认识了长方体算,学生还认识了长方体、正方体,掌握了长(正)方体表面积与体积的含义及其计算方法,这些都是学生学习圆柱和圆锥的基础。而《圆柱的表面积》这个内容又是《圆柱和圆锥》这个单元中的一个知识点,它是学生在学习了认识了圆柱和圆锥及其基本特征后安排的一个具有探索性的内容,让学生通过想象、操作等探索活动运用迁移规律把圆柱体的侧面积、表面积的计算方法这一新知识转化到学生原有的认知结构中,即圆的面积和长方形、正方形的面积计算。另外学好这部分内容,可以进一步发展学生的空间观念,为以后学习其它几何形体打下坚实的基础。2、《空间与图形》这一知识的教学是培养学生抽象概括能力、思维能力和建立空间观念的重要途径。它是人们更好地认识和描述生活空间进行交流的重要工具,教材十分注重把学生的视野拓宽到自己生活的、正方体、圆柱和球,并初步了解了长方形、正方形、圆等平面图形的特点,学习了这些图形的面积计空间,注重以现实世界中有关空间与图形的问题作为学习素材,使学生经历用观察、操作、想象、思考等多种方式探索图形的性质、运动、位置、度量等,并能够运用所学的知识解决生活中的实际问题。
因此结合《圆柱的表面积》这一知识的特点,我将本课的教学目标拟定如下:
(1)知识教学:①通过想象和操作等活动,加深对圆柱特征的认识,理解圆柱表面积的的含义,知道圆柱的侧面展开后可以是一个长方形。②结合具体的情境和动手操作,探索圆柱侧面积的计算方法,掌握圆柱侧面积和表面积的计算方法,能正确计算圆柱的侧面积和表面积。
(2)能力训练:能根据具体情境,灵活运用圆柱表面积的计算方法解决生活中的一些简单的实际问题,体会数学与生活的联系;培养学生的观察、操作、想象能力,发展学生的空间观念,渗透转化的思想。
(3)素质培养:培养学生的探索精神和合作能力,养成良好的数学学习习惯。圆柱体的侧面积和表面积在本课教材中占重要地位,它们是学习其它几何知识的基础,所以本课的重点是:探索圆柱体侧面积、表面积的计算方法,并能运用圆柱侧面积和表面积的计算方法解决生活中的一些简单的实际问题。由于圆柱体的侧面积计算较为抽象,加之学生的空间想象力不够丰富,所以本课的难点是:理解圆柱侧面展开的多样性,将展开图与圆柱的各部分联系起来,并推导出圆柱体侧面积和表面积的计算公式。而解决这一难点的关键是:把圆柱体的侧面展开后所得到的长方形各部分同圆柱体各部分间的关系。
三、说学法
在本课的学习活动中注重培养学生的空间观念、想象力、动手操作能力、探索能力和推理概括能力。所以学生的学法以教师设计的多媒体演示为依托,以学生自备的圆柱形纸盒、长方形纸、剪刀等学具为载体,在老师的引导下进行学习活动。学习活动以小组共同探索、交流讨论、合作学习为主要形式,教师适时进行点拨,创设平等、自主、和谐的教学环境,通过学生的动手操作、观察、比较、推理、概括等充分调动学生多种感官的参与,让学生全面参与新知的发生、发展和形成过程,并学会操作、观察、比较、分析和概括,学会想象,学会与人交往。在活动中获得成功的体验,从而培养学生学习数学的兴趣,得到“人人学有价值的数学”这个目的。
四、说教学程序
五、说板书设计
圆柱的表面积
长方形的面积= 长 × 宽
圆柱的侧面积=底面周长 × 高
圆柱的表面积=圆柱的侧面积+两个底面的面
[设计意图]
这一板书把探究的圆柱表面积,尤其是侧面积与转化后长方形的长、宽之间的联系,清楚地呈现给学生。这样的板书既简单明了,又突出了重点,最主要的是加深学生对本节重难点知识的理解和掌握。)
圆的周长怎样算?
长方形的面积公式?
复习
复 习
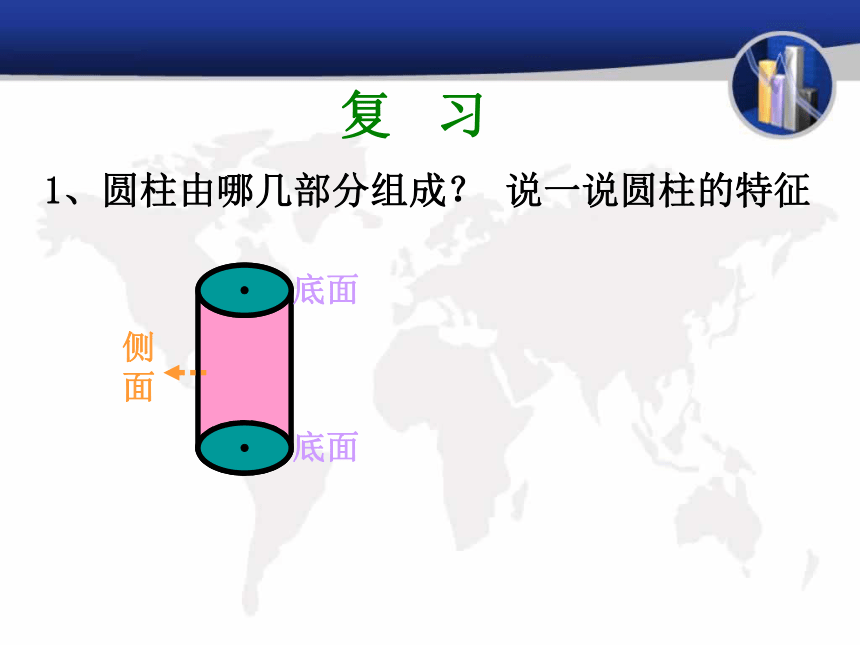
1、圆柱由哪几部分组成? 说一说圆柱的特征
底面
底面
侧面
1、圆柱有( )个底面,它们是( );有( )个侧面,是( ),有( )条高,这些高都( )。
2、圆柱的侧面展开是( ),长方形的长等于( ),宽等于( )。
3、圆柱的侧面积=
2
大小一样的圆
1
曲面
无数
长度相等
长方形
底面周长
高
底面周长×高
尝试练习:
侧 面
底面
底面
侧 面 =底面周长×高
底面=圆的面积
底面=圆的面积
侧 面 =底面周长×高
底面=圆的面积
底面=圆的面积
它们三个的···
圆柱的表面积=侧面积+两个底面的面积
字母公式
↓
S表面积=S侧+2S底
例题:1
一个圆柱,底面积是250dm2,侧面积是450dm2。求它的表面积?
S侧=250dm2 S底=450dm2
S表面积 =S侧+2S底
=450+2×250
=450+500
=950(dm2)
答:圆柱的表面积是950平方分米。
(1)侧面积:2 ×3.14 ×5 ×14=439.6(平方厘米)
(2)底面积:3.14 ×52 =78.5(平方厘米)
(3)表面积439.6+78.5× 2=596.6(平方厘米)
做一个无盖的圆柱形铁皮水桶,高是5分米。底面直径4分米,至少需要多大面积的铁皮
水桶没有盖,说明它只有一个底面。
(1)水桶的侧面积:
3.14 ×4 ×5=62.8(平方分米)
(2)水桶的底面积:
3.14 ×(4÷2) 2=12.56(平方分米)
(3)需要铁皮:
62.8+12.56=75.36(平方分米)
计算下现各圆柱的表面积。(单位:厘米)
一台压路机的滚筒宽1.2米,直径为0.8米。如果它滚动10周,压路的面积是多少平方米?
一台压路机的前轮是圆柱形,轮宽2米,滚筒直径是轮宽的60%,每分钟转动20周,每分钟压路的面积是多少平方米?
3.14×1.2×2×20
底面周长
圆柱侧面积
2×60%=1.2(米)
尝试练习:
1、把一个底面直径为5厘米,高是8厘米的圆柱体沿底面直径切开,分成形状大小完全相同的两部分,它们的表面积比原来增加多少平方厘米?
动脑筋
把下面的圆柱形木料,截成两段,它的表面积会有怎样的变化?
在实际应用中计算圆柱形物体的表面积,要根据实际情况计算各部分的面积。如计算烟筒用铁皮只求一个侧面积;水桶用铁皮是侧面积加上一个底面积;油桶用铁皮是侧面积加上两个底面积,求用料多少,一般采用进一法取值,以保证原材料够用。
课堂小结
圆柱的表面积
长方形的面积=长×宽
圆柱的侧面积=底面周长×高
圆柱的表面积=圆柱的侧面积+两个底面的面积
S表面积=S侧+2S底
说课流程
1.说教材与学情分析
2.说教学目标与重难点
3.说学法、教具学具
4.说教学程序
5.说板书设计
一、
说教材
1、教材的内容、地位和作用及学生的学习基础情况。
《圆柱与圆锥》这一教学内容是小学阶段数学《空间与图形》领域中最后一个单元的知识。教材之所以这样安排,是因为在此之前,学生已经认识了长方体算,学生还认识了长方体、正方体,掌握了长(正)方体表面积与体积的含义及其计算方法,这些都是学生学习圆柱和圆锥的基础。而《圆柱的表面积》这个内容又是《圆柱和圆锥》这个单元中的一个知识点,它是学生在学习了认识了圆柱和圆锥及其基本特征后安排的一个具有探索性的内容,让学生通过想象、操作等探索活动运用迁移规律把圆柱体的侧面积、表面积的计算方法这一新知识转化到学生原有的认知结构中,即圆的面积和长方形、正方形的面积计算。另外学好这部分内容,可以进一步发展学生的空间观念,为以后学习其它几何形体打下坚实的基础。2、《空间与图形》这一知识的教学是培养学生抽象概括能力、思维能力和建立空间观念的重要途径。它是人们更好地认识和描述生活空间进行交流的重要工具,教材十分注重把学生的视野拓宽到自己生活的、正方体、圆柱和球,并初步了解了长方形、正方形、圆等平面图形的特点,学习了这些图形的面积计空间,注重以现实世界中有关空间与图形的问题作为学习素材,使学生经历用观察、操作、想象、思考等多种方式探索图形的性质、运动、位置、度量等,并能够运用所学的知识解决生活中的实际问题。
因此结合《圆柱的表面积》这一知识的特点,我将本课的教学目标拟定如下:
(1)知识教学:①通过想象和操作等活动,加深对圆柱特征的认识,理解圆柱表面积的的含义,知道圆柱的侧面展开后可以是一个长方形。②结合具体的情境和动手操作,探索圆柱侧面积的计算方法,掌握圆柱侧面积和表面积的计算方法,能正确计算圆柱的侧面积和表面积。
(2)能力训练:能根据具体情境,灵活运用圆柱表面积的计算方法解决生活中的一些简单的实际问题,体会数学与生活的联系;培养学生的观察、操作、想象能力,发展学生的空间观念,渗透转化的思想。
(3)素质培养:培养学生的探索精神和合作能力,养成良好的数学学习习惯。圆柱体的侧面积和表面积在本课教材中占重要地位,它们是学习其它几何知识的基础,所以本课的重点是:探索圆柱体侧面积、表面积的计算方法,并能运用圆柱侧面积和表面积的计算方法解决生活中的一些简单的实际问题。由于圆柱体的侧面积计算较为抽象,加之学生的空间想象力不够丰富,所以本课的难点是:理解圆柱侧面展开的多样性,将展开图与圆柱的各部分联系起来,并推导出圆柱体侧面积和表面积的计算公式。而解决这一难点的关键是:把圆柱体的侧面展开后所得到的长方形各部分同圆柱体各部分间的关系。
三、说学法
在本课的学习活动中注重培养学生的空间观念、想象力、动手操作能力、探索能力和推理概括能力。所以学生的学法以教师设计的多媒体演示为依托,以学生自备的圆柱形纸盒、长方形纸、剪刀等学具为载体,在老师的引导下进行学习活动。学习活动以小组共同探索、交流讨论、合作学习为主要形式,教师适时进行点拨,创设平等、自主、和谐的教学环境,通过学生的动手操作、观察、比较、推理、概括等充分调动学生多种感官的参与,让学生全面参与新知的发生、发展和形成过程,并学会操作、观察、比较、分析和概括,学会想象,学会与人交往。在活动中获得成功的体验,从而培养学生学习数学的兴趣,得到“人人学有价值的数学”这个目的。
四、说教学程序
五、说板书设计
圆柱的表面积
长方形的面积= 长 × 宽
圆柱的侧面积=底面周长 × 高
圆柱的表面积=圆柱的侧面积+两个底面的面
[设计意图]
这一板书把探究的圆柱表面积,尤其是侧面积与转化后长方形的长、宽之间的联系,清楚地呈现给学生。这样的板书既简单明了,又突出了重点,最主要的是加深学生对本节重难点知识的理解和掌握。)
圆的周长怎样算?
长方形的面积公式?
复习
复 习
1、圆柱由哪几部分组成? 说一说圆柱的特征
底面
底面
侧面
1、圆柱有( )个底面,它们是( );有( )个侧面,是( ),有( )条高,这些高都( )。
2、圆柱的侧面展开是( ),长方形的长等于( ),宽等于( )。
3、圆柱的侧面积=
2
大小一样的圆
1
曲面
无数
长度相等
长方形
底面周长
高
底面周长×高
尝试练习:
侧 面
底面
底面
侧 面 =底面周长×高
底面=圆的面积
底面=圆的面积
侧 面 =底面周长×高
底面=圆的面积
底面=圆的面积
它们三个的···
圆柱的表面积=侧面积+两个底面的面积
字母公式
↓
S表面积=S侧+2S底
例题:1
一个圆柱,底面积是250dm2,侧面积是450dm2。求它的表面积?
S侧=250dm2 S底=450dm2
S表面积 =S侧+2S底
=450+2×250
=450+500
=950(dm2)
答:圆柱的表面积是950平方分米。
(1)侧面积:2 ×3.14 ×5 ×14=439.6(平方厘米)
(2)底面积:3.14 ×52 =78.5(平方厘米)
(3)表面积439.6+78.5× 2=596.6(平方厘米)
做一个无盖的圆柱形铁皮水桶,高是5分米。底面直径4分米,至少需要多大面积的铁皮
水桶没有盖,说明它只有一个底面。
(1)水桶的侧面积:
3.14 ×4 ×5=62.8(平方分米)
(2)水桶的底面积:
3.14 ×(4÷2) 2=12.56(平方分米)
(3)需要铁皮:
62.8+12.56=75.36(平方分米)
计算下现各圆柱的表面积。(单位:厘米)
一台压路机的滚筒宽1.2米,直径为0.8米。如果它滚动10周,压路的面积是多少平方米?
一台压路机的前轮是圆柱形,轮宽2米,滚筒直径是轮宽的60%,每分钟转动20周,每分钟压路的面积是多少平方米?
3.14×1.2×2×20
底面周长
圆柱侧面积
2×60%=1.2(米)
尝试练习:
1、把一个底面直径为5厘米,高是8厘米的圆柱体沿底面直径切开,分成形状大小完全相同的两部分,它们的表面积比原来增加多少平方厘米?
动脑筋
把下面的圆柱形木料,截成两段,它的表面积会有怎样的变化?
在实际应用中计算圆柱形物体的表面积,要根据实际情况计算各部分的面积。如计算烟筒用铁皮只求一个侧面积;水桶用铁皮是侧面积加上一个底面积;油桶用铁皮是侧面积加上两个底面积,求用料多少,一般采用进一法取值,以保证原材料够用。
课堂小结
圆柱的表面积
长方形的面积=长×宽
圆柱的侧面积=底面周长×高
圆柱的表面积=圆柱的侧面积+两个底面的面积
S表面积=S侧+2S底
