人教版高中数学理科选修2-2同步练习题、期中、期末复习资料、补习资料:04【提高】导数的几何意义
文档属性
| 名称 | 人教版高中数学理科选修2-2同步练习题、期中、期末复习资料、补习资料:04【提高】导数的几何意义 |
|
|
| 格式 | zip | ||
| 文件大小 | 574.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-21 00:00:00 | ||
图片预览




文档简介
导数的几何意义
【学习目标】
1.理解导数的几何意义。
2.理解导数的全面涵义。
3.掌握利用导数求函数图象的切线的斜率。
4.会求过点(或在点处)的切线方程。
【要点梳理】(根据课标要求进行适当的深化与拓展。)
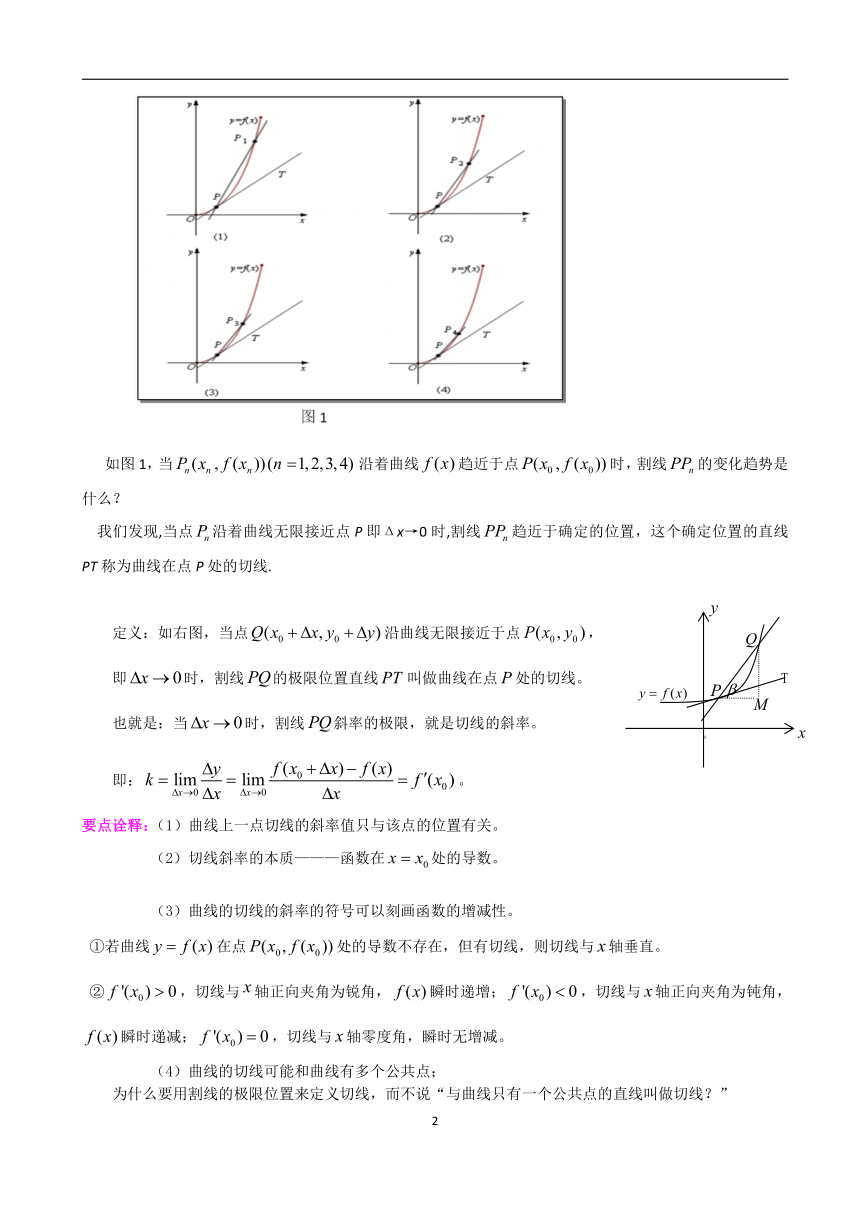
要点一、导数几何意义
平均变化率的几何意义——曲线的割线
函数的平均变化率的几何意义是表示连接函数图像上两点割线的斜率。
如图所示,函数的平均变化率的几何意义是:直线AB的斜率。
事实上,。
换一种表述:
曲线上一点及其附近一点,
经过点、作曲线的割线,
则有。
要点诠释:根据平均变化率的几何意义,可求解有关曲线割线的斜率。
2.导数的几何意义——曲线的切线
如图1,当沿着曲线趋近于点时,割线的变化趋势是什么?
我们发现,当点沿着曲线无限接近点P即Δx→0时,割线趋近于确定的位置,这个确定位置的直线PT称为曲线在点P处的切线.
定义:如右图,当点沿曲线无限接近于点,
即时,割线的极限位置直线叫做曲线在点处的切线。 T
也就是:当时,割线斜率的极限,就是切线的斜率。
即:。
要点诠释:(1)曲线上一点切线的斜率值只与该点的位置有关。
(2)切线斜率的本质———函数在处的导数。
(3)曲线的切线的斜率的符号可以刻画函数的增减性。
①若曲线在点处的导数不存在,但有切线,则切线与轴垂直。
②,切线与轴正向夹角为锐角,瞬时递增;,切线与轴正向夹角为钝角,瞬时递减;,切线与轴零度角,瞬时无增减。
(4)曲线的切线可能和曲线有多个公共点;
为什么要用割线的极限位置来定义切线,而不说“与曲线只有一个公共点的直线叫做切线?”
过去我们定义圆的切线就是“与圆有且只有一个公共点的直线”,这个定义符合圆、椭圆等一类曲线,那么,能否对任何曲线C都用“与C有且只有一个公共点”来定义C的切线呢?如图1-1-2-1的曲线C是我们熟知的正弦曲线y=sin x的一部分,直线2显然与曲线C有唯一公共点M,但我们不能说直线2与曲线C相切;而直线1尽管与曲线C有不止一个公共点,但我们可以说直线1是曲线C在点N处的切线。
要点二、曲线的切线
(1)用导数的几何意义求曲线的切线方程的方法步骤:
①求出切点的坐标;
②求出函数在点处的导数
③得切线方程
(2)在点处的切线与过点(x0,y0)的切线的区别。
在点处的切线是说明点为此切线的切点;而过点(x0,y0)的切线,则强调切线是过点(x0,y0),此点可以是切点,也可以不是切点。因此在求过点(x0,y0)的切线方程时,先应判断点(x0,y0)是否为曲线上的点,若是则为第一类解法,若不同则必须先在曲线上取一切点,求过此切点的切线方程,再将点(x0,y0)代入,求得切点的坐标,进而求过点(x0,y0)的切线方程。
要点三、导数的概念
导函数定义:
由函数f(x)在x=x0处求导数的过程可以看到,当时, 是一个确定的数,那么,当x变化时,便是x的一个函数,我们叫它为f(x)的导函数.记作:或,
即:
要点诠释:
函数在点处的导数、导函数之间的区别与联系。
(1)函数在一点处的导数,就是在该点的函数的改变量与自变量的改变量之比的极限,它是一个常数,不是变数。
(2)函数的导数,是指某一区间内任一点x而言的,也就是函数f(x)的导函数。
(3)函数在点处的导数就是导函数在处的函数值。
导函数也简称导数,所以
所以求函数在一点处的导数,一般是先求出函数的导函数,再计算这点的导数函数值。
导函数求法:
由导数的定义可知,求函数的导数的一般方法是:
(1).求函数的改变量。
(2).求平均变化率。
(3).取极限,得导数=。
要点四、导数的定义的几种形式:
割线的极限即为切线,即为导数,从这个几何意义上看导数式可以有多种表达形式,如:
;(或:;;)
。
要点诠释:只要是时,极限式所表示的是割线的斜率(或其若干倍),就能表示为导数式。
【典型例题】
类型一、求曲线的切线方程
例1.曲线的方程为,那么求此曲线在点P(1,2)处的切线的斜率,以及切线的方程.
【解析】 利用导数的几何意义,曲线在点P(1,2)处的切线的斜率等于函数在处的导数值,再利用直线的点斜式方程写出切线方程.
由得,所以曲线在点处的切线斜率为,
过点P的切线方程为,即.
【总结升华】 求曲线上一点处切线的步骤:
①求函数y=f(x)在点处的导数,即曲线y=f(x)在处切线的斜率。
②由点斜式写出直线方程:;如果y=f(x)在的切线平行于y轴(此时导数不存在)时,由切线定义知:切线方程为:.
举一反三:
【变式1】(2018 西藏一模)已知曲线的一条切线的斜率为,则切点的横坐标为( )
A.1 B.2 C.3 D. 4
【答案】A
【解析】已知曲线的一条切线的斜率为,
,则切点的横坐标为1,故选A.
【变式2】已知:曲线上一点,求:点处的切线方程。
【答案】 对于函数,
,
,,
则点处的切线的斜率:,
切线方程:。
【变式3】(2018春 东港区校级期末)已知函数的图象在点处的切线方程是 ,则的值等于( )
A.1 B. C.3 D.0
【答案】
【解析】由已知点在切线上,所以,
切点处的导数为切线斜率,所以,
即,故选C。
例2.已知函数f(x)=x3-3x及y=f(x)上一点P(1,-2),过点P作直线l.
(1)求使直线l和y=f(x)相切且以P为切点的直线方程;
(2)求使直线l和y=f(x)相切且切点异于点P的直线方程y=g(x).
【解析】 (1)y′==3x2-3.
则过点P且以P(1,-2)为切点的直线的斜率
k1=f′(1)=0,
∴所求直线方程为y=-2.
(2)设切点坐标为(x0,-3x0),
则直线l的斜率k2=f′(x0)=3-3,
∴直线l的方程为y-(-3x0)=(3-3)(x-x0)
又直线l过点P(1,-2),
∴-2-(-3x0)=(3-3)(1-x0),
∴-3x0+2=(3-3)(x0-1),
解得x0=1(舍去)或x0=-.
故所求直线斜率k=3-3=-,
于是:y-(-2)=- (x-1),即y=-x+.
【总结升华】 求曲线的切线时,要注意区分不同的说法:通常情况下,求曲线在某点处的切线时,该点即为切点;求曲线经过某点的切线时,该点不一定是切点。同时本题也说明了曲线的切线与曲线可能有超过一个以上的公共点.
举一反三:
【变式1】 求曲线经过点的切线方程.
【解析】 本题要分点是切点和不是切点两类进行求解.
若点是切点,由得,则,于是切线方程为,即;
若点不是切点,设切点为:则切线率,所以
解之得,所以,所以切线方程是,即.
【变式2】已知曲线。
(1)求曲线过点A(1,0)的切线方程;
(2)求满足斜率为的曲线的切线方程。
【答案】(1)设过点A(1,0)的切线的切点坐标为,因为,所以该切线的斜率为,切线方程为。 ①
将A(1,0)代入①式,得。所以所求的切线方程为y=―4x+4。
(2)设切点坐标为,由(1)知,切线的斜率为,则,。那么切点为或。
所以所求的切线方程为或。
【变式3】 已知直线l1为曲线y=x2+x-2在点(1,0)处的切线,l2为该曲线的另一条切线,且l1⊥l2.
(1)求直线l2的方程;
(2)求由直线l1、l2和x轴所围成的三角形的面积.
【答案】
(1)y′|x=1
所以l1的方程为:y=3(x-1),即y=3x-3.
设l2过曲线y=x2+x-2上的点B(b,b2+b-2),
y′|x=b2b+1,
所以l2的方程为:y-(b2+b-2)=(2b+1)·(x-b),即y=(2b+1)x-b2-2.
因为l1⊥l2,所以3×(2b+1)=-1,所以b=-,所以l2的方程为:.
(2)由得
即l1与l2的交点坐标为.
又l1,l2与x轴交点坐标分别为(1,0),
所以所求三角形面积.
类型二、利用定义求导函数
例3.已知,求,
【解析】 因为,所以
。
当Δx→0时,,当x=2时,。
【总结升华】求导数的步骤和求导数值的步骤一样,叫三步法求导。
举一反三:
【变式1】求函数在内的导函数。
【答案】,
【变式2】求函数在x=2处的导数。
[解析] 解法一:(导数定义法)
∵,
∴。
∴。
解法二:(导函数的函数值法)
∵,
∴。
∴。
∴。
类型三、导数的几种形式
例4. 若,则________。
【解析】 根据导数定义:
(这时Δ=-k),
所以
。
【总结升华】
(1)有一种错误的解法:
根据导数的定义:(这时Δx=k),
所以 。
(2)在导数的定义中,增量Δx的形式是多种多样的,但不论Δx选择哪种形式,Δy也必须选择与之相对应的形式。利用函数在x=x0处可导的条件,可以将已给定的极限式恒等变形为导数定义的形式。概念是解决问题的重要依据,只有熟练掌握概念的本质属性,把握其内涵与外延,才能灵活地应用概念进行解题。
举一反三:
【变式1】 函数满足,则当x无限趋近于0时,
(1)
(2)
【答案】(1)
(2)
【变式2】. 若
(1)求的值。(2)求的值。
【答案】
【变式3】设函数在点x0处可导,则________。
【答案】 原式
。
【巩固练习】
选择题
1.一个物体的运动方程为其中的单位是米,的单位是秒,
那么物体在秒末的瞬时速度是( )
A.米/秒 B.米/秒
C.米/秒 D.米/秒
2.(2018 东昌府区校级二模)若点P在曲线 上移动,经过点P的切线的倾斜角为 ,则角 的取值范围是( )
A. B.
C. D.
3. 函数在处的导数的几何意义是( )
A 在点处的函数值
B 在点处的切线与轴所夹锐角的正切值
C 曲线在点处的切线的斜率
D 点与点(0,0)连线的斜率.
4.(2018春 湖北校级期末)已知函数y=3x4+a,y=4x3,若它们的图象有公共点,且在公共点处的切线重合,则切斜线率为( )
A.0 B.12 C.0或12 D.4或1
5.已知函数的切线的斜率等于1,则其切线方程有( )
A.1条 B.2条 C.多于2条 D.不确定
6.(2018 上饶三模)定义:如果函数在[a,b]上存在x1,x2(a<x1<x2<b)满足,,则称函数在[a,b]上的“双中值函数”。已知函数是[0,a]上的“双中值函数”,则实数a的取值范围是( )
A. B. C. D.
填空题
7.曲线在点处的切线方程为3x+y+3=0,则________0。(填“>”“<”“=”“≥”或“≤”)
8.已知曲线y=x2-2上一点P(1,-),则过点P的切线的倾斜角为________.
9.已知函数在x=x0处的导数为11,则________。
10.在曲线的切线中,斜率最小的切线的方程为________。
11.若抛物线y=x2―x+c上一点P的横坐标是―2,抛物线过点P的切线恰好过坐标原点,则c的值为________。
解答题
12.已知s=,求t=3秒时的瞬时速度。
13.如果曲线y=x2+x―3的某一条切线与直线y=3x+4平行,求切点坐标与切线方程。
14.曲线上有两点A(4,0)、B(2,4)。求:
(1)割线AB的斜率kAB及AB所在直线的方程;
(2)在曲线上是否存在点C,使过C点的切线与AB所在直线平行?若存在,求出C点的坐标及切线方程;若不存在,请说明理由。
15.已知函数f(x)=x3-3x及y=f(x)上一点P(1,-2),过点P作直线l.
(1)求使直线l和y=f(x)相切且以P为切点的直线方程;
(2)求使直线l和y=f(x)相切且切点异于点P的直线方程y=g(x).
【答案与解析】
1.【答案】C
【解析】有定义可求得
2. 【答案】 B
【解析】 函数的导数 ,
,又 ,
或,故选B。
3. 【答案】 C
【解析】 依据定义既能做出正确判断。
4.【答案】C
【解析】设公共点为P(x0,y0),则在函数y=3x4+a中,
,
则在P点处的切线方程为
即
化简得:
在函数y=4x3中,
则在P点处的切线方程为
即
化简得,
又两个函数在公共点处的切线重合,
∴
∴ 或
∴切线斜率为0或12。
5.【答案】 B
【解析】 由定义求得y'=3x2,设切点为,由,得,即在点和点处有斜率为1的切线,故有两条。
6.【答案】C
【解析】由题意可知,∵,
在区间[0,a]存在x1,x2,(a<x1<x2<b),
满足,
∵,
∴,
∴方程3x2―2x=a2―a在区间(0,a)有两个不相等的解。
令,(0<x<a)
则,
解得:。
∴实数a的取值范围是
故选:C
7.【答案】 <
【解析】 由题知就是切线方程的斜率,即,故。
8.【答案】 45°
【解析】∵y=x2-2,∴y′
∴y′|x=1=1.∴点P(1,-)处的切线的斜率为1,则切线的倾斜角为45°.
9.【答案】 -11
【解析】 ∵,
∴
10.【答案】 3x-y-11=0
【解析】 由导数的定义知y'=3x2+6x+6=3(x2+2x+1)+3=3(x+1)2+3,所以
当x=-1时,斜率有最小值为3。又因为当x=-1时,y=-14,
所以切线方程为y+14=3(x+1),即y=3x-11。
11.【答案】 4
【解析】 ∵y'=2x-1,∴。又P(-2,6+c),∴,∴c=4。
12.【解析】由题意可知某段时间内的平均速度随变化而变化,越小,越接近于一个定值,由极限定义可知,这个值就是时,的极限。
V===(6+=3g=29.4(米/秒)。
13.【解析】 ∵切线与直线y=3x+4平行,
∴切线的斜率为3。
设切点坐标为(x0,y0),则。
又
。
当Δx→0时,,
∴2x0+1=3从而x0=1。
代入得y0=-1。
∴切点坐标为(1,―1)。
切线方程为y+1=3(x―1),即3x―y―4=0。
14.【解析】 (1)∵,
∴割线AB所在直线方程是y=―2(x―4),
即2x+y―8=0。
(2)由导数定义可知y'=―2x+4,―2x+4=―2,
∴x=3,y=-32+3×4=3。
∴在曲线上存在点C,使过C点的切线与AB所在直线平行,C点坐标为(3,3),
所求切线方程为2x+y-9=0。
15. 【解析】 (1)
则过点P且以P(1,-2)为切点的直线的斜率
,
∴所求直线方程为y=-2.
(2)设切点坐标为,
则直线l的斜率
∴直线l的方程为
又直线l过点P(1,-2),
∴
∴
解得x0=1(舍去)或.
故所求直线斜率,
于是:,即。
【学习目标】
1.理解导数的几何意义。
2.理解导数的全面涵义。
3.掌握利用导数求函数图象的切线的斜率。
4.会求过点(或在点处)的切线方程。
【要点梳理】(根据课标要求进行适当的深化与拓展。)
要点一、导数几何意义
平均变化率的几何意义——曲线的割线
函数的平均变化率的几何意义是表示连接函数图像上两点割线的斜率。
如图所示,函数的平均变化率的几何意义是:直线AB的斜率。
事实上,。
换一种表述:
曲线上一点及其附近一点,
经过点、作曲线的割线,
则有。
要点诠释:根据平均变化率的几何意义,可求解有关曲线割线的斜率。
2.导数的几何意义——曲线的切线
如图1,当沿着曲线趋近于点时,割线的变化趋势是什么?
我们发现,当点沿着曲线无限接近点P即Δx→0时,割线趋近于确定的位置,这个确定位置的直线PT称为曲线在点P处的切线.
定义:如右图,当点沿曲线无限接近于点,
即时,割线的极限位置直线叫做曲线在点处的切线。 T
也就是:当时,割线斜率的极限,就是切线的斜率。
即:。
要点诠释:(1)曲线上一点切线的斜率值只与该点的位置有关。
(2)切线斜率的本质———函数在处的导数。
(3)曲线的切线的斜率的符号可以刻画函数的增减性。
①若曲线在点处的导数不存在,但有切线,则切线与轴垂直。
②,切线与轴正向夹角为锐角,瞬时递增;,切线与轴正向夹角为钝角,瞬时递减;,切线与轴零度角,瞬时无增减。
(4)曲线的切线可能和曲线有多个公共点;
为什么要用割线的极限位置来定义切线,而不说“与曲线只有一个公共点的直线叫做切线?”
过去我们定义圆的切线就是“与圆有且只有一个公共点的直线”,这个定义符合圆、椭圆等一类曲线,那么,能否对任何曲线C都用“与C有且只有一个公共点”来定义C的切线呢?如图1-1-2-1的曲线C是我们熟知的正弦曲线y=sin x的一部分,直线2显然与曲线C有唯一公共点M,但我们不能说直线2与曲线C相切;而直线1尽管与曲线C有不止一个公共点,但我们可以说直线1是曲线C在点N处的切线。
要点二、曲线的切线
(1)用导数的几何意义求曲线的切线方程的方法步骤:
①求出切点的坐标;
②求出函数在点处的导数
③得切线方程
(2)在点处的切线与过点(x0,y0)的切线的区别。
在点处的切线是说明点为此切线的切点;而过点(x0,y0)的切线,则强调切线是过点(x0,y0),此点可以是切点,也可以不是切点。因此在求过点(x0,y0)的切线方程时,先应判断点(x0,y0)是否为曲线上的点,若是则为第一类解法,若不同则必须先在曲线上取一切点,求过此切点的切线方程,再将点(x0,y0)代入,求得切点的坐标,进而求过点(x0,y0)的切线方程。
要点三、导数的概念
导函数定义:
由函数f(x)在x=x0处求导数的过程可以看到,当时, 是一个确定的数,那么,当x变化时,便是x的一个函数,我们叫它为f(x)的导函数.记作:或,
即:
要点诠释:
函数在点处的导数、导函数之间的区别与联系。
(1)函数在一点处的导数,就是在该点的函数的改变量与自变量的改变量之比的极限,它是一个常数,不是变数。
(2)函数的导数,是指某一区间内任一点x而言的,也就是函数f(x)的导函数。
(3)函数在点处的导数就是导函数在处的函数值。
导函数也简称导数,所以
所以求函数在一点处的导数,一般是先求出函数的导函数,再计算这点的导数函数值。
导函数求法:
由导数的定义可知,求函数的导数的一般方法是:
(1).求函数的改变量。
(2).求平均变化率。
(3).取极限,得导数=。
要点四、导数的定义的几种形式:
割线的极限即为切线,即为导数,从这个几何意义上看导数式可以有多种表达形式,如:
;(或:;;)
。
要点诠释:只要是时,极限式所表示的是割线的斜率(或其若干倍),就能表示为导数式。
【典型例题】
类型一、求曲线的切线方程
例1.曲线的方程为,那么求此曲线在点P(1,2)处的切线的斜率,以及切线的方程.
【解析】 利用导数的几何意义,曲线在点P(1,2)处的切线的斜率等于函数在处的导数值,再利用直线的点斜式方程写出切线方程.
由得,所以曲线在点处的切线斜率为,
过点P的切线方程为,即.
【总结升华】 求曲线上一点处切线的步骤:
①求函数y=f(x)在点处的导数,即曲线y=f(x)在处切线的斜率。
②由点斜式写出直线方程:;如果y=f(x)在的切线平行于y轴(此时导数不存在)时,由切线定义知:切线方程为:.
举一反三:
【变式1】(2018 西藏一模)已知曲线的一条切线的斜率为,则切点的横坐标为( )
A.1 B.2 C.3 D. 4
【答案】A
【解析】已知曲线的一条切线的斜率为,
,则切点的横坐标为1,故选A.
【变式2】已知:曲线上一点,求:点处的切线方程。
【答案】 对于函数,
,
,,
则点处的切线的斜率:,
切线方程:。
【变式3】(2018春 东港区校级期末)已知函数的图象在点处的切线方程是 ,则的值等于( )
A.1 B. C.3 D.0
【答案】
【解析】由已知点在切线上,所以,
切点处的导数为切线斜率,所以,
即,故选C。
例2.已知函数f(x)=x3-3x及y=f(x)上一点P(1,-2),过点P作直线l.
(1)求使直线l和y=f(x)相切且以P为切点的直线方程;
(2)求使直线l和y=f(x)相切且切点异于点P的直线方程y=g(x).
【解析】 (1)y′==3x2-3.
则过点P且以P(1,-2)为切点的直线的斜率
k1=f′(1)=0,
∴所求直线方程为y=-2.
(2)设切点坐标为(x0,-3x0),
则直线l的斜率k2=f′(x0)=3-3,
∴直线l的方程为y-(-3x0)=(3-3)(x-x0)
又直线l过点P(1,-2),
∴-2-(-3x0)=(3-3)(1-x0),
∴-3x0+2=(3-3)(x0-1),
解得x0=1(舍去)或x0=-.
故所求直线斜率k=3-3=-,
于是:y-(-2)=- (x-1),即y=-x+.
【总结升华】 求曲线的切线时,要注意区分不同的说法:通常情况下,求曲线在某点处的切线时,该点即为切点;求曲线经过某点的切线时,该点不一定是切点。同时本题也说明了曲线的切线与曲线可能有超过一个以上的公共点.
举一反三:
【变式1】 求曲线经过点的切线方程.
【解析】 本题要分点是切点和不是切点两类进行求解.
若点是切点,由得,则,于是切线方程为,即;
若点不是切点,设切点为:则切线率,所以
解之得,所以,所以切线方程是,即.
【变式2】已知曲线。
(1)求曲线过点A(1,0)的切线方程;
(2)求满足斜率为的曲线的切线方程。
【答案】(1)设过点A(1,0)的切线的切点坐标为,因为,所以该切线的斜率为,切线方程为。 ①
将A(1,0)代入①式,得。所以所求的切线方程为y=―4x+4。
(2)设切点坐标为,由(1)知,切线的斜率为,则,。那么切点为或。
所以所求的切线方程为或。
【变式3】 已知直线l1为曲线y=x2+x-2在点(1,0)处的切线,l2为该曲线的另一条切线,且l1⊥l2.
(1)求直线l2的方程;
(2)求由直线l1、l2和x轴所围成的三角形的面积.
【答案】
(1)y′|x=1
所以l1的方程为:y=3(x-1),即y=3x-3.
设l2过曲线y=x2+x-2上的点B(b,b2+b-2),
y′|x=b2b+1,
所以l2的方程为:y-(b2+b-2)=(2b+1)·(x-b),即y=(2b+1)x-b2-2.
因为l1⊥l2,所以3×(2b+1)=-1,所以b=-,所以l2的方程为:.
(2)由得
即l1与l2的交点坐标为.
又l1,l2与x轴交点坐标分别为(1,0),
所以所求三角形面积.
类型二、利用定义求导函数
例3.已知,求,
【解析】 因为,所以
。
当Δx→0时,,当x=2时,。
【总结升华】求导数的步骤和求导数值的步骤一样,叫三步法求导。
举一反三:
【变式1】求函数在内的导函数。
【答案】,
【变式2】求函数在x=2处的导数。
[解析] 解法一:(导数定义法)
∵,
∴。
∴。
解法二:(导函数的函数值法)
∵,
∴。
∴。
∴。
类型三、导数的几种形式
例4. 若,则________。
【解析】 根据导数定义:
(这时Δ=-k),
所以
。
【总结升华】
(1)有一种错误的解法:
根据导数的定义:(这时Δx=k),
所以 。
(2)在导数的定义中,增量Δx的形式是多种多样的,但不论Δx选择哪种形式,Δy也必须选择与之相对应的形式。利用函数在x=x0处可导的条件,可以将已给定的极限式恒等变形为导数定义的形式。概念是解决问题的重要依据,只有熟练掌握概念的本质属性,把握其内涵与外延,才能灵活地应用概念进行解题。
举一反三:
【变式1】 函数满足,则当x无限趋近于0时,
(1)
(2)
【答案】(1)
(2)
【变式2】. 若
(1)求的值。(2)求的值。
【答案】
【变式3】设函数在点x0处可导,则________。
【答案】 原式
。
【巩固练习】
选择题
1.一个物体的运动方程为其中的单位是米,的单位是秒,
那么物体在秒末的瞬时速度是( )
A.米/秒 B.米/秒
C.米/秒 D.米/秒
2.(2018 东昌府区校级二模)若点P在曲线 上移动,经过点P的切线的倾斜角为 ,则角 的取值范围是( )
A. B.
C. D.
3. 函数在处的导数的几何意义是( )
A 在点处的函数值
B 在点处的切线与轴所夹锐角的正切值
C 曲线在点处的切线的斜率
D 点与点(0,0)连线的斜率.
4.(2018春 湖北校级期末)已知函数y=3x4+a,y=4x3,若它们的图象有公共点,且在公共点处的切线重合,则切斜线率为( )
A.0 B.12 C.0或12 D.4或1
5.已知函数的切线的斜率等于1,则其切线方程有( )
A.1条 B.2条 C.多于2条 D.不确定
6.(2018 上饶三模)定义:如果函数在[a,b]上存在x1,x2(a<x1<x2<b)满足,,则称函数在[a,b]上的“双中值函数”。已知函数是[0,a]上的“双中值函数”,则实数a的取值范围是( )
A. B. C. D.
填空题
7.曲线在点处的切线方程为3x+y+3=0,则________0。(填“>”“<”“=”“≥”或“≤”)
8.已知曲线y=x2-2上一点P(1,-),则过点P的切线的倾斜角为________.
9.已知函数在x=x0处的导数为11,则________。
10.在曲线的切线中,斜率最小的切线的方程为________。
11.若抛物线y=x2―x+c上一点P的横坐标是―2,抛物线过点P的切线恰好过坐标原点,则c的值为________。
解答题
12.已知s=,求t=3秒时的瞬时速度。
13.如果曲线y=x2+x―3的某一条切线与直线y=3x+4平行,求切点坐标与切线方程。
14.曲线上有两点A(4,0)、B(2,4)。求:
(1)割线AB的斜率kAB及AB所在直线的方程;
(2)在曲线上是否存在点C,使过C点的切线与AB所在直线平行?若存在,求出C点的坐标及切线方程;若不存在,请说明理由。
15.已知函数f(x)=x3-3x及y=f(x)上一点P(1,-2),过点P作直线l.
(1)求使直线l和y=f(x)相切且以P为切点的直线方程;
(2)求使直线l和y=f(x)相切且切点异于点P的直线方程y=g(x).
【答案与解析】
1.【答案】C
【解析】有定义可求得
2. 【答案】 B
【解析】 函数的导数 ,
,又 ,
或,故选B。
3. 【答案】 C
【解析】 依据定义既能做出正确判断。
4.【答案】C
【解析】设公共点为P(x0,y0),则在函数y=3x4+a中,
,
则在P点处的切线方程为
即
化简得:
在函数y=4x3中,
则在P点处的切线方程为
即
化简得,
又两个函数在公共点处的切线重合,
∴
∴ 或
∴切线斜率为0或12。
5.【答案】 B
【解析】 由定义求得y'=3x2,设切点为,由,得,即在点和点处有斜率为1的切线,故有两条。
6.【答案】C
【解析】由题意可知,∵,
在区间[0,a]存在x1,x2,(a<x1<x2<b),
满足,
∵,
∴,
∴方程3x2―2x=a2―a在区间(0,a)有两个不相等的解。
令,(0<x<a)
则,
解得:。
∴实数a的取值范围是
故选:C
7.【答案】 <
【解析】 由题知就是切线方程的斜率,即,故。
8.【答案】 45°
【解析】∵y=x2-2,∴y′
∴y′|x=1=1.∴点P(1,-)处的切线的斜率为1,则切线的倾斜角为45°.
9.【答案】 -11
【解析】 ∵,
∴
10.【答案】 3x-y-11=0
【解析】 由导数的定义知y'=3x2+6x+6=3(x2+2x+1)+3=3(x+1)2+3,所以
当x=-1时,斜率有最小值为3。又因为当x=-1时,y=-14,
所以切线方程为y+14=3(x+1),即y=3x-11。
11.【答案】 4
【解析】 ∵y'=2x-1,∴。又P(-2,6+c),∴,∴c=4。
12.【解析】由题意可知某段时间内的平均速度随变化而变化,越小,越接近于一个定值,由极限定义可知,这个值就是时,的极限。
V===(6+=3g=29.4(米/秒)。
13.【解析】 ∵切线与直线y=3x+4平行,
∴切线的斜率为3。
设切点坐标为(x0,y0),则。
又
。
当Δx→0时,,
∴2x0+1=3从而x0=1。
代入得y0=-1。
∴切点坐标为(1,―1)。
切线方程为y+1=3(x―1),即3x―y―4=0。
14.【解析】 (1)∵,
∴割线AB所在直线方程是y=―2(x―4),
即2x+y―8=0。
(2)由导数定义可知y'=―2x+4,―2x+4=―2,
∴x=3,y=-32+3×4=3。
∴在曲线上存在点C,使过C点的切线与AB所在直线平行,C点坐标为(3,3),
所求切线方程为2x+y-9=0。
15. 【解析】 (1)
则过点P且以P(1,-2)为切点的直线的斜率
,
∴所求直线方程为y=-2.
(2)设切点坐标为,
则直线l的斜率
∴直线l的方程为
又直线l过点P(1,-2),
∴
∴
解得x0=1(舍去)或.
故所求直线斜率,
于是:,即。
