人教版高中数学理科选修2-2同步练习题、期中、期末复习资料、补习资料:11定积分的概念
文档属性
| 名称 | 人教版高中数学理科选修2-2同步练习题、期中、期末复习资料、补习资料:11定积分的概念 |

|
|
| 格式 | zip | ||
| 文件大小 | 611.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-21 09:47:21 | ||
图片预览




文档简介
定积分的概念
【学习目标】
1.通过求曲边梯形的面积和汽车行驶的路程,了解定积分的背景;
2.借助于几何直观定积分的基本思想,了解定积分的概念,能用定积分定义求简单的定积分;
3.理解掌握定积分的几何意义.
【要点梳理】
要点一、定积分的定义
定积分的概念
一般地,设函数在区间上连续,用分点
将区间等分成个小区间,每个小区间长度为(),在每个小区间上任取一点,作和式:
如果无限接近于(亦即)时,上述和式无限趋近于常数,那么称该常数为函数在区间上的定积分。记为:,
定积分的相关名称:
——叫做积分号,
——叫做被积函数,
——叫做被积表达式,
x——叫做积分变量,
a——叫做积分下限,
b——叫做积分上限,
[a,b]——叫做积分区间。
要点诠释:
(1)定积分是一个常数,即无限趋近的常数(时)
记为,而不是.
(2) 定积分是一个数值(极限值),它的值仅仅取决于被积函数与积分的上、下限,而与积分变量用什么字母表示无关,即(称为积分形式的不变性),另外定积分与积分区间[a,b]息息相关,不同的积分区间,定积分的积分上下限不同,所得的值也就不同,例如与的值就不同。
(3)用定义求定积分的一般方法是:
①分割:等分区间;
②近似代替:取点;
③求和:;
④取极限:
(4)按定积分的定义,
① 由连续曲线、直线x=a、x=b及x轴所围成的曲边梯形的面积为;
② 设物体运动的速度v=v(t),则此物体在时间区间[a,b]内运动的距离s为。
要点二、定积分的几何意义
定积分的几何意义:
从几何上看,如果在区间上函数连续且恒有,那么定积分表示由直线和曲线所围成的曲边梯形(如图中的阴影部分)的面积,这就是定积分的几何意义。
一般情况下,定积分的几何意义是介于轴、函数的图形以及直线之间各部分面积的代数和,在轴上方的面积取正号,在轴下方的面积取负号。
要点诠释:
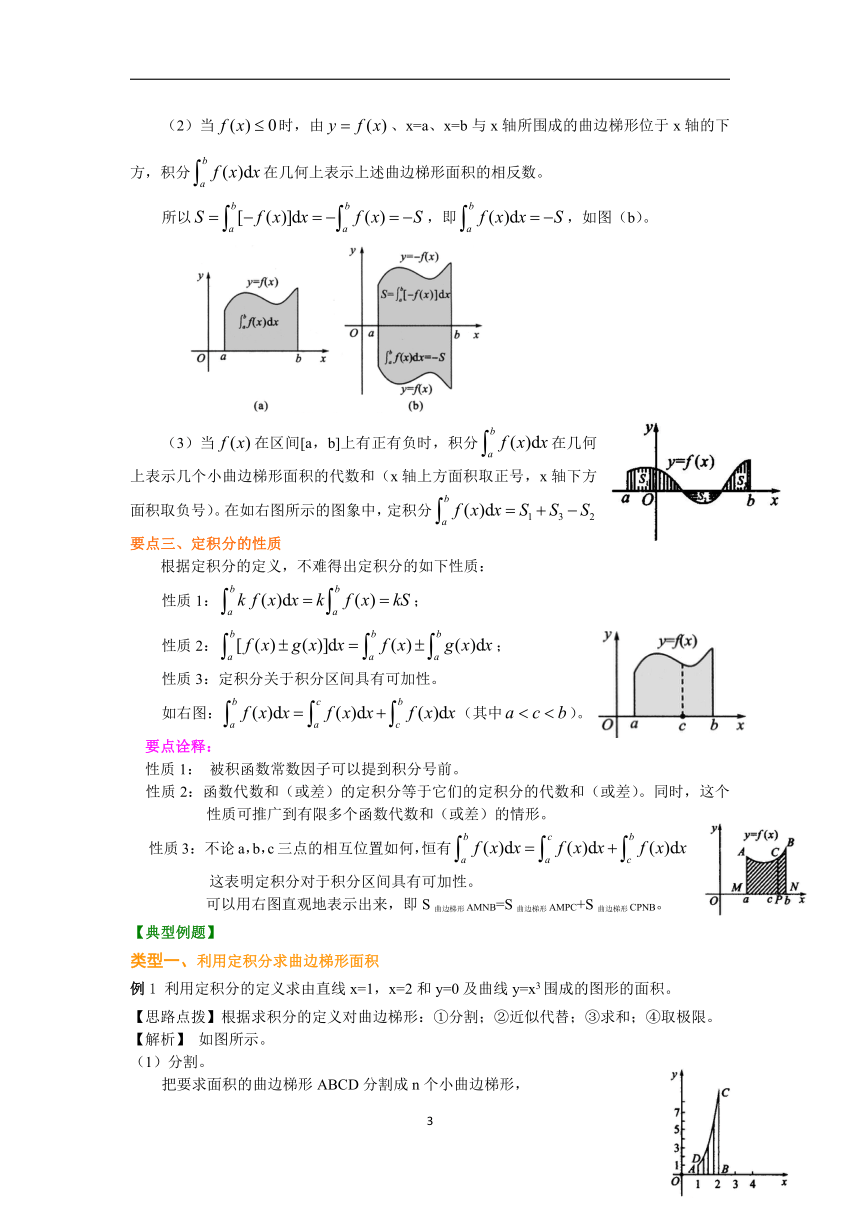
(1)当时,积分在几何上表示由、x=a、x=b与x轴所围成的曲边梯形的面积;特别地:当a=b时,有,如图(a)。
(2)当时,由、x=a、x=b与x轴所围成的曲边梯形位于x轴的下方,积分在几何上表示上述曲边梯形面积的相反数。
所以,即,如图(b)。
(3)当在区间[a,b]上有正有负时,积分在几何上表示几个小曲边梯形面积的代数和(x轴上方面积取正号,x轴下方面积取负号)。在如右图所示的图象中,定积分。
要点三、定积分的性质
根据定积分的定义,不难得出定积分的如下性质:
性质1:;
性质2:;
性质3:定积分关于积分区间具有可加性。
如右图:(其中)。
要点诠释:
性质1: 被积函数常数因子可以提到积分号前。
性质2:函数代数和(或差)的定积分等于它们的定积分的代数和(或差)。同时,这个性质可推广到有限多个函数代数和(或差)的情形。
性质3: 不论a,b,c三点的相互位置如何,恒有。这表明定积分对于积分区间具有可加性。
可以用右图直观地表示出来,即S曲边梯形AMNB=S曲边梯形AMPC+S曲边梯形CPNB。
【典型例题】
类型一、利用定积分求曲边梯形面积
例1 利用定积分的定义求由直线x=1,x=2和y=0及曲线y=x3围成的图形的面积。
【思路点拨】根据求积分的定义对曲边梯形:①分割;②近似代替;③求和;④取极限。
【解析】 如图所示。
(1)分割。
把要求面积的曲边梯形ABCD分割成n个小曲边梯形,
用分点, ,…,把区间[1,2]等分成n个小区间,
,,…,,…,, 每个小区间的长度为,过各分点作x轴的垂线,把曲边梯形ABCD分割成n个小曲边梯形,它们的面积分别记作ΔS1,ΔS2,…,ΔSn。
(2)近似代替。
取各小区间的左端点,用以点的纵坐标为一边,以小区间长为其邻边的小矩形面积近似代替第i个小曲边梯形的面积,可以近似地表示为:(i=1,2,3,…,n)。
因为每一个小矩形的面积都可以作为相应的小曲边梯形面积的近似值,所以n个小矩形面积的和就是曲边梯形ABCD面积S的近似值,即 ①。
(3)求和。
当分点数目愈多,即Δx愈小时,和式①的值就愈接近曲边梯形ABCD的面积S。因此,n→+∞即Δx→0时,和式①的极限就是所求的曲边梯形ABCD的面积。因为:
。
(4)取极限。
。
【总结升华】
(1)根据定义求曲边梯形面积的步骤:
①分割;②近似代替;③求和;④取极限。
(2)求和时首先可提取公因式,再将和式进行处理。
(3)从图形上看,当n越来越大时,划分越来越细,阴影部分的面积与曲边梯形的面积相差越来越小;当n→+∞时,小矩形组成部分近似于曲边梯形,因此可以将视为直线x=1、x=2、y=0和曲线y=x3围成的图形的面积。
举一反三:
【变式】求由y=3x、x=0、x=1、y=0围成的图形的面积S。
【答案】(1)分割
把区间[0,1]等分成n个小区间:(i=1,2,…,n)。每个小区间长度为,把梯形分成n个小梯形,其面积记为ΔSi(i=1,2,…,n)。
(2)近似代替
用小矩形面积近似代替小梯形面积。
(i=1,2,…,n)。
(3)求和
。
(4)取极限
当n趋向于+∞时,趋近于,∴所求图形的面积S为。
类型二、利用定积分定义求运动物体的路程
例2 汽车以速度v做匀速直线运动时,经过时间t所行驶的路程为s=vt。如果汽车做变速直线运动,在时刻t的速度为v (t)=-t2+2(单元:km / h),那么它在0≤t≤1(单位:h)这段时间内行驶的路程s(单位:km)是多少?
【思路点拨】首先准确理解题意:所求路程就是速度在0≤t≤1上的积分。
【解析】
(1)分割
在时间区间[0,1]上等间隔地插入n-1外小分点,将它等分成n个小区间:
,,…,,记第i个区间为(i=1,2,…,n),其长度为,把汽车在时间段,,…,上行驶的路程分别记作:Δs1,Δs2,…,Δsn,则显然有。
(2)近似代替:
当n很大,即Δt很小时,在区间上,函数v(t)=-t2+2的值变化很小,近似地等于一个常数,不妨认为它近似地等于左端点处的函数。从物理意义上看,就是汽车在时间段(i=1,2,…,n)上速度的变化很小,不妨认为它近似地以时刻处的速度做匀速行驶,即在局部小范围内“以匀速代变速”,于是
(i=1,2,…,n) ①。
(3)求和:由①得
。
(4)取极限:
,所以这段时间内行驶的路程s是km。
【总结升华】 用分割、近似代替、求和、取极限这四个步骤可以求曲边多边形的面积,它体现了一种化整(分割)为零,积零为整(逼近)的思想方法。
举一反三:
【变式】 已知某运动物体做变速直线运动,它的速度v是时间t的函数v(t),写出物体在t=0到t=t0这段时间内所经过的路程s的求法。
【答案】
(1)分割
将时间区间[0,t0]分成n等份:
(i=1,2,…,n),
每个小区间所表示的时间为,
各小区间物体运动的路程记作Δsi(i=1,2,…,n)。
(2)近似代替
在每个小区间上以匀速直线运动的路程近似代替变速直线运动的路程:
在小区间上任取一时刻(i=1,2,…,n)。用时刻的速度近似代替第i个小区间上的速度。由匀速直线运动的路程公式,每个小区间物体运动所经过的路程可以近似地表示为
(i=1,2,…,n)。
(3)求和
因为每个小区间上物体运动的路程可以用这一区间上做匀速直线运动的路程近似代替,所以在时间[0,t0]范围物体运动的路程s,就可以用这一物体分别在n个小区间上做n个匀速直线运动的路程和近似代替。
即。 ①
(4)取极限
当所分时间区间愈短,即愈小时,和式①的值就愈接近s。因此,当n趋向于+∞,即趋向于0时,和式①无限趋近于s,所以s就是所求的物体在时间区间[0,t0]上所经过的路程。
类型三、定积分的几何意义
例3. 用定积分的几何意义求:
(1);
(2);
(3)。
【思路点拨】画出简图,结合图形确定积分区间。
【解析】(1)如下图:
阴影部分面积为,
从而。
(2)如右上图:
由于A的面积等于B的面积,
从而。
(3)设,则,表示半径为2的个圆,
由定积分的概念可知,表示如图所示的以2为半径的圆的面积,
所以
【总结升华】
(1)利用定积分的几何意义正确画出图形求定积分。
(2)表示曲边梯形的面积,而上半圆可看做特殊曲边梯形(有两边缩为点),这里面积易求,从而得出定积分的值。
举一反三:
【变式1】(2018 怀化二模)定积分的值为( )
A. B. C.π D.2π
【答案】∵,
∴(x-1)2+y2=1表示以(1,0)为圆心,以1为半径的圆,
∴定积分所围成的面积就是该圆的面积的四分之一,
∴定积分,
故选:A。
【变式2】利用定积分的几何定义求定积分:
(1); (2)
【答案】
(1)设,则表示个圆,
由定积分的概念可知,所求积分就是圆的面积,
所以
(2)设,则表示如图的曲边形,
其面积,
故.
【变式3】
已知甲、乙两车由同一起点同时出发,并沿同一路线(假定为直线)
行驶.甲车、乙车的速度曲线分别为和(如图所示).那么对
于图中给定的和,下列判断中一定正确的是( )
A. 在时刻,甲车在乙车前面
B. 时刻后,甲车在乙车后面
C. 在时刻,两车的位置相同
D. 时刻后,乙车在甲车前面
【答案】A
在时刻,显然甲的曲边图形的面积大于乙,所以甲车在前面,排除C、D; 在时刻,甲的曲边图形的面积明显大于乙,故选A.
类型四、定积分定义和性质的灵活运用
例4. 将和式表示为定积分。
【解析】 ∵
。
【总结升华】 将和式转化为积分形式的关键在于构造出定积分的定义结构,
即。
举一反三:
【变式】试将和式表示成定积分。
【答案】∵
。
例5.利用定积分的性质,用定积分表示曲线y=x―2,x=y2所围成的平面区域的面积。
【解析】如图所示,曲线所围成的平面区域的面积S=SA1+SA2,
A1:由,,x=1围成;
A2:由,y=x―2,x=1和x=4围成;
∴;。
∴。
【总结升华】 利用定积分求平面图形面积时,可按以下步骤进行:
①画图;②确定积分变量;③求交点,确定积分上、下限;④求定积分,得面积。
举一反三:
【变式1】
直线x=0,y=0,x=2与曲线所围所的图形的面积用定积分表示为________。
【答案】。
【变式2】 (2018 会宁县校级模拟)曲线与直线y=x―1及x=4所围成的封闭图形的面积用定积分表示为
【答案】令x=4,代入直线y=x-1得A(4,3),同理得
由,解得x=2,所以曲线与直线y=x-1交于点B(2,1)
∴SABC=S梯形ABEF-SBCEF
而
∵
∴封闭图形ABC的面积SABC=S梯形ABEF-SBCEF=4-。
【巩固练习】
一、选择题
1.等于( )
A.0 B.1 C. D.2
2.设连续函数,则当a<b时,定积分的符号( )
A.一定是正的
B.一定是负的
C.当0<a<b时是正的,当a<b<0时是负的
D.以上结论都不对
3.在求由x=a,x=b(a<b),及y=0围成的曲边梯形的面积S时,在区间[a,b]上等间隔地插入n―1个分点,分别过这些分点作x轴的垂线,把曲边梯形分成n个小曲边梯形,下列说法中正确的个数是( )
①n个小曲边梯形的面积和等于S;
②n个小曲边梯形的面积和小于S;
③n个小曲边梯形的面积和大于S;
④n个小曲边梯形的面积和与S之间的大小关系无法确定。
A.1 B.2 C.3 D.4
4.下列结论中错误的是( )
A.
B.
C.=+(其中
D.=
5.已知为偶函数且,则( )
A.0 B.4 C.8 D.16
6.(2018 陕西模拟)计算的结果是( )
A. B. C. D.
7.(2018春 唐山校级模拟)将和式的极限(P>0)表示成定积分为( )
A. B. C. D.
二、填空题
8.(2018 历下区校级四模改编)由曲线,直线y=x-2及y轴所围成的图形的面积用定积分表示为________。
9.若,则________。
10.若,,则________。
11.若,则由x=0,x=π,及x轴围成的图形的面积为________。
12.________。
三、解答题
13.计算定积分的值。
14.比较与的大小。
15.物体在力F的作用下从静止开始运动,力F的大小位移s(m)的关系是:,求物体运动5 m的过程中力F所做的功。
【答案与解析】
1.【答案】B
【解析】 ∵,故选B。
2.【答案】A
【解析】 由定积分的性质(4)可得,故选A。
3.【答案】A
【解析】 根据“化整为零”“积零为整”的思想知①是正确的,故选A。
4. 【答案】D.
【解析】依据定积分的性质可判断A、B、C是正确的,故选D。
5. 【答案】 D
【解析】为偶函数,则
6.【答案】C
【解析】
表示的几何意义是以(0,0)为圆心,2为半径第一象限内圆弧与坐标轴围成的
面积=,故选:C。
7.【答案】B
【解析】 ∵。
8.【答案】
【解析】如图所示:
联立 解得,∴M(4,2)。
由曲线,直线y=x-2及y轴所围成的图形的面积
。
9.【答案】6
【解析】 由定积分的定义可得。
10.【答案】5
【解析】 ∵。
11.【答案】2
【解析】 由正弦函数与余弦函数的图象,知,x∈[0,π]的图象与x轴围成的图形的面积等于,的图象与x轴围成的图形的面积的2倍,所以。
12.【答案】3
【解析】 ∵。
13.【解析】(―≤x≤0)的图象如右图所示:
所以。
14.【解析】∵,0≤sin x≤1,
∴sin5x≤sin x。
∴。
15.【解析】s∈[0,5],将[0,5]n等分,得,,
则,
在[si―1,si]的位移内,力Fi所做的功
,
所以
。
【学习目标】
1.通过求曲边梯形的面积和汽车行驶的路程,了解定积分的背景;
2.借助于几何直观定积分的基本思想,了解定积分的概念,能用定积分定义求简单的定积分;
3.理解掌握定积分的几何意义.
【要点梳理】
要点一、定积分的定义
定积分的概念
一般地,设函数在区间上连续,用分点
将区间等分成个小区间,每个小区间长度为(),在每个小区间上任取一点,作和式:
如果无限接近于(亦即)时,上述和式无限趋近于常数,那么称该常数为函数在区间上的定积分。记为:,
定积分的相关名称:
——叫做积分号,
——叫做被积函数,
——叫做被积表达式,
x——叫做积分变量,
a——叫做积分下限,
b——叫做积分上限,
[a,b]——叫做积分区间。
要点诠释:
(1)定积分是一个常数,即无限趋近的常数(时)
记为,而不是.
(2) 定积分是一个数值(极限值),它的值仅仅取决于被积函数与积分的上、下限,而与积分变量用什么字母表示无关,即(称为积分形式的不变性),另外定积分与积分区间[a,b]息息相关,不同的积分区间,定积分的积分上下限不同,所得的值也就不同,例如与的值就不同。
(3)用定义求定积分的一般方法是:
①分割:等分区间;
②近似代替:取点;
③求和:;
④取极限:
(4)按定积分的定义,
① 由连续曲线、直线x=a、x=b及x轴所围成的曲边梯形的面积为;
② 设物体运动的速度v=v(t),则此物体在时间区间[a,b]内运动的距离s为。
要点二、定积分的几何意义
定积分的几何意义:
从几何上看,如果在区间上函数连续且恒有,那么定积分表示由直线和曲线所围成的曲边梯形(如图中的阴影部分)的面积,这就是定积分的几何意义。
一般情况下,定积分的几何意义是介于轴、函数的图形以及直线之间各部分面积的代数和,在轴上方的面积取正号,在轴下方的面积取负号。
要点诠释:
(1)当时,积分在几何上表示由、x=a、x=b与x轴所围成的曲边梯形的面积;特别地:当a=b时,有,如图(a)。
(2)当时,由、x=a、x=b与x轴所围成的曲边梯形位于x轴的下方,积分在几何上表示上述曲边梯形面积的相反数。
所以,即,如图(b)。
(3)当在区间[a,b]上有正有负时,积分在几何上表示几个小曲边梯形面积的代数和(x轴上方面积取正号,x轴下方面积取负号)。在如右图所示的图象中,定积分。
要点三、定积分的性质
根据定积分的定义,不难得出定积分的如下性质:
性质1:;
性质2:;
性质3:定积分关于积分区间具有可加性。
如右图:(其中)。
要点诠释:
性质1: 被积函数常数因子可以提到积分号前。
性质2:函数代数和(或差)的定积分等于它们的定积分的代数和(或差)。同时,这个性质可推广到有限多个函数代数和(或差)的情形。
性质3: 不论a,b,c三点的相互位置如何,恒有。这表明定积分对于积分区间具有可加性。
可以用右图直观地表示出来,即S曲边梯形AMNB=S曲边梯形AMPC+S曲边梯形CPNB。
【典型例题】
类型一、利用定积分求曲边梯形面积
例1 利用定积分的定义求由直线x=1,x=2和y=0及曲线y=x3围成的图形的面积。
【思路点拨】根据求积分的定义对曲边梯形:①分割;②近似代替;③求和;④取极限。
【解析】 如图所示。
(1)分割。
把要求面积的曲边梯形ABCD分割成n个小曲边梯形,
用分点, ,…,把区间[1,2]等分成n个小区间,
,,…,,…,, 每个小区间的长度为,过各分点作x轴的垂线,把曲边梯形ABCD分割成n个小曲边梯形,它们的面积分别记作ΔS1,ΔS2,…,ΔSn。
(2)近似代替。
取各小区间的左端点,用以点的纵坐标为一边,以小区间长为其邻边的小矩形面积近似代替第i个小曲边梯形的面积,可以近似地表示为:(i=1,2,3,…,n)。
因为每一个小矩形的面积都可以作为相应的小曲边梯形面积的近似值,所以n个小矩形面积的和就是曲边梯形ABCD面积S的近似值,即 ①。
(3)求和。
当分点数目愈多,即Δx愈小时,和式①的值就愈接近曲边梯形ABCD的面积S。因此,n→+∞即Δx→0时,和式①的极限就是所求的曲边梯形ABCD的面积。因为:
。
(4)取极限。
。
【总结升华】
(1)根据定义求曲边梯形面积的步骤:
①分割;②近似代替;③求和;④取极限。
(2)求和时首先可提取公因式,再将和式进行处理。
(3)从图形上看,当n越来越大时,划分越来越细,阴影部分的面积与曲边梯形的面积相差越来越小;当n→+∞时,小矩形组成部分近似于曲边梯形,因此可以将视为直线x=1、x=2、y=0和曲线y=x3围成的图形的面积。
举一反三:
【变式】求由y=3x、x=0、x=1、y=0围成的图形的面积S。
【答案】(1)分割
把区间[0,1]等分成n个小区间:(i=1,2,…,n)。每个小区间长度为,把梯形分成n个小梯形,其面积记为ΔSi(i=1,2,…,n)。
(2)近似代替
用小矩形面积近似代替小梯形面积。
(i=1,2,…,n)。
(3)求和
。
(4)取极限
当n趋向于+∞时,趋近于,∴所求图形的面积S为。
类型二、利用定积分定义求运动物体的路程
例2 汽车以速度v做匀速直线运动时,经过时间t所行驶的路程为s=vt。如果汽车做变速直线运动,在时刻t的速度为v (t)=-t2+2(单元:km / h),那么它在0≤t≤1(单位:h)这段时间内行驶的路程s(单位:km)是多少?
【思路点拨】首先准确理解题意:所求路程就是速度在0≤t≤1上的积分。
【解析】
(1)分割
在时间区间[0,1]上等间隔地插入n-1外小分点,将它等分成n个小区间:
,,…,,记第i个区间为(i=1,2,…,n),其长度为,把汽车在时间段,,…,上行驶的路程分别记作:Δs1,Δs2,…,Δsn,则显然有。
(2)近似代替:
当n很大,即Δt很小时,在区间上,函数v(t)=-t2+2的值变化很小,近似地等于一个常数,不妨认为它近似地等于左端点处的函数。从物理意义上看,就是汽车在时间段(i=1,2,…,n)上速度的变化很小,不妨认为它近似地以时刻处的速度做匀速行驶,即在局部小范围内“以匀速代变速”,于是
(i=1,2,…,n) ①。
(3)求和:由①得
。
(4)取极限:
,所以这段时间内行驶的路程s是km。
【总结升华】 用分割、近似代替、求和、取极限这四个步骤可以求曲边多边形的面积,它体现了一种化整(分割)为零,积零为整(逼近)的思想方法。
举一反三:
【变式】 已知某运动物体做变速直线运动,它的速度v是时间t的函数v(t),写出物体在t=0到t=t0这段时间内所经过的路程s的求法。
【答案】
(1)分割
将时间区间[0,t0]分成n等份:
(i=1,2,…,n),
每个小区间所表示的时间为,
各小区间物体运动的路程记作Δsi(i=1,2,…,n)。
(2)近似代替
在每个小区间上以匀速直线运动的路程近似代替变速直线运动的路程:
在小区间上任取一时刻(i=1,2,…,n)。用时刻的速度近似代替第i个小区间上的速度。由匀速直线运动的路程公式,每个小区间物体运动所经过的路程可以近似地表示为
(i=1,2,…,n)。
(3)求和
因为每个小区间上物体运动的路程可以用这一区间上做匀速直线运动的路程近似代替,所以在时间[0,t0]范围物体运动的路程s,就可以用这一物体分别在n个小区间上做n个匀速直线运动的路程和近似代替。
即。 ①
(4)取极限
当所分时间区间愈短,即愈小时,和式①的值就愈接近s。因此,当n趋向于+∞,即趋向于0时,和式①无限趋近于s,所以s就是所求的物体在时间区间[0,t0]上所经过的路程。
类型三、定积分的几何意义
例3. 用定积分的几何意义求:
(1);
(2);
(3)。
【思路点拨】画出简图,结合图形确定积分区间。
【解析】(1)如下图:
阴影部分面积为,
从而。
(2)如右上图:
由于A的面积等于B的面积,
从而。
(3)设,则,表示半径为2的个圆,
由定积分的概念可知,表示如图所示的以2为半径的圆的面积,
所以
【总结升华】
(1)利用定积分的几何意义正确画出图形求定积分。
(2)表示曲边梯形的面积,而上半圆可看做特殊曲边梯形(有两边缩为点),这里面积易求,从而得出定积分的值。
举一反三:
【变式1】(2018 怀化二模)定积分的值为( )
A. B. C.π D.2π
【答案】∵,
∴(x-1)2+y2=1表示以(1,0)为圆心,以1为半径的圆,
∴定积分所围成的面积就是该圆的面积的四分之一,
∴定积分,
故选:A。
【变式2】利用定积分的几何定义求定积分:
(1); (2)
【答案】
(1)设,则表示个圆,
由定积分的概念可知,所求积分就是圆的面积,
所以
(2)设,则表示如图的曲边形,
其面积,
故.
【变式3】
已知甲、乙两车由同一起点同时出发,并沿同一路线(假定为直线)
行驶.甲车、乙车的速度曲线分别为和(如图所示).那么对
于图中给定的和,下列判断中一定正确的是( )
A. 在时刻,甲车在乙车前面
B. 时刻后,甲车在乙车后面
C. 在时刻,两车的位置相同
D. 时刻后,乙车在甲车前面
【答案】A
在时刻,显然甲的曲边图形的面积大于乙,所以甲车在前面,排除C、D; 在时刻,甲的曲边图形的面积明显大于乙,故选A.
类型四、定积分定义和性质的灵活运用
例4. 将和式表示为定积分。
【解析】 ∵
。
【总结升华】 将和式转化为积分形式的关键在于构造出定积分的定义结构,
即。
举一反三:
【变式】试将和式表示成定积分。
【答案】∵
。
例5.利用定积分的性质,用定积分表示曲线y=x―2,x=y2所围成的平面区域的面积。
【解析】如图所示,曲线所围成的平面区域的面积S=SA1+SA2,
A1:由,,x=1围成;
A2:由,y=x―2,x=1和x=4围成;
∴;。
∴。
【总结升华】 利用定积分求平面图形面积时,可按以下步骤进行:
①画图;②确定积分变量;③求交点,确定积分上、下限;④求定积分,得面积。
举一反三:
【变式1】
直线x=0,y=0,x=2与曲线所围所的图形的面积用定积分表示为________。
【答案】。
【变式2】 (2018 会宁县校级模拟)曲线与直线y=x―1及x=4所围成的封闭图形的面积用定积分表示为
【答案】令x=4,代入直线y=x-1得A(4,3),同理得
由,解得x=2,所以曲线与直线y=x-1交于点B(2,1)
∴SABC=S梯形ABEF-SBCEF
而
∵
∴封闭图形ABC的面积SABC=S梯形ABEF-SBCEF=4-。
【巩固练习】
一、选择题
1.等于( )
A.0 B.1 C. D.2
2.设连续函数,则当a<b时,定积分的符号( )
A.一定是正的
B.一定是负的
C.当0<a<b时是正的,当a<b<0时是负的
D.以上结论都不对
3.在求由x=a,x=b(a<b),及y=0围成的曲边梯形的面积S时,在区间[a,b]上等间隔地插入n―1个分点,分别过这些分点作x轴的垂线,把曲边梯形分成n个小曲边梯形,下列说法中正确的个数是( )
①n个小曲边梯形的面积和等于S;
②n个小曲边梯形的面积和小于S;
③n个小曲边梯形的面积和大于S;
④n个小曲边梯形的面积和与S之间的大小关系无法确定。
A.1 B.2 C.3 D.4
4.下列结论中错误的是( )
A.
B.
C.=+(其中
D.=
5.已知为偶函数且,则( )
A.0 B.4 C.8 D.16
6.(2018 陕西模拟)计算的结果是( )
A. B. C. D.
7.(2018春 唐山校级模拟)将和式的极限(P>0)表示成定积分为( )
A. B. C. D.
二、填空题
8.(2018 历下区校级四模改编)由曲线,直线y=x-2及y轴所围成的图形的面积用定积分表示为________。
9.若,则________。
10.若,,则________。
11.若,则由x=0,x=π,及x轴围成的图形的面积为________。
12.________。
三、解答题
13.计算定积分的值。
14.比较与的大小。
15.物体在力F的作用下从静止开始运动,力F的大小位移s(m)的关系是:,求物体运动5 m的过程中力F所做的功。
【答案与解析】
1.【答案】B
【解析】 ∵,故选B。
2.【答案】A
【解析】 由定积分的性质(4)可得,故选A。
3.【答案】A
【解析】 根据“化整为零”“积零为整”的思想知①是正确的,故选A。
4. 【答案】D.
【解析】依据定积分的性质可判断A、B、C是正确的,故选D。
5. 【答案】 D
【解析】为偶函数,则
6.【答案】C
【解析】
表示的几何意义是以(0,0)为圆心,2为半径第一象限内圆弧与坐标轴围成的
面积=,故选:C。
7.【答案】B
【解析】 ∵。
8.【答案】
【解析】如图所示:
联立 解得,∴M(4,2)。
由曲线,直线y=x-2及y轴所围成的图形的面积
。
9.【答案】6
【解析】 由定积分的定义可得。
10.【答案】5
【解析】 ∵。
11.【答案】2
【解析】 由正弦函数与余弦函数的图象,知,x∈[0,π]的图象与x轴围成的图形的面积等于,的图象与x轴围成的图形的面积的2倍,所以。
12.【答案】3
【解析】 ∵。
13.【解析】(―≤x≤0)的图象如右图所示:
所以。
14.【解析】∵,0≤sin x≤1,
∴sin5x≤sin x。
∴。
15.【解析】s∈[0,5],将[0,5]n等分,得,,
则,
在[si―1,si]的位移内,力Fi所做的功
,
所以
。
