人教版高中数学理科选修2-2同步练习题、期中、期末复习资料、补习资料:12微积分基本定理
文档属性
| 名称 | 人教版高中数学理科选修2-2同步练习题、期中、期末复习资料、补习资料:12微积分基本定理 | 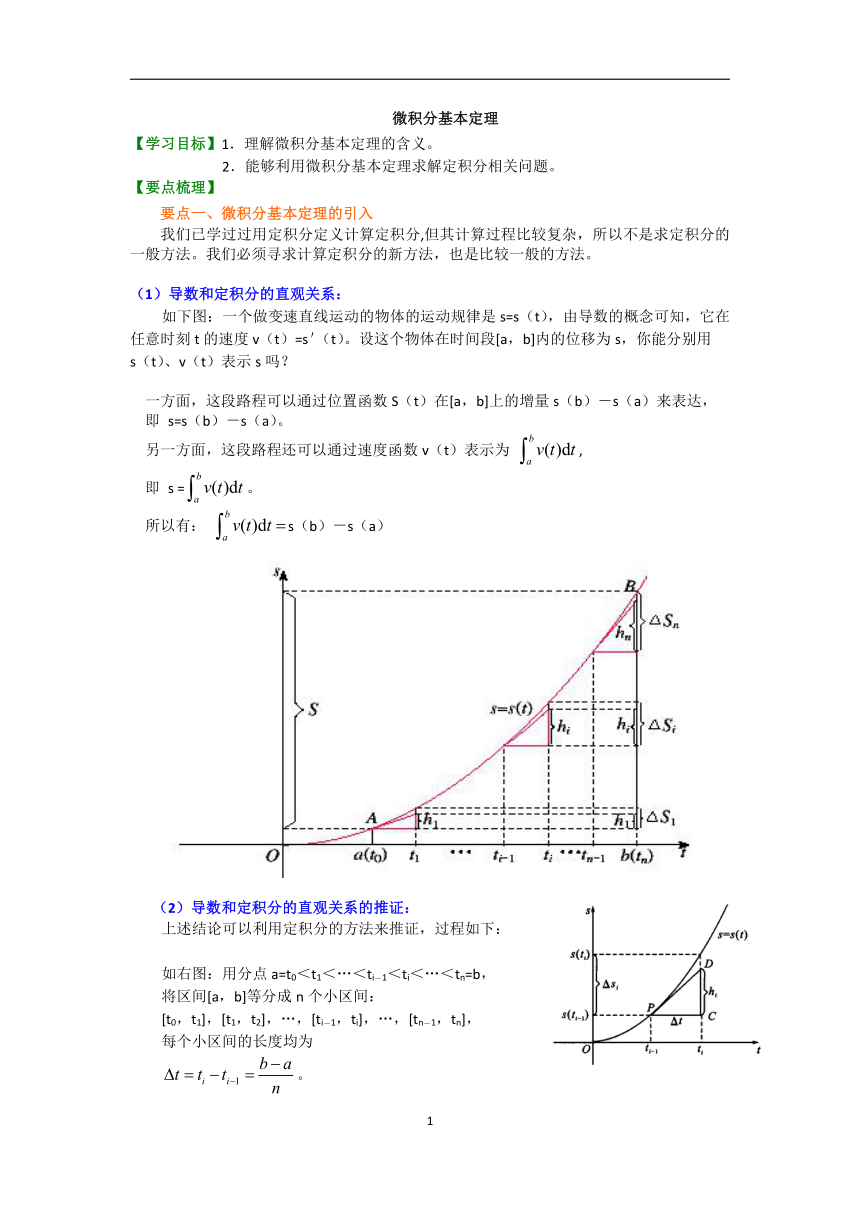 | |
| 格式 | zip | ||
| 文件大小 | 381.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-21 09:45:45 | ||
图片预览





文档简介
微积分基本定理
【学习目标】1.理解微积分基本定理的含义。
2.能够利用微积分基本定理求解定积分相关问题。
【要点梳理】
要点一、微积分基本定理的引入
我们已学过过用定积分定义计算定积分,但其计算过程比较复杂,所以不是求定积分的一般方法。我们必须寻求计算定积分的新方法,也是比较一般的方法。
(1)导数和定积分的直观关系:
如下图:一个做变速直线运动的物体的运动规律是s=s(t),由导数的概念可知,它在任意时刻t的速度v(t)=s'(t)。设这个物体在时间段[a,b]内的位移为s,你能分别用
s(t)、v(t)表示s吗?
一方面,这段路程可以通过位置函数S(t)在[a,b]上的增量s(b)-s(a)来表达,
即 s=s(b)-s(a)。
另一方面,这段路程还可以通过速度函数v(t)表示为 ,
即 s =。
所以有: s(b)-s(a)
(2)导数和定积分的直观关系的推证:
上述结论可以利用定积分的方法来推证,过程如下:
如右图:用分点a=t0<t1<…<ti-1<ti<…<tn=b,
将区间[a,b]等分成n个小区间:
[t0,t1],[t1,t2],…,[ti―1,ti],…,[tn―1,tn],
每个小区间的长度均为
。
当Δt很小时,在[ti―1,ti]上,v(t)的变化很小,可以认为物体近似地以速度v(ti―1)做匀速运动,物体所做的位移
。 ②
从几何意义上看,设曲线s=s(t)上与ti―1对应的点为P,PD是P点处的切线,由导数的几何意义知,切线PD的斜率等于s'(ti―1),于是
。
结合图,可得物体总位移
。
显然,n越大,即Δt越小,区间[a,b]的分划就越细,与s的近似程度就越好。由定积分的定义有
。
结合①有
。
上式表明,如果做变速直线运动的物体的运动规律是s=s(t),那么v(t)=s'(t)在区间[a,b]上的定积分就是物体的位移s(b)―s(a)。
一般地,如果是区间[a,b]上的连续函数,并且,那么。
这个结论叫做微积分基本定理。
要点二、微积分基本定理的概念
微积分基本定理:
一般地,如果,且在[a,b]上可积,则。这个结论叫做微积分基本定理,又叫做牛顿-莱布尼兹公式。
其中,叫做的一个原函数。为了方便,我们常把记作,即。
要点诠释:(1)根据定积分定义求定积分,往往比较困难,而利用上述定理求定积分比较方便。
(2)设是定义在区间I上的一个函数,如果存在函数,在区间I上的任何一点x处都有,那么叫做函数在区间I上的一个原函数。根据定义,求函数的原函数,就是要求一个函数,使它的导数等于。由于,所以也是的原函数,其中c为常数。
(3)利用微积分基本定理求定积分的关键是找出使的函数。通常,我们可以运用基本初等函数的求导公式和导数的四则运算法则从反方向求出。
要点三、定积分的计算
1. 求定积分的一般步骤是:
(1)把被积函数变形为幂函数、正弦函数、余弦函数、指数函数与常数的积的和或差;
(2)把定积分用定积分性质变形为求被积函数为上述函数的定积分;
(3)分别用求导公式找到一个相应的原函数;
(4)利用牛顿―――莱布尼兹公式求出各个定积分的值;
(5)计算原始定积分的值。
2. 定积分的运算性质。
①有限个函数代数和(或差)的定积分等于各个函数定积分的代数和(或差),即
。
②常数因子可提到积分符号前面,即。
③当积分上限与下限交换时,积分值一定要反号,即。
④定积分的可加性,对任意的c,有。
3. 定积分的计算技巧:
(1)对被积函数,要先化简,再求积分。
(2)求被积函数是分段函数的定积分,依据定积分“对区间的可加性”,分段积分再求和。
(3)对于含有绝对值符号的被积函数,要去掉绝对值符号才能积分。
要点诠释:
① 求定积分主要是要找到被积函数的原函数,也就是说,要找到一个函数,它的导函数等于被积函数.因此,求导运算与求原函数运算互为逆运算.
② 把积分上、下限代入原函数求差时,要按步骤进行,以免发生符号错误。
③ 由于也是的原函数,其中c为常数.
【典型例题】
类型一:利用微积分基本定理求定积分
例1.计算下列定积分
(1) (2)
【思路点拨】 根据求导函数与求原函数互为逆运算,找到被积函数的一个原函数,利用微积分基本定理求解.
【解析】(1)因为,所以。
(2)
【总结升华】为使解题步骤清晰,通常都是把求原函数和计算原函数值的差用一串等式表示出来。解题格式如下:有
举一反三:
【变式】计算下列定积分
(1) (2)
(3) (4)
【答案】(1)
(2)
(3)
(4)
例2. 求下列定积分:
(1);(2);
(3);(4)。
【解析】 (1)。
(2)。
(3)。
(4)。
【总结升华】
求函数在某个区间上的定积分,关键是求出函数的一个原函数,
要正确运用求导运算与求原函数运算互为逆运算的关系。
求复杂函数定积分要依据定积分的性质。
举一反三:
【变式1】计算下列定积分的值:
(1), (2)(2018春 银川校级期中), (3)
【答案】
(1)
(2)
(3)
【变式2】计算(1)
(2)
【答案】(1)
(2)
【变式3】计算下列定积分
(1); (2) (3)
【答案】 (1)且,
(2),又,得
所以
(3)由,得
所以
类型二:几类特殊被积函数求定积分问题
例3. 求下列定积分。
(1)(2018 梧州三模)已知函数,求
(2)。
【答案】(1)(2)
【思路点拨】对于图形由两部分组成的函数在求积分时,应注意用性质=+进行化简.
【解析】
(1)∵函数,
∴,
∵表示以原点为圆心,以为半径的圆的面积的四分之一,
∴,
∴
(2)
。
【总结升华】
(1)对于分段函数的定积分,通常是依据定积分“对区间的可加性”,先分段积分再求和,要注意各段定积分的上、下限。
(2)计算时,需要去掉绝对值符号,这时要讨论的正负,转化为分段函数求定积分问题。
举一反三:
【变式1】求定积分:(1), 其中
(2);
【答案】(1)
(2)=+
= +
=
=;
【变式2】计算下列定积分
(1);(2)
【答案】
(1),
(2)∵0≤x≤2,于是
∴
类型三:函数性质在定积分计算中的应用
例4.求定积分:;
【思路点拨】考虑利用被积式函数的奇偶性求积分。
【解析】∵是奇函数,∴,
∵是偶函数,∴
∴
【总结升华】函数的奇偶性又是解决定积分有关问题的重要工具,利用这两点能简捷地解决定积分的有关问题,结论如下:
(1)若是偶函数,则;
(2)若是奇函数,则.
举一反三:
【变式1】求的值
【答案】设, ∵是奇函数,∴。
【变式2】设是偶函数,若,则 ;
【答案】∵是偶函数,∴
【变式3】求定积分:
【答案】
∵是偶函数,
∴.
【巩固练习】
一、选择题
1.(2018春 保定校级期末)下列积分值等于1的是( )
A. B. C. D.
2.定积分区间与被积函数确定以后,则定积分的值一定是( )
A.唯一的 B.不唯一的 C.多于一个的 D.无穷多个的
3.( )
A.sin x B.―cos x C.cos b―sin a D.0
4.已知为偶函数且,则( )
A.0 B.4 C.8 D.16
5.设,则的值是( )
A. B. C. D.
6.=( )
A. B. C. D.
7.定积分( )
A. B. C. D.
二、填空题
8.(2018 大庆二模)________;
9.(2018 齐齐哈尔二模)若,则a的值是________;
10.= ;
11.设函数。若,,则x0的值为________。
三、解答题
12.(12分)设,求。
13.已知,求的最大值。
14.已知是一次函数,其图象过点(1,4),且,求的解析式。
15.一物体在变力作用下沿坐标平面内轴正方向由m处运动到m处,求力做的功.
【答案与解析】
1.【答案】D
【解析】,,表式以原点为圆心以2为半径的圆的面积的一半,故,。
2.【答案】A
【解析】 因为定积分是一个确定的常数。
3.【答案】D
【解析】 ∵为实常数,所以。
4. 【答案】D
【解析】为偶函数,则
5.【答案】D
【解析】 分段函数的定积分问题,必须分段求。
6.【答案】B
【解析】 ∵。
7. 【答案】D
【解析】中的被积函数恰是一个位于x轴上方的半圆,其面积为,故,又
∴
8. 【答案】
【解析】,故答案为:e。
9.【答案】2
【解析】 ,a>1,
∴a2+lna=4+ln2=22+ln2,解得a=2,故答案为:2。
10.【答案】
【解析】原式=
11.【答案】
【解析】 ,∴。
∵a≠0,∴。又0≤x0≤1,∴。
12.【解析】,
设,则,
∴。
设,则,
∴,
∴,
∴。
13.【解析】∵,
∴。
∴当时,的最大值为。
14.【解析】设,因为函数的图象过点(1,4),所以k+b=4。 ①
又,所以。 ②
由①②得k=6,b=―2,所以19.
15.【解析】由题意知力做的功为:
【学习目标】1.理解微积分基本定理的含义。
2.能够利用微积分基本定理求解定积分相关问题。
【要点梳理】
要点一、微积分基本定理的引入
我们已学过过用定积分定义计算定积分,但其计算过程比较复杂,所以不是求定积分的一般方法。我们必须寻求计算定积分的新方法,也是比较一般的方法。
(1)导数和定积分的直观关系:
如下图:一个做变速直线运动的物体的运动规律是s=s(t),由导数的概念可知,它在任意时刻t的速度v(t)=s'(t)。设这个物体在时间段[a,b]内的位移为s,你能分别用
s(t)、v(t)表示s吗?
一方面,这段路程可以通过位置函数S(t)在[a,b]上的增量s(b)-s(a)来表达,
即 s=s(b)-s(a)。
另一方面,这段路程还可以通过速度函数v(t)表示为 ,
即 s =。
所以有: s(b)-s(a)
(2)导数和定积分的直观关系的推证:
上述结论可以利用定积分的方法来推证,过程如下:
如右图:用分点a=t0<t1<…<ti-1<ti<…<tn=b,
将区间[a,b]等分成n个小区间:
[t0,t1],[t1,t2],…,[ti―1,ti],…,[tn―1,tn],
每个小区间的长度均为
。
当Δt很小时,在[ti―1,ti]上,v(t)的变化很小,可以认为物体近似地以速度v(ti―1)做匀速运动,物体所做的位移
。 ②
从几何意义上看,设曲线s=s(t)上与ti―1对应的点为P,PD是P点处的切线,由导数的几何意义知,切线PD的斜率等于s'(ti―1),于是
。
结合图,可得物体总位移
。
显然,n越大,即Δt越小,区间[a,b]的分划就越细,与s的近似程度就越好。由定积分的定义有
。
结合①有
。
上式表明,如果做变速直线运动的物体的运动规律是s=s(t),那么v(t)=s'(t)在区间[a,b]上的定积分就是物体的位移s(b)―s(a)。
一般地,如果是区间[a,b]上的连续函数,并且,那么。
这个结论叫做微积分基本定理。
要点二、微积分基本定理的概念
微积分基本定理:
一般地,如果,且在[a,b]上可积,则。这个结论叫做微积分基本定理,又叫做牛顿-莱布尼兹公式。
其中,叫做的一个原函数。为了方便,我们常把记作,即。
要点诠释:(1)根据定积分定义求定积分,往往比较困难,而利用上述定理求定积分比较方便。
(2)设是定义在区间I上的一个函数,如果存在函数,在区间I上的任何一点x处都有,那么叫做函数在区间I上的一个原函数。根据定义,求函数的原函数,就是要求一个函数,使它的导数等于。由于,所以也是的原函数,其中c为常数。
(3)利用微积分基本定理求定积分的关键是找出使的函数。通常,我们可以运用基本初等函数的求导公式和导数的四则运算法则从反方向求出。
要点三、定积分的计算
1. 求定积分的一般步骤是:
(1)把被积函数变形为幂函数、正弦函数、余弦函数、指数函数与常数的积的和或差;
(2)把定积分用定积分性质变形为求被积函数为上述函数的定积分;
(3)分别用求导公式找到一个相应的原函数;
(4)利用牛顿―――莱布尼兹公式求出各个定积分的值;
(5)计算原始定积分的值。
2. 定积分的运算性质。
①有限个函数代数和(或差)的定积分等于各个函数定积分的代数和(或差),即
。
②常数因子可提到积分符号前面,即。
③当积分上限与下限交换时,积分值一定要反号,即。
④定积分的可加性,对任意的c,有。
3. 定积分的计算技巧:
(1)对被积函数,要先化简,再求积分。
(2)求被积函数是分段函数的定积分,依据定积分“对区间的可加性”,分段积分再求和。
(3)对于含有绝对值符号的被积函数,要去掉绝对值符号才能积分。
要点诠释:
① 求定积分主要是要找到被积函数的原函数,也就是说,要找到一个函数,它的导函数等于被积函数.因此,求导运算与求原函数运算互为逆运算.
② 把积分上、下限代入原函数求差时,要按步骤进行,以免发生符号错误。
③ 由于也是的原函数,其中c为常数.
【典型例题】
类型一:利用微积分基本定理求定积分
例1.计算下列定积分
(1) (2)
【思路点拨】 根据求导函数与求原函数互为逆运算,找到被积函数的一个原函数,利用微积分基本定理求解.
【解析】(1)因为,所以。
(2)
【总结升华】为使解题步骤清晰,通常都是把求原函数和计算原函数值的差用一串等式表示出来。解题格式如下:有
举一反三:
【变式】计算下列定积分
(1) (2)
(3) (4)
【答案】(1)
(2)
(3)
(4)
例2. 求下列定积分:
(1);(2);
(3);(4)。
【解析】 (1)。
(2)。
(3)。
(4)。
【总结升华】
求函数在某个区间上的定积分,关键是求出函数的一个原函数,
要正确运用求导运算与求原函数运算互为逆运算的关系。
求复杂函数定积分要依据定积分的性质。
举一反三:
【变式1】计算下列定积分的值:
(1), (2)(2018春 银川校级期中), (3)
【答案】
(1)
(2)
(3)
【变式2】计算(1)
(2)
【答案】(1)
(2)
【变式3】计算下列定积分
(1); (2) (3)
【答案】 (1)且,
(2),又,得
所以
(3)由,得
所以
类型二:几类特殊被积函数求定积分问题
例3. 求下列定积分。
(1)(2018 梧州三模)已知函数,求
(2)。
【答案】(1)(2)
【思路点拨】对于图形由两部分组成的函数在求积分时,应注意用性质=+进行化简.
【解析】
(1)∵函数,
∴,
∵表示以原点为圆心,以为半径的圆的面积的四分之一,
∴,
∴
(2)
。
【总结升华】
(1)对于分段函数的定积分,通常是依据定积分“对区间的可加性”,先分段积分再求和,要注意各段定积分的上、下限。
(2)计算时,需要去掉绝对值符号,这时要讨论的正负,转化为分段函数求定积分问题。
举一反三:
【变式1】求定积分:(1), 其中
(2);
【答案】(1)
(2)=+
= +
=
=;
【变式2】计算下列定积分
(1);(2)
【答案】
(1),
(2)∵0≤x≤2,于是
∴
类型三:函数性质在定积分计算中的应用
例4.求定积分:;
【思路点拨】考虑利用被积式函数的奇偶性求积分。
【解析】∵是奇函数,∴,
∵是偶函数,∴
∴
【总结升华】函数的奇偶性又是解决定积分有关问题的重要工具,利用这两点能简捷地解决定积分的有关问题,结论如下:
(1)若是偶函数,则;
(2)若是奇函数,则.
举一反三:
【变式1】求的值
【答案】设, ∵是奇函数,∴。
【变式2】设是偶函数,若,则 ;
【答案】∵是偶函数,∴
【变式3】求定积分:
【答案】
∵是偶函数,
∴.
【巩固练习】
一、选择题
1.(2018春 保定校级期末)下列积分值等于1的是( )
A. B. C. D.
2.定积分区间与被积函数确定以后,则定积分的值一定是( )
A.唯一的 B.不唯一的 C.多于一个的 D.无穷多个的
3.( )
A.sin x B.―cos x C.cos b―sin a D.0
4.已知为偶函数且,则( )
A.0 B.4 C.8 D.16
5.设,则的值是( )
A. B. C. D.
6.=( )
A. B. C. D.
7.定积分( )
A. B. C. D.
二、填空题
8.(2018 大庆二模)________;
9.(2018 齐齐哈尔二模)若,则a的值是________;
10.= ;
11.设函数。若,,则x0的值为________。
三、解答题
12.(12分)设,求。
13.已知,求的最大值。
14.已知是一次函数,其图象过点(1,4),且,求的解析式。
15.一物体在变力作用下沿坐标平面内轴正方向由m处运动到m处,求力做的功.
【答案与解析】
1.【答案】D
【解析】,,表式以原点为圆心以2为半径的圆的面积的一半,故,。
2.【答案】A
【解析】 因为定积分是一个确定的常数。
3.【答案】D
【解析】 ∵为实常数,所以。
4. 【答案】D
【解析】为偶函数,则
5.【答案】D
【解析】 分段函数的定积分问题,必须分段求。
6.【答案】B
【解析】 ∵。
7. 【答案】D
【解析】中的被积函数恰是一个位于x轴上方的半圆,其面积为,故,又
∴
8. 【答案】
【解析】,故答案为:e。
9.【答案】2
【解析】 ,a>1,
∴a2+lna=4+ln2=22+ln2,解得a=2,故答案为:2。
10.【答案】
【解析】原式=
11.【答案】
【解析】 ,∴。
∵a≠0,∴。又0≤x0≤1,∴。
12.【解析】,
设,则,
∴。
设,则,
∴,
∴,
∴。
13.【解析】∵,
∴。
∴当时,的最大值为。
14.【解析】设,因为函数的图象过点(1,4),所以k+b=4。 ①
又,所以。 ②
由①②得k=6,b=―2,所以19.
15.【解析】由题意知力做的功为:
