人教新课标B版 必修1 第三章 基本初等函数(Ⅰ)3.3 幂函数 课件(23张PPT)
文档属性
| 名称 | 人教新课标B版 必修1 第三章 基本初等函数(Ⅰ)3.3 幂函数 课件(23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-21 00:00:00 | ||
图片预览








文档简介
课件23张PPT。书山有路 学海无涯第三章
基本初函数3.3 幂函数问题引入 (1)如果回收旧报纸每公斤1元,某班每年卖旧报纸x公斤,所得价钱y是关于x的函数; (2) 如果正方形的边长为x,面积y,这里y是关于x的函数;
(3) 如果正方体的边长为x, 正方体的体积为y, 这里y是关于x函数;
(4)如果一个正方形场地的面积为x, 这个正方形的边长为y,这里y是关于x的函数;
(5)如果某人x秒内骑车行驶了1km,他骑车的平均速度是y,这里y是关于x的函数.
我们先看几个具体问题: 1:以上各题目中所体现的函数关系分别是什么?
2:以上问题中的函数解析式具有什么共同特征?定义说明:(1)底数是自变量x;
(2)指数是常数a;
(3)函数式前的系数是1;
(4)只有一项。 结构特征幂函数与指数函数的对比底数指数指数底数幂值幂值◆判断一个函数是幂函数还是指数函数切入点看自变量x是指数还是底数幂函数指数函数判断下列函数是否为幂函数。(1) y=x4 (3) y= -x2 (2) y=2x2 (6) y=x3+2 牛刀小试 练习1牛刀小试 练习2已知幂函数过点(3,27),求函数f(x)。待定系数法
画出以下幂函数图象的草图,并填好相应的函数性质表格。 学生活动要求:
1.小组同学合作
2.用描点法
3.在一个直角坐标系内
4.用五种颜色的彩笔
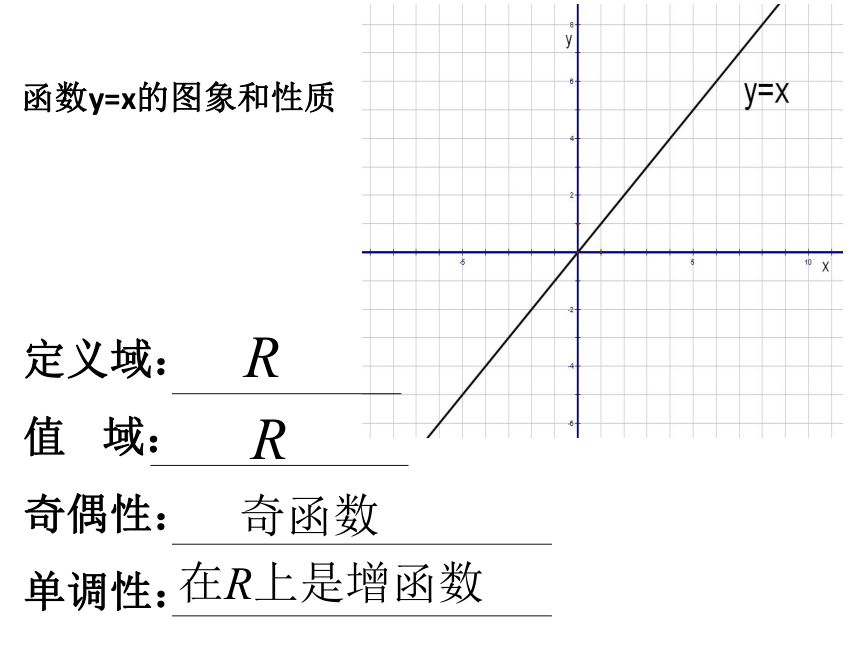
函数y=x的图象和性质函数y=x2的图象和性质函数y=x3的图象和性质函数y=x-1的图象 和性质在( -∞,0)和(0, +∞ )上是减函数合作探究:观察幂函数图象,将发现的结论填在下面表格内:RRR[0,+∞)R[0,+∞)R[0,+∞)奇函数偶函数奇函数非奇非偶函数奇函数R上是增函数在(-∞,0]上是减函数,
在(0, +∞)上是增函数R上是增函数在(0,+∞)上是增函数在( -∞,0)和(0, +∞ )上是减函数奇偶性一、三一、二一、三一一、三幂函数的性质:1.所有的幂函数在(0,+∞)都有定义,并且函数图象都通过点(1,1);
幂函数的定义域、奇偶性、单调性,因函数式中a的不同而各异.3.如果a<0,则幂函数的图象过点(1,1),
并在(0,+∞)上为减函数;
2.如果a>0,则幂函数的图象
过点(0,0),(1,1)
并在(0,+∞)上为增函数;
4.所有的幂函数在(1,+∞)上,
指大图高。
例1. 利用单调性判断下列各值的大小。(1)5.20.8 与 5.30.8
(2)2.5-0.4 与 2.7-0.4解:(1)y= x0.8 在(0, +∞)内是增函数,
∵5.2<5.3 ∴ 5.20.8 < 5.30.8
(2)y=x-0.4在(0,+∞)内是减函数
∵2.5<2.7∴ 2.5-2/5>2.7-2/5 性质应用
变式:比较下列各数的大小<解后反思
两个幂值比较大小时,何时用幂函数模型,何时用指数函数模型?
0.20.3 , 0.30.3, 0.30.2 解:0.20.3 0.30.3 0.30.2<指数相同的幂的大小比较,利用幂函数的单调性;
底数相同的幂的大小比较,利用指数函数的单调性。 性质应用
构造函数法例2. 试写出函数 的定义域,值域,奇偶性,作出它的图象,并根据函数的图象说明函数的增减性. 它在(0,+∞)上为减函数,
在(-∞,0)上为增函数
性质应用
例3:
如果函数
是幂函数,且在区间(0,+∞)内是减
函数,求满足条件的实数m。
性质应用
性质应用
课堂小结一、幂函数的概念.
二、幂函数图像及性质.(注意第一象限内的 图像)
三、幂函数性质的应用.
1.比较大小
2.求解析式
3.讨论定义域,值域,单调性,奇偶性
4.求参数的取值范围【归纳小结】 教材P110习题3-3A
1、2、3 、4
【课后作业】 同学们,你们今天很棒!加油!Company Logo08:44www.themegallery.com
基本初函数3.3 幂函数问题引入 (1)如果回收旧报纸每公斤1元,某班每年卖旧报纸x公斤,所得价钱y是关于x的函数; (2) 如果正方形的边长为x,面积y,这里y是关于x的函数;
(3) 如果正方体的边长为x, 正方体的体积为y, 这里y是关于x函数;
(4)如果一个正方形场地的面积为x, 这个正方形的边长为y,这里y是关于x的函数;
(5)如果某人x秒内骑车行驶了1km,他骑车的平均速度是y,这里y是关于x的函数.
我们先看几个具体问题: 1:以上各题目中所体现的函数关系分别是什么?
2:以上问题中的函数解析式具有什么共同特征?定义说明:(1)底数是自变量x;
(2)指数是常数a;
(3)函数式前的系数是1;
(4)只有一项。 结构特征幂函数与指数函数的对比底数指数指数底数幂值幂值◆判断一个函数是幂函数还是指数函数切入点看自变量x是指数还是底数幂函数指数函数判断下列函数是否为幂函数。(1) y=x4 (3) y= -x2 (2) y=2x2 (6) y=x3+2 牛刀小试 练习1牛刀小试 练习2已知幂函数过点(3,27),求函数f(x)。待定系数法
画出以下幂函数图象的草图,并填好相应的函数性质表格。 学生活动要求:
1.小组同学合作
2.用描点法
3.在一个直角坐标系内
4.用五种颜色的彩笔
函数y=x的图象和性质函数y=x2的图象和性质函数y=x3的图象和性质函数y=x-1的图象 和性质在( -∞,0)和(0, +∞ )上是减函数合作探究:观察幂函数图象,将发现的结论填在下面表格内:RRR[0,+∞)R[0,+∞)R[0,+∞)奇函数偶函数奇函数非奇非偶函数奇函数R上是增函数在(-∞,0]上是减函数,
在(0, +∞)上是增函数R上是增函数在(0,+∞)上是增函数在( -∞,0)和(0, +∞ )上是减函数奇偶性一、三一、二一、三一一、三幂函数的性质:1.所有的幂函数在(0,+∞)都有定义,并且函数图象都通过点(1,1);
幂函数的定义域、奇偶性、单调性,因函数式中a的不同而各异.3.如果a<0,则幂函数的图象过点(1,1),
并在(0,+∞)上为减函数;
2.如果a>0,则幂函数的图象
过点(0,0),(1,1)
并在(0,+∞)上为增函数;
4.所有的幂函数在(1,+∞)上,
指大图高。
例1. 利用单调性判断下列各值的大小。(1)5.20.8 与 5.30.8
(2)2.5-0.4 与 2.7-0.4解:(1)y= x0.8 在(0, +∞)内是增函数,
∵5.2<5.3 ∴ 5.20.8 < 5.30.8
(2)y=x-0.4在(0,+∞)内是减函数
∵2.5<2.7∴ 2.5-2/5>2.7-2/5 性质应用
变式:比较下列各数的大小<解后反思
两个幂值比较大小时,何时用幂函数模型,何时用指数函数模型?
0.20.3 , 0.30.3, 0.30.2 解:0.20.3 0.30.3 0.30.2<指数相同的幂的大小比较,利用幂函数的单调性;
底数相同的幂的大小比较,利用指数函数的单调性。 性质应用
构造函数法例2. 试写出函数 的定义域,值域,奇偶性,作出它的图象,并根据函数的图象说明函数的增减性. 它在(0,+∞)上为减函数,
在(-∞,0)上为增函数
性质应用
例3:
如果函数
是幂函数,且在区间(0,+∞)内是减
函数,求满足条件的实数m。
性质应用
性质应用
课堂小结一、幂函数的概念.
二、幂函数图像及性质.(注意第一象限内的 图像)
三、幂函数性质的应用.
1.比较大小
2.求解析式
3.讨论定义域,值域,单调性,奇偶性
4.求参数的取值范围【归纳小结】 教材P110习题3-3A
1、2、3 、4
【课后作业】 同学们,你们今天很棒!加油!Company Logo08:44www.themegallery.com
