人教新课标B版>必修1>第三章 基本初等函数(Ⅰ)3.1.2 指数函数 课件(20张PPT)
文档属性
| 名称 | 人教新课标B版>必修1>第三章 基本初等函数(Ⅰ)3.1.2 指数函数 课件(20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 280.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-21 00:00:00 | ||
图片预览






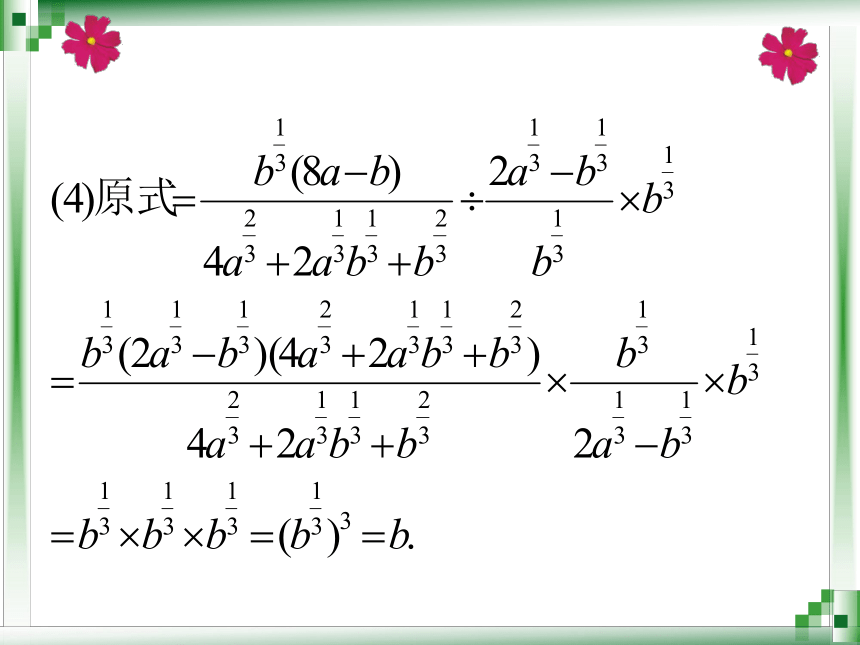


文档简介
课件20张PPT。专题八 指数式与指数函数一、指数式1.整数指数幂的运算性质(1)am·an=am+n (m, n∈Z); (2)am÷an=am-n
(a?0, m, n∈Z); (3)(am)n=amn (m, n∈Z); (4)(ab)n=anbn (n∈Z). 2.根式的概念 如果一个数的 n 次方等于 a(n>1 且 n∈N*), 那么这个数叫做 a 的 n 次方根. 即: 若 xn=a, 则 x 叫做 a 的 n 次方根, 其中 n>1且 n∈N*. 3.根式的性质5.负数没有偶次方根.6.零的任何次方根都是零.一、指数式4.有理数指数幂(1)幂的有关概念
①正整数指数幂:
(n∈N*);
②零指数幂:
a0=____(a≠0);
③负整数指数幂:
a-p=_____(a≠0,p∈N*);1④正分数指数幂: =_______
(a>0,m、n∈N*,且n>1);
⑤负分数指数幂: = =
(a>0,m、n∈N*,且n>1).
⑥0的正分数指数幂等于______,
0的负分数指数幂_____________.
(2)有理数指数幂的性质
①aras= ______(a>0,r、s∈Q);
②(ar)s= ______(a>0,r、s∈Q);
③(ab)r= _______(a>0,b>0,r∈Q). 0没有意义ar+sarsarbr
【例1】计算下列各式:题型一 指数幂的化简与求值
解 二、指数函数 函数 y=ax(a>0, 且a?1)叫做指数函数, 其中 x 是自变量, 函数的定义域是 R.1.指数函数的定义说明:指数函数有以下特点:(1)自变量在指数上,且系数为1;(2)底数是常数,且大于0不等于1;(3)幂式前面的系数为1。画出下列指数函数的函数图像2.指数函数的图象和性质R(0,+∞)(0,1)y>101增函数减函数
根式运算或根式与指数式混合运算时,将
根式化为指数式计算较为方便,对于计算的结果,不
强求统一用什么形式来表示,如果有特殊要求,要根
据要求写出结果.但结果不能同时含有根号和分数指
数,也不能既有分母又含有负指数. 探究提高知能迁移1 解【例3】已知函数
(1)作出图象;
(2)由图象指出其单调区间;
(3)由图象指出当x取什么值时函数有最值.
题型二 指数函数的图象及应用解 (1)由已知可得
其图象由两部分组成:
一部分是:
另一部分是:y=3x (x<0) y=3x+1 (x<-1). 向左平移
1个单位向左平移
1个单位图象如图:
(2)由图象知函数在(-∞,-1]上是增函数,
在(-1,+∞)上是减函数.
(3)由图象知当x=-1时,函数有最大值1,无最小值.
在作函数图象时,首先要研究函数与某一
基本函数的关系.然后通过平移或伸缩来完成. 探究提高知能迁移3 若直线y=2a与函数y=|ax-1| (a>0,且a≠
1)的图象有两个公共点,则a的取值范围是______.
解析 数形结合.
当a>1时,如图①,只有一个公共点,不符合题意.
当01.单调性是指数函数的重要性质,特别是函数图象的
无限伸展性,x轴是函数图象的渐近线.当0 x→+∞时,y→0;当a>1,x→-∞时,y→0;当a>1时,
a的值越大,图象越靠近y轴,递增的速度越快;
当0 度越快.
2.画指数函数y=ax的图象,应抓住三个关键点:(1,a)、
(0,1)、(-1, ). 思想方法 感悟提高方法与技巧3.在有关根式、分数指数幂的变形、求值过程中,要
注意运用方程的观点处理问题,通过解方程(组)
来求值,或用换元法转化为方程来求解.
1.指数函数y=ax (a>0,a≠1)的图象和性质与a的取值
有关,要特别注意区分a>1与02.对可化为a2x+b·ax+c=0或a2x+b·ax+c≥0 (≤0)的
指数方程或不等式,常借助换元法解决,但应注意
换元后“新元”的范围. 失误与防范祝你进步!
(a?0, m, n∈Z); (3)(am)n=amn (m, n∈Z); (4)(ab)n=anbn (n∈Z). 2.根式的概念 如果一个数的 n 次方等于 a(n>1 且 n∈N*), 那么这个数叫做 a 的 n 次方根. 即: 若 xn=a, 则 x 叫做 a 的 n 次方根, 其中 n>1且 n∈N*. 3.根式的性质5.负数没有偶次方根.6.零的任何次方根都是零.一、指数式4.有理数指数幂(1)幂的有关概念
①正整数指数幂:
(n∈N*);
②零指数幂:
a0=____(a≠0);
③负整数指数幂:
a-p=_____(a≠0,p∈N*);1④正分数指数幂: =_______
(a>0,m、n∈N*,且n>1);
⑤负分数指数幂: = =
(a>0,m、n∈N*,且n>1).
⑥0的正分数指数幂等于______,
0的负分数指数幂_____________.
(2)有理数指数幂的性质
①aras= ______(a>0,r、s∈Q);
②(ar)s= ______(a>0,r、s∈Q);
③(ab)r= _______(a>0,b>0,r∈Q). 0没有意义ar+sarsarbr
【例1】计算下列各式:题型一 指数幂的化简与求值
解 二、指数函数 函数 y=ax(a>0, 且a?1)叫做指数函数, 其中 x 是自变量, 函数的定义域是 R.1.指数函数的定义说明:指数函数有以下特点:(1)自变量在指数上,且系数为1;(2)底数是常数,且大于0不等于1;(3)幂式前面的系数为1。画出下列指数函数的函数图像2.指数函数的图象和性质R(0,+∞)(0,1)y>10
根式运算或根式与指数式混合运算时,将
根式化为指数式计算较为方便,对于计算的结果,不
强求统一用什么形式来表示,如果有特殊要求,要根
据要求写出结果.但结果不能同时含有根号和分数指
数,也不能既有分母又含有负指数. 探究提高知能迁移1 解【例3】已知函数
(1)作出图象;
(2)由图象指出其单调区间;
(3)由图象指出当x取什么值时函数有最值.
题型二 指数函数的图象及应用解 (1)由已知可得
其图象由两部分组成:
一部分是:
另一部分是:y=3x (x<0) y=3x+1 (x<-1). 向左平移
1个单位向左平移
1个单位图象如图:
(2)由图象知函数在(-∞,-1]上是增函数,
在(-1,+∞)上是减函数.
(3)由图象知当x=-1时,函数有最大值1,无最小值.
在作函数图象时,首先要研究函数与某一
基本函数的关系.然后通过平移或伸缩来完成. 探究提高知能迁移3 若直线y=2a与函数y=|ax-1| (a>0,且a≠
1)的图象有两个公共点,则a的取值范围是______.
解析 数形结合.
当a>1时,如图①,只有一个公共点,不符合题意.
当0
无限伸展性,x轴是函数图象的渐近线.当0
a的值越大,图象越靠近y轴,递增的速度越快;
当0
2.画指数函数y=ax的图象,应抓住三个关键点:(1,a)、
(0,1)、(-1, ). 思想方法 感悟提高方法与技巧3.在有关根式、分数指数幂的变形、求值过程中,要
注意运用方程的观点处理问题,通过解方程(组)
来求值,或用换元法转化为方程来求解.
1.指数函数y=ax (a>0,a≠1)的图象和性质与a的取值
有关,要特别注意区分a>1与0
指数方程或不等式,常借助换元法解决,但应注意
换元后“新元”的范围. 失误与防范祝你进步!
