人教新课标B版>必修1>第三章 基本初等函数(Ⅰ)3.2.2 对数函数 课件(31张PPT)
文档属性
| 名称 | 人教新课标B版>必修1>第三章 基本初等函数(Ⅰ)3.2.2 对数函数 课件(31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-21 00:00:00 | ||
图片预览







文档简介
课件31张PPT。3.2.2 对数函数
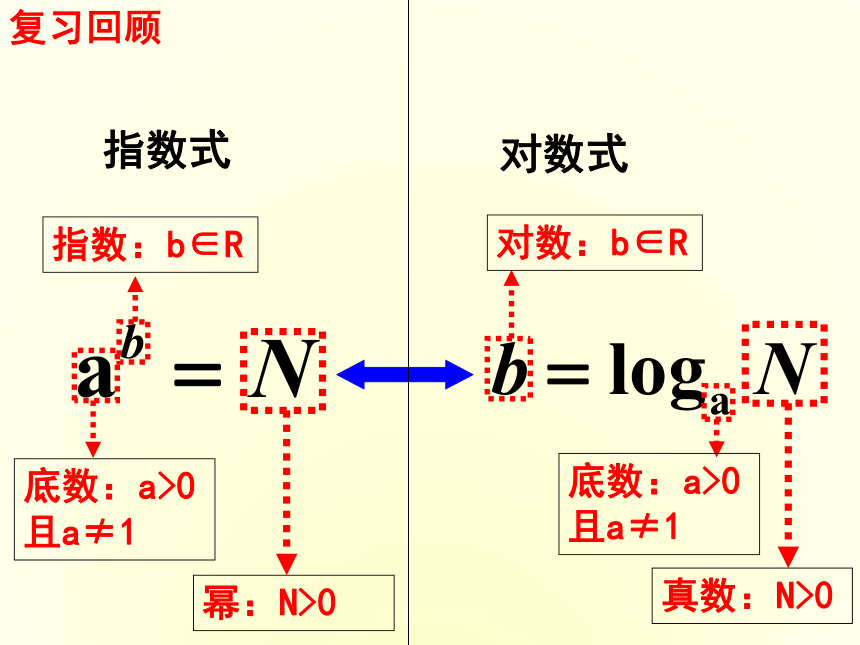
知 识 改 变 命 运,勤 奋 创 造 奇 迹.复习回顾底数:a>0且a≠1幂:N>0真数:N>0底数:a>0且a≠1指数:b∈R对数:b∈R 指数式对数式 由前面的学习我们知道:有一种细胞分裂时,由1个分裂成2个,2个分裂成4个,··· 1个这样的细胞分裂x次会得到多少个细胞?如果知道了细胞的个数y如何确定分裂的次数x呢?由对数式与指数式的互化可知:上式可以看作以y自变量的函数表达式吗?引入新知: 对于每一个给定的y值都有惟一的x的值与之对应,把y看作自变量,x就是y的函数,但习惯上仍用x表示自变量,y表示它的函数:即这就是本节课要学习的:, 对数函数
判断:以下函数是对数函数的是 ( )
A. y=log2(3x-2) B. y=log(x-1)x
C. y=log1/3x2 D.y=lnx
E.y=3log2x+5D (0,+∞)。在同一坐标系中用描点法画出对数函数
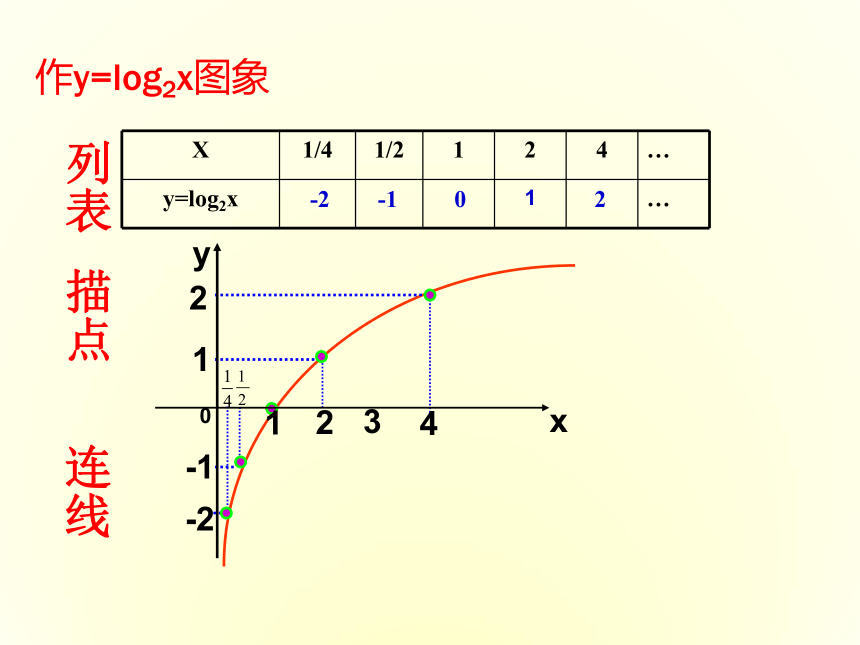
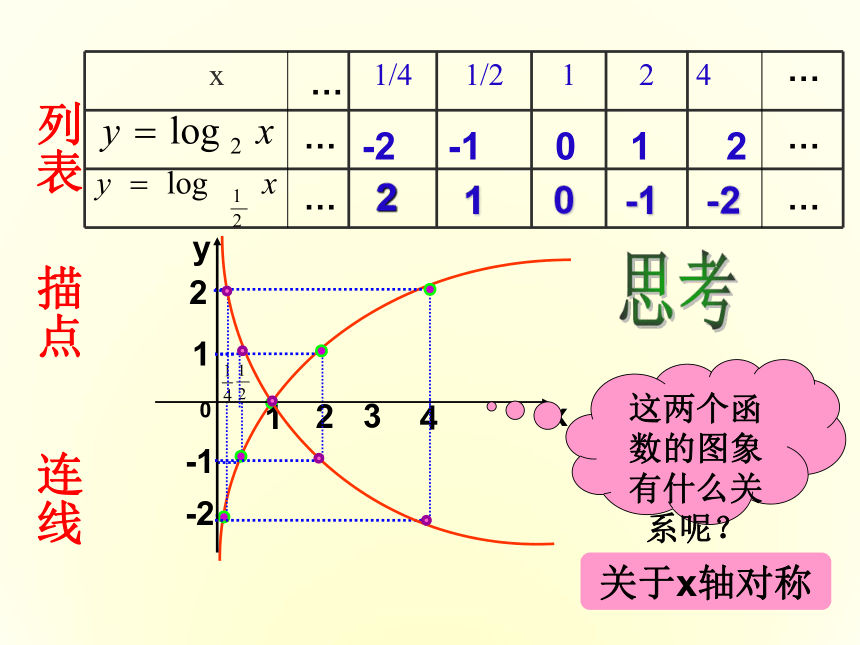
的图象。③用平滑曲线连接。对数函数:y = loga x (a>0,且a≠ 1) 的图象探究:画函数图象的步骤:①列表,②描点,列表描点作y=log2x图象连线-2-1012列表描点连线 -2 -1 0 1 2 思考这两个函数的图象有什么关系呢?关于x轴对称… … … … … … 1 0-1-22定义域 : 值 域 :R
增函数在(0,+∞)上是:
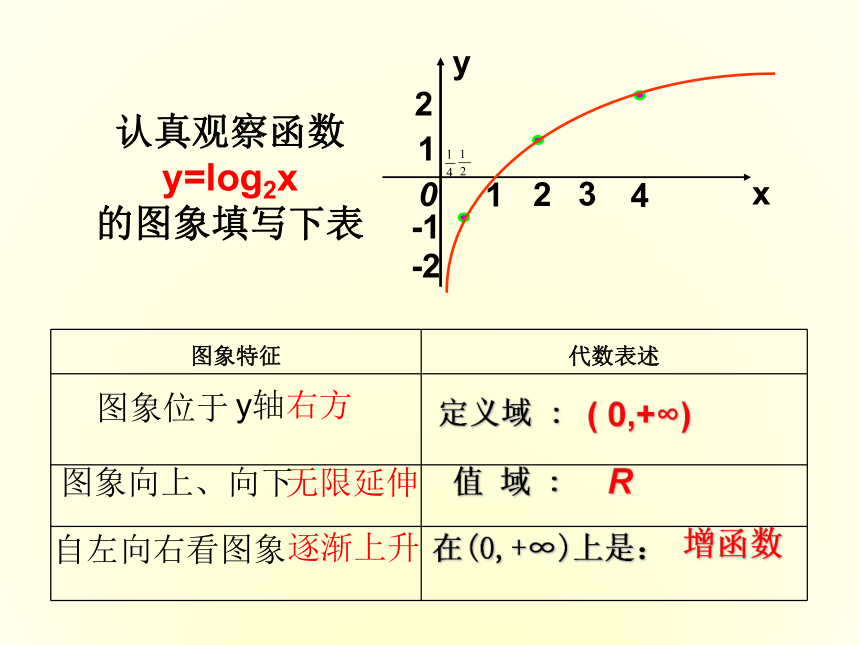
认真观察函数y=log2x
的图象填写下表图象位于图象向上、向下自左向右看图象21-1-21240
y x3y轴右方( 0,+∞)无限延伸逐渐上升定义域 :( 0,+∞) 值 域 :R
减函数在(0,+∞)上是:图象位于图象向上、向下自左向右看图象
认真观察函数
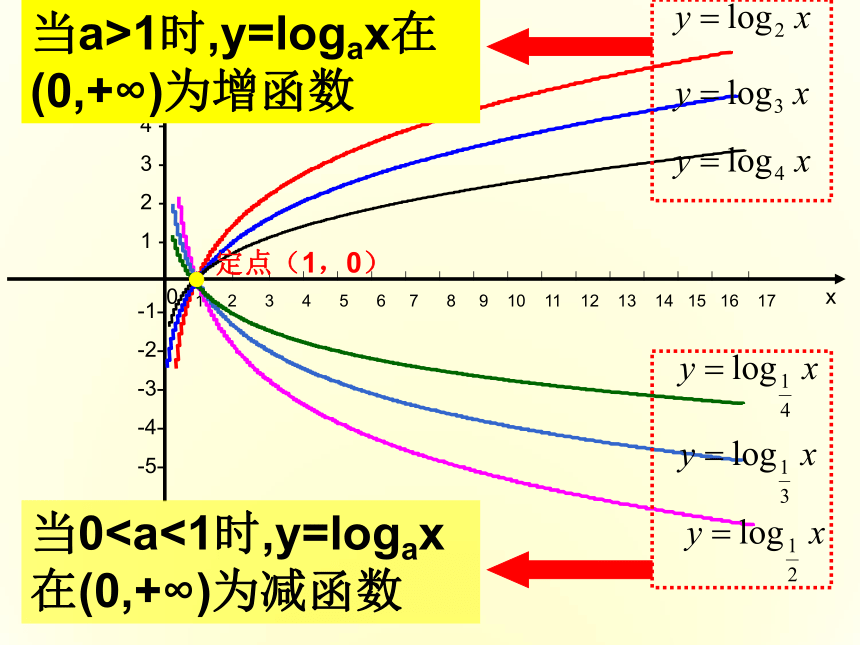
的图象填写下表y轴右方无限延伸逐渐下降思考:从图中你能发现对数函数图像有什么特点?探究:函数 性质当a>1时,y=logax在(0,+∞)为增函数当00当x=1时,总有loga1=0如:log1.059.8
>0比如:log30.9<0即不论底数在a>1或0当x=1时,总有loga1=0比如:log0.39 <0比如:log0.50.8
>0底数和真数的范围相同,则对数大于0;底数和真数的范围不同,则对数小于0;
同正异负 例1.求下列函数的定义域:(1) y=logax2 (2) y=loga(4-x)解:(1)要使函数有意义,必须x2>0,所以x≠?,
即函数y=logax2的定义域为 ?-???? ? (0,+?? (2)要使函数有意义,必须4-x>0,所以x<4,
即函数y=loga(4-x)的定义域为(-??4)应用举例练习二:求下列函数的定义域: 解:3.48.5log 28.5log 23.4且 3.4 < 8.5 因为函数
在(0,+∞)上是增函数,
所以构造函数 例2.比较下列各组数中两个数的大小:当 时方法:①利用对数函数的单调性.
②分类讨论
③用“中间值法”.
构造函数>当 时(4) log56,log65∵构造函数练习三:比较下列各组数中两个数的大小:<<>例3.已知log0.7(3m) ∴3m>m-1>0∴m>11.对数函数的定义:函数
函数的定义域是(0,+∞)。叫做对数函数,其中x是自变量,注:1 、对数函数的定义与指数函数类似,都是形式
定义,注意辨别。2 、对数函数对底数的限制: (a?0,且a ?1)(a?0,且a ?1)一般地,我们把课堂小结:这节课你学到了什么?2.对数函数的图象和性质
(0,+∞)过点(1,0),即当x=1时,y=0 增减1 3.已知函数( -1,3]1.函数 的定义域为 。 2. 比较大小:1) log23 log23.5
2) log0.71.6 log0.71.8< >巩固练习:2.思考:对数函数:y = loga x (a>0,且a≠ 1) 图象随着a取值变化图象如何变化?有规律吗?规律:在x轴
上方图象自左
向右底数越来
越大!x作业: 1.教材P104 A组T2 B组T1Clog,log,log,log则下列式子中正确的是( )的图像如图所示, 3.函数xyxyxyx ydcba=== =再 见
判断:以下函数是对数函数的是 ( )
A. y=log2(3x-2) B. y=log(x-1)x
C. y=log1/3x2 D.y=lnx
E.y=3log2x+5D (0,+∞)。在同一坐标系中用描点法画出对数函数
的图象。③用平滑曲线连接。对数函数:y = loga x (a>0,且a≠ 1) 的图象探究:画函数图象的步骤:①列表,②描点,列表描点作y=log2x图象连线-2-1012列表描点连线 -2 -1 0 1 2 思考这两个函数的图象有什么关系呢?关于x轴对称… … … … … … 1 0-1-22定义域 : 值 域 :R
增函数在(0,+∞)上是:
认真观察函数y=log2x
的图象填写下表图象位于图象向上、向下自左向右看图象21-1-21240
y x3y轴右方( 0,+∞)无限延伸逐渐上升定义域 :( 0,+∞) 值 域 :R
减函数在(0,+∞)上是:图象位于图象向上、向下自左向右看图象
认真观察函数
的图象填写下表y轴右方无限延伸逐渐下降思考:从图中你能发现对数函数图像有什么特点?探究:函数 性质当a>1时,y=logax在(0,+∞)为增函数当0
>0比如:log30.9<0即不论底数在a>1或0
>0底数和真数的范围相同,则对数大于0;底数和真数的范围不同,则对数小于0;
同正异负 例1.求下列函数的定义域:(1) y=logax2 (2) y=loga(4-x)解:(1)要使函数有意义,必须x2>0,所以x≠?,
即函数y=logax2的定义域为 ?-???? ? (0,+?? (2)要使函数有意义,必须4-x>0,所以x<4,
即函数y=loga(4-x)的定义域为(-??4)应用举例练习二:求下列函数的定义域: 解:3.48.5log 28.5log 23.4且 3.4 < 8.5 因为函数
在(0,+∞)上是增函数,
所以构造函数 例2.比较下列各组数中两个数的大小:当 时方法:①利用对数函数的单调性.
②分类讨论
③用“中间值法”.
构造函数>当 时(4) log56,log65∵构造函数练习三:比较下列各组数中两个数的大小:<<>例3.已知log0.7(3m)
函数的定义域是(0,+∞)。叫做对数函数,其中x是自变量,注:1 、对数函数的定义与指数函数类似,都是形式
定义,注意辨别。2 、对数函数对底数的限制: (a?0,且a ?1)(a?0,且a ?1)一般地,我们把课堂小结:这节课你学到了什么?2.对数函数的图象和性质
(0,+∞)过点(1,0),即当x=1时,y=0 增减1 3.已知函数( -1,3]1.函数 的定义域为 。 2. 比较大小:1) log23 log23.5
2) log0.71.6 log0.71.8< >巩固练习:2.思考:对数函数:y = loga x (a>0,且a≠ 1) 图象随着a取值变化图象如何变化?有规律吗?规律:在x轴
上方图象自左
向右底数越来
越大!x作业: 1.教材P104 A组T2 B组T1Clog,log,log,log则下列式子中正确的是( )的图像如图所示, 3.函数xyxyxyx ydcba=== =再 见
