2.3.3 直线与圆的位置关系 课件(28张PPT)
文档属性
| 名称 | 2.3.3 直线与圆的位置关系 课件(28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 321.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-21 20:29:50 | ||
图片预览






文档简介
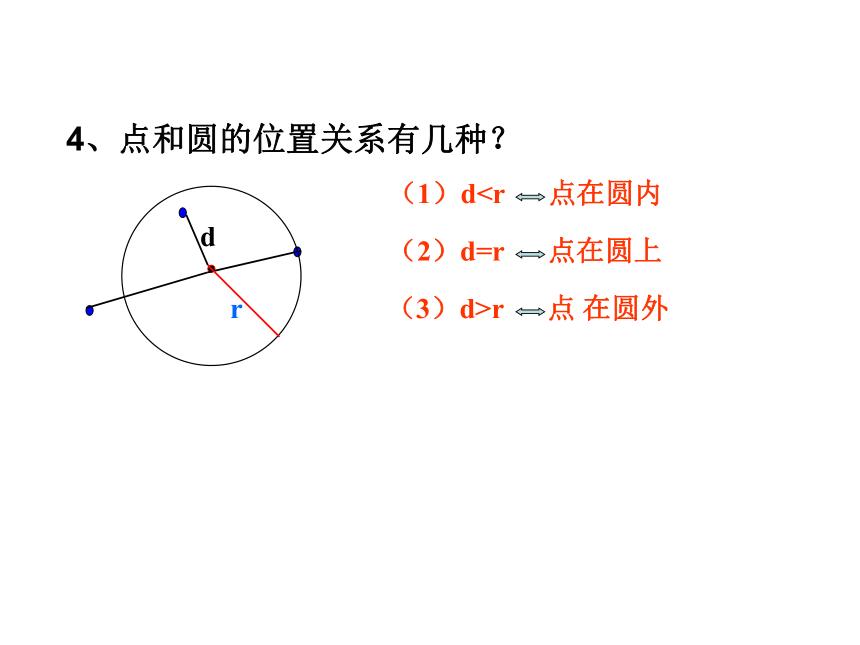
课件28张PPT。“大漠孤烟直,长河落日圆” 是唐朝诗人王维的诗句,它描述了黄昏日落时分塞外特有的景象。如果我们把地平线看成一条直线,太阳看成一个圆,
那你能想象一下,直线和圆的位置关系有几种?
新课导入:1、理解直线和圆相交、相切、相离三种位置关系;
2、掌握直线和圆位置关系的判定方法,并应用其解决问题;
3、掌握求弦长的方法。学习目标: 1、点到直线的距离公式:
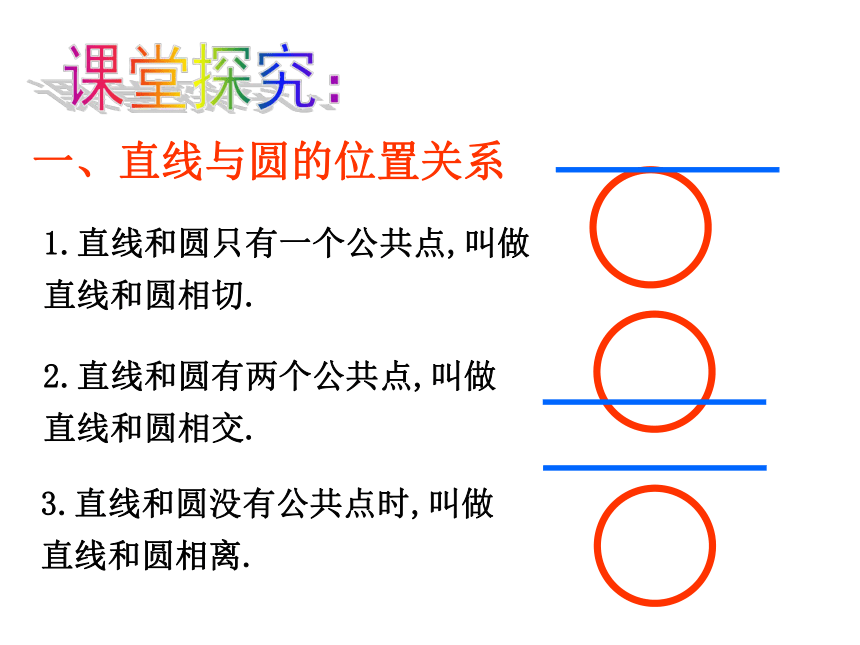
复习回顾: 2、圆的标准方程: 3、圆的一般方程: 4、点和圆的位置关系有几种?rd1.直线和圆只有一个公共点,叫做直线和圆相切.2.直线和圆有两个公共点,叫做
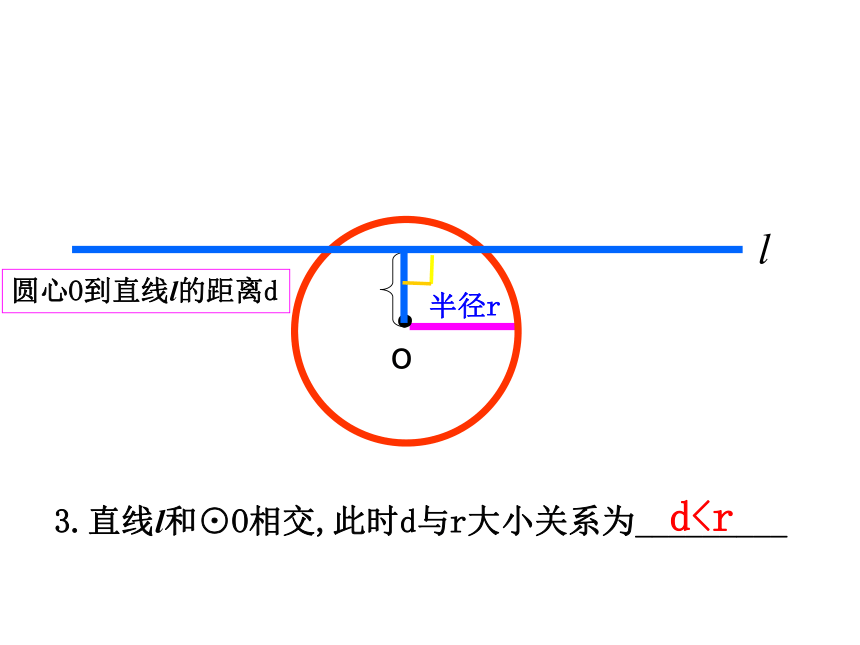
直线和圆相交.3.直线和圆没有公共点时,叫做直线和圆相离.一、直线与圆的位置关系课堂探究:o圆心O到直线l的距离dl半径r1.直线l和⊙O相离,此时d与r大小关系为_________d>ro半径r2.直线l和⊙O相切,此时d与r大小关系为_________d=ro半径r3.直线l和⊙O相交,此时d与r大小关系为_________dA(2,0),B(1,3).如果相交,求它们交点的坐标.直线x+ y=0绕原点按顺时针方向旋转30°所得直线与圆x2+y2-4x+1=0的位置关系是( )
A.直线与圆相切
B.直线与圆相交但不过圆心
C.直线与圆相离
D.直线过圆心【变式练习】A解:选A.因为直线x+ y=0的倾斜角为150°,
所以顺时针方向旋转30°后的倾斜角为120°,
所以旋转后的直线方程为 x+y=0.
将圆的方程化为(x-2)2+y2=3,
所以圆心的坐标为(2,0),半径为 ,圆心到直线 x+y=0的距离为 =圆的半径,
所以直线和圆相切.弦长问题:
例2 :已知过点M(-3,-3)的直线l被圆x2+y2+4y-21=0
所截得的弦长为 ,求直线l的方程.解:将圆的方程写成标准形式,得x2+(y+2)2=25,
所以,圆心的坐标是(0,-2),半径长r=5.
如图,因为直线l被圆所截得
的弦长是 ,所以弦心距为
即圆心到所求直线l的距离为 . 因为直线l过点M(-3,-3),所以可设所求直线l的方程为y+3=k(x+3),即kx-y+3k-3=0.
根据点到直线的距离公式,得到圆心到直线l的距离 因此,即
两边平方,并整理得到 2k2-3k-2=0,
解得k= ,或k=2.
所以,所求直线l有两条,它们的方程分别为
y+3= (x+3),或 y+3=2(x+3).
即x+2y+9=0,或2x-y+3=0.【变式练习】1.设直线过点(0,a),其斜率为1,且与圆x2+y2=2
相切,则a的值为( )
A.± B.±2 C.±2 D.±4【解析】选B.由已知可知直线方程为y=x+a,
即x-y+a=0,所以有 得a=±2.1.⊙O的半径为3 ,圆心O到直线l的距离为d,若直线l
与⊙O没有公共点,则d为( )
A.d >3 B.d<3 C.d ≤3 D.d =3
2.圆心O到直线的距离等于⊙O的半径,则直线和⊙O
的位置关系是( )
A.相离 B.相交 C.相切 D.相切或相交 AC课堂训练:A5.直线x+2y-1=0和圆x2-2x+y2-y+1=0的位置关系是
______.相交4.直线x-y-2=0与圆(x-1)2+(y-1)2=1的位置关系为________.相离6.圆心为M(3,-5),且与直线x-7y+2=0相切的圆的方程为 .(x-3)2+(y+5)2=327.判断直线 与圆 的位置关系. 直线Ax+By+C=0(A,B不同时为零)和圆(x-a)2+(y-b)2=r2,则圆心(a,b)到此直线的距离为drd与r2个1个0个交点个数图形相交相切相离位置rdrdrd则有以下关系:课堂小结求圆心坐标及半径r(配方法) 圆心到直线的距离d (点到直线距离公式) 消去y判断直线和圆的位置关系几何方法代数方法 第101页练习A、练习B课后作业:
2、掌握直线和圆位置关系的判定方法,并应用其解决问题;
3、掌握求弦长的方法。学习目标: 1、点到直线的距离公式:
复习回顾: 2、圆的标准方程: 3、圆的一般方程: 4、点和圆的位置关系有几种?rd1.直线和圆只有一个公共点,叫做直线和圆相切.2.直线和圆有两个公共点,叫做
直线和圆相交.3.直线和圆没有公共点时,叫做直线和圆相离.一、直线与圆的位置关系课堂探究:o圆心O到直线l的距离dl半径r1.直线l和⊙O相离,此时d与r大小关系为_________d>ro半径r2.直线l和⊙O相切,此时d与r大小关系为_________d=ro半径r3.直线l和⊙O相交,此时d与r大小关系为_________d
A.直线与圆相切
B.直线与圆相交但不过圆心
C.直线与圆相离
D.直线过圆心【变式练习】A解:选A.因为直线x+ y=0的倾斜角为150°,
所以顺时针方向旋转30°后的倾斜角为120°,
所以旋转后的直线方程为 x+y=0.
将圆的方程化为(x-2)2+y2=3,
所以圆心的坐标为(2,0),半径为 ,圆心到直线 x+y=0的距离为 =圆的半径,
所以直线和圆相切.弦长问题:
例2 :已知过点M(-3,-3)的直线l被圆x2+y2+4y-21=0
所截得的弦长为 ,求直线l的方程.解:将圆的方程写成标准形式,得x2+(y+2)2=25,
所以,圆心的坐标是(0,-2),半径长r=5.
如图,因为直线l被圆所截得
的弦长是 ,所以弦心距为
即圆心到所求直线l的距离为 . 因为直线l过点M(-3,-3),所以可设所求直线l的方程为y+3=k(x+3),即kx-y+3k-3=0.
根据点到直线的距离公式,得到圆心到直线l的距离 因此,即
两边平方,并整理得到 2k2-3k-2=0,
解得k= ,或k=2.
所以,所求直线l有两条,它们的方程分别为
y+3= (x+3),或 y+3=2(x+3).
即x+2y+9=0,或2x-y+3=0.【变式练习】1.设直线过点(0,a),其斜率为1,且与圆x2+y2=2
相切,则a的值为( )
A.± B.±2 C.±2 D.±4【解析】选B.由已知可知直线方程为y=x+a,
即x-y+a=0,所以有 得a=±2.1.⊙O的半径为3 ,圆心O到直线l的距离为d,若直线l
与⊙O没有公共点,则d为( )
A.d >3 B.d<3 C.d ≤3 D.d =3
2.圆心O到直线的距离等于⊙O的半径,则直线和⊙O
的位置关系是( )
A.相离 B.相交 C.相切 D.相切或相交 AC课堂训练:A5.直线x+2y-1=0和圆x2-2x+y2-y+1=0的位置关系是
______.相交4.直线x-y-2=0与圆(x-1)2+(y-1)2=1的位置关系为________.相离6.圆心为M(3,-5),且与直线x-7y+2=0相切的圆的方程为 .(x-3)2+(y+5)2=327.判断直线 与圆 的位置关系. 直线Ax+By+C=0(A,B不同时为零)和圆(x-a)2+(y-b)2=r2,则圆心(a,b)到此直线的距离为d
