人教A版数学选修2—1 3.2 立体几何中的向量方法(二)空间角(共19张ppt)
文档属性
| 名称 | 人教A版数学选修2—1 3.2 立体几何中的向量方法(二)空间角(共19张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-21 21:11:03 | ||
图片预览





文档简介
课件19张PPT。立体几何中的
向量方法(二)
空间角教学目标1.知识与技能
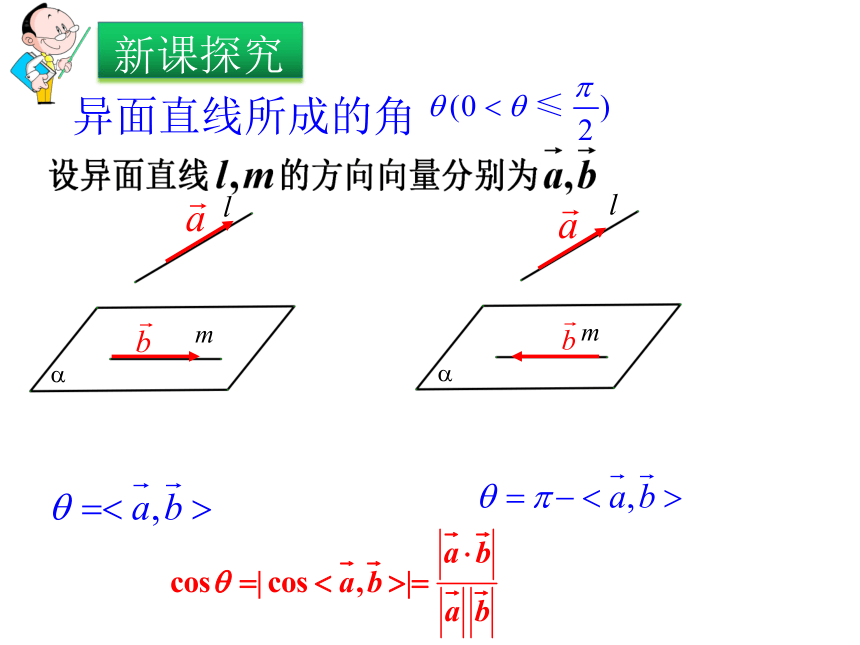
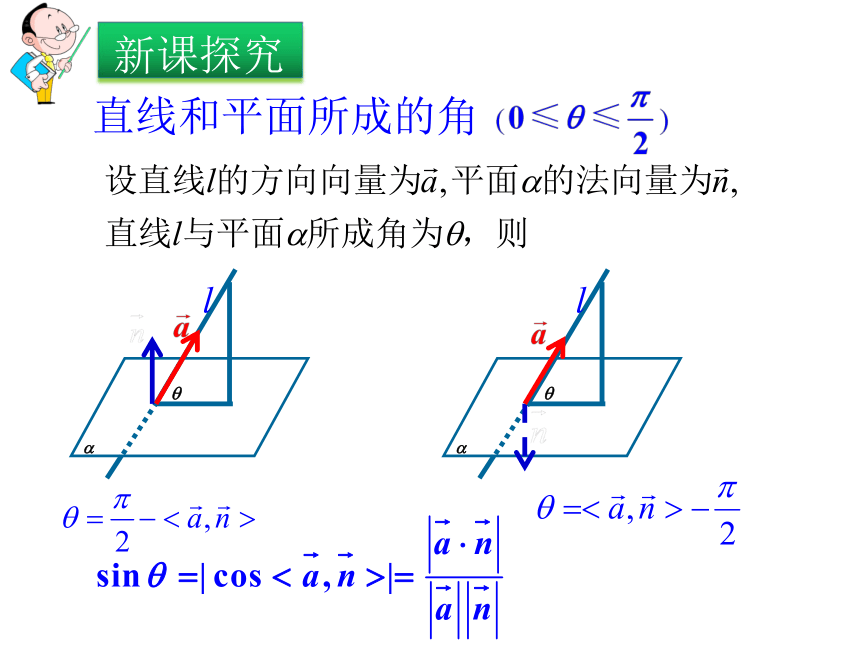
1)使学生学会求异面直线所成的角、直线与平面所成的角、二面角的向量方法 ;
2)能利用空间向量解决关于角的问题;
2.过程与方法 经历用向量解决某些问题,体会向量
是一种处理几何问题的工具;
3.情感、态度与价值观 通过本节课的学习,体验创造的激情,培养学生发现、提出、解决问题的能力用空间向量解决立体几何问题的三步曲:1.(化为向量问题)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题.
2.(进行向量运算)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间距离和夹角等问题.
3.(回到图形问题)把向量的运算结果“翻译”成相应的几何意义.解决立体几何中的问题可用三种方法:综合法、向量法、坐标法异面直线所成的角直线和平面所成的角法一综合法法二坐标法 平面和平面所成的角---二面角设a —l —b的平面角为q设a —l —b的平面
角为qq =g法一综合法法二向量法法三坐标法课堂小结一、求空间角的方法:综合法,向量法,坐标法二、利用向量求空间角
向量方法(二)
空间角教学目标1.知识与技能
1)使学生学会求异面直线所成的角、直线与平面所成的角、二面角的向量方法 ;
2)能利用空间向量解决关于角的问题;
2.过程与方法 经历用向量解决某些问题,体会向量
是一种处理几何问题的工具;
3.情感、态度与价值观 通过本节课的学习,体验创造的激情,培养学生发现、提出、解决问题的能力用空间向量解决立体几何问题的三步曲:1.(化为向量问题)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题.
2.(进行向量运算)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间距离和夹角等问题.
3.(回到图形问题)把向量的运算结果“翻译”成相应的几何意义.解决立体几何中的问题可用三种方法:综合法、向量法、坐标法异面直线所成的角直线和平面所成的角法一综合法法二坐标法 平面和平面所成的角---二面角设a —l —b的平面角为q设a —l —b的平面
角为qq =g法一综合法法二向量法法三坐标法课堂小结一、求空间角的方法:综合法,向量法,坐标法二、利用向量求空间角
