1.1.7 柱、锥、台和球的体积 课件(20张)
文档属性
| 名称 | 1.1.7 柱、锥、台和球的体积 课件(20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 455.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-21 23:04:29 | ||
图片预览








文档简介
课件20张PPT。1.1.7 柱、锥、台和球的体积普通高中课程标准实验教科书数学必修2(人教B版)1.1 空间几何体学习目标:
1.通过对柱、锥、台体的研究,掌握柱、锥、台的体积的计算方法;
2.了解球的体积公式;
3.理解祖暅原理及其在公式推导中的作用。体积是指物体所占空间的大小。你认识下列几何体吗?那么如何计算它们的体积呢?取一摞大小相同的课本放在桌面上(如图所示) ,并改变它们的放置方法,思考下列问题:实验探究问题:(1)倾斜前后这摞课本的总高度是否发生了变化? (2)倾斜前后等高处的每一张纸的面积是否发生了变化?(3)倾斜前后这摞课本的体积是否发生了变化?结论:两个等高的几何体若在所有等高处的水平
截面的面积总相等,则这两个几何体的体积相等。事实上,夹在两个平行平面间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等。幂势既同,则积不容异祖暅原理祖暅原理:幂势既同,则积不容异。水平截面面积高体积+说明:
等底面积、等高的两个柱体或锥体的体积相等。 祖暅原理是推导柱、锥、台和球体积公式的基础和纽带,原理中含有三个条件:
条件一是两个几何体夹在两个平行平面之间;
条件二是用平行于两个平行平面的任何一平面可截得两个截面;
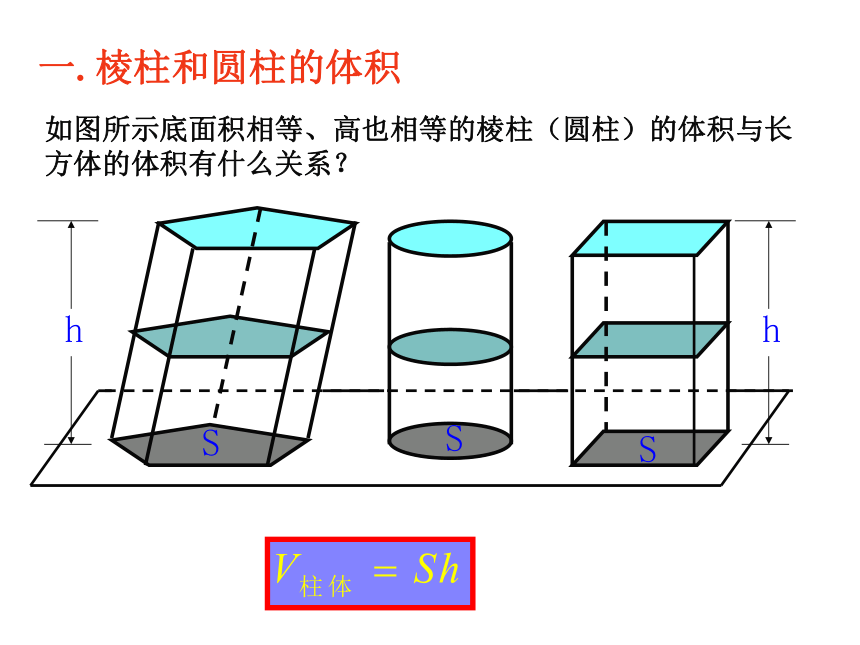
条件三是两个截面的面积总相等,这三个条件缺一不可,否则结论不成立. 祖暅,祖冲之之子,圆满解决了球面积的计算问题,得到正确的体积公式。祖暅总结了刘徽的有关工作,提出“幂势既同则积不容异”,即等高的两立体,若其任意高处的水平截面积相等,则这两立体体积相等,这就是著名的“祖暅原理” (或刘祖原理)。祖暅应用这个原理,解决了刘徽尚未解决的球体积公式。该原理在西方直到十七世纪才由意大利数学家卡瓦列利发现,比祖暅晚一千一百多年。祖暅的儿子祖皓,续传家学,后来也成了数学家。祖冲之名人博览祖暅SSS如图所示底面积相等、高也相等的棱柱(圆柱)的体积与长方体的体积有什么关系?一. 棱柱和圆柱的体积 二. 棱锥和圆锥的体积 三. 棱台和圆台的体积 柱体、锥体、台体的体积公式间的关系形数四. 球的体积 例4.如图是一个奖杯的三视图,(单位:cm)试计算这个奖杯的体积课堂小结1、知识:2、方法:(1)祖暅原理(2)柱、锥、台和球的体积类比 转化1. 一个正方体的棱长为1,它的各个顶点都在同一个球面上,求该球的体积。2.如图,是一个几何体的三视图,则该几何体的体积为 ( )当堂检测
1.通过对柱、锥、台体的研究,掌握柱、锥、台的体积的计算方法;
2.了解球的体积公式;
3.理解祖暅原理及其在公式推导中的作用。体积是指物体所占空间的大小。你认识下列几何体吗?那么如何计算它们的体积呢?取一摞大小相同的课本放在桌面上(如图所示) ,并改变它们的放置方法,思考下列问题:实验探究问题:(1)倾斜前后这摞课本的总高度是否发生了变化? (2)倾斜前后等高处的每一张纸的面积是否发生了变化?(3)倾斜前后这摞课本的体积是否发生了变化?结论:两个等高的几何体若在所有等高处的水平
截面的面积总相等,则这两个几何体的体积相等。事实上,夹在两个平行平面间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等。幂势既同,则积不容异祖暅原理祖暅原理:幂势既同,则积不容异。水平截面面积高体积+说明:
等底面积、等高的两个柱体或锥体的体积相等。 祖暅原理是推导柱、锥、台和球体积公式的基础和纽带,原理中含有三个条件:
条件一是两个几何体夹在两个平行平面之间;
条件二是用平行于两个平行平面的任何一平面可截得两个截面;
条件三是两个截面的面积总相等,这三个条件缺一不可,否则结论不成立. 祖暅,祖冲之之子,圆满解决了球面积的计算问题,得到正确的体积公式。祖暅总结了刘徽的有关工作,提出“幂势既同则积不容异”,即等高的两立体,若其任意高处的水平截面积相等,则这两立体体积相等,这就是著名的“祖暅原理” (或刘祖原理)。祖暅应用这个原理,解决了刘徽尚未解决的球体积公式。该原理在西方直到十七世纪才由意大利数学家卡瓦列利发现,比祖暅晚一千一百多年。祖暅的儿子祖皓,续传家学,后来也成了数学家。祖冲之名人博览祖暅SSS如图所示底面积相等、高也相等的棱柱(圆柱)的体积与长方体的体积有什么关系?一. 棱柱和圆柱的体积 二. 棱锥和圆锥的体积 三. 棱台和圆台的体积 柱体、锥体、台体的体积公式间的关系形数四. 球的体积 例4.如图是一个奖杯的三视图,(单位:cm)试计算这个奖杯的体积课堂小结1、知识:2、方法:(1)祖暅原理(2)柱、锥、台和球的体积类比 转化1. 一个正方体的棱长为1,它的各个顶点都在同一个球面上,求该球的体积。2.如图,是一个几何体的三视图,则该几何体的体积为 ( )当堂检测
