1.3 中国古代数学中的算法案例 课件(21张PPT)
文档属性
| 名称 | 1.3 中国古代数学中的算法案例 课件(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 216.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-23 08:53:16 | ||
图片预览







文档简介
课件21张PPT。北京市石景山区首钢矿业职工子弟学校一师一优课1.3 中国古代数学中的算法案例刘徽割圆术了解中国古代数学的成就及与西方数学的
差异。
2. 能说出刘徽割圆术的基本思想,理解割圆
术的算法。
3. 能用Scilab语言设计求圆周率的近似值的
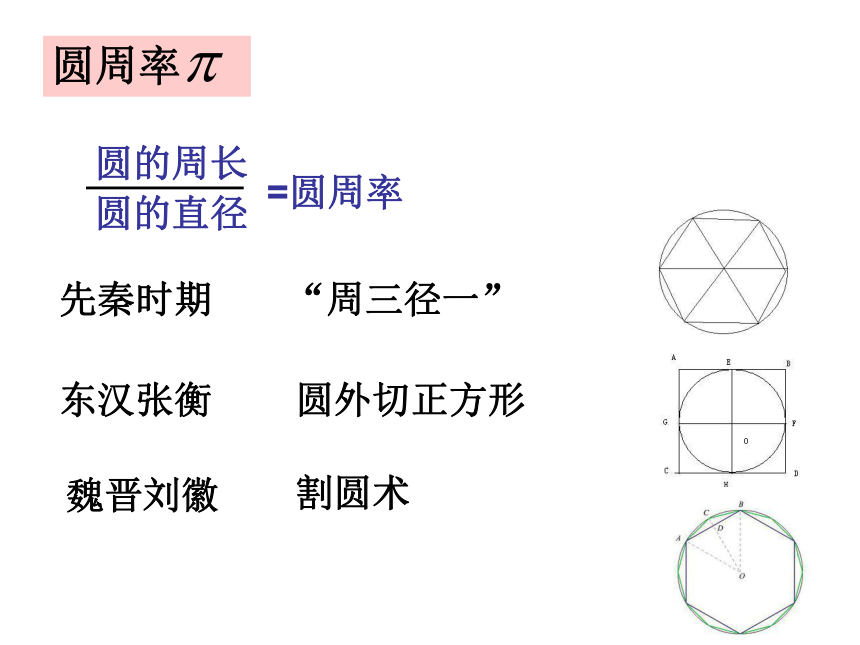
程序。学习目标:如何度量曲边图形的周长和面积中国古代数学与西方数学的差异西方数学中国古代数学从公理出发,主要内容是证明公理从问题出发,主要内容是解方程 中国古代数学着重计算,要把计算的过程、方法、步骤说出来。这个方法步骤,用现代的话来讲,就相当于所谓的算法。 中国的古代数学是一种算法的数学,也就是一种计算机的数学。从这个意义上来讲,我们最古老的数学也是计算机时代最适合、最现代的数学。------节选自吴文俊《东方数学的使命》圆周率先秦时期“周三径一”东汉张衡圆外切正方形魏晋刘徽割圆术刘徽割圆术1.基本思想割之弥细
失之弥少
割之弥细
失之弥少
割之又割
以至于不可割
则与圆合体
而无所失矣不可
则与圆合体
而无所失矣2.割圆术算法研究以直代曲,无限逼近2.割圆术算法研究……计算的递推问题1:
假定圆的半径为1,那么圆的面积是多少?
圆内接正六边形的边长和面积分别是多少?数据分析问题2:
如何由圆内接正六边形边长和面积去求圆内接正十二边形的面积和边长?
(只研究方法,不必计算)数据分析思考:计算的递推靠哪些量来实现?问题3:
若已求得圆内接正n边形边长和面积,如何求圆内接正2n边形的面积和边长?数据分析数据分析已求得圆内接正n边形
边长为
面积为破损的圆外切正n边形高明的逼近方法不足近似值过剩近似值两边夹刘徽圆内接正96边形圆内接正3072边形祖冲之精确到小数点后第7位这一结果的得出比西方早了1100年3.动手实践几何画板演示请同学们根据刘徽割圆术的算法思想,用Scilab语言写出求 的近似值的程序.
(用圆内接正多边形面积求不足近似值)提示:以半径为1的圆内接正六边形边长和面积为初值,利用计算的递推来设计程序,要求输出结果中显示出面积和正多边形边数。初值
边数边长面积递推关系总结提升1.刘徽割圆术
基本思想: 以圆内接正多边形面积逼近
圆的面积算法特点:2.刘徽割圆术蕴含的数学思想:
以直代曲、无限逼近课后作业1. 从不同角度设计求圆周率的程序并计算机
验证。
2.查阅资料,了解圆周率在世界各国的发展
史或圆周率的其他算法,写成小论文。
(不少于500字)n=6;
x=1;
c=input("次数=");
s=6*sqrt(3)/4;
for i=1:1:c
h=sqrt(1-(x/2)^2);
s=s+n*x*(1-h)/2;
n=2*n;
x=sqrt((x/2)^2+(1-h)^2);
end
print(%io(2),n,s);
差异。
2. 能说出刘徽割圆术的基本思想,理解割圆
术的算法。
3. 能用Scilab语言设计求圆周率的近似值的
程序。学习目标:如何度量曲边图形的周长和面积中国古代数学与西方数学的差异西方数学中国古代数学从公理出发,主要内容是证明公理从问题出发,主要内容是解方程 中国古代数学着重计算,要把计算的过程、方法、步骤说出来。这个方法步骤,用现代的话来讲,就相当于所谓的算法。 中国的古代数学是一种算法的数学,也就是一种计算机的数学。从这个意义上来讲,我们最古老的数学也是计算机时代最适合、最现代的数学。------节选自吴文俊《东方数学的使命》圆周率先秦时期“周三径一”东汉张衡圆外切正方形魏晋刘徽割圆术刘徽割圆术1.基本思想割之弥细
失之弥少
割之弥细
失之弥少
割之又割
以至于不可割
则与圆合体
而无所失矣不可
则与圆合体
而无所失矣2.割圆术算法研究以直代曲,无限逼近2.割圆术算法研究……计算的递推问题1:
假定圆的半径为1,那么圆的面积是多少?
圆内接正六边形的边长和面积分别是多少?数据分析问题2:
如何由圆内接正六边形边长和面积去求圆内接正十二边形的面积和边长?
(只研究方法,不必计算)数据分析思考:计算的递推靠哪些量来实现?问题3:
若已求得圆内接正n边形边长和面积,如何求圆内接正2n边形的面积和边长?数据分析数据分析已求得圆内接正n边形
边长为
面积为破损的圆外切正n边形高明的逼近方法不足近似值过剩近似值两边夹刘徽圆内接正96边形圆内接正3072边形祖冲之精确到小数点后第7位这一结果的得出比西方早了1100年3.动手实践几何画板演示请同学们根据刘徽割圆术的算法思想,用Scilab语言写出求 的近似值的程序.
(用圆内接正多边形面积求不足近似值)提示:以半径为1的圆内接正六边形边长和面积为初值,利用计算的递推来设计程序,要求输出结果中显示出面积和正多边形边数。初值
边数边长面积递推关系总结提升1.刘徽割圆术
基本思想: 以圆内接正多边形面积逼近
圆的面积算法特点:2.刘徽割圆术蕴含的数学思想:
以直代曲、无限逼近课后作业1. 从不同角度设计求圆周率的程序并计算机
验证。
2.查阅资料,了解圆周率在世界各国的发展
史或圆周率的其他算法,写成小论文。
(不少于500字)n=6;
x=1;
c=input("次数=");
s=6*sqrt(3)/4;
for i=1:1:c
h=sqrt(1-(x/2)^2);
s=s+n*x*(1-h)/2;
n=2*n;
x=sqrt((x/2)^2+(1-h)^2);
end
print(%io(2),n,s);
