2.1.3 分层抽样 课件(18张PPT)
文档属性
| 名称 | 2.1.3 分层抽样 课件(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 82.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-23 00:00:00 | ||
图片预览






文档简介
课件18张PPT。数学必修3分层抽样 复习回顾 简单随机抽样的特点是什么?简单随机抽样:如果用从个体数为N的总体中抽取一个容量为n的样本,那么每个个体被抽取的概卒等于 抽签法 随机抽样的方法:随机数表法抽签法第一步,将总体中的N个个体编号(号码从1到N);并把号码写在形状、大小相 同的号签上;第二步,将号签放在一个不透明 容器中,并搅拌均匀;第三步,每次抽出1个号签,连续抽取n次,就得到一个容量为n的样本复习回顾 复习回顾 系统抽样的特点是什么?系统抽样:
①编号,分段,定起始号,抽取;②等可能抽样;
③总体容量较大。
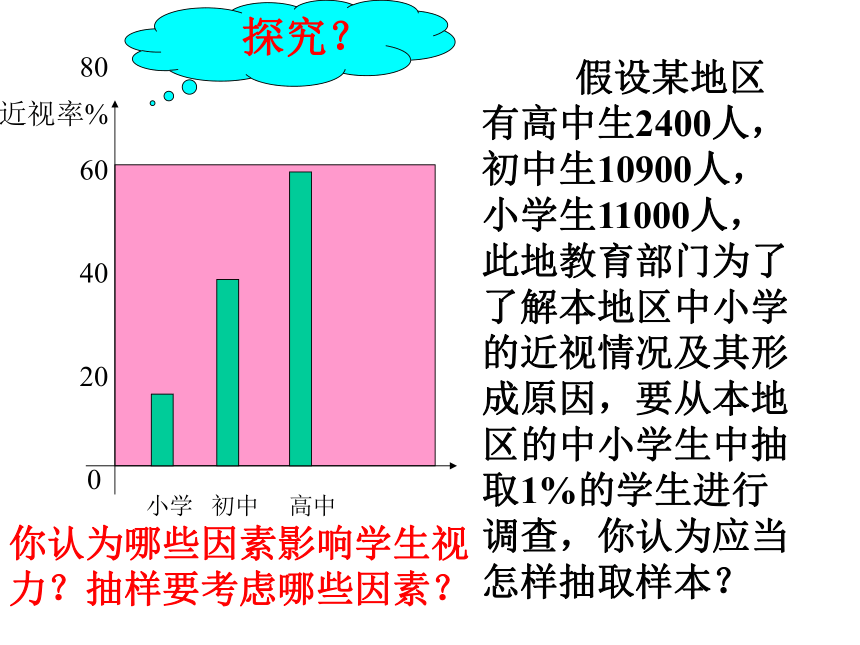
系统抽样时,将总体中的个体均分后的每一段进行抽样时,采用简单随机抽样;系统抽样每次抽样时,总体中各个个体被抽取的概率也是相等的;如总体的个体数不能被样本容量整除时,可以先用简单随机抽样从总体中剔除几个个体,然后再按系统抽样进行。需要说明的是整个抽样过程中每个个体被抽到的概率仍然相等。 假设某地区有高中生2400人,初中生10900人,小学生11000人,此地教育部门为了了解本地区中小学的近视情况及其形成原因,要从本地区的中小学生中抽取1%的学生进行调查,你认为应当怎样抽取样本?你认为哪些因素影响学生视力?抽样要考虑哪些因素? 某地区有高中生2400人,初中生10900人,小学生11100人,当地教育部门为了了解本地区中小学生的近视率及其形成原因,要从本地区的中小学生中抽取1%的学生进行调查。你认为应当如何抽取样本?
分析:不同年龄阶段的学生的近视情况可能存在明 显差异,因此,宜将全体学生分成高中、初中和小学三部分分别抽样。另外,三部分的学生人数相差较大,因此,为了提高样本的代表性,还应考虑他们在样本中所占比例的大小。探究 某地区有高中生2400人,初中生10900人,小学生11100人,当地教育部门为了了解本地区中小学生的近视率及其形成原因,要从本地区的中小学生中抽取1%的学生进行调查。你认为应当如何抽取样本?
由于样本容量与总体个体数之比为1:100,因此,样本中包含的各部门的个体数应该是:
即抽取24名高中生,109名初中生和110名小学生作为样本。探究一般的,在抽样时,将总体分成互不交叉的层,然后按照一定的比例,从各层独立地抽取一定数量的个体,将各层取出的个体合在一起作为样本,这种抽样的方法叫分层抽样.分层抽样 分层抽样是当总体由 的几部分组成时采用的抽样方法,进行分层抽样时应注意以下几点:(1)分层时将相似的个体归入一类,即为一层,分层要求每层的个体互不交叉,即遵循不重复不遗漏的原则,即保证 与 一致性。(3)在每层抽样时,应采用______________________ 的方法进行抽样。差异明显总体结构 样本结构(2)为了保证每个个体等可能入样,所有层应
采用同一 等可能抽样。抽样比简单随机抽样或系统抽 样分层抽样的具体步骤是什么? 步骤1:根据已经掌握的信息,将总体分成互不相交的层
步骤2:根据总体的个体数N和样本容量n计算抽样比k=n:N步骤3:确定每一层应抽取的个体数目,使得每一层应抽取的个体数目之和为样本容量n步骤4:按步骤3确定的数目在各层中随机抽取个体,合在一起得到容量为n样本分层求比定数抽样知识点一 分层抽样的概念
例1 某社区有700户家庭,其中高收入家庭225户,中等收入家庭400户,低收入家庭75户,为了调查社会购买力的某项指标,要从中抽取一个容量为100户的样本,记作①;某中学高二年级有12名足球运动员,要从中选出3人调查学习负担情况,记②;从某厂生产的802辆轿车中抽取8辆测试某项性能,记作③.则完成上述3项应采用的抽样方法是 ( )
A.①用简单随机抽样,②用系统抽样,③用分层抽样
B.①用分层抽样,②用简单随机抽样,③用系统抽样
C.①用简单随机抽样,②用分层抽样,③用系统抽样
D.①用分层抽样,②用系统抽样,③用简单随机抽样B例2、某中学高中学生有900名.为了考察他们的体重状况,打算抽取容量为45的一个样本.已知高一有400名学生,高二有300名学生,高三有200名学生,应如何抽取? 分析:这总体具有某些特征,它可以分成几个不同的部分:高一;高二;高三,把每一部分称为一个层,因此该总体可以分为3个层。由于抽取的样本为45,所以必须确定每一层的比例,在每一个层中实行简单随机抽样。 解:抽取人数与学生总数的比是45:900=1:20,则各年级(层)的学生人数依次是20 15 10,然后分别在各年级(层)运用简单随机抽样方法抽取。
答:在分层抽样时,高一、高二、高三分别抽取学生20人、15人和10人。知识点二 分层抽样的应用例2、某中学高中学生有900名.为了考察他们的体重状况,打算抽取容量为45的一个样本.已知高一有402名学生,高二有296名学生,高三有202名学生,应如何抽取? 解:抽取人数与学生总数的比是45:900=1:20,则各年级(层)的学生人数依次是20.1 14.8 10.1.
变式探究 注:每个层面上抽取的学生数用除法算出的结果不是整数时,可作适当的微调整,使抽取的学生数为整数。
故各年级(层)的学生人数依次是20 15 10.
适应范围相互联系抽样特征 共同
特点 方法
类别简单随
机抽样系统
抽样分层
抽样抽样过程中每个个体被抽取的概率相等将总体均匀分成几个部分,按事先确定的规则在各部分抽取将总体分成几层,按比例分层抽取在起始部分抽样时采用简单随机抽样总体中的个体数较少总体中的个体数较多总体由差异明显的几部分组成从总体中逐个不放回抽取用简单随机抽样或系统抽样对各层抽样某市有300所小学,共有240000名学生,这些小学分布在全市5个行政区中,其中重点小学有30所,一般小学有240所,较差的小学有30所。现在要从全市小学生中抽取1200名学生进行调查,以了解全市小学生的学习情况。请设计一份抽样方案。创新设计分层抽样方案:
1、因为有300所小学,240000名学生,假设每所小学的学生人数相同,所以每所小学有学生人数800名。
2、又因为有重点小学30所,一般小学240所,较差小学30所,所以重点小学有学生人数24000名,一般小学有学生人数192000名,较差小学有学生人数24000名。
3、因为要从240000名学生中抽取1200名学生进行调查,所以1200:240000=1:200,即每200名学生中抽取1名学生进行调查,所以由第2步得出24000×1/200=120名;192000×1/200=960名;24000×1/200=120名,然后按照简单随机抽样的方法分别抽取相应的人数。
4、综上所述,要从240000名学生中抽取1200名学生进行调查,应当从30所重点小学中抽取120名学生,从240所一般小学中抽取960名学生,从30所较差小学中抽取120名学生,共计1200名学生。
你的创新设计呢? 某中学有高一学生400人,高二学 生302人,
高三学生250人,先要用分层抽样的方法从全校中抽取一个容量为190人的样本,应剔除几人?每个年级应分别抽取多少人?
要求:写出具体的分层抽样步骤作业
①编号,分段,定起始号,抽取;②等可能抽样;
③总体容量较大。
系统抽样时,将总体中的个体均分后的每一段进行抽样时,采用简单随机抽样;系统抽样每次抽样时,总体中各个个体被抽取的概率也是相等的;如总体的个体数不能被样本容量整除时,可以先用简单随机抽样从总体中剔除几个个体,然后再按系统抽样进行。需要说明的是整个抽样过程中每个个体被抽到的概率仍然相等。 假设某地区有高中生2400人,初中生10900人,小学生11000人,此地教育部门为了了解本地区中小学的近视情况及其形成原因,要从本地区的中小学生中抽取1%的学生进行调查,你认为应当怎样抽取样本?你认为哪些因素影响学生视力?抽样要考虑哪些因素? 某地区有高中生2400人,初中生10900人,小学生11100人,当地教育部门为了了解本地区中小学生的近视率及其形成原因,要从本地区的中小学生中抽取1%的学生进行调查。你认为应当如何抽取样本?
分析:不同年龄阶段的学生的近视情况可能存在明 显差异,因此,宜将全体学生分成高中、初中和小学三部分分别抽样。另外,三部分的学生人数相差较大,因此,为了提高样本的代表性,还应考虑他们在样本中所占比例的大小。探究 某地区有高中生2400人,初中生10900人,小学生11100人,当地教育部门为了了解本地区中小学生的近视率及其形成原因,要从本地区的中小学生中抽取1%的学生进行调查。你认为应当如何抽取样本?
由于样本容量与总体个体数之比为1:100,因此,样本中包含的各部门的个体数应该是:
即抽取24名高中生,109名初中生和110名小学生作为样本。探究一般的,在抽样时,将总体分成互不交叉的层,然后按照一定的比例,从各层独立地抽取一定数量的个体,将各层取出的个体合在一起作为样本,这种抽样的方法叫分层抽样.分层抽样 分层抽样是当总体由 的几部分组成时采用的抽样方法,进行分层抽样时应注意以下几点:(1)分层时将相似的个体归入一类,即为一层,分层要求每层的个体互不交叉,即遵循不重复不遗漏的原则,即保证 与 一致性。(3)在每层抽样时,应采用______________________ 的方法进行抽样。差异明显总体结构 样本结构(2)为了保证每个个体等可能入样,所有层应
采用同一 等可能抽样。抽样比简单随机抽样或系统抽 样分层抽样的具体步骤是什么? 步骤1:根据已经掌握的信息,将总体分成互不相交的层
步骤2:根据总体的个体数N和样本容量n计算抽样比k=n:N步骤3:确定每一层应抽取的个体数目,使得每一层应抽取的个体数目之和为样本容量n步骤4:按步骤3确定的数目在各层中随机抽取个体,合在一起得到容量为n样本分层求比定数抽样知识点一 分层抽样的概念
例1 某社区有700户家庭,其中高收入家庭225户,中等收入家庭400户,低收入家庭75户,为了调查社会购买力的某项指标,要从中抽取一个容量为100户的样本,记作①;某中学高二年级有12名足球运动员,要从中选出3人调查学习负担情况,记②;从某厂生产的802辆轿车中抽取8辆测试某项性能,记作③.则完成上述3项应采用的抽样方法是 ( )
A.①用简单随机抽样,②用系统抽样,③用分层抽样
B.①用分层抽样,②用简单随机抽样,③用系统抽样
C.①用简单随机抽样,②用分层抽样,③用系统抽样
D.①用分层抽样,②用系统抽样,③用简单随机抽样B例2、某中学高中学生有900名.为了考察他们的体重状况,打算抽取容量为45的一个样本.已知高一有400名学生,高二有300名学生,高三有200名学生,应如何抽取? 分析:这总体具有某些特征,它可以分成几个不同的部分:高一;高二;高三,把每一部分称为一个层,因此该总体可以分为3个层。由于抽取的样本为45,所以必须确定每一层的比例,在每一个层中实行简单随机抽样。 解:抽取人数与学生总数的比是45:900=1:20,则各年级(层)的学生人数依次是20 15 10,然后分别在各年级(层)运用简单随机抽样方法抽取。
答:在分层抽样时,高一、高二、高三分别抽取学生20人、15人和10人。知识点二 分层抽样的应用例2、某中学高中学生有900名.为了考察他们的体重状况,打算抽取容量为45的一个样本.已知高一有402名学生,高二有296名学生,高三有202名学生,应如何抽取? 解:抽取人数与学生总数的比是45:900=1:20,则各年级(层)的学生人数依次是20.1 14.8 10.1.
变式探究 注:每个层面上抽取的学生数用除法算出的结果不是整数时,可作适当的微调整,使抽取的学生数为整数。
故各年级(层)的学生人数依次是20 15 10.
适应范围相互联系抽样特征 共同
特点 方法
类别简单随
机抽样系统
抽样分层
抽样抽样过程中每个个体被抽取的概率相等将总体均匀分成几个部分,按事先确定的规则在各部分抽取将总体分成几层,按比例分层抽取在起始部分抽样时采用简单随机抽样总体中的个体数较少总体中的个体数较多总体由差异明显的几部分组成从总体中逐个不放回抽取用简单随机抽样或系统抽样对各层抽样某市有300所小学,共有240000名学生,这些小学分布在全市5个行政区中,其中重点小学有30所,一般小学有240所,较差的小学有30所。现在要从全市小学生中抽取1200名学生进行调查,以了解全市小学生的学习情况。请设计一份抽样方案。创新设计分层抽样方案:
1、因为有300所小学,240000名学生,假设每所小学的学生人数相同,所以每所小学有学生人数800名。
2、又因为有重点小学30所,一般小学240所,较差小学30所,所以重点小学有学生人数24000名,一般小学有学生人数192000名,较差小学有学生人数24000名。
3、因为要从240000名学生中抽取1200名学生进行调查,所以1200:240000=1:200,即每200名学生中抽取1名学生进行调查,所以由第2步得出24000×1/200=120名;192000×1/200=960名;24000×1/200=120名,然后按照简单随机抽样的方法分别抽取相应的人数。
4、综上所述,要从240000名学生中抽取1200名学生进行调查,应当从30所重点小学中抽取120名学生,从240所一般小学中抽取960名学生,从30所较差小学中抽取120名学生,共计1200名学生。
你的创新设计呢? 某中学有高一学生400人,高二学 生302人,
高三学生250人,先要用分层抽样的方法从全校中抽取一个容量为190人的样本,应剔除几人?每个年级应分别抽取多少人?
要求:写出具体的分层抽样步骤作业
