2.3.2 两个变量的线性相关 课件(22张PPT)
文档属性
| 名称 | 2.3.2 两个变量的线性相关 课件(22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-23 09:01:28 | ||
图片预览




文档简介
课件22张PPT。
课题:两个变量的线性相关
高一年级
人教B版必修3
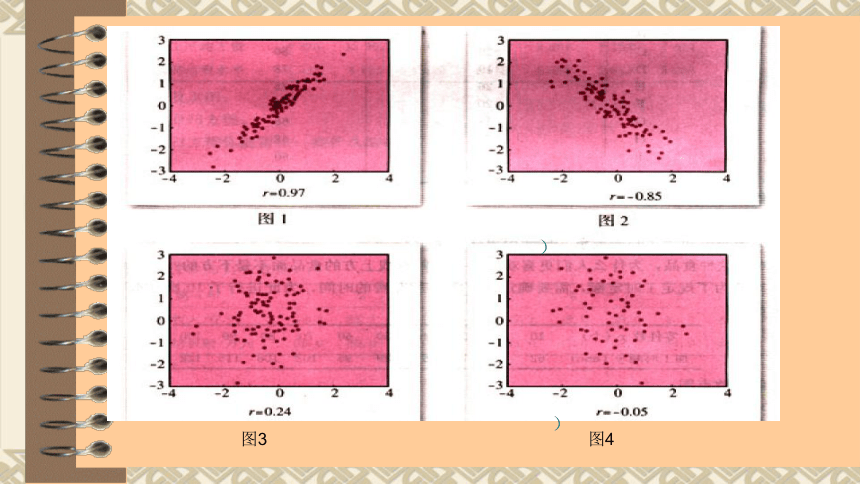
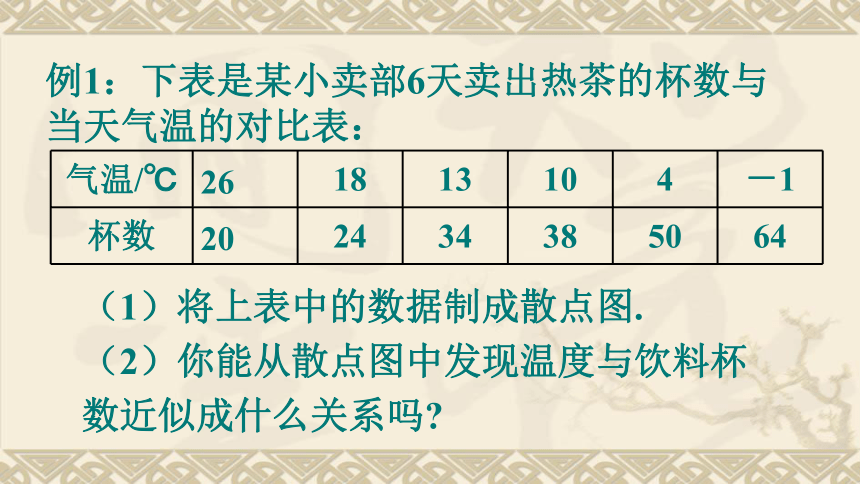
))图3图4例1:下表是某小卖部6天卖出热茶的杯数与当天气温的对比表: (1)将上表中的数据制成散点图.
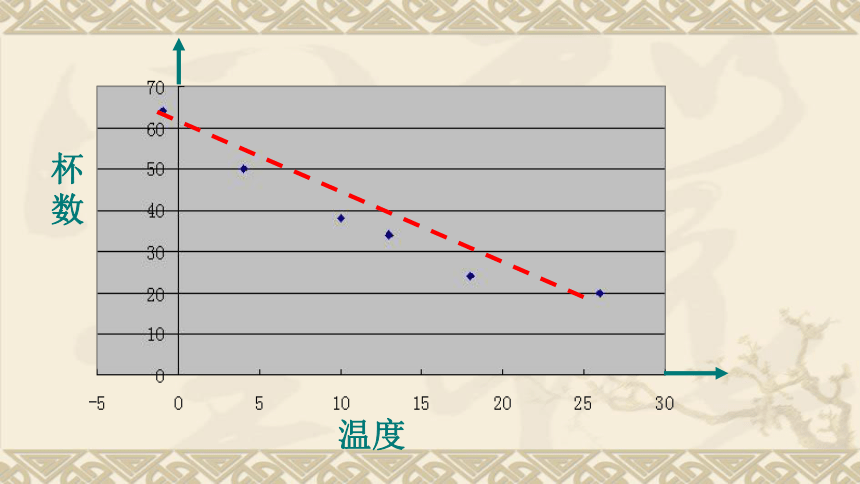
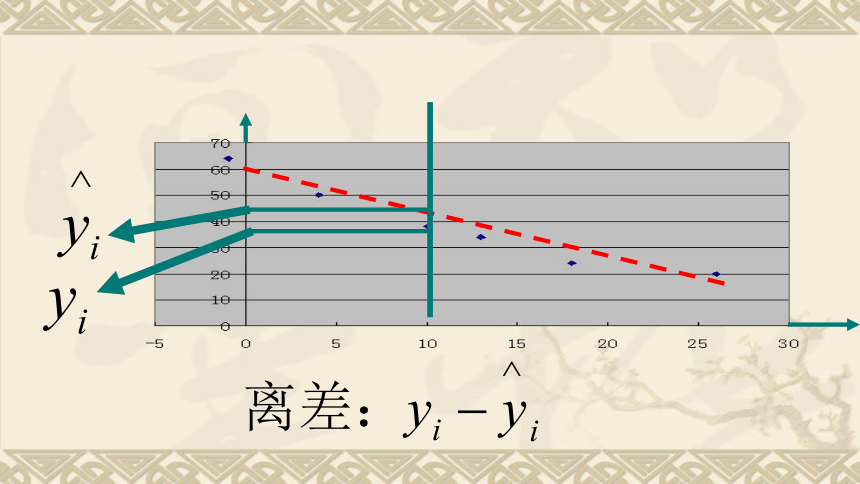
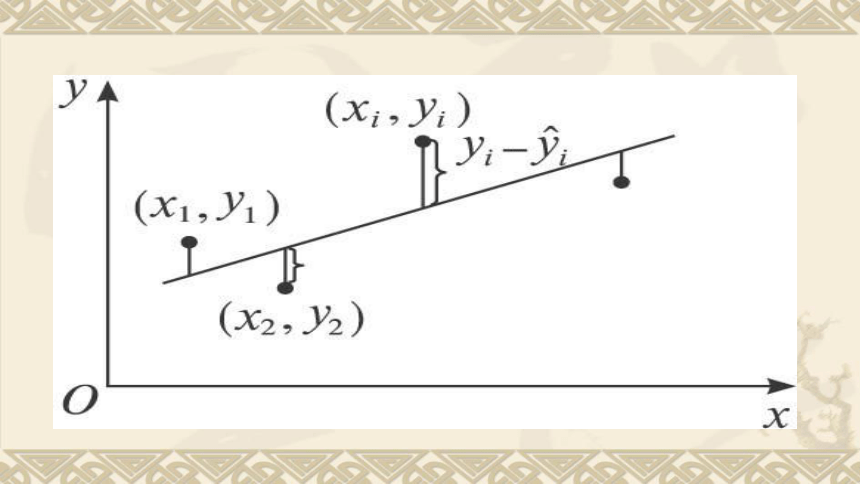
(2)你能从散点图中发现温度与饮料杯数近似成什么关系吗? 由图可见,所有数据的点都分布在一条直线附近,显然这样的直线还可以画出许多条,而我们希望找出其中的一条,它能最好地反映x与Y之间的关系。我们要找出一条直线,使这条直线“最贴近”已知的数据点。记此直线方程是上式叫做Y对于x的回归直线方程,
b叫做回归系数。最小二乘法: 用最小二乘法求回归直线方程中a,b有下面的公式:其中(1)列表
(2)计算平均数
(3)计算xi与yi的积,求 和
(4)计算xi2 ,求和
(5)将上述有关结果代入公式求回归直线方程的步骤 (3)用所求回归方程预测该地区2017年的人民币储蓄存款.注意:通过散点图判断两个变量具有线性相关关系后,再求出回归方程进行估计和预测.否则,若两个变量不具备相关关系或它们之间的相关关系不显著,即使求出回归方程也毫无意义练习2:公安人员在破案时常常根据现场作案人留下的脚印来推断犯人的身高,
人的脚印(x厘米)与身高(y厘米)成线性相关关系,回归方程近似为y=7x-3.07
(1)若某犯人的脚印为24.5厘米,则该犯人的身高大约为多少(保留整数)
(2)在一次案件中抓获了两个嫌疑人,一个身高180厘米,一个身高为175厘米,而现场测量的脚印为26.3厘米,请你推断一下两个人谁的作案可能性更大3.某数学老师身高176cm,他爷爷、父亲和儿子的身高分别是173cm,170cm和182cm.因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测他孙子的身高为___ 170176182 6.设有一个回归方程y=2-1.5x,则变量x增加1个单位时( )
A.y平均增加1.5个单位B.y平均增加2个单位
C.y平均减少1.5个单位D.y平均减少2个单位小结1.了解最小二乘法原理
2.能根据给出的回归方程系数公式建立线性回归方程
作业:教材79页练习A组,B组3.具有线性相关关系的两个变量求得的回归方程才有意义(用散点图判断)
课题:两个变量的线性相关
高一年级
人教B版必修3
))图3图4例1:下表是某小卖部6天卖出热茶的杯数与当天气温的对比表: (1)将上表中的数据制成散点图.
(2)你能从散点图中发现温度与饮料杯数近似成什么关系吗? 由图可见,所有数据的点都分布在一条直线附近,显然这样的直线还可以画出许多条,而我们希望找出其中的一条,它能最好地反映x与Y之间的关系。我们要找出一条直线,使这条直线“最贴近”已知的数据点。记此直线方程是上式叫做Y对于x的回归直线方程,
b叫做回归系数。最小二乘法: 用最小二乘法求回归直线方程中a,b有下面的公式:其中(1)列表
(2)计算平均数
(3)计算xi与yi的积,求 和
(4)计算xi2 ,求和
(5)将上述有关结果代入公式求回归直线方程的步骤 (3)用所求回归方程预测该地区2017年的人民币储蓄存款.注意:通过散点图判断两个变量具有线性相关关系后,再求出回归方程进行估计和预测.否则,若两个变量不具备相关关系或它们之间的相关关系不显著,即使求出回归方程也毫无意义练习2:公安人员在破案时常常根据现场作案人留下的脚印来推断犯人的身高,
人的脚印(x厘米)与身高(y厘米)成线性相关关系,回归方程近似为y=7x-3.07
(1)若某犯人的脚印为24.5厘米,则该犯人的身高大约为多少(保留整数)
(2)在一次案件中抓获了两个嫌疑人,一个身高180厘米,一个身高为175厘米,而现场测量的脚印为26.3厘米,请你推断一下两个人谁的作案可能性更大3.某数学老师身高176cm,他爷爷、父亲和儿子的身高分别是173cm,170cm和182cm.因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测他孙子的身高为___ 170176182 6.设有一个回归方程y=2-1.5x,则变量x增加1个单位时( )
A.y平均增加1.5个单位B.y平均增加2个单位
C.y平均减少1.5个单位D.y平均减少2个单位小结1.了解最小二乘法原理
2.能根据给出的回归方程系数公式建立线性回归方程
作业:教材79页练习A组,B组3.具有线性相关关系的两个变量求得的回归方程才有意义(用散点图判断)
