3.3.1 几何概型 课件(19张PPT)
文档属性
| 名称 | 3.3.1 几何概型 课件(19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 9.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-23 00:00:00 | ||
图片预览





文档简介
课件19张PPT。复习:1古典概型(1)所有可能出现的基本事件只有有限个(有限性)(2)每个基本事件出现的可能性相等(等可能性)
我们将具有这两个特点概率模型称为古典概率模型2古典概型的概率公式P(A)=A包含基本事件的个数基本事件的总数复习题:在0到10中,任意取出一个整数,
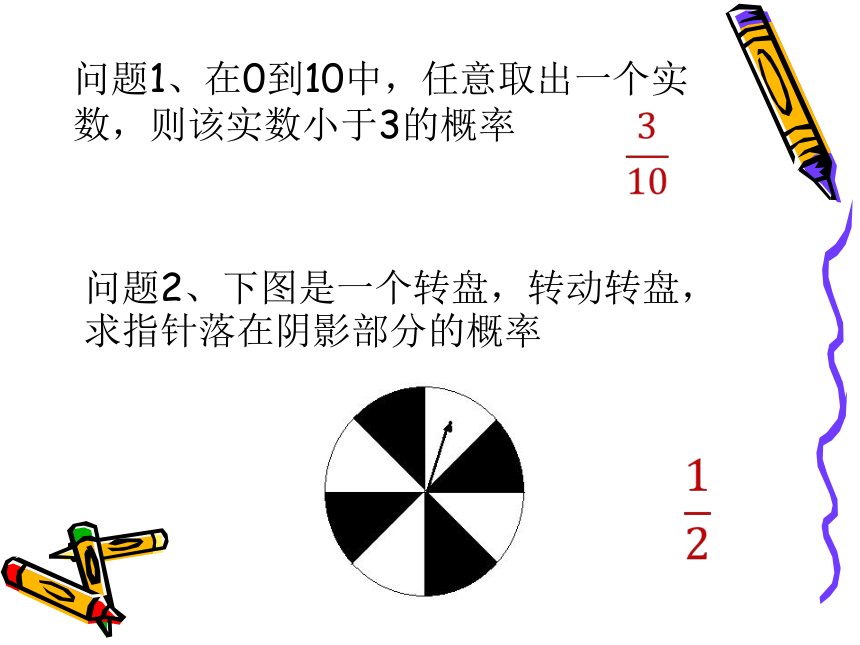
则该整数小于3的概率3.3.1几何概型问题1、在0到10中,任意取出一个实数,则该实数小于3的概率?问题2、下图是一个转盘,转动转盘,求指针落在阴影部分的概率?定义:如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称几何概型
特征:(1)无限性:基本事件个数无限
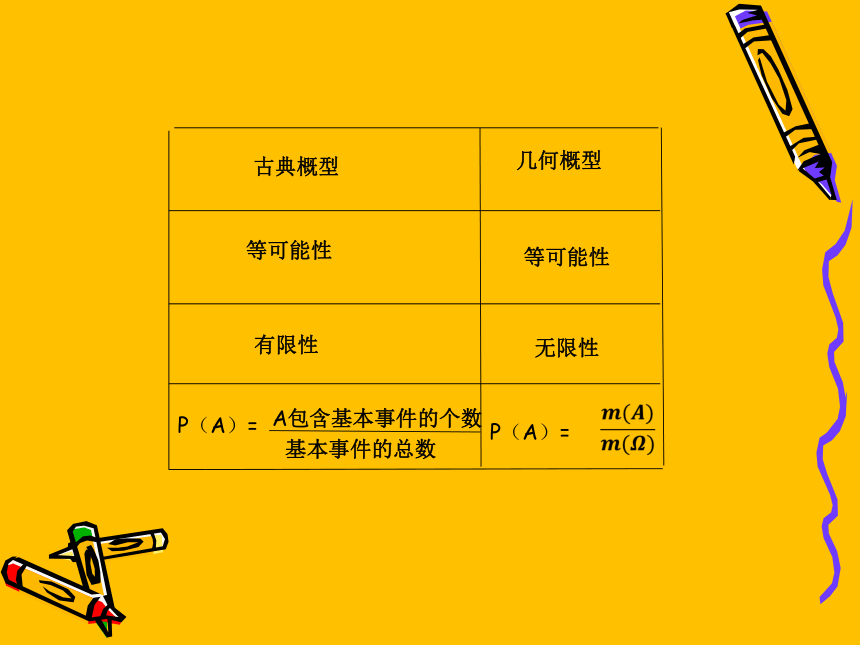
(2)等可能性:基本事件出现的可能性相同古典概型几何概型等可能性等可能性有限性无限性判断以下各题的是何种概率模型,并求相应概率
(1)在集合 A= {0,1,2,3,4,5,6,7,8,9} 中任取一个元素a,则a≤3的概率为
(2)已知点O(0,0),点M(10,0),在线段OM上任取一
点P ,则∣PM∣≥7的概率为 口答:(1)为古典概率模型, P(a≤3)=(2)为几何概型,则∣PM∣≥7的概率为
??1.长度问题:取一根长度为3m的绳子,拉直后在任意位置剪断,那么剪得两段的长度都不小于1m的概率有多大取一根长度为3m的绳子,拉直后在任意位置剪断,那么剪得两段的长度都不小于1m的概率有多大?基础训练:故由几何概型的知识可知,事件A发生的概率为:3m1m1m设 “剪得两段绳长都不小于1m”为事件A则把线段三等分,当剪断中间一段时,事件A发生故由几何概型的知识可知,事件A发生的概率为:解:由题意可得是与长度有关的几何概型问题 2.面积问题:如右下图所示的单位圆,假设你在每个图形上随机掷一枚飞镖,分别计算它落到阴影部分的概率.解:由题意可得?故几何概型的知识可知,事件A、B发生的概率分别为:设 “飞镖落在第一个图形的阴影部分”为事件A,
“飞镖落在第二个图形的阴影部分”为事件B。?3.体积问题:有一杯1升的水,其中含有1个细菌,用一个小杯从这杯水中取出0.1升,求小杯水中含有这个细菌的概率.?3. 在1000mL的水中有一个草履虫,现从中任取出2mL水样放到显微镜下观察,发现草履虫的概率. 0.0022 在1万平方千米的海域中有40平方千米的大陆架储藏着石油,如果在海域中任意点钻探,钻到油层面的概率 .0.0041.在区间(0,10)内的所有实数中随机取一个实数a,
则这个实数a>7的概率为 .
0.3当堂检测:题组一:与长度有关的几何概型当你到一个红绿灯路口时,红灯的时间为30秒,黄灯的时间为5秒,绿灯的时间为45秒,你看到黄灯的概率是多少
_______
.?题组二:与体积有关的几何概型已知棱长为2的正方体,内切球O,若在正方体内任取一点,则这一点不在球内的概率为
_______.?题组三:与角度有关的几何概型变式:在等腰直角△ABC中,在斜边AB上任取一点M,求AM小于AC的概率.在等腰直角△ABC中,过直角顶点C任作一条射线L与斜边AB交于点M,求AM小于AC的概率.??课堂小结1.几何概型的特征:无限性、等可能性
2.几何概型主要用于解决与测度有关的题目
3.注意理解几何概型与古典概型的区别,背景相似的问题,当等可能的角度不同时,其概率是不一样的
4.如何将实际问题转化为几何概型的问题,利用几何概型公式求解。数学来源于生活,应用于生活
谢谢!
我们将具有这两个特点概率模型称为古典概率模型2古典概型的概率公式P(A)=A包含基本事件的个数基本事件的总数复习题:在0到10中,任意取出一个整数,
则该整数小于3的概率3.3.1几何概型问题1、在0到10中,任意取出一个实数,则该实数小于3的概率?问题2、下图是一个转盘,转动转盘,求指针落在阴影部分的概率?定义:如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称几何概型
特征:(1)无限性:基本事件个数无限
(2)等可能性:基本事件出现的可能性相同古典概型几何概型等可能性等可能性有限性无限性判断以下各题的是何种概率模型,并求相应概率
(1)在集合 A= {0,1,2,3,4,5,6,7,8,9} 中任取一个元素a,则a≤3的概率为
(2)已知点O(0,0),点M(10,0),在线段OM上任取一
点P ,则∣PM∣≥7的概率为 口答:(1)为古典概率模型, P(a≤3)=(2)为几何概型,则∣PM∣≥7的概率为
??1.长度问题:取一根长度为3m的绳子,拉直后在任意位置剪断,那么剪得两段的长度都不小于1m的概率有多大取一根长度为3m的绳子,拉直后在任意位置剪断,那么剪得两段的长度都不小于1m的概率有多大?基础训练:故由几何概型的知识可知,事件A发生的概率为:3m1m1m设 “剪得两段绳长都不小于1m”为事件A则把线段三等分,当剪断中间一段时,事件A发生故由几何概型的知识可知,事件A发生的概率为:解:由题意可得是与长度有关的几何概型问题 2.面积问题:如右下图所示的单位圆,假设你在每个图形上随机掷一枚飞镖,分别计算它落到阴影部分的概率.解:由题意可得?故几何概型的知识可知,事件A、B发生的概率分别为:设 “飞镖落在第一个图形的阴影部分”为事件A,
“飞镖落在第二个图形的阴影部分”为事件B。?3.体积问题:有一杯1升的水,其中含有1个细菌,用一个小杯从这杯水中取出0.1升,求小杯水中含有这个细菌的概率.?3. 在1000mL的水中有一个草履虫,现从中任取出2mL水样放到显微镜下观察,发现草履虫的概率. 0.0022 在1万平方千米的海域中有40平方千米的大陆架储藏着石油,如果在海域中任意点钻探,钻到油层面的概率 .0.0041.在区间(0,10)内的所有实数中随机取一个实数a,
则这个实数a>7的概率为 .
0.3当堂检测:题组一:与长度有关的几何概型当你到一个红绿灯路口时,红灯的时间为30秒,黄灯的时间为5秒,绿灯的时间为45秒,你看到黄灯的概率是多少
_______
.?题组二:与体积有关的几何概型已知棱长为2的正方体,内切球O,若在正方体内任取一点,则这一点不在球内的概率为
_______.?题组三:与角度有关的几何概型变式:在等腰直角△ABC中,在斜边AB上任取一点M,求AM小于AC的概率.在等腰直角△ABC中,过直角顶点C任作一条射线L与斜边AB交于点M,求AM小于AC的概率.??课堂小结1.几何概型的特征:无限性、等可能性
2.几何概型主要用于解决与测度有关的题目
3.注意理解几何概型与古典概型的区别,背景相似的问题,当等可能的角度不同时,其概率是不一样的
4.如何将实际问题转化为几何概型的问题,利用几何概型公式求解。数学来源于生活,应用于生活
谢谢!
