3.4 概率的应用 课件(32张PPT)
文档属性
| 名称 | 3.4 概率的应用 课件(32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 858.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-23 09:11:25 | ||
图片预览










文档简介
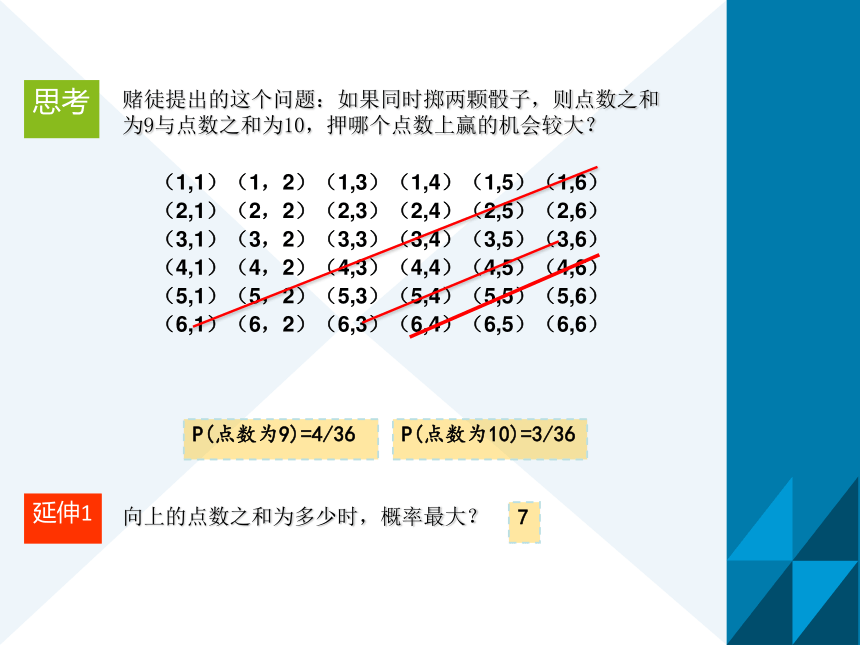
课件32张PPT。3.4 概率的应用情境导入:如何设计一个方案,在不用捞出池塘内所有的鱼的前提下,估计池塘中鱼的总数?方案1:为了估计水库中的鱼的尾数,先从水库中捕出2000尾鱼,给每尾鱼作上记号,不影响其存活,然后放回水库。经过适当的时间,让其和水库中其余的鱼充分混合,再从水库中捕出500尾鱼,查看其中有记号的鱼,发现有40尾。试根据上述数据,估计水库内鱼的尾数。解:设水库中鱼的尾数为n,从水库中任捕一尾,做记号的鱼出现的概率约为 ,第二次从水库中捕出500尾,带有记号的鱼有40尾,则带记号的鱼出现的频率(代替概率)为 则解得n≈25000.所以水库中约有鱼25000尾 .变式 假设开始捕出M条鱼并做上记号,充分混合后,捕出N条,发现带记号的有n条,则估计鱼库中大约有鱼多少条?50%100%75%25%60%卡尔达诺思考赌徒提出的这个问题:如果同时掷两颗骰子,则点数之和为9与点数之和为10,押哪个点数上赢的机会较大?(1,1)(1,2)(1,3)(1,4)(1,5)(1,6)
(2,1)(2,2)(2,3)(2,4)(2,5)(2,6)
(3,1)(3,2)(3,3)(3,4)(3,5)(3,6)
(4,1)(4,2)(4,3)(4,4)(4,5)(4,6)
(5,1)(5,2)(5,3)(5,4)(5,5)(5,6)
(6,1)(6,2)(6,3)(6,4)(6,5)(6,6)P(点数为9)=4/36P(点数为10)=3/36向上的点数之和为多少时,概率最大?延伸17(1,1)(1,2)(1,3)(1,4)(1,5)(1,6)
(2,1)(2,2)(2,3)(2,4)(2,5)(2,6)
(3,1)(3,2)(3,3)(3,4)(3,5)(3,6)
(4,1)(4,2)(4,3)(4,4)(4,5)(4,6)
(5,1)(5,2)(5,3)(5,4)(5,5)(5,6)
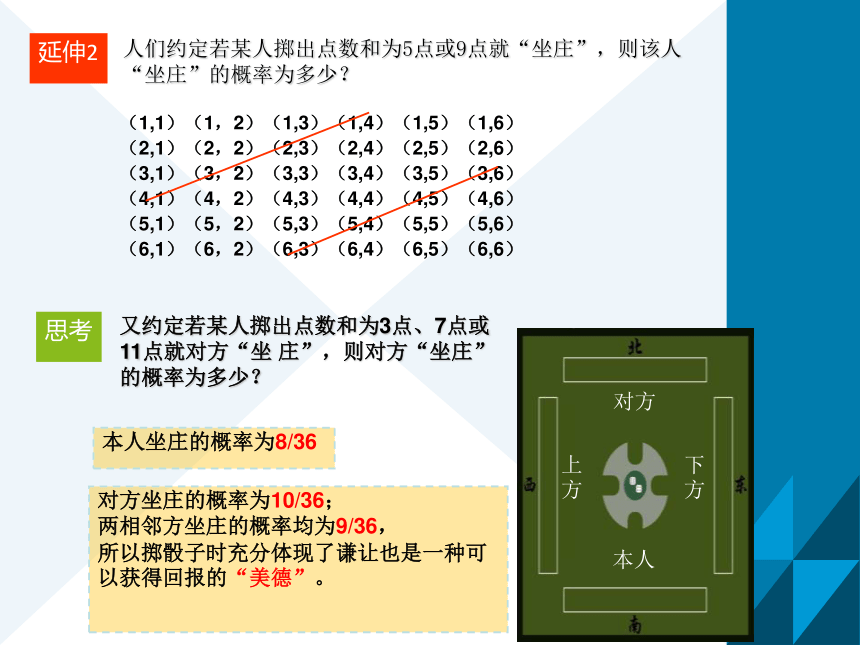
(6,1)(6,2)(6,3)(6,4)(6,5)(6,6)人们约定若某人掷出点数和为5点或9点就“坐庄”,则该人“坐庄”的概率为多少?延伸2本人坐庄的概率为8/36
又约定若某人掷出点数和为3点、7点或11点就对方“坐 庄”,则对方“坐庄”的概率为多少?对方坐庄的概率为10/36;
两相邻方坐庄的概率均为9/36,
所以掷骰子时充分体现了谦让也是一种可以获得回报的“美德”。思考1、有限性:一次试验中只有有限个基本事件2、等可能性:每个基本事件发生的可能性是相等的 古典概型的特征 古典概型的概率 若某个随机事件A 包含n 个基本 事件,则事件A 发生的概率 即几何概型的含义是什么?它有哪两个基本特点?含义:每个事件发生的概率只与构成该事件区域的
长度(面积或体积)成比例的概率模型.
特点:(1)可能出现的结果有无限多个;
(2)每个结果发生的可能性相等.
在几何概型中,事件A发生的概率计算公式是什么?课前预习问题2 举例说明你发现生活中有哪些地方用到了概率的知识?问题3 观察键盘上各个键盘的大小及位置,你发现空格键最大,而且位置最便于使用,而Q,Z键的位置相对较为偏僻,这是偶然的吗?为什么这样设计?例1. 在英语中某些字母出现的概率远远高于另外一些字母.在进行了更深入的研究之后,人们还发现各个字母被使用的频率相当稳定.例如,下面就是英文字母使用频率的一份统计表.一、在程序设计方面的应用 从表中我们可以看出,空格的使用频率最高.有鉴于此,人们在设计键盘时,空格键不仅最大,而且放在使用方便的位置. 问题3 在使用汉字输入法时,当我们输入拼音后,则提示几种可供选择的词条。 这些词条是随机给出的吗?研究这些词条出现的顺序,你有什么发现? 近年来对汉语的统计研究有了很大的发展.关于汉字的使用频率已有初步统计资料,对汉语常用词也作了一些统计研究.这些信息对汉字输入方案等的研制有很大帮助.同类应用---汉语系统 如图,当输入拼音“shu”,则提示有以下几种可供选择:1.数,2.书,3.树,4.属,5.署……这个显示顺序基本上就是按照拼音为“shu”的汉字出现频率从大到小排列的. 例2 在密码的编制和破译中,外交官和将军们关心的问题是如何使盟友容易译出电文而敌人不能破译.
为了保密,通讯双方事先有一个秘密
约定,称为密钥.发送信息方要把发出的真
实信息——明文,按密钥规定,变成密文.
接收方将密文按密钥还原成明文. 二、在密码技术方面的应用 古罗马伟大的军事和政治家凯撒大帝把
明文中的每个字母按次序后移三位之后的字
母来代替,形成密文.接收方收到密文后,将
每个字母前移三位后便得到明文.
这是一种原始的编制密码方法。 问题4 这种方法使用了很长一段时间后,有人掌握了破译的方法。你知道是如何破译的吗? 研究各个字母被使用的频率 现代保密系统采用了能确保每个字母出现在密文中的概率都相等的技术. 一种理论上不可破译的密码是“一次性密码本”(用后立即销毁). 这种密码本是一长串的随机数,每个都在1和26之间.这样一种密码本可能从以下数开始:19,7,12,1,3,8,…. 。 如“ELEVEN”这个词,用按字母表顺序排在E后面第19个字母表示E,而用L后面第7个字母表示L,等等.因此,ELEVEN变成了XSQWHV. 注意,尽管在明文中“E”出现3次,但是在密文XSQWHV中却是用三个不同的字母来替换的. 1、大学生中看过不健康书籍的人数的
百分比
2、某群体中服用过兴奋剂的比例数
3、大学生考试作弊所占的比例数
4、市民乘坐公共汽车逃票的百分数
5、一群人中参加赌博、吸毒的比例数
6、个体经营者偷税漏税的比例数三、在社会调查方面的应用 社会调查人员希望从人群的随机抽样调查中得到对他们所提问题诚实的回答.但是被采访者常常不愿意如实地作出应答.如要调查问题7 如果让你做这种调查,你能否想个办法,让被采访者消除这种不情愿情绪,做出诚实的回答? 1965年Stanley L. Warner发明了一种应用概率知识来消除这种不愿意情绪的方法. Warner的随机化应答方法要求人们随机地回答所提两个问题中的一个,而不必告诉采访者回答的是哪个问题. 两个问题中有一个是敏感的或者是令人为难的;另一个问题是无关紧要的. 这样应答者将乐意如实地回答问题,因为只有他知道自己回答的是哪个问题. 例2 在调查运动员服用兴奋剂的时候,无关紧要的问题是“你的身份证号码的尾数是奇数吗”,敏感的问题是“你服用过兴奋剂吗”,然后要求被调查的运动员掷一枚硬币.如果出现正面,就回答第一个问题,否则回答第二个问题. 假如我们把这种方法用于200个被调查的运动员,得到54个“是”的回答.你能估计这群人中大约有百分之多少的人服用过兴奋剂吗?变式练习 如果调查300名运动员中,共有85人回答“ 是”,你能估计出人群中服用兴奋剂的百分比吗?三、在社会调查方面的应用例3. 在42位美国总统中,有两人的生日相同,三人卒日相同。什尔克生于1795年11月2日,哈定则生于1865年11月2日;门罗卒于1831年7月4日,而亚当斯、杰佛逊都卒于1826年7月4日。还有两位总统的死期都是3月8日:费尔莫死于1874年,塔夫脱死于1930年,这是巧合吗? 解:这是历史上有名的生日问题,记n为相关的人数,n个人中至少有两人的生日在同一天的概率为P(A),则有下表: 上表所列的答案足以引起多数人的惊奇,因为“至少有两人生日相同”这件事情发生的概率,并不是大多数人直觉想象中的那样小,而是相当大, 由表中可以看出,当人数是40时,“至少有两人生日相同”的概率为0.89,因此,在41位美国总统中,有两人生日相同,三人卒日相同,根本不是什么巧合,而是很正常的.例3.深夜,一辆出租车被牵涉进一起交通事故,该市有两家出租车公司:红色出租车公司和蓝色出租车公司,其中蓝色出租车公司和红色出租车公司分别占整个城市出租车的85%和15%,据现场目击证人说,事故现场的出租车是红色的,对证人的辨别能力作了测试,测得他辨认颜色的正确率为80%,于是警察就认定红色出租车具有较大的肇事嫌疑。 请问警察的认定对红色出租车公平吗?试说明理由。 解:设该城市有出租车1000辆,那么依题意可得如下信息:从表中可以看出,当证人说出租车是红色时,且经确认是红色的概率为 而是蓝色的概率为 在这种情况下,以证人的证词作为推断的依据,对红色出租车显然是不公平的。4.在一个实验中,一种血清被注射到500只豚鼠体内,最初,这些豚鼠中150只有圆形细胞,250只有椭圆形细胞,100只有不规则形状细胞,被注射这种血清之后,没有一个具有圆形细胞的豚鼠被感染,50个具有椭圆形细胞的豚鼠被感染,具有不规则形状细胞的豚鼠全部被感染。根据实验结果,估计具有下列细胞有豚鼠被这种血清感染的概率:
(1)圆形细胞;(2)椭圆形细胞;(3)不规则形状细胞。课堂检测 为了了解学生遵守《中华人民共和国交通安全法》情况,调查部门在某学校进行了如下的随机调查:向被调查者提出两个问题:①你的学号是奇数吗?②在过路口时你是否闯过红灯?要求被调查者背对调查人员掷一枚硬币,如果出现正面,就回答第①个问题,否则回答第②个问题.被调查者不必告诉调查人员自己回答的是哪一个问题,只需回答“是”或“不是”,因为只有被调查者本人知道自己回答了哪个问题,所以都如实作了回答.结果被调查的600人中有180人回答了“是”.由此估计在这600人中闯过红灯的人数大约为( )
A.30 B.60 C.120 D.150?12道选择题,随机选择答案做全对的概率1/16777216,请大家努力学习,不要把希望寄托在虚无缥缈的运气上.在9班:“周一、安明珠、赵艺凡、孙霏”四位同学组成一个学习小组的概率为1/5006386,请同学们珍惜小组同学之间的缘份和友谊!买一注双色球彩票中一等奖的概率为1/17721088,请你用平常心购买福利彩票,多为福彩事业做一份贡献.长期赌博输的概率为1(必然事件),因为钱都被赌场赚走了!请告诫自己和亲朋好友远离赌博!课堂小结知识方面思想方法方面2.几何概率的计算公式1.古典概率计算公式必然与偶然思想
列举法
间接法3 概率的主要应用:程序设计,密码技术,社会调查等谢 谢
(2,1)(2,2)(2,3)(2,4)(2,5)(2,6)
(3,1)(3,2)(3,3)(3,4)(3,5)(3,6)
(4,1)(4,2)(4,3)(4,4)(4,5)(4,6)
(5,1)(5,2)(5,3)(5,4)(5,5)(5,6)
(6,1)(6,2)(6,3)(6,4)(6,5)(6,6)P(点数为9)=4/36P(点数为10)=3/36向上的点数之和为多少时,概率最大?延伸17(1,1)(1,2)(1,3)(1,4)(1,5)(1,6)
(2,1)(2,2)(2,3)(2,4)(2,5)(2,6)
(3,1)(3,2)(3,3)(3,4)(3,5)(3,6)
(4,1)(4,2)(4,3)(4,4)(4,5)(4,6)
(5,1)(5,2)(5,3)(5,4)(5,5)(5,6)
(6,1)(6,2)(6,3)(6,4)(6,5)(6,6)人们约定若某人掷出点数和为5点或9点就“坐庄”,则该人“坐庄”的概率为多少?延伸2本人坐庄的概率为8/36
又约定若某人掷出点数和为3点、7点或11点就对方“坐 庄”,则对方“坐庄”的概率为多少?对方坐庄的概率为10/36;
两相邻方坐庄的概率均为9/36,
所以掷骰子时充分体现了谦让也是一种可以获得回报的“美德”。思考1、有限性:一次试验中只有有限个基本事件2、等可能性:每个基本事件发生的可能性是相等的 古典概型的特征 古典概型的概率 若某个随机事件A 包含n 个基本 事件,则事件A 发生的概率 即几何概型的含义是什么?它有哪两个基本特点?含义:每个事件发生的概率只与构成该事件区域的
长度(面积或体积)成比例的概率模型.
特点:(1)可能出现的结果有无限多个;
(2)每个结果发生的可能性相等.
在几何概型中,事件A发生的概率计算公式是什么?课前预习问题2 举例说明你发现生活中有哪些地方用到了概率的知识?问题3 观察键盘上各个键盘的大小及位置,你发现空格键最大,而且位置最便于使用,而Q,Z键的位置相对较为偏僻,这是偶然的吗?为什么这样设计?例1. 在英语中某些字母出现的概率远远高于另外一些字母.在进行了更深入的研究之后,人们还发现各个字母被使用的频率相当稳定.例如,下面就是英文字母使用频率的一份统计表.一、在程序设计方面的应用 从表中我们可以看出,空格的使用频率最高.有鉴于此,人们在设计键盘时,空格键不仅最大,而且放在使用方便的位置. 问题3 在使用汉字输入法时,当我们输入拼音后,则提示几种可供选择的词条。 这些词条是随机给出的吗?研究这些词条出现的顺序,你有什么发现? 近年来对汉语的统计研究有了很大的发展.关于汉字的使用频率已有初步统计资料,对汉语常用词也作了一些统计研究.这些信息对汉字输入方案等的研制有很大帮助.同类应用---汉语系统 如图,当输入拼音“shu”,则提示有以下几种可供选择:1.数,2.书,3.树,4.属,5.署……这个显示顺序基本上就是按照拼音为“shu”的汉字出现频率从大到小排列的. 例2 在密码的编制和破译中,外交官和将军们关心的问题是如何使盟友容易译出电文而敌人不能破译.
为了保密,通讯双方事先有一个秘密
约定,称为密钥.发送信息方要把发出的真
实信息——明文,按密钥规定,变成密文.
接收方将密文按密钥还原成明文. 二、在密码技术方面的应用 古罗马伟大的军事和政治家凯撒大帝把
明文中的每个字母按次序后移三位之后的字
母来代替,形成密文.接收方收到密文后,将
每个字母前移三位后便得到明文.
这是一种原始的编制密码方法。 问题4 这种方法使用了很长一段时间后,有人掌握了破译的方法。你知道是如何破译的吗? 研究各个字母被使用的频率 现代保密系统采用了能确保每个字母出现在密文中的概率都相等的技术. 一种理论上不可破译的密码是“一次性密码本”(用后立即销毁). 这种密码本是一长串的随机数,每个都在1和26之间.这样一种密码本可能从以下数开始:19,7,12,1,3,8,…. 。 如“ELEVEN”这个词,用按字母表顺序排在E后面第19个字母表示E,而用L后面第7个字母表示L,等等.因此,ELEVEN变成了XSQWHV. 注意,尽管在明文中“E”出现3次,但是在密文XSQWHV中却是用三个不同的字母来替换的. 1、大学生中看过不健康书籍的人数的
百分比
2、某群体中服用过兴奋剂的比例数
3、大学生考试作弊所占的比例数
4、市民乘坐公共汽车逃票的百分数
5、一群人中参加赌博、吸毒的比例数
6、个体经营者偷税漏税的比例数三、在社会调查方面的应用 社会调查人员希望从人群的随机抽样调查中得到对他们所提问题诚实的回答.但是被采访者常常不愿意如实地作出应答.如要调查问题7 如果让你做这种调查,你能否想个办法,让被采访者消除这种不情愿情绪,做出诚实的回答? 1965年Stanley L. Warner发明了一种应用概率知识来消除这种不愿意情绪的方法. Warner的随机化应答方法要求人们随机地回答所提两个问题中的一个,而不必告诉采访者回答的是哪个问题. 两个问题中有一个是敏感的或者是令人为难的;另一个问题是无关紧要的. 这样应答者将乐意如实地回答问题,因为只有他知道自己回答的是哪个问题. 例2 在调查运动员服用兴奋剂的时候,无关紧要的问题是“你的身份证号码的尾数是奇数吗”,敏感的问题是“你服用过兴奋剂吗”,然后要求被调查的运动员掷一枚硬币.如果出现正面,就回答第一个问题,否则回答第二个问题. 假如我们把这种方法用于200个被调查的运动员,得到54个“是”的回答.你能估计这群人中大约有百分之多少的人服用过兴奋剂吗?变式练习 如果调查300名运动员中,共有85人回答“ 是”,你能估计出人群中服用兴奋剂的百分比吗?三、在社会调查方面的应用例3. 在42位美国总统中,有两人的生日相同,三人卒日相同。什尔克生于1795年11月2日,哈定则生于1865年11月2日;门罗卒于1831年7月4日,而亚当斯、杰佛逊都卒于1826年7月4日。还有两位总统的死期都是3月8日:费尔莫死于1874年,塔夫脱死于1930年,这是巧合吗? 解:这是历史上有名的生日问题,记n为相关的人数,n个人中至少有两人的生日在同一天的概率为P(A),则有下表: 上表所列的答案足以引起多数人的惊奇,因为“至少有两人生日相同”这件事情发生的概率,并不是大多数人直觉想象中的那样小,而是相当大, 由表中可以看出,当人数是40时,“至少有两人生日相同”的概率为0.89,因此,在41位美国总统中,有两人生日相同,三人卒日相同,根本不是什么巧合,而是很正常的.例3.深夜,一辆出租车被牵涉进一起交通事故,该市有两家出租车公司:红色出租车公司和蓝色出租车公司,其中蓝色出租车公司和红色出租车公司分别占整个城市出租车的85%和15%,据现场目击证人说,事故现场的出租车是红色的,对证人的辨别能力作了测试,测得他辨认颜色的正确率为80%,于是警察就认定红色出租车具有较大的肇事嫌疑。 请问警察的认定对红色出租车公平吗?试说明理由。 解:设该城市有出租车1000辆,那么依题意可得如下信息:从表中可以看出,当证人说出租车是红色时,且经确认是红色的概率为 而是蓝色的概率为 在这种情况下,以证人的证词作为推断的依据,对红色出租车显然是不公平的。4.在一个实验中,一种血清被注射到500只豚鼠体内,最初,这些豚鼠中150只有圆形细胞,250只有椭圆形细胞,100只有不规则形状细胞,被注射这种血清之后,没有一个具有圆形细胞的豚鼠被感染,50个具有椭圆形细胞的豚鼠被感染,具有不规则形状细胞的豚鼠全部被感染。根据实验结果,估计具有下列细胞有豚鼠被这种血清感染的概率:
(1)圆形细胞;(2)椭圆形细胞;(3)不规则形状细胞。课堂检测 为了了解学生遵守《中华人民共和国交通安全法》情况,调查部门在某学校进行了如下的随机调查:向被调查者提出两个问题:①你的学号是奇数吗?②在过路口时你是否闯过红灯?要求被调查者背对调查人员掷一枚硬币,如果出现正面,就回答第①个问题,否则回答第②个问题.被调查者不必告诉调查人员自己回答的是哪一个问题,只需回答“是”或“不是”,因为只有被调查者本人知道自己回答了哪个问题,所以都如实作了回答.结果被调查的600人中有180人回答了“是”.由此估计在这600人中闯过红灯的人数大约为( )
A.30 B.60 C.120 D.150?12道选择题,随机选择答案做全对的概率1/16777216,请大家努力学习,不要把希望寄托在虚无缥缈的运气上.在9班:“周一、安明珠、赵艺凡、孙霏”四位同学组成一个学习小组的概率为1/5006386,请同学们珍惜小组同学之间的缘份和友谊!买一注双色球彩票中一等奖的概率为1/17721088,请你用平常心购买福利彩票,多为福彩事业做一份贡献.长期赌博输的概率为1(必然事件),因为钱都被赌场赚走了!请告诫自己和亲朋好友远离赌博!课堂小结知识方面思想方法方面2.几何概率的计算公式1.古典概率计算公式必然与偶然思想
列举法
间接法3 概率的主要应用:程序设计,密码技术,社会调查等谢 谢
