1.1.1 角的概念的推广 课件(26张PPT)
文档属性
| 名称 | 1.1.1 角的概念的推广 课件(26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-23 09:10:26 | ||
图片预览





文档简介
课件26张PPT。1.1角的概念的推广人教B版必修4content1、小学是如何定义角的?2、初中时,我们还学习了角的概念,它是如何定义的呢? 知识回顾有公共端点的两条射线组成的图形
角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形。射线旋转时经过的平面部分为角的内部 。 思考在体操、跳水比赛中我们经常听到这样的术语:“转体720o”
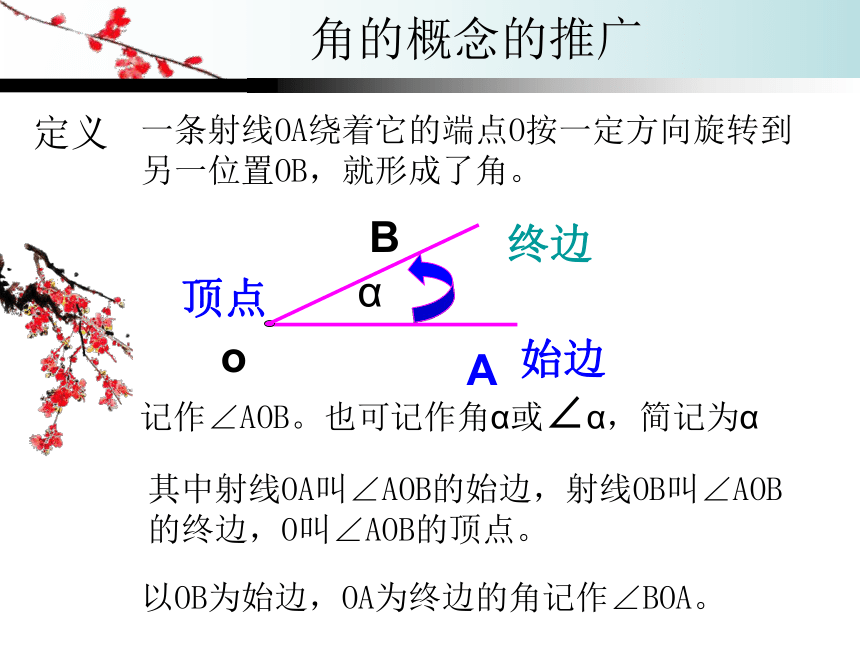
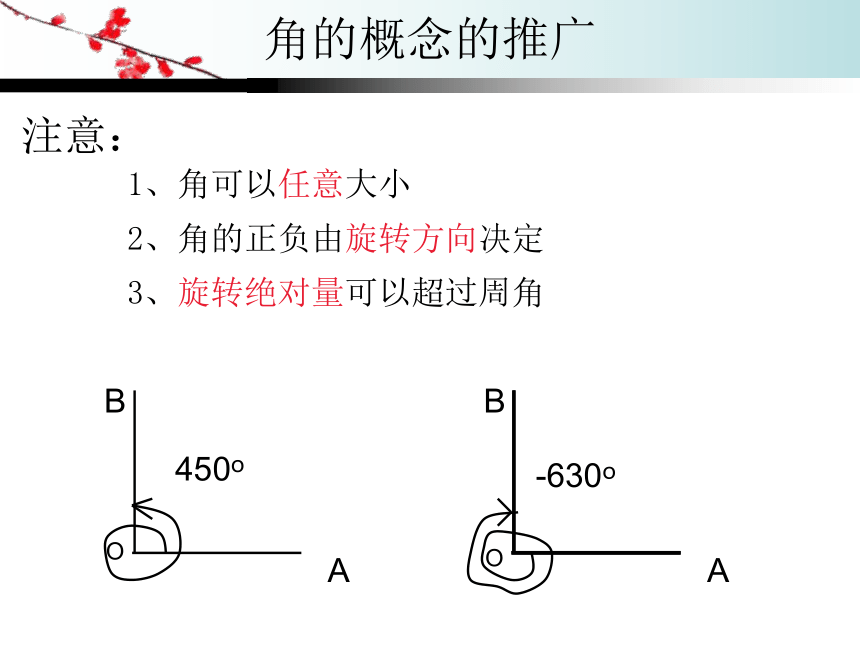
显然在生活中存在更大范围内的角,这些角超出了我们已有的认识范围。分 类正角:按逆时针方向旋转形成的角射线没有旋转,把它看成一个角按顺时针方向旋转形成的角 逆时针 顺时针规 定负角:零角:角的概念的推广一条射线OA绕着它的端点O按一定方向旋转到另一位置OB,就形成了角。定义以OB为始边,OA为终边的角记作∠BOA。其中射线OA叫∠AOB的始边,射线OB叫∠AOB的终边,O叫∠AOB的顶点。记作∠AOB。也可记作角α或∠α,简记为α始边终边顶点角的概念的推广注意:2、角的正负由旋转方向决定1、角可以任意大小3、旋转绝对量可以超过周角450o-630o角 的 运 算
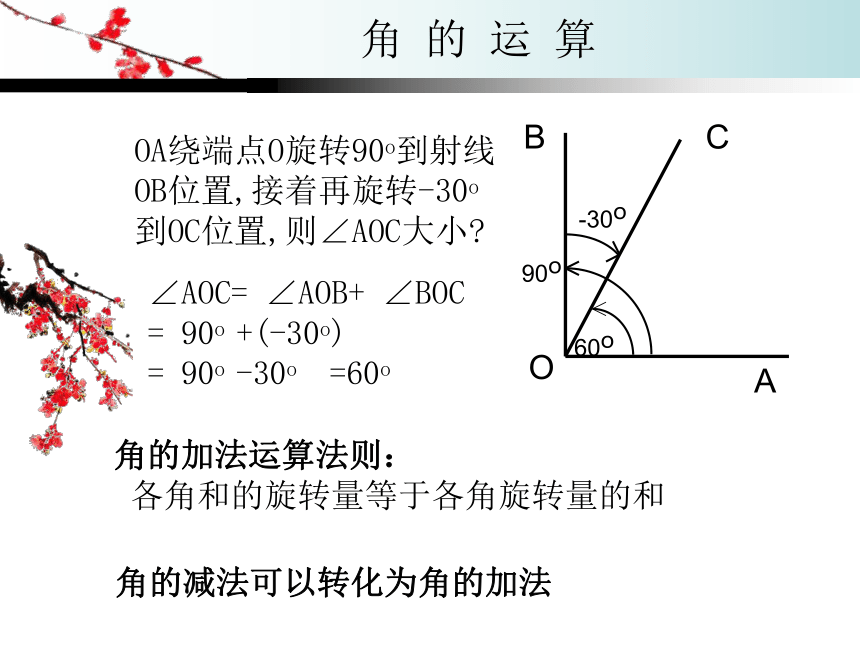
角的减法可以转化为角的加法OA绕端点O旋转90o到射线OB位置,接着再旋转-30o到OC位置,则∠AOC大小?角的加法运算法则:
各角和的旋转量等于各角旋转量的和∠AOC= ∠AOB+ ∠BOC
= 90o +(-30o)
= 90o -30o =60o例1.射线OA绕端点O顺时针旋转80o到OB位置,接着逆时针旋转250o到OC位置,然后再顺时针旋转270o到OD位置,求∠AOD大小。解:由题意知∠AOB=-80o ∠BOC=250o
∠COD=-270o因此
∠AOD=∠AOB+∠BOC+∠COD
=-80o + 250o-270o =-100o
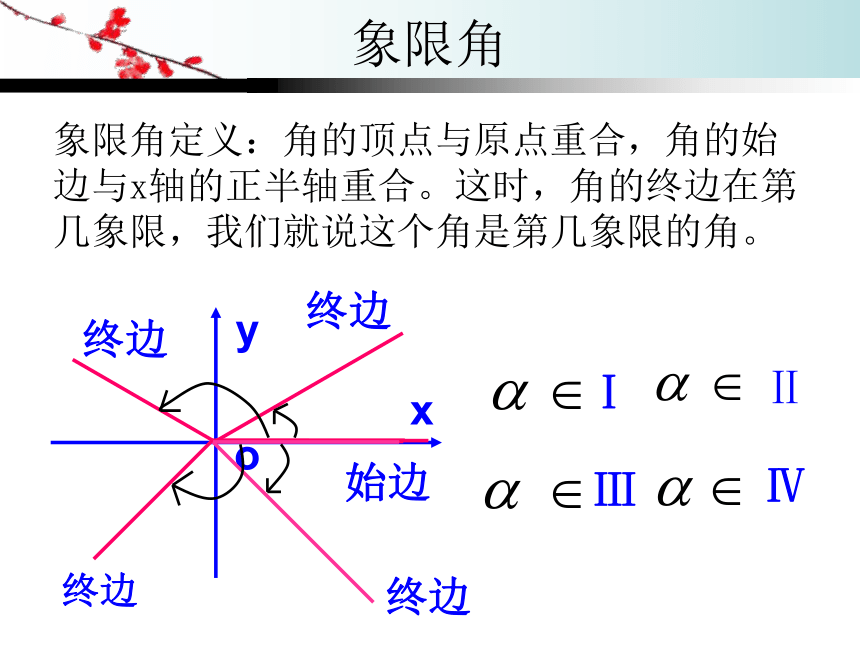
content象限角象限角定义:角的顶点与原点重合,角的始边与x轴的正半轴重合。这时,角的终边在第几象限,我们就说这个角是第几象限的角。坐标轴上的角是不是任意角都可以归结为是象限角,为什么? 如果角的终边落在了坐标轴上,就认为这个角不属于任何象限。坐标轴上的角:例如:角的终边落在X轴正半轴或Y轴负半轴上。思考看下面几个角是第几象限的角,并在坐标系中画出它们。
30o 124o 390o 210o -45o 3900content3900-33003900=300+3600-3300=300+(-3600)=300+ 1 x3600 =300+(-1)x3600 300 =300+ 0 x3600与300终边相同的角的一般形式为
300+K·3600,K ∈ Z终边相同的角与α终边相同的角
对于任意一个角α,与它终边相同的角的
集合可以表示为
S={β|β=α+k×3600,k∈Z} 注意:(1) K ∈ Z(2)α是任意角(3)K·360°与α之间是“+”号(4)终边相同的角有无数多个,它们 相差360°的整数倍巩固新知例2、在0o~360o度范围内,找出与下列各角终边相同的角,并判断它是哪个象限的角?(1)-150°(2)650 °(3) -950 °15'解(1)-150°=-360 °+210 °(2)650°=360°+290°(3)-950°15 ' = -3×360°+129°45 '所以与-150 °角终边相同的角是210°角,它是第三象限角。所以与650°角终边相同的角是290°角,它是第四象限角。 所以与-950°15 ' 角终边相同的角是129°45 ' 角,
它是第二象限角。 巩固新知例3:分别写出与下列各角终边相同的角的集合S ,
并把S中 满足不等式-3600≤ <7200的元素 写出来
(1) 600(2)363014'解(1) S={β|β=600+k×3600,k∈Z}
S中 满足不等式-3600≤ β <7200的元素600+(-1)×3600 = -3000
600+ 0 ×3600 = 600
600+ 1 ×3600 = 4200巩固新知(2)S={β|β=363014'+k×3600,k∈Z}
S中 满足不等式-3600≤ β<7200的元素
363014' + 0×3600 = 363014'
363014' + (-1)×3600 = 3014'
363014' + ( -2)×3600 =-356046'例3:分别写出与下列各角终边相同的角的集合S ,
并把S中 满足不等式-3600≤ <7200的元素 写出来
(1) 600(2)363014'巩固新知例4 写出终边落在x轴上的角的集合。终边落在x轴上的情形001800+K · 3600+K· 3600巩固新知例4 写出终边落在x轴上的角的集合。解:终边落在x轴正半轴上的角的集合为S1={β | β=00+K?3600,K∈Z} ={β| β=00+2K?1800,K∈Z}={β| β=00+1800 的偶数倍}终边落在x轴负半轴上的角的集合为S2={β| β=1800+K?3600,K∈Z}={β| β= (2K+1)?1800,K∈Z}={β| β=00+(2K+1)1800 ,K∈Z}={β| β=00+1800 的奇数倍}content巩固新知S=S1∪S2所以 终边落在x轴上的角的集合为={β|β=00+1800 的偶数倍}∪{β|β=00+1800 的奇数倍}={β| β=00+1800 的整数倍} ={β| β=00+n?1800 ,n∈Z}结论:与α终边落在同一条直线上的所有角的集合
S={β| β= α+n?1800 ,n∈Z} β=00+K?3600,K∈Zβ=900+K?3600,K∈Zβ的取值范围是00+K?3600 < β<900+K?3600,K∈Z如果β为第一象限的角,那么β的取值范围可以表示成怎样的不等式?思考与讨论课堂巩固回答下列问题2、锐角是第几象限的角?3、第一象限的角是否都是锐角?举例说明1、小于90°的角都是锐角吗?答:锐角是第一象限的角。答:第一象限的角并不都是锐角。答:小于90°的角并不都是锐角,它也有可能是零角或负角。课堂巩固判断下列语句的真、假:(1)终边相同的角一定相等;
(2)相等的角,终边一定相同;
(3)钝角不一定是第二象限角;
(4)三角形内角一定是第一、第二象限角;
(5)钟表的时针旋转而成的角是负角。课堂巩固写出终边落在y轴上的角的集合900S={β| β=900+n?1800 ,n∈Z}小结:1.任意角的概念正角负角零角1)置角的顶点于原点2)始边重合于X轴的正半轴3.象限角终边落在第几象限就是第几象限角5.与 角α终边相同的角α+K·3600,K∈Z4.坐标轴上的角6.与α终边落在同一条直线上的角α+n·1800 ,n∈Z2.角的运算作业教材第6页B组2-4题谢 谢!
角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形。射线旋转时经过的平面部分为角的内部 。 思考在体操、跳水比赛中我们经常听到这样的术语:“转体720o”
显然在生活中存在更大范围内的角,这些角超出了我们已有的认识范围。分 类正角:按逆时针方向旋转形成的角射线没有旋转,把它看成一个角按顺时针方向旋转形成的角 逆时针 顺时针规 定负角:零角:角的概念的推广一条射线OA绕着它的端点O按一定方向旋转到另一位置OB,就形成了角。定义以OB为始边,OA为终边的角记作∠BOA。其中射线OA叫∠AOB的始边,射线OB叫∠AOB的终边,O叫∠AOB的顶点。记作∠AOB。也可记作角α或∠α,简记为α始边终边顶点角的概念的推广注意:2、角的正负由旋转方向决定1、角可以任意大小3、旋转绝对量可以超过周角450o-630o角 的 运 算
角的减法可以转化为角的加法OA绕端点O旋转90o到射线OB位置,接着再旋转-30o到OC位置,则∠AOC大小?角的加法运算法则:
各角和的旋转量等于各角旋转量的和∠AOC= ∠AOB+ ∠BOC
= 90o +(-30o)
= 90o -30o =60o例1.射线OA绕端点O顺时针旋转80o到OB位置,接着逆时针旋转250o到OC位置,然后再顺时针旋转270o到OD位置,求∠AOD大小。解:由题意知∠AOB=-80o ∠BOC=250o
∠COD=-270o因此
∠AOD=∠AOB+∠BOC+∠COD
=-80o + 250o-270o =-100o
content象限角象限角定义:角的顶点与原点重合,角的始边与x轴的正半轴重合。这时,角的终边在第几象限,我们就说这个角是第几象限的角。坐标轴上的角是不是任意角都可以归结为是象限角,为什么? 如果角的终边落在了坐标轴上,就认为这个角不属于任何象限。坐标轴上的角:例如:角的终边落在X轴正半轴或Y轴负半轴上。思考看下面几个角是第几象限的角,并在坐标系中画出它们。
30o 124o 390o 210o -45o 3900content3900-33003900=300+3600-3300=300+(-3600)=300+ 1 x3600 =300+(-1)x3600 300 =300+ 0 x3600与300终边相同的角的一般形式为
300+K·3600,K ∈ Z终边相同的角与α终边相同的角
对于任意一个角α,与它终边相同的角的
集合可以表示为
S={β|β=α+k×3600,k∈Z} 注意:(1) K ∈ Z(2)α是任意角(3)K·360°与α之间是“+”号(4)终边相同的角有无数多个,它们 相差360°的整数倍巩固新知例2、在0o~360o度范围内,找出与下列各角终边相同的角,并判断它是哪个象限的角?(1)-150°(2)650 °(3) -950 °15'解(1)-150°=-360 °+210 °(2)650°=360°+290°(3)-950°15 ' = -3×360°+129°45 '所以与-150 °角终边相同的角是210°角,它是第三象限角。所以与650°角终边相同的角是290°角,它是第四象限角。 所以与-950°15 ' 角终边相同的角是129°45 ' 角,
它是第二象限角。 巩固新知例3:分别写出与下列各角终边相同的角的集合S ,
并把S中 满足不等式-3600≤ <7200的元素 写出来
(1) 600(2)363014'解(1) S={β|β=600+k×3600,k∈Z}
S中 满足不等式-3600≤ β <7200的元素600+(-1)×3600 = -3000
600+ 0 ×3600 = 600
600+ 1 ×3600 = 4200巩固新知(2)S={β|β=363014'+k×3600,k∈Z}
S中 满足不等式-3600≤ β<7200的元素
363014' + 0×3600 = 363014'
363014' + (-1)×3600 = 3014'
363014' + ( -2)×3600 =-356046'例3:分别写出与下列各角终边相同的角的集合S ,
并把S中 满足不等式-3600≤ <7200的元素 写出来
(1) 600(2)363014'巩固新知例4 写出终边落在x轴上的角的集合。终边落在x轴上的情形001800+K · 3600+K· 3600巩固新知例4 写出终边落在x轴上的角的集合。解:终边落在x轴正半轴上的角的集合为S1={β | β=00+K?3600,K∈Z} ={β| β=00+2K?1800,K∈Z}={β| β=00+1800 的偶数倍}终边落在x轴负半轴上的角的集合为S2={β| β=1800+K?3600,K∈Z}={β| β= (2K+1)?1800,K∈Z}={β| β=00+(2K+1)1800 ,K∈Z}={β| β=00+1800 的奇数倍}content巩固新知S=S1∪S2所以 终边落在x轴上的角的集合为={β|β=00+1800 的偶数倍}∪{β|β=00+1800 的奇数倍}={β| β=00+1800 的整数倍} ={β| β=00+n?1800 ,n∈Z}结论:与α终边落在同一条直线上的所有角的集合
S={β| β= α+n?1800 ,n∈Z} β=00+K?3600,K∈Zβ=900+K?3600,K∈Zβ的取值范围是00+K?3600 < β<900+K?3600,K∈Z如果β为第一象限的角,那么β的取值范围可以表示成怎样的不等式?思考与讨论课堂巩固回答下列问题2、锐角是第几象限的角?3、第一象限的角是否都是锐角?举例说明1、小于90°的角都是锐角吗?答:锐角是第一象限的角。答:第一象限的角并不都是锐角。答:小于90°的角并不都是锐角,它也有可能是零角或负角。课堂巩固判断下列语句的真、假:(1)终边相同的角一定相等;
(2)相等的角,终边一定相同;
(3)钝角不一定是第二象限角;
(4)三角形内角一定是第一、第二象限角;
(5)钟表的时针旋转而成的角是负角。课堂巩固写出终边落在y轴上的角的集合900S={β| β=900+n?1800 ,n∈Z}小结:1.任意角的概念正角负角零角1)置角的顶点于原点2)始边重合于X轴的正半轴3.象限角终边落在第几象限就是第几象限角5.与 角α终边相同的角α+K·3600,K∈Z4.坐标轴上的角6.与α终边落在同一条直线上的角α+n·1800 ,n∈Z2.角的运算作业教材第6页B组2-4题谢 谢!
