1.2.1 三角函数的定义 课件(28张PPT)
文档属性
| 名称 | 1.2.1 三角函数的定义 课件(28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 532.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-23 09:12:07 | ||
图片预览



文档简介
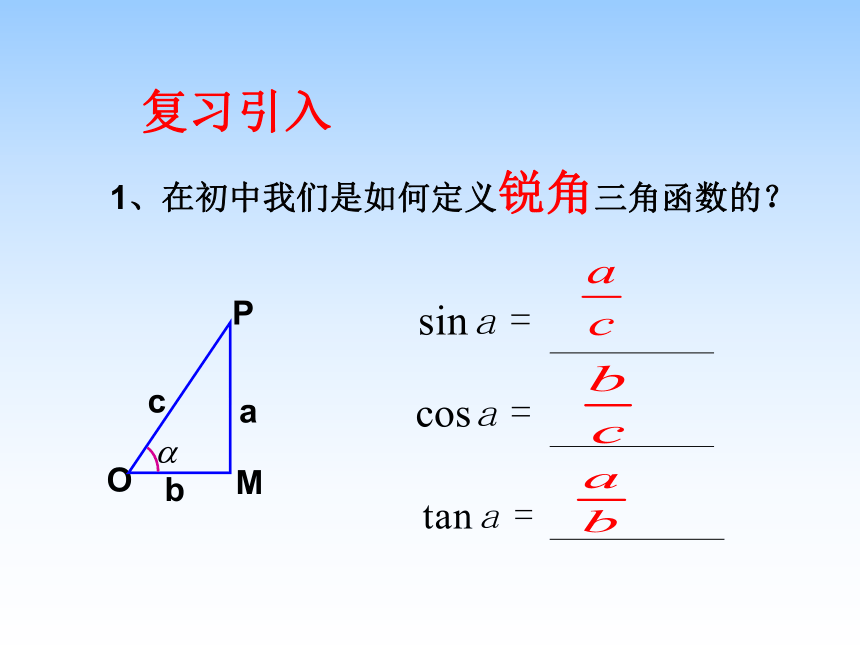
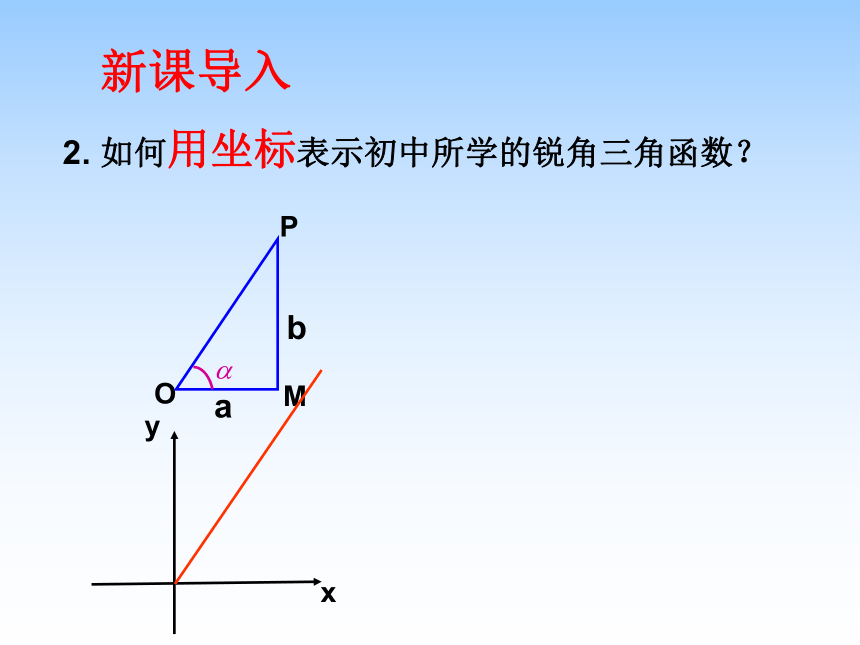
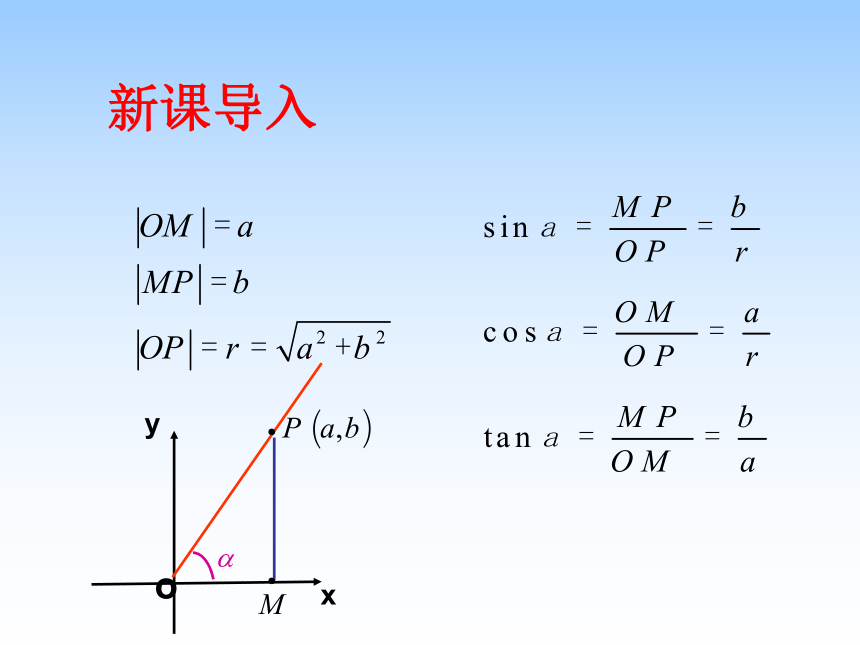
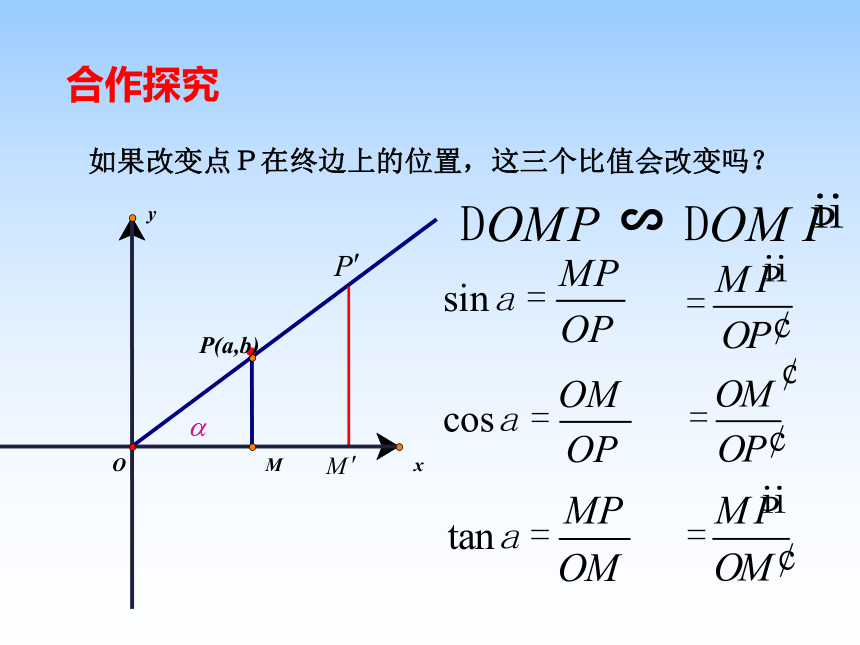
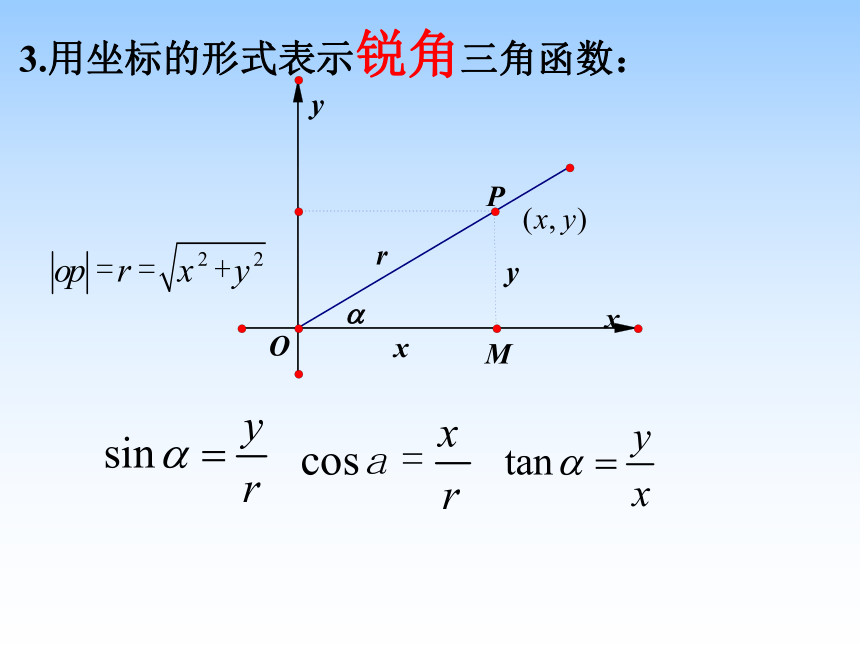
课件28张PPT。1.2.1三角函数的定义自然界的周期现象新课导入 1、在初中我们是如何定义锐角三角函数的?复习引入 2. 如何用坐标表示初中所学的锐角三角函数?新课导入 yx﹒﹒o新课导入如果改变点P在终边上的位置,这三个比值会改变吗?﹒合作探究MOyxP(a,b)∽3.用坐标的形式表示锐角三角函数: 当角度不是锐角时,而是任意角时它的三角函数又如何定义呢?概念延伸4. 任意角的三角函数 : 因为A、P在同一象限内,所以它们的坐标符号相同,因此得设OA=1,A(l,m) P(x,y)
不论点P在终边上的位置如何,它们都是定值,它们只依赖于 α 的大小,与点P在 α 终边上的位置无关,即当点P在 α终边上变化时,这三个比值始终等于定值。结论我们可以定义:角α的正弦: 角α的余弦: 角α的正切: 探究:
这样的比值能构成函数吗?
它们的自变量是什么:x、y、r还是 α ?
sinα= ,cosα= ,tanα= 正弦、余弦、正切函数都是以角为自变量,以比值为函数值的函数。(统称为三角函数)弧度制下,角的集合与实数集R之间建立了
一一对应关系三角函数可以看成以实数为自变量的函数结论:角α的其他三种函数:角α的正割: 角α的余割: 角α的余切: 三角函数的定义域例1.已知角α的终边过点P(2,-3),求α的三个三角函数值。 解:因为x=2,y=-3,所以sinα=cosα=tanα=知识应用解:(1)因为当α=0时,x=r,y=0 .所以例2. 求下列各角的三个三角函数值:
(1)0;(2)π;(3) sin0=0,cos0=1,tan0=0,(2) π;解:(2)因为当α=π时,x=-r,y=0 .所以sinπ=0,cosπ=-1,tanπ=0,(3) 解:(3)因为当α= 时,x=0,y=-r .所以sin =-1,cos =0,tan 不存在,三角函数在各象限内的符号 角α是“任意角”, 由三角函数定义可知,由于P(x, y)点的坐标x, y的正负是随角α所在的象限的变化而不同,所以三角函数的符号应由角α所在的象限确定. 探究:三角函数值在各象限的符号全为+一全正二正弦三正切四余弦三角函数值的符号:规律:例4. 确定下列三角函数值的符号:
(1)cos260o; (2)
(3)tan(-672o);(4)解: (1)260o在第三象限,所以cos260o<0.(2) - 在第四象限,所以sin(- )<0.(3) -672o在第一象限,所以tan(-672o)>0.(4) 在第四象限,所以tan( )<0.例5.设sinθ<0且tanθ>0,确定θ是第几象限的角。解:因为sinθ<0,所以θ可能是第三、四象限的角,又tanθ>0,θ可能是第一、三象限的角,综上所述,θ是第三象限的角。例6.若三角形的两内角?,?满足sin?cos?<0,则此三角形必为( )
A. 锐角三角形 B. 钝角三角形
C. 直角三角形 D. 以上三种情况都可能B你的收获1、任意角的三角函数的定义。
2、三角函数的定义域。
3、三角函数在各个象限的符号。
世上无难事,只怕有心人作业17、18页A组和B组
谢谢大家
再见
不论点P在终边上的位置如何,它们都是定值,它们只依赖于 α 的大小,与点P在 α 终边上的位置无关,即当点P在 α终边上变化时,这三个比值始终等于定值。结论我们可以定义:角α的正弦: 角α的余弦: 角α的正切: 探究:
这样的比值能构成函数吗?
它们的自变量是什么:x、y、r还是 α ?
sinα= ,cosα= ,tanα= 正弦、余弦、正切函数都是以角为自变量,以比值为函数值的函数。(统称为三角函数)弧度制下,角的集合与实数集R之间建立了
一一对应关系三角函数可以看成以实数为自变量的函数结论:角α的其他三种函数:角α的正割: 角α的余割: 角α的余切: 三角函数的定义域例1.已知角α的终边过点P(2,-3),求α的三个三角函数值。 解:因为x=2,y=-3,所以sinα=cosα=tanα=知识应用解:(1)因为当α=0时,x=r,y=0 .所以例2. 求下列各角的三个三角函数值:
(1)0;(2)π;(3) sin0=0,cos0=1,tan0=0,(2) π;解:(2)因为当α=π时,x=-r,y=0 .所以sinπ=0,cosπ=-1,tanπ=0,(3) 解:(3)因为当α= 时,x=0,y=-r .所以sin =-1,cos =0,tan 不存在,三角函数在各象限内的符号 角α是“任意角”, 由三角函数定义可知,由于P(x, y)点的坐标x, y的正负是随角α所在的象限的变化而不同,所以三角函数的符号应由角α所在的象限确定. 探究:三角函数值在各象限的符号全为+一全正二正弦三正切四余弦三角函数值的符号:规律:例4. 确定下列三角函数值的符号:
(1)cos260o; (2)
(3)tan(-672o);(4)解: (1)260o在第三象限,所以cos260o<0.(2) - 在第四象限,所以sin(- )<0.(3) -672o在第一象限,所以tan(-672o)>0.(4) 在第四象限,所以tan( )<0.例5.设sinθ<0且tanθ>0,确定θ是第几象限的角。解:因为sinθ<0,所以θ可能是第三、四象限的角,又tanθ>0,θ可能是第一、三象限的角,综上所述,θ是第三象限的角。例6.若三角形的两内角?,?满足sin?cos?<0,则此三角形必为( )
A. 锐角三角形 B. 钝角三角形
C. 直角三角形 D. 以上三种情况都可能B你的收获1、任意角的三角函数的定义。
2、三角函数的定义域。
3、三角函数在各个象限的符号。
世上无难事,只怕有心人作业17、18页A组和B组
谢谢大家
再见
