1.2.4 诱导公式(一)课件(28张PPT)
文档属性
| 名称 | 1.2.4 诱导公式(一)课件(28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 312.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-23 09:13:39 | ||
图片预览







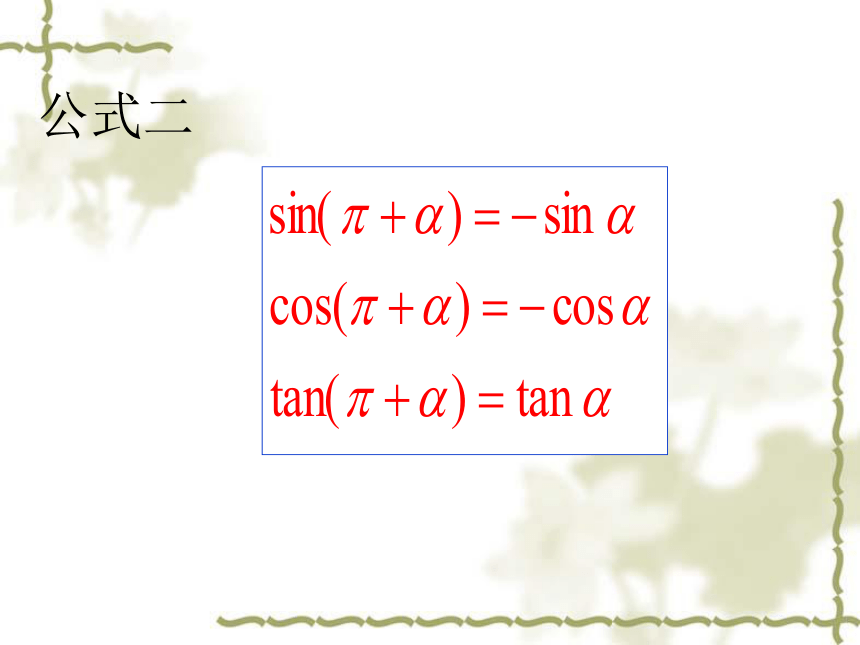
文档简介
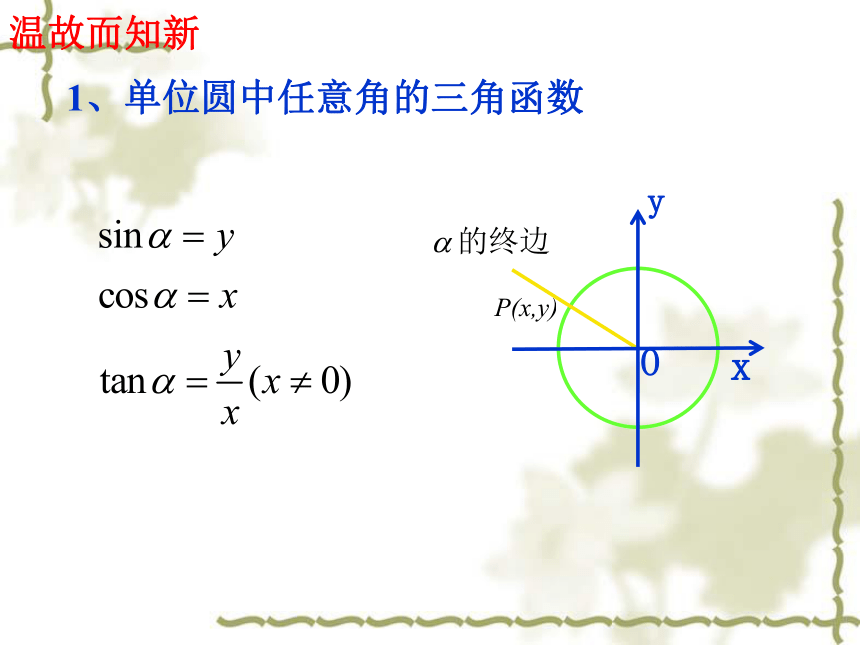
课件28张PPT。1.2.4 三角函数的诱导公式 (第一课时)温故而知新1、单位圆中任意角的三角函数温故而知新2、公式一作用:可以把任意角的三
角函数值,转化为求0到
角的三角函数值。终边相同的角的同一三角函值相等,即练习:求下列三角函数值=?
一个角的终边除了与角 的终边相同之外还有哪些相对特殊的位置关系呢?公式二研究三角函数诱导公式的路线图:
角间关系→对称关系→坐标关系→三角函数值间关系. 设角 的终边与单位圆交于点
P(x,y),则 的终边与单位圆的交点坐标如何?Q(x,-y)公式三3、 与 之间三角函数有什么关系?P(x,y)Q(-x,y)新知探究(三)公式四 公式一二三四如下:均叫做诱导公式 思考:各个公式有什么作用诱导公式公式一,二,三,四都叫做诱导公式。
简化成 “函数名不变,符号看象限”的口诀。
cos225°=? cos225°=cos(180°+45°)=-cos45°= 利用诱导公式一~四,可以把任意角的三角函数转化为锐角三角函数,一般可按下面步骤进行:步骤:负化正 大化小 化到锐角是终了用公式一或公式三用公式一用公式二或公式四思考:已知A,B,C是三角形ABC的三个内角,求证:
cos(2A+B+C)= -cos(A)
tan(A+B)=tan(3π+C)小结:(1)探究三角函数诱导公式的推导过程,理解“函数名不变,符号看象限”。
(2)熟悉将任意角的三角函数转化到锐角三角函数的过程。
(3)熟练掌握三角函数的诱导公式。分层作业数?? 形? ?诗
数形本是相倚依,焉能分作两边飞。
数缺形时少直觉,形少数时难入微。
数形结合百般好,隔离分家万事非。
几何代数统一体,永远联系莫分离。
——华罗庚
再见
角函数值,转化为求0到
角的三角函数值。终边相同的角的同一三角函值相等,即练习:求下列三角函数值=?
一个角的终边除了与角 的终边相同之外还有哪些相对特殊的位置关系呢?公式二研究三角函数诱导公式的路线图:
角间关系→对称关系→坐标关系→三角函数值间关系. 设角 的终边与单位圆交于点
P(x,y),则 的终边与单位圆的交点坐标如何?Q(x,-y)公式三3、 与 之间三角函数有什么关系?P(x,y)Q(-x,y)新知探究(三)公式四 公式一二三四如下:均叫做诱导公式 思考:各个公式有什么作用诱导公式公式一,二,三,四都叫做诱导公式。
简化成 “函数名不变,符号看象限”的口诀。
cos225°=? cos225°=cos(180°+45°)=-cos45°= 利用诱导公式一~四,可以把任意角的三角函数转化为锐角三角函数,一般可按下面步骤进行:步骤:负化正 大化小 化到锐角是终了用公式一或公式三用公式一用公式二或公式四思考:已知A,B,C是三角形ABC的三个内角,求证:
cos(2A+B+C)= -cos(A)
tan(A+B)=tan(3π+C)小结:(1)探究三角函数诱导公式的推导过程,理解“函数名不变,符号看象限”。
(2)熟悉将任意角的三角函数转化到锐角三角函数的过程。
(3)熟练掌握三角函数的诱导公式。分层作业数?? 形? ?诗
数形本是相倚依,焉能分作两边飞。
数缺形时少直觉,形少数时难入微。
数形结合百般好,隔离分家万事非。
几何代数统一体,永远联系莫分离。
——华罗庚
再见
