1.3.1 正弦函数的图象与性质课件(20张PPT)
文档属性
| 名称 | 1.3.1 正弦函数的图象与性质课件(20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-23 09:20:30 | ||
图片预览



文档简介
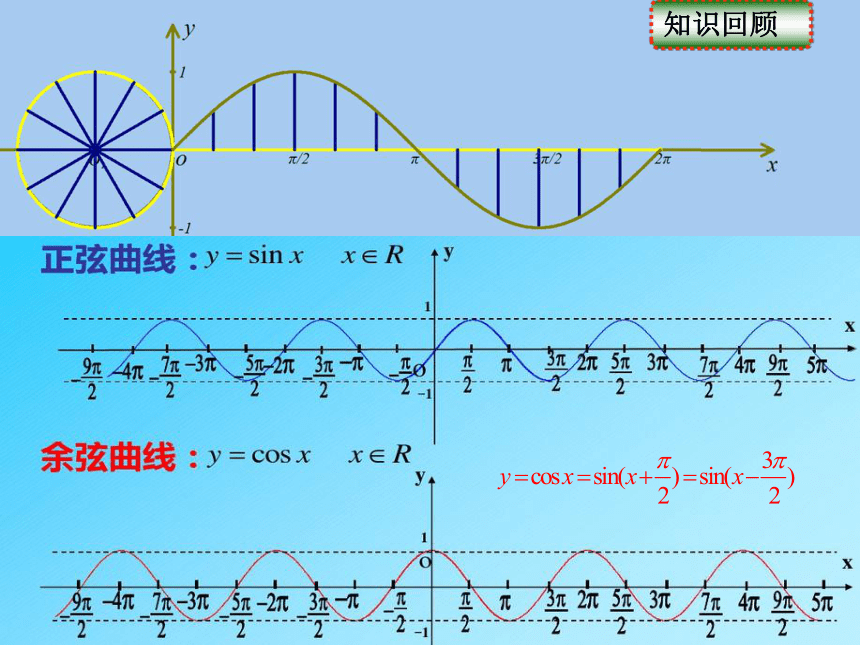
课件20张PPT。正弦函数的性质知识回顾 1.你能判断图中的曲线是正弦曲线还是余弦曲线吗?
(曲线与x轴相邻两交点间的距离为 , x轴与虚线之
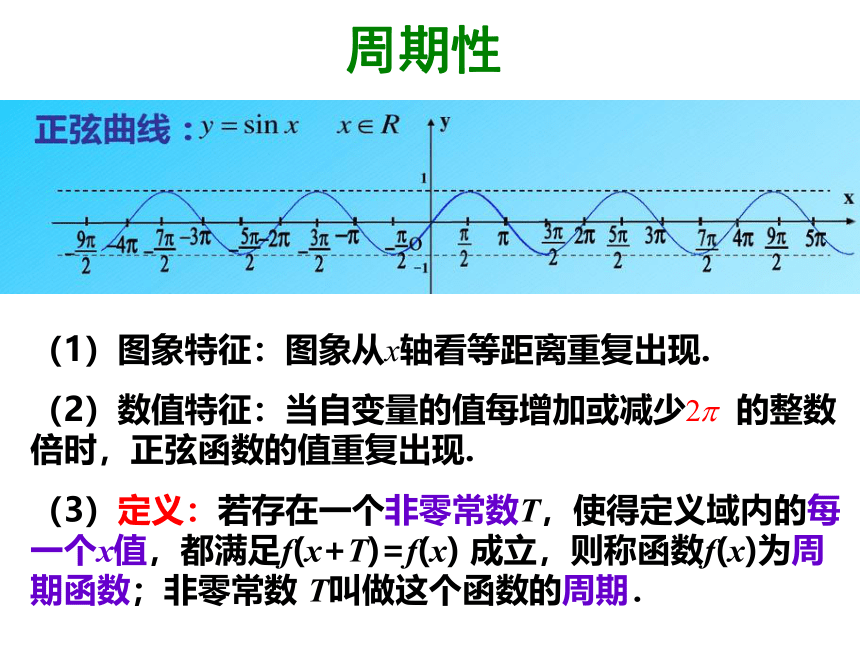
间的距离为单位1.)问题引入2.请你把坐标原点(y轴)补上,使这个图象是正弦函数的图象,坐标原点(y轴)可以补在哪里,说明理由.1.结合正弦函数的图象,探究正弦函数的性质.探索新知定义域、值域、周期性、奇偶性、单调性、对称性.2.对于正弦函数的性质,你能从代数角度加以说明吗?(1)图象特征:图象从x轴看等距离重复出现.
(2)数值特征:当自变量的值每增加或减少 的整数倍时,正弦函数的值重复出现.
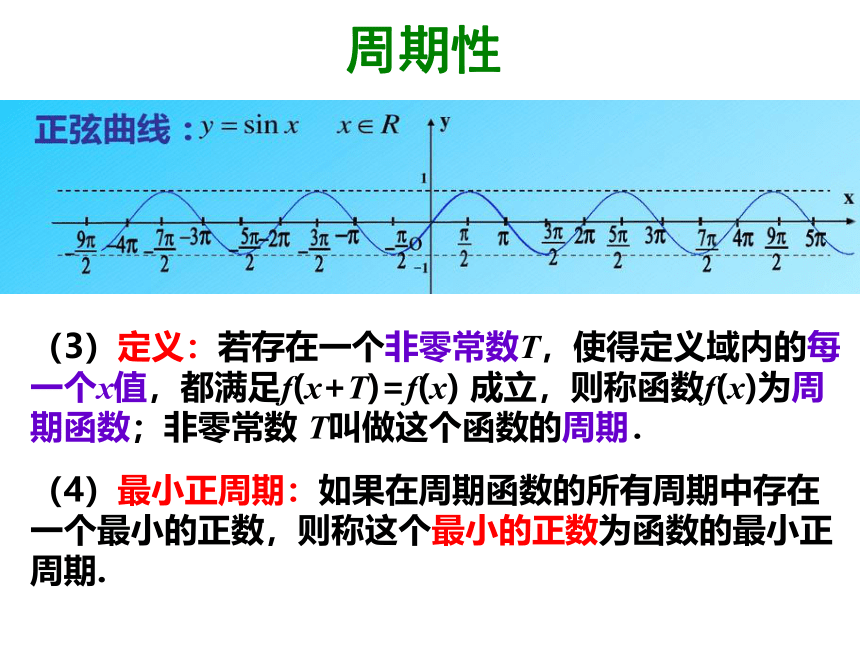
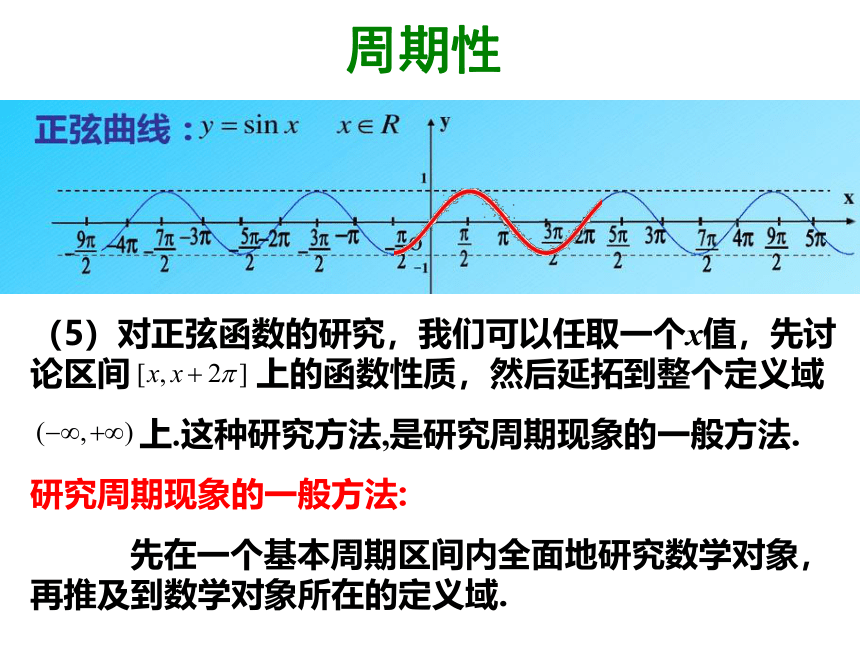
(3)定义:若存在一个非零常数T,使得定义域内的每一个x值,都满足f(x+T)=f(x) 成立,则称函数f(x)为周期函数;非零常数 T叫做这个函数的周期.周期性周期性(3)定义:若存在一个非零常数T,使得定义域内的每一个x值,都满足f(x+T)=f(x) 成立,则称函数f(x)为周期函数;非零常数 T叫做这个函数的周期.(4)最小正周期:如果在周期函数的所有周期中存在一个最小的正数,则称这个最小的正数为函数的最小正周期.周期性(5)对正弦函数的研究,我们可以任取一个x值,先讨论区间 上的函数性质,然后延拓到整个定义域
上.这种研究方法,是研究周期现象的一般方法.
研究周期现象的一般方法:
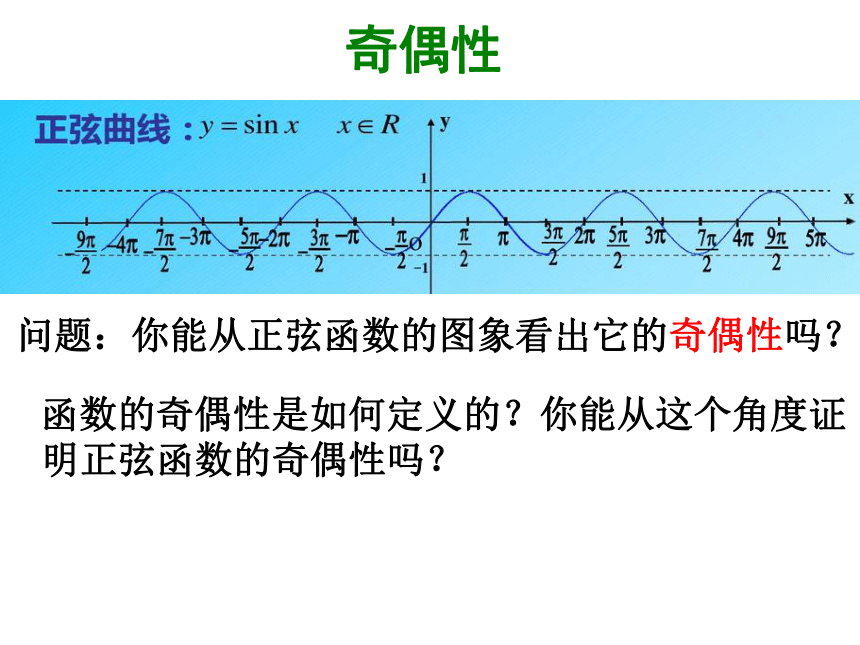
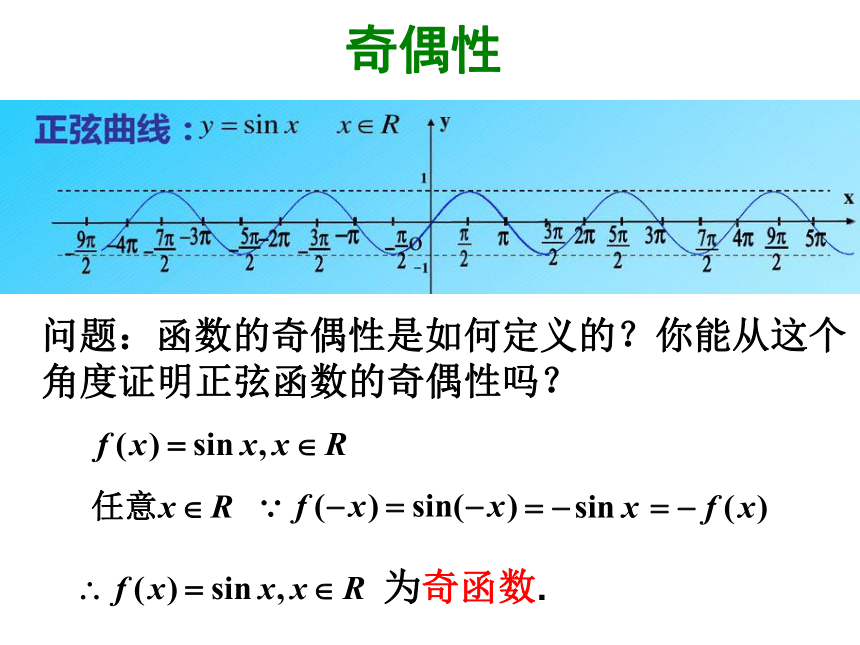
先在一个基本周期区间内全面地研究数学对象,再推及到数学对象所在的定义域.奇偶性问题:你能从正弦函数的图象看出它的奇偶性吗? 函数的奇偶性是如何定义的?你能从这个角度证明正弦函数的奇偶性吗?奇偶性 问题:函数的奇偶性是如何定义的?你能从这个角度证明正弦函数的奇偶性吗?为奇函数.单调性 研究函数的单调性时,基本周期区间未必选取
.
基本周期区间选取的一般原则:
结果的连续性和表达的简洁性
正弦函数的增区间为:其值从-1增大到1;正弦函数的减区间为:其值从1减小到-1.单调性正弦函数的最大值和最小值正弦函数当且仅当x=____________时取得最大
值1,当且仅当x=___________时取得最小值-1.对称性正弦曲线除了关于原点对称外,是否还关于其它的点和直线对称? 正弦曲线关于点(kπ ,0)对称. 正弦曲线关于直线 对称.例1 求使函数y=sin2x,x∈R取得最大值的自变量x的集合,并求最大值.
例2 根据正弦函数的性质,讨论函数
的性质.
例3 不通过求值,指出下列各式大于零还是
小于零.问题探究
2.研究周期问题的一般方法1.正弦函数的性质
3.定性→定量1.一张卷子
2.自己总结余弦函数的性质
再见!
(曲线与x轴相邻两交点间的距离为 , x轴与虚线之
间的距离为单位1.)问题引入2.请你把坐标原点(y轴)补上,使这个图象是正弦函数的图象,坐标原点(y轴)可以补在哪里,说明理由.1.结合正弦函数的图象,探究正弦函数的性质.探索新知定义域、值域、周期性、奇偶性、单调性、对称性.2.对于正弦函数的性质,你能从代数角度加以说明吗?(1)图象特征:图象从x轴看等距离重复出现.
(2)数值特征:当自变量的值每增加或减少 的整数倍时,正弦函数的值重复出现.
(3)定义:若存在一个非零常数T,使得定义域内的每一个x值,都满足f(x+T)=f(x) 成立,则称函数f(x)为周期函数;非零常数 T叫做这个函数的周期.周期性周期性(3)定义:若存在一个非零常数T,使得定义域内的每一个x值,都满足f(x+T)=f(x) 成立,则称函数f(x)为周期函数;非零常数 T叫做这个函数的周期.(4)最小正周期:如果在周期函数的所有周期中存在一个最小的正数,则称这个最小的正数为函数的最小正周期.周期性(5)对正弦函数的研究,我们可以任取一个x值,先讨论区间 上的函数性质,然后延拓到整个定义域
上.这种研究方法,是研究周期现象的一般方法.
研究周期现象的一般方法:
先在一个基本周期区间内全面地研究数学对象,再推及到数学对象所在的定义域.奇偶性问题:你能从正弦函数的图象看出它的奇偶性吗? 函数的奇偶性是如何定义的?你能从这个角度证明正弦函数的奇偶性吗?奇偶性 问题:函数的奇偶性是如何定义的?你能从这个角度证明正弦函数的奇偶性吗?为奇函数.单调性 研究函数的单调性时,基本周期区间未必选取
.
基本周期区间选取的一般原则:
结果的连续性和表达的简洁性
正弦函数的增区间为:其值从-1增大到1;正弦函数的减区间为:其值从1减小到-1.单调性正弦函数的最大值和最小值正弦函数当且仅当x=____________时取得最大
值1,当且仅当x=___________时取得最小值-1.对称性正弦曲线除了关于原点对称外,是否还关于其它的点和直线对称? 正弦曲线关于点(kπ ,0)对称. 正弦曲线关于直线 对称.例1 求使函数y=sin2x,x∈R取得最大值的自变量x的集合,并求最大值.
例2 根据正弦函数的性质,讨论函数
的性质.
例3 不通过求值,指出下列各式大于零还是
小于零.问题探究
2.研究周期问题的一般方法1.正弦函数的性质
3.定性→定量1.一张卷子
2.自己总结余弦函数的性质
再见!
